浅海环境中被动定位方法研究及软件实现
刘亚琴,刘 岩,祝 献
(杭州应用声学研究所,浙江 杭州 310023)
0 引言
目标被动定位是水声学研究的一个重要研究领域,其在海防力量以及海洋强国建设中起着重要作用。现有的定位方法很多,如三元阵被动测距、匹配场定位、匹配模定位、基于波导不变量和基于warping 变换以及模基信号处理水声定位技术等,在利用水声信号进行定位方面已经取得显著成果。然而,涉及具有弹性海底环境时,常规定位方法应用较少,如利用直达波与地声界面波的传播时延差对水中目标进行距离估计[1],利用地震表面波垂直振动与水平振动之间的关系对目标进行方位角估计[2],利用Scholte 波频散特性对距离进行估计[3],利用简正波阶数和地声参数联合起来作为反演参数进行反演,确定地声参数以及声源的距离等[4]。文献[3]利用垂直波阻抗作为测量向量,基于粒子滤波算法,对具有弹性海底环境中的目标声源进行了定位研究。在此基础上,本文将该方法应用于液态Pekeris 波导,形成一套完整的、适合Pekeris 波导以及具有弹性海底的Pekeris 波导环境的定位软件。该定位软件将目标定位过程所涉及的水文环境参数、海底参数以及声源信息、粒子滤波参数进行分区设置,操作简单。
1 垂直波阻抗
对于水平分层介质波导,水中声压、垂直振速及垂直波阻抗可表示为[4-5]:
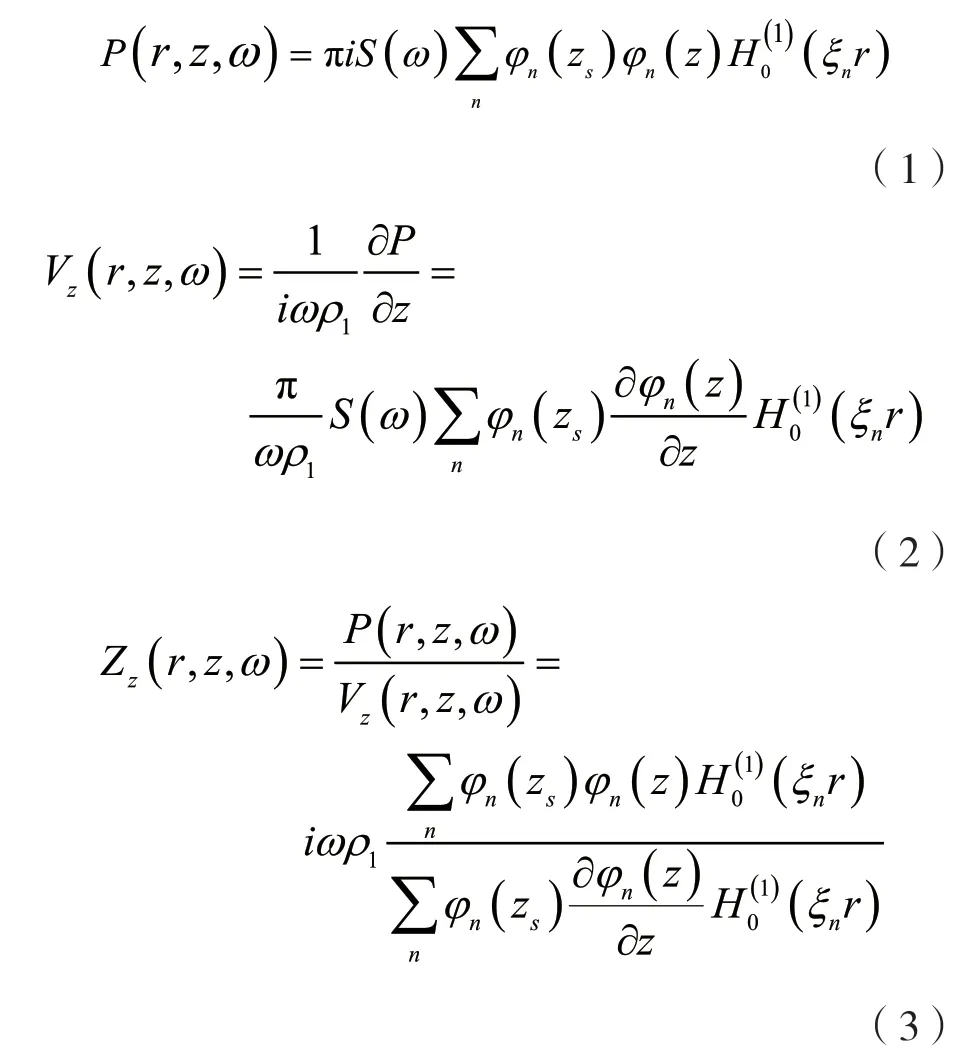
式中:zs表示声源深度,z表示接收深度,r表示接收距离,S(ω)表示声源谱,ω表示角频率,ρ1表示水的密度,φn和ξn分别表示第n阶本征函数和本征值,为第一类第0 阶汉克尔函数,表示本征函数相对于深度z 的导数。
由于垂直波阻抗抵消了声源谱信息,因此,当使用垂直波阻抗进行声源定位,不需要考虑声源频谱信息。这对于被动定位来说是极其有利的。
2 粒子滤波
粒子滤波是一种基于蒙特卡罗方法(Monte Carlo Method)和递推贝叶斯估计的统计滤波方法[6-9]。其核心思想是利用一些离散随机采样点(这些采样点称为粒子)来近似随机变量的概率密度函数,以样本均值代替贝叶斯估计中的积分运算,从而获得状态的估计值。粒子滤波算法在非线性、非高斯系统表现优异,在处理海洋环境这一复杂系统时能够提高估计性能。为了利用粒子滤波进行声源定位,需要构建状态方程和测量方程。其中,状态方程描述状态随时间的变化过程,测量方程描述测量值与状态向量之间的关系。状态方程和测量方程分别为:

式中:状态向量x=[r,zs]T,r和zs分别表示接收器与声源的距离以及声源深度;测量向量y=[Zz1,…,Zzm,…,ZzM]T,Zzm为角频率ωm时垂直波阻抗;wk和vk分别为状态噪声向量和测量噪声向量,对任意i,k满足E{wkwiT}=Qkδki,E{vkviT}=Rkδki,E{vkviT}=0,这里δ(·)是Dirac delta 函数,Qk和Rk分别为k时刻状态噪声和测量噪声的方差矩阵;d(·)为描述测量值与状态向量之间的函数,d(xk)=[d1(x),…,dm(x),…,dM(x)]T,对于液态Pekiers 波导,如图1(a)所示,=β1nm/(Hβ1nm-sinβ1nmHcosβ1nmHb2tanβ1nmHsin2β1nmH),这里,ξnm为角频率ωm时的本征值,H为海深,为水中垂直波数,k1nm=ωm/c1为水中波数,c1为水中声速。
对于具有弹性海底Pekeris 波导,如图1(b)所示,,

图1 环境波导示意图
这里,b=ρ1/ρ2为水中密度与海底密度之比,k2m=ωm/cp、χm=ωm/cs分别为半无限弹性海底纵波、横波波数,cp、cs分别为弹性海底纵波、横波声速,分别为弹性海底纵波、横波垂直波数,。
给出状态方程和测量方程后,定位问题即可用数学模型描述为:已知测量值垂直波阻抗和状态方程、测量方程,找到最优估计参量值(r,zs)即可实现对声源的定位。
假设状态向量的初始概率密度函数Pd(x0)已知,它可以被假设为均匀分布或高斯分布等形式,或用数值技术估算。记Yk=[y1,y2,…,yk]为1 到k时刻测量向量组成的集合,Xk=[x1,x2,…,xk]。从贝叶斯理论角度出发,定位问题关键在于求解状态向量x的后验概率密度Pd(xk|Yk),然后依据最小均方误差或后验概率最大准则估计目标参量最优值。
基于蒙特卡罗积分和序贯重要性采样理论,后验概率可从概率密度分布q(Xk|Yk)采样,得到:
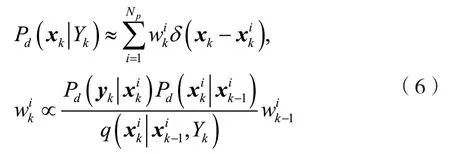

3 定位软件设计实现
定位软件利用接收点处声压、垂直振速时域波形,获取接收点处垂直波阻抗,将接收点处垂直波阻抗作为测量向量,基于粒子滤波算法实现定位。定位软件实现流程如图2 所示。

图2 定位软件实现流程图
其中,接收点处声压时域波形、垂直振速时域波形可表示为:

则,接收点处垂直波阻抗可由声压、垂直振速时域信号获得,如下:

将接收点处垂直波阻抗作为测量值,基于粒子滤波算法,即可完成定位估计。
定位软件界面主要包括参数设置区和结果显示区。参数设置区主要涉及水文环境及工作参数配置区、海底参数设置、声源信号设置以及PF(Particle Filtering)参数设置。参数设置完成后,可通过“时域波形预报”“粒子滤波定位”按钮分别完成声压、振速时域波形预报计算以及定位算法的运行,预报及定位结果在显示区展示。初始界面如图3 所示。

图3 定位软件初始界面
其中,水文环境及工作参数配置区主要设置海深、声速剖面(Sound Speed Profile,SSP)、声源深度、接收深度以及接收距离信息。声速剖面内置良好水文、中等水文以及恶劣水文三种水文条件;海底参数设置主要包括纵波声速、横波声速、纵波衰减、横波衰减以及密度;声源信号设置主要包括信号中心频率、采样频率、信号幅度以及脉冲周期,声源信号形式默认为Hanning 加权的四周期正弦波;PF 参数设置主要包括状态向量初始值、粒子数目以及迭代次数。
所有参数设置完成后,点击“时域波形预报”“粒子滤波定位”按钮,完成时域波形预报与定位结果估计。图4、图5 分别为Pekeris 波导、具有弹性海底的Pekeris 波导环境下的计算结果。从图4、图5可以看出,两种环境下,距离估计曲线、声源深度估计曲线均收敛于设置值附近,表明定位软件能够有效实现目标的被动定位。
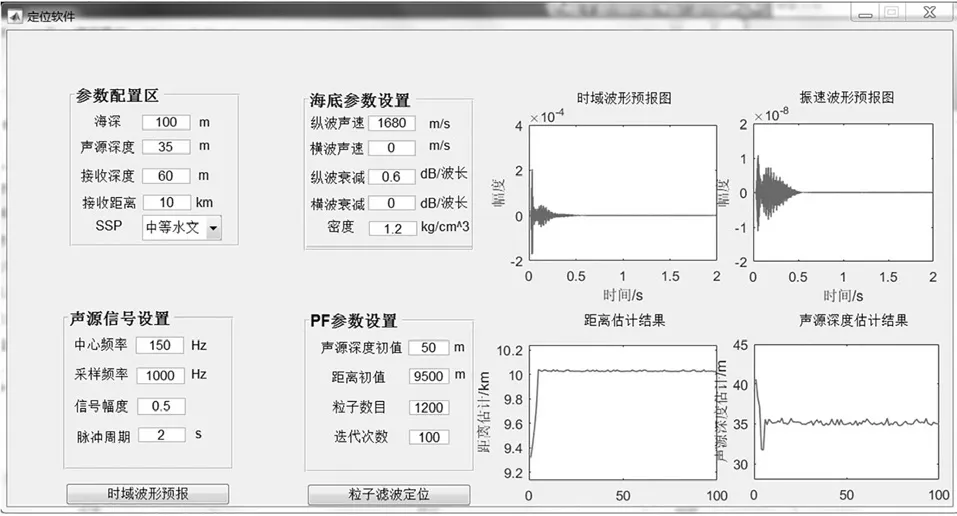
图4 液态Pekeris 波导环境中定位结果

图5 具有弹性海底Pekeris 波导环境中定位结果
4 结语
定位软件基于粒子滤波定位算法,以频率域上垂直波阻抗作为测量向量,构建粒子滤波测量方程,实现浅海环境声源被动定位。定位软件预报了声源信号传播到接收位置处的声压、垂直振速时域波形,在此基础上,获取频率域上垂直波阻抗,基于粒子滤波算法完成距离与声源深度估计。在两种不同波导环境中进行了软件的测试,测试结果表明在两种不同的波导环境中,定位软件计算的距离估计曲线、声源深度估计曲线均收敛于真值附近,表明定位软件能有效完成距离和声源深度的估计。

