耦合双复摆模型的测度同步研究

摘  要：对耦合双摆模型中的测度同步现象进行了研究。该系统是一个哈密顿系统。主要对悬挂在同一横梁下的两个双摆的一个非耗散耦合系统进行分析。通过系统哈密顿量得到系统的运动方程，改变系统耦合强度R（横梁质量与摆上小球质量之比），计算摆角随时间演化图，相空间轨迹图，摆的平均能量图来研究本物理系统到达测度同步现象。当耦合参数达到并且小于临界耦合参数时，从中可以观察到耦合双复摆系统达到了测度同步的状态。该研究完善对于测度同步现象的认知。

关键词：测度同步;哈密顿系统;非耗散系统

中图分类号：TP391.9         文献标识码：A文章编号：2096-4706（2022）02-0081-06

Abstract： The phenomenon of measure synchronization in the coupled double pendulum model is studied. The system is a Hamiltonian system. Mainly analyzes a non-dissipative coupling system of two double pendulums suspended under the same beam. The equation of motion of the system is obtained through the system Hamiltonian， the coupling strength R of the system is changed （the ratio of the mass of the beam to the mass of ball in the pendulum）， the evolution diagram of the pendulum angle with time， the phase space trajectory diagram， and the average energy diagram of the pendulum are calculated， the synchronization phenomenon of arrival measure of this physical system is studied. When the coupling parameter reaches and is smaller than the critical coupling parameter， it can be observed that the coupled double compound pendulum system reaches the state of measurement synchronization. This study refines our understanding of the phenomenon of measure synchronization.

Keywords： measure synchronization; Hamiltonian system; non-dissipative system

0  引  言

人类定义自然界中将至少在多个客体系统间存在的相对的具有一致性的运动关系为同步现象，我们可以在自然界的各个方面中发现同步现象的存在。同步现象是由荷兰物理学家Huygens无意间发现的。研究同步过程中大多数讨论的是在耗散系统中，而对于保守系统，由于Liouville定理的限制，保守系统的相空间守恒不会存在吸引子导致相空间塌缩，所以保守系统中不会出现耗散系统中出现的同步现象。Hampton 和 Zanette等人在二维映像系统中发现了测度同步现象，这种现象发生在保守系统中，保守系统中的测度同步存在系统间的耦合作用[1]。Vincent通过对耦合Duffing 哈密顿系统集体行为的观察发现在准周期和混沌态中存在着测度同步现象，并且提出了部分测度同步的概念[2]。陈绍英等提出了测度同步的数值判定方法。其基本思想是：由保守系统的性质和由测度同步的含义可知，在投影平面上每一系统演化的相空间中任一相点的任意小的邻域内总能找到另一个系统的运动轨迹[3]。田静等在双组分玻色-约瑟夫逊结中发现了测度同步现象以及非局域化测度同步现象，并利用Poincaré截面分析方法对测度同步的发生机理给出了一般性的解释[4]。Gupta等研究了非线性耦合哈密顿系统中的测度同步现象，通过振荡器频率随耦合强度的变化，详细描述了测度同步的转变过程，并找到合适的序参量，准确识别系统中测度同步的转变过程[5]。

本文主要是对于非耗散耦合哈密顿双复摆中的测度同步现象的研究，在该物理系统中我们将两个复摆悬挂在一个刚性横梁上，并对该物理模型进行动力学分析，计算该系统的哈密顿量得到系统的运动方程。通过改变系统的耦合参数R，我们能够得到该系统的摆角随时间演化图，相空间轨迹图，复摆的平均能量图。通过对图像的分析对于系统的测度同步现象的变化过程，最后总结得到的相关现象。

1  模型

本文所研究的非耗散耦合复摆系统是一个将N个复摆悬挂于一个刚性横梁上。横梁的质量为M，并且该横梁可以沿着水平方向移动，水平方向上的位移由x表示，这里的每个双摆由两个摆以及固定在摆的底端上的质量组成，如图1所示。

第i个上摆和第i个下摆的长度由li1和li2（i=1，2，3，…，N）表示。同样的，每个摆的质量都集中于摆的底端，第i个上摆和第i个下摆的质量由mi1和mi2（i=1，2，3，…，N）表示。在本文中为了便于计算，所以我们使摆具有相同的长度li1=li2=l，以及質量mi1=mi2=m。每个摆的摆角可由θi1（上摆）θi2（下摆）表示。假设系统的阻尼系数很小，可以忽略系统的耗散。因此我们所分析的系统是一个非耗散耦合双复摆系统。为了简化模型，我们考虑有两个复摆悬挂在横梁上，即N=2。

那么我们根据系统的模型可以写出系统的哈密顿量：

θi1和θi2是双摆的位移角度，重力加速度g。利用拉格朗日方程计算系统的运动方程：

通过进行如下变换将系统无量纲化。将公共横梁的无量纲位置定义为y=x/l，无量纲时间定义为T=ω0t，耦合摆角的角频率为。得到如下运动方程：

在上述方程中我们引入一个自由参数（横梁与摆质量之比）为系统的耦合参数。

2  数值模拟

将系统的运动方程采用四阶龙格库塔法进行计算。并且只考虑摆质量m=1摆长l=0.2485，摆的固有频率ω0=2π，系统的初始条件设置为：θ11（0）=0.145;θ12（0）=0.205;θ21（0）=-0.05;θ22（0）=-0.07;（0）=0;（0）=0; （0）=0;（0）=0。

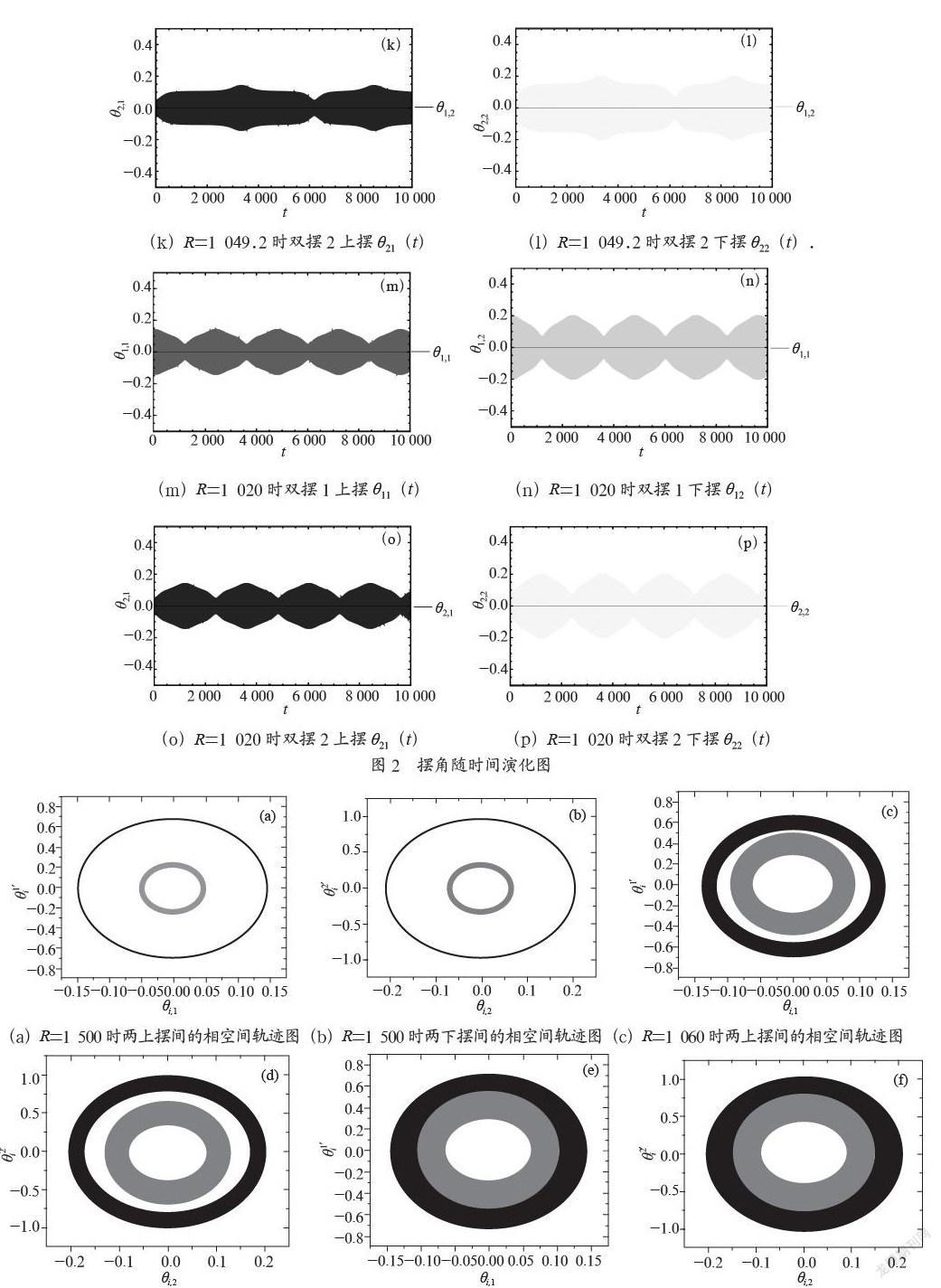
图2为θ11（t），θ12（t），θ21（t），θ22（t）在不同R值下随时间演化情况，（a）、（e）、（i）、（m）代表θ11（t），（b）、（f）、（j）、（n）代表θ12（t），（c）、（g）、（k）、（o）代表θ21（t），（d）、（h）、（l）、（p）代表θ22（t），每一组对应一个R值，R=1 500/1 060/1 049.2/1 020。不同的两个摆角θ11（t），θ21（t）以及θ12（t），θ22（t）的随时间演化图揭示了大时间尺度上的连贯动力学迹象。当R=1 500（图2（a）、（b）、（c）、（d））时θ11（t）的振幅始终大于θ21（t）同样的θ12（t）的振幅始终大于θ22（t），并且振幅都随时间变化而变化。当R=1 060（图2（e）、（f）、（g）、（h））时，θ11（t）的振幅始终大于θ21（t）同样的θ12（t）的振幅始终大于θ22（t），但与R=1 500时不同，振幅随时间变化的现象更加显著。当R=1 049.2（图2（i）、（j）、（k）、（l））时，摆的随时间演化图突然发生动态变化，表现出了明显的相干动力学，即θ11（t）与θ21（t）的最大振幅相同，θ11（t）与θ21（t）的振幅峰值变化存在最大相位差π同时θ12（t）与θ22（t）的最大振幅相同，θ12（t）与θ22（t）的振幅峰值变化存在最大相位差π。当我们继续减小R=1 020（图2（m）、（n）、（o）、（p））时系统中摆的相干动力学现象更为显著。至此我们发现当耦合系数小于某个值Rc时，系统就会出现这种一致行为。如果我们观察和，和在不同R值下的时间演变，也会出现类似的特征。然而，如果我们放大时间进行演化，尽管在表观相干动力学行为的背后已经实现了弱相位同步，但是我们将看不到完整的同步跡象。所以我们发现这个阈值Rc=1 049.2。

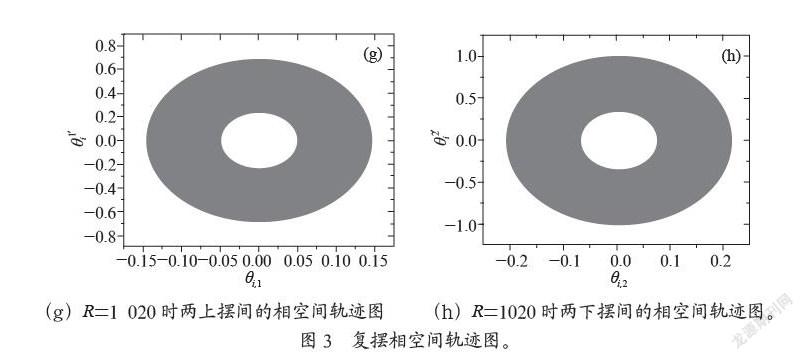
为了进一步探索相干动力学，我们在相空间中绘制了耦合复摆系统的相空间轨迹图。

如图3所示，我们在相空间中分别绘制了和（i=1，2）的相空间域，图中黑色部分代表i=1，红色部分代表i=2。图3中（a）与（b）显示了R=1 500时复摆的相空间域。图3中（c）与（d）表示了R=1 060时的相空间域。图3中的（e）和（f）代表了R=1 049.3时的相空间域。图3中（g）和（h）代表了R=1 049.2时的相空间域。对于近似非耦合的情况，如R=1 500时我们可以观察到在相空间中两条不同的曲线，这代表了相空间的周期运动。当R减小到1 060时由于共梁引入的耦合效应，可以观察到两个摆在相空间上的两个相空间域。随着R的减小我们可以观察到两边的相空间域逐渐接近至R=1 049.3可以看到内相空间域的外边界逐渐与外相空间的内边界的间隔已经非常接近但还未发生突变。当耦合参数达到临界阈值RC=1 049.2时（如图3（g）和（h）所示），相空间域发生了突变，两个相空间域达到了完全重叠的状态。综上所述，在耦合参数达到阈值后和的相空间域完全重叠，这个状态被称为测度同步现象。因此我们可以得出，在非耗散耦合共梁双复摆系统中存在测度同步现象。

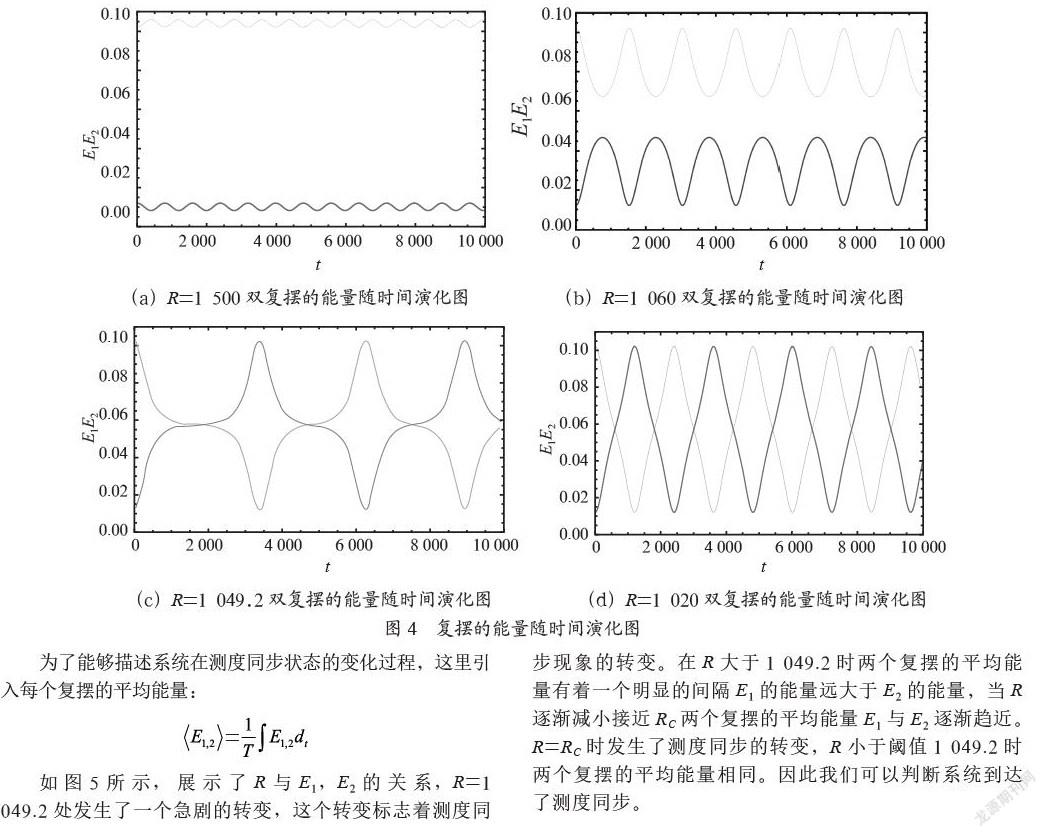
如图4所示，为了更加准确的耦合复摆系统的测度同步现象的相变行为我们讨论了非耗散耦合复摆系统的复摆能量随时间演化。图4（a）～（d）显示了每个复摆的能量随时间演化情况。图中绿色线条表示第一个摆l11+l12，红色线条表示第二个摆l21+l22。图4（a） ～（d）分别对应不同耦合系数R=1 500/1 060/1 049.2/1 020的图像。当R>RC时系统未达到测度同步转变之前，如图4（a）中R=1 500时，E1与E2完全不重叠，两个复摆的能量有各自的能量变化行为。随着R的减小当R=1 060时E1与E2完全不重叠但已经发生了能量曲线互相接近的表现，初始能量高的下边界逐渐接近初始能量低的摆的上边界。当继续减小R达到临界耦合强度RC=1049.2时，在达到临界耦合参数RC后如图4（c），E1与E2有着完全相同的能量变化范围，并且有着相位差π。继续减小R=1020后如图4（d），E1与E2保持着完全相同的能量变化范围并且存在相位差π。这种现象说明两个双摆达到了全部的测度同步。

为了能够描述系统在测度同步状态的变化过程，这里引入每个复摆的平均能量：

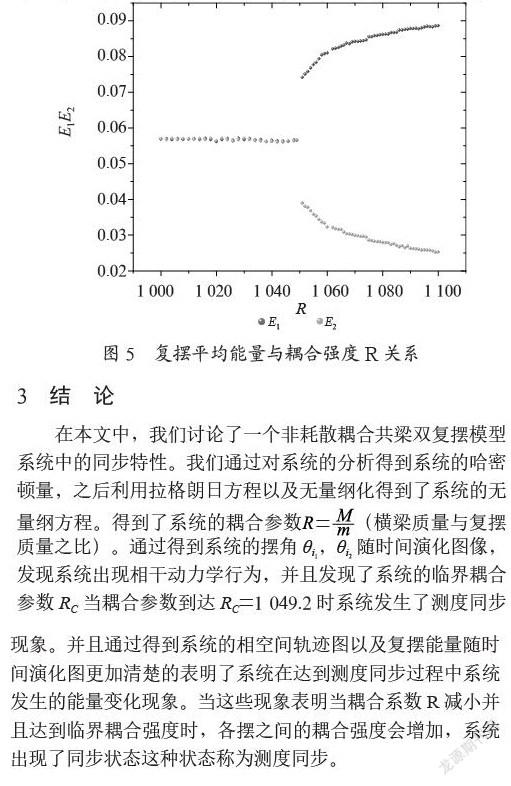
如图5所示，展示了R与E1，E2的关系，R=1 049.2处发生了一个急剧的转变，这个转变标志着测度同步现象的转变。在R大于1 049.2时两个复摆的平均能量有着一个明显的间隔E1的能量远大于E2的能量，当R逐渐减小接近RC两个复摆的平均能量E1与E2逐渐趋近。R=RC时发生了测度同步的转变，R小于阈值1 049.2时两个复摆的平均能量相同。因此我们可以判断系统到达了测度同步。

3  结  论

在本文中，我们讨论了一个非耗散耦合共梁双复摆模型系统中的同步特性。我们通过对系统的分析得到系统的哈密顿量，之后利用拉格朗日方程以及无量纲化得到了系统的无量纲方程。得到了系统的耦合参数（横梁质量与复摆质量之比）。通过得到系统的摆角θi1，θi2随时间演化图像，发现系统出现相干动力学行为，并且发现了系统的临界耦合参数RC当耦合参数到达RC=1 049.2时系统发生了测度同步现象。并且通过得到系统的相空间轨迹图以及复摆能量随时间演化图更加清楚的表明了系统在达到测度同步过程中系统发生的能量变化现象。当这些现象表明当耦合系数R减小并且达到临界耦合强度时，各摆之间的耦合强度会增加，系统出现了同步状态这种状态称为测度同步。

参考文献：

[1] ALAN H，ZANETTE D H. Measure Synchronization in Coupled Hamiltonian Systems [J].Physical Review Letters，1999，83（11）：2179-2182

[2] VINCENT U E. Measure synchronization in coupled Duffing Hamiltonian systems [J].New Journal of Physics，2009（7）：1-9.

[3] 陈绍英，许海波，王光瑞，等.耦合哈密顿系统中测度同步的研究 [J].物理学报，2004（12）：4098-4110.

[4] TIAN J，QIU H B，WANG G F，et al. Measure synchronization in a two-species bosonic Josephson junction [J/OL].Physical Review E，2013，88（3）：032906[2021-09-25].https：//journals.aps.org/pre/abstract/10.1103/PhysRevE.88.032906.

[5] GUPTA S，DE S，JANAKI M S，et al. Exploring the route to measure synchronization in non-linearly coupled Hamiltonian systems [J/OL].Chaos：An Interdisciplinary Journal of Nonlinear Science，2017，27（11）：113103[2021-09-25].https：//aip.scitation.org/doi/10.1063/1.4996814.

作者简介：孟乐言（1996.08—），男，汉族，陕西铜川人，硕士研究生在读，研究方向：非线性动力学。