室内受限空间中掺氢天然气爆炸模拟

陈卓， 李敬法， 宇波

(1.中核控制系统工程有限公司， 北京 102401； 2.北京石油化工学院机械工程学院并氢能研究中心， 北京 102617)

氢能具有来源广、燃烧产物无污染等优点，被誉为21世纪最有发展前景的清洁能源。国家“十四五”规划已将发展氢能作为重要的能源战略，而氢的输送是氢能产业战略发展的重要方向[1]。将氢气掺入天然气管道或管网中与天然气混输，是实现氢气高效输送的一种可行方式[2]。目前已开展的掺氢天然气输送示范项目多采用现有的天然气管道或管网输送，输送过程中管道腐蚀、材料老化、外力破坏等因素可能导致掺氢天然气泄漏。此外，氢气和天然气均为易燃易爆气体，其泄漏后与空气混合形成可燃气体，遇明火极易发生爆炸，造成严重事故后果。因此，开展掺氢天然气泄漏爆炸事故特征和演化规律研究具有重要现实意义。

目前氢气和天然气爆炸事故的研究手段主要有实验方法和数值模拟。Li等[3]研究了氢气-空气混合物和氢气-甲烷-空气混合物的无限制管道通风爆炸，通过实验获得了爆炸室内的爆炸压力，结果表明对于无限制氢气-甲烷爆炸，随着甲烷量的增加，最大爆炸压力和最大压力增长速率均逐渐减小。Zhang等[4]为了探讨掺氢天然气输送的可行性，分别以100% CH4、90% CH4+10% H2、80% CH4+20% H2(均为体积分数)为燃料对综合管廊气室内的爆炸进行了实验研究，发现随着掺氢比的增加，相同体积的气云超压增大，10%H2和20%H2的超压分别增大16%和32%。田莉[5]实验研究了受限空间内不同氢气含量下预混气体的爆炸特性，结果表明氢气含量越高，预混气体爆炸的威力也越大。Kim等[6]模拟了不同压力和泄漏口尺寸条件下，加氢站发生氢气泄漏时的爆炸情况，分析了爆炸压力分布特征和爆炸方向性。Zhang等[7]分析了不同体积分数的氢气、丙烷、甲烷与空气混合后在有内置障碍物约束的空间内的爆炸特性，结果表明在其他条件相同时氢气和空气的混合气体爆炸具有较高的峰值压力，但3种气体爆炸时不同位置的爆炸温度几乎无差异。姜楠等[8]模拟了氢气管道发生泄漏后的爆炸事故，发现爆炸火焰传播造成的气体流动是产生爆炸超压的根本原因。刘自亮等[9]利用FLACS软件研究了埋地输氢管道泄漏爆炸事故后果，分析了不同泄漏孔径、泄漏时长、输氢压力以及环境风速对爆炸的影响，发现泄漏孔径和输氢压力越大，爆炸产生的最大超压和危险区域也越大。Zhang等[10]对氢气爆炸过程进行了模拟研究，发现当氢气体积分数为30%时爆炸压力和压力增长速率在1.01×105Pa时达到最大值，随着初始压力的增大，爆炸压力和压力增长速率逐渐增大。

目前单独针对氢气或天然气爆炸的研究较多[11-15]，但针对掺氢天然气混合气体爆炸的研究很少。尽管掺氢天然气爆炸与天然气爆炸有着相似之处，但受掺入氢气的影响，掺氢天然气爆炸事故规律与天然气存在一定差异，需进一步开展更深入的研究。现针对室内受限空间中掺氢天然气爆炸进行模拟研究，以期为室内掺氢天然气安全利用提供理论指导。

1 掺氢天然气爆炸数理模型

掺氢天然气混合气体爆炸的完整数学描述包括连续性方程、动量方程、能量方程、湍流方程、组分输运方程和燃烧方程。

(1)连续性方程：

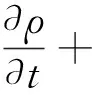
(1)

式(1)中：ρ为掺氢天然气混合气体的密度，kg/m3；t为时间，s；u为速度，m/s。

(2)动量方程：

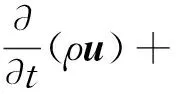
(2)

式(2)中：p为压力，Pa；τeff为有效张量应力；g为重力加速度，m/s2。

(3)能量方程：

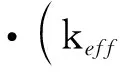
(3)

式(3)中：E为气体微团总能；keff为有效导热系数，W/(m·K)；T为温度，K；hj为组分j的焓；Jj为组分j的扩散通量；j为掺氢天然气中组分的数目。

(4)标准k-ε模型：

(4)

(5)

式中：k为湍动能；ε湍动能耗散率；v为运动黏度；μ为动力黏度；μt为湍流黏度，Pa·s；Gk为平均速度梯度引起的湍流动能；Gb为浮力引起的湍流动能；C1、C2、C1ε、C3ε为常数；σk、σε为湍流普朗特数。

(5)组分输运模型：

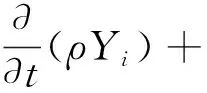
(6)

式(6)中：Yi为组分i的质量分数，%；Ji为组分i的质量扩散通量，kg/(m2·s)。

(6)通用燃烧方程:

CaHbOcSd+3.76yO2+yN2=n1CO+n2CO2+

n3H2O(g)+n4N2+n5O2+n6SO2+

n7CaHbOcSd+Qf

(7)

式(7)中：a、b、c、d分别为燃料气体分子式中所含有的碳、氢、氧、硫原子个数；n1、n2、n3、n4、n5、n6分别为气体燃烧后生成物中CO、CO2、H2O、N2、O2、SO2物质的量；n7为剩余可燃气体物质的量；Qf为热量。

2 掺氢天然气爆炸事故模拟

2.1 物理模型简介

掺氢天然气爆炸事故按照发生场景可简单分为室内掺氢天然气爆炸和室外掺氢天然气爆炸。由于一般情况下室内受限空间中掺氢天然气爆炸事故对人员的生命威胁更严重，因此仅针对室内受限空间中掺氢天然气爆炸事故进行模拟研究。如图1所示，选取的室内受限空间物理模型为长4 m、宽3 m、高3 m且带门窗的长方体空间。为简化模拟计算，假设初始时刻空间内各处均匀分布着掺氢天然气。

图1 掺氢天然气爆炸事故物理模型Fig.1 Physical model of explosion accident of hydrogen-enriched natural gas

2.2 算例条件设置

采用爆炸模拟软件FLACS对掺氢天然气爆炸进行研究。采用六面体网格划分计算区域，网格总数为36 000，单个网格为边长0.1 m的六面体。模拟中考虑掺氢比、打火点位置、计算区域是否开放和燃烧程度4种因素的影响，算例条件详细设置如表1所示。其中，算例0～算例4主要考察掺氢比的影响，算例2、算例5、算例6主要考察打火点位置的影响，算例2、算例7主要考察计算区域是否开放的影响，算例2、算例8～算例10主要考察燃烧程度的影响。本文研究中燃烧程度在软件中通过当量比(equivalence ratio, ER)表征，ER>1时表示可燃气云中氧气含量小于理论上燃烧所需要的氧气含量，即氧气量不足；ER=1时表示可燃气云中氧气含量等于理论上燃烧所需要的氧气含量，此时燃烧最为剧烈；ER<1时表示可燃气云中氧气含量大于理论上燃烧所需要的氧气含量，即氧气量过剩。

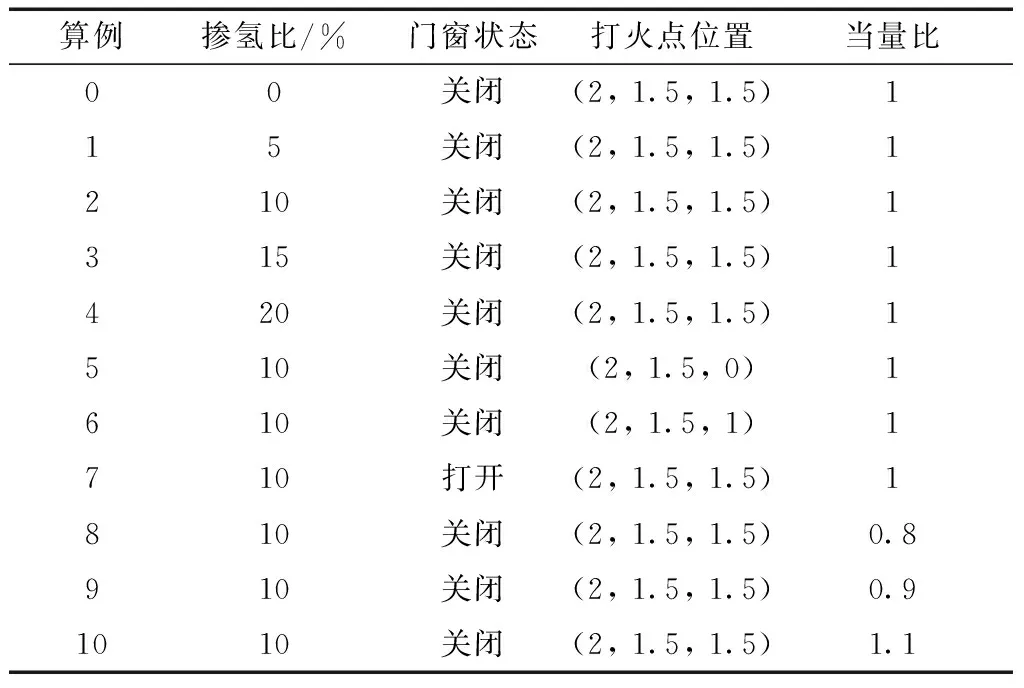
表1 掺氢天然气爆炸事故不同算例参数设置Table 1 Parameter setting for different explosion accident cases of hydrogen-enriched natural gas

2.3 软件初始参数设置

以算例2为例，简要介绍FLACS软件中的模拟参数设置。模拟过程中设置初始温度为293 K，初始压力为0.1 MPa，掺氢天然气均匀充满整个计算区域，气体成分中设置甲烷为9，氢气为1，即掺氢比初始值为10%，设置ER初始值为1.0，即此时为完全燃烧情况。同时设置打火初始位置位于气云中心，其坐标为(2, 1.5, 1.5)，打火开始时间为0 s，具体参数设置如表2所示。为定量分析爆炸的模拟结果，便于揭示掺氢天然气爆炸规律，在计算区域中添加三个监测点(M1、M2、M3)，坐标分别为(2, 1.5, 1.5)、(2, 1.5, 0)、(0, 0, 0)，各监测点位置如图2所示。

表2 FLACS软件中的模拟参数设置Table 2 Simulation parameter setting in FLACS software

图2 监测点位置示意图Fig.2 The location of monitoring points

3 结果分析

3.1 掺氢天然气爆炸事故非稳态过程分析

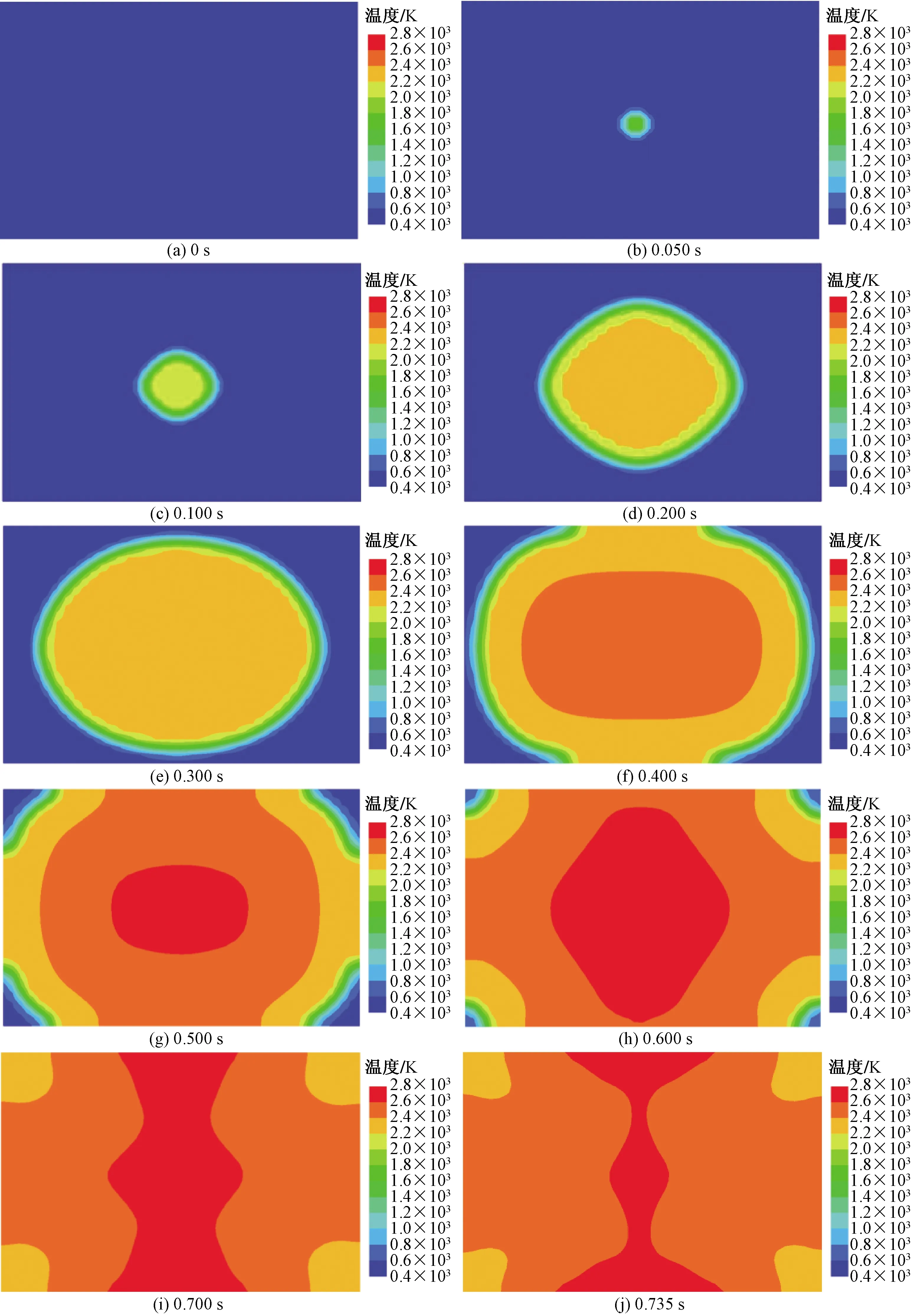
图3 算例2不同爆炸时刻的温度场分布Fig.3 Temperature field distribution of case 2 at different explosion time

首先以算例2为例，分析室内掺氢天然气爆炸事故过程中的温度变化过程。图3给出了算例2不同爆炸时刻1.5 m高度(中心截面)处的X-Y二维温度云图。可以看到，0 s时(爆炸还未发生)整个计算区域内的温度为初始温度293 K，而0.05 s时(爆炸初期阶段)在计算区域中心，即打火点附近温度明显升高，此时温度云图为规则对称的近似圆形。由此可推断出0.05 s时刻在一个以打火点为球心的近似球状空间内温度明显升高。随着爆炸的进行，该近似球形升温区域的半径越来越大，球形内部的爆炸温度也越来越高，到0.2 s时内部的温度已达到近2 500 K。在球形升温区域Y方向的直径快达到计算区域的宽度时，由于受到壁面的阻碍，不再继续增长。而球形升温区域X方向上并没有受到壁面的阻碍，于是0.3 s时二维平面温度云图为椭圆形，可推断此时三维空间内的温度云图近似椭球形。随着爆炸的进行，计算区域内的温度都大幅度上升，最高温度可达到约2 902 K。综上可知，整个爆炸过程短暂且急促，并且释放出大量能量使得计算区域内的温度急剧升高，在不到1 s时间内计算区域内的平均温度由293 K升高到2 863 K，增加了2 570 K。

3.2 掺氢比对掺氢天然气爆炸事故的影响

掺氢比是掺氢天然气的一项重要参数，对比算例0～算例4的结果可分析出掺氢比对掺氢天然气爆炸过程中温度和压力的影响。图4(a)给出了算例0～算例4不同掺氢比下监测点2处的温度在爆炸过程中的变化。可以看出，对于监测点2，随着掺氢比的增加，爆炸发生时间逐渐提前。这是因为氢气在空气中的最小点火能量为0.017 mJ，远小于甲烷在空气中的最小点火能量0.274 mJ。随着掺氢比的增加，掺氢天然气混合气体的最小点火能量逐渐减小，导致爆炸发生时间提前。但在这5种掺氢比情况下，爆炸温度随爆炸时间的变化趋势基本一致。

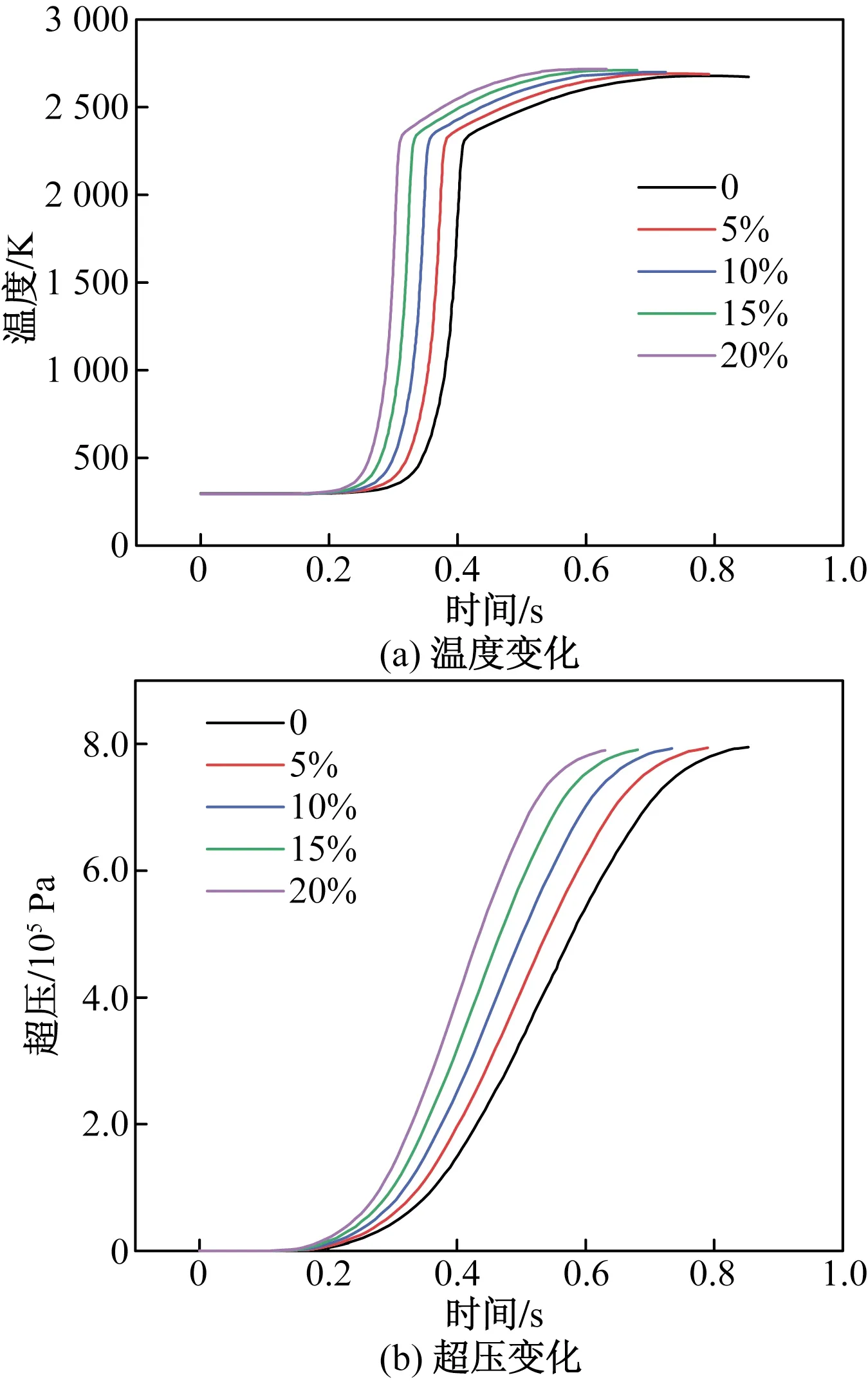
图4 不同掺氢比下监测点2处的温度和超压变化Fig.4 Variation of temperature and overpressure at monitoring point 2 under different hydrogen blending ratios

图4(b)给出了不同掺氢比下监测点2处的超压在爆炸过程中的变化。可以观察到，与温度变化趋势类似，不同掺氢比情况下超压随爆炸时间的变化趋势基本一致，区别在于爆炸发生时间不同。随着掺氢比的增加，爆炸发生时间逐渐提前，同时爆炸过程中所达到的最大超压基本不变，并且都达到了7.6×105Pa以上。表3和表4分别给出了不同爆炸冲击波超压对人体的伤害情况和对建筑物的破坏情况。对比表可以发现，5种掺氢比情况下的爆炸威力都很大，能够造成严重的破坏。对人体能够达到严重伤害程度，可能会导致心肌、脱臼撕裂的情况，同时能使建筑物的砖墙倒塌。

表3 爆炸冲击波对人体的伤害Table 3 Damage of blast wave to human body

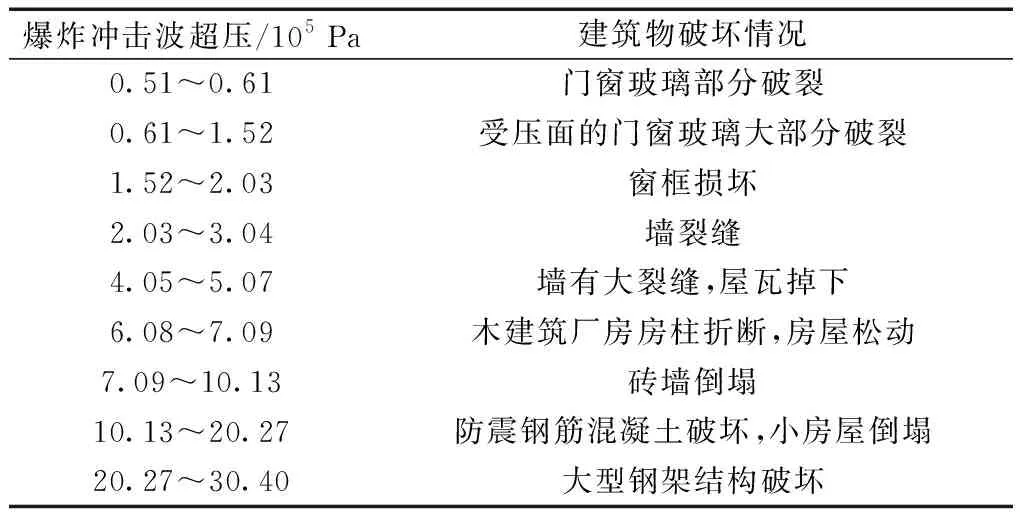
表4 爆炸冲击波对建筑物的破坏Table 4 Damage of blast wave to buildings

3.3 打火点位置对掺氢天然气爆炸事故的影响

通过算例2、算例5、算例6的模拟结果分析打火点位置对掺氢天然气爆炸事故的影响。图5(a)给出了3种不同打火点高度情况下爆炸过程中监测点1处的温度变化。从中可以看到，三条温度变化曲线相似，不同之处在于温度开始剧烈上升的时间。打火点高度距离监测点1越近，监测点1处温度剧烈上升的时间越早。按照监测点1处温度开始剧烈上升的时间顺序排列，依次是算例2、算例6、算例5。

图5(b)给出了3种不同打火点高度情况下爆炸过程中监测点1处的超压变化。同温度变化曲线一样，三条超压曲线随爆炸时间的变化趋势基本一致，区别主要在于超压开始剧烈上升的时间。打火点位置距离监测点1越近，超压开始剧烈上升的时间越早，在监测点1处，算例5比算例2温度开始变化的时间早0.2 s左右。这是因为爆炸是以波的形式传播的，距离爆炸中心(打火点)越近，爆炸波到达此处所需要的时间越小，因此此处的温度和超压开始剧烈上升的时间越早。

图5 不同打火点高度情况下监测点1处的温度和 超压变化Fig.5 Variation of temperature and overpressure at monitoring point 1 under different ignition point heights

3.4 计算区域是否开放对掺氢天然气爆炸事故的影响

算例7中物理模型的门窗处于开启状态，物理模型从封闭空间变成与大气连通的开放空间。门窗状态对掺氢天然气爆炸事故后果的影响很大。图6(a)给出了门窗处于开启和关闭两种状态下监测点1处的温度随爆炸时间的变化。可以看出，打开门窗之后爆炸发生时间要晚于门窗封闭的情况，并且爆炸初期温度上升趋势也比门窗封闭的情况平缓，爆炸结束后温度趋于平衡的时间也比门窗封闭情况要早，打开门窗后爆炸用时远小于门窗封闭情况下的掺氢天然气爆炸事故。同时门窗关闭情况下监测点1处爆炸过程中所达到的最大温度为2 777.6 K，而打开门窗后监测点1处在爆炸过程中所达到的最大温度为2 234.2 K，比前者降低了543.4 K，这是因为门窗打开后，爆炸波开始向外界大气传播，热量被传递到外界大气中。

图6(b)给出了门窗开启和关闭两种情况下监测点1处的超压变化。从中可看到，与门窗关闭情况相比，门窗开启时超压变化很小。这是因为开启门窗后，爆炸区域与大气连通，发生爆炸时压力波从门窗瞬间传到大气中，因此监测点1处所测得的超压变化很小。

3.5 燃烧程度对掺氢天然气爆炸事故的影响

可燃气云燃烧是否充分对爆炸威力具有较大影响。下面通过算例2、算例8～算例10的模拟结果分析燃烧程度对掺氢天然气爆炸事故的影响。图7(a)给出了4种不同燃烧程度情况下监测点1处的温度变化。可发现4种情况下的温度变化趋势基本一致，但爆炸所产生的最大温度随ER的增大逐渐增大，ER=0.8时最大爆炸温度为2 501.5 K，而ER=1.1时最大爆炸温度达到了2 810.2 K，比前者上升了308.7 K。还可发现，随着ER的增大，爆炸发生的时间逐渐缩短，ER=1.1时的爆炸时间比ER=0.8时的爆炸时间缩短约0.4 s。

图6 门窗状态不同情况下监测点1处的温度和 超压变化Fig.6 Variation of temperature and overpressure at monitoring point 1 under different conditions of doors and windows

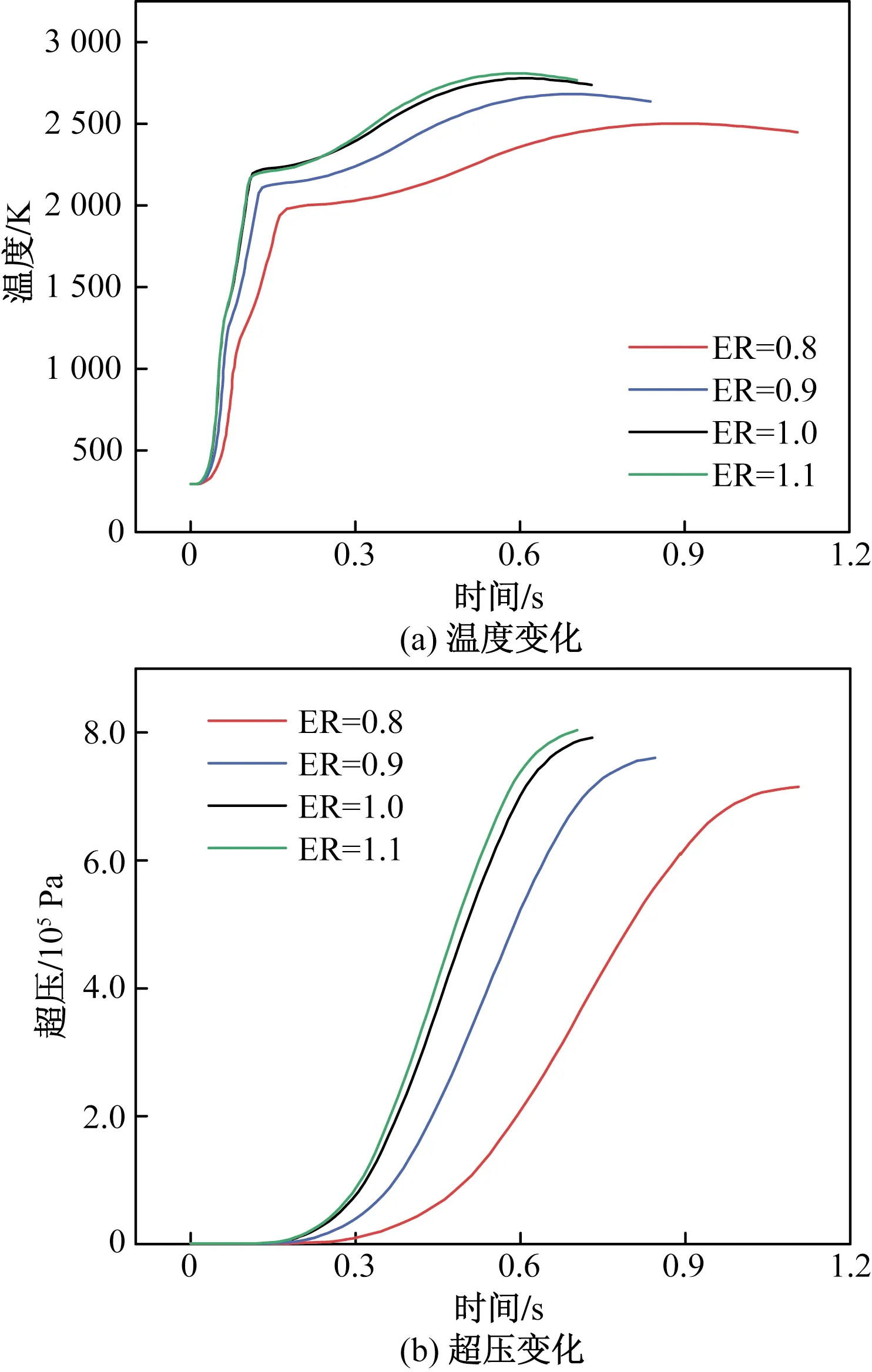
图7 不同燃烧程度情况下监测点1处的温度和超压变化Fig.7 Variations of temperature and overpressure at monitoring point 1 under different combustion degrees

图7(b)给出了算例2、算例8～算例10共4种ER值情况下监测点1处的超压变化。可以看到，不同燃烧程度情况下的超压变化同温度变化趋势基本相同。随着ER值的增大，超压上升时间逐渐提前，并且出现最大超压值的时间也逐渐提前，整个爆炸过程持续的时间缩短。ER=0.8时最大超压为7.16×105Pa，而ER=1.1时最大超压为8.06×105Pa，比前者提高0.89×105Pa。

4 结论

对室内受限空间中掺氢天然气爆炸事故进行了模拟研究，分析了掺氢比、打火点位置、计算区域是否开放和燃烧程度对掺氢天然气爆炸事故特征和演化规律的影响，得出如下结论。

(1)不同掺氢比下掺氢天然气爆炸温度和超压曲线随爆炸时间的变化趋势基本一致；掺氢比越大，爆炸发生时间越早。

(2)距离打火点位置越近的地方爆炸温度和超压越先剧烈上升。算例2和算例5中监测点1处温度开始变化的时间相差0.2 s左右。

(3)开放空间内掺氢天然气爆炸事故的威力远小于受限空间。在同样条件下，门窗开启状态下爆炸所达到的最大温度较门窗关闭状态下降低543.4 K，而此时超压基本无变化。

(4)燃烧程度对掺氢天然气爆炸威力影响较大。本文当量比为0.8时最大爆炸温度为2 501.5 K，最大超压为7.16×105Pa；而当量比为1.1时最大爆炸温度为2 810.2 K，最大超压为8.06×105Pa，分别比前者升高308.7 K和0.89×105Pa。此外，当量比越高，爆炸时间越短。