FRP-ECC加固钢筋混凝土梁受弯性能研究

王勃 ， 张振

（1.吉林建筑大学土木工程学院，长春 130118；2.吉林省结构与抗震科技创新中心，长春 130118）

0 引言

大量桥梁、房屋因服役时间较长，性能逐渐退化，因此急需对桥梁、房屋进行加固处理。传统的加固方式，如增大截面法、外包型钢法等存在湿作业时间过长，易受环境侵蚀等不足［1，2］，因此需要提出一种新型加固方式。而ECC（Engineered Cementitious Composite）材料主要特点是具有超高韧性，加固时可有效抑制开裂［3，4］。FRP材料（Fiber Reinforced Polymer）即纤维增强复合材料，具有轻质高强、耐腐蚀等特点［5，6］。FRP-ECC复合材料对梁进行加固可以有效提高梁的抗弯承载力［7-9］。FRP水泥砂浆加固混凝土板弯曲性能、加固混凝土梁剪切性能试验研究表明，FRP水泥砂浆加固法可以显著提高结构极限承载力和延性性能［10-12］。文中通过对梁底部使用ECC材料为加固层，并将FRP筋嵌入ECC中对结构加固，用模拟与计算的方式验证加固效果。

1 试件设计

对文献［13］中FRP筋-ECC加固梁进行有限元分析。混凝土强度等级为C40，梁长度为1900mm，净跨度1800mm，截面尺寸为200mm×300mm，保护层厚度为25mm，受拉钢筋为HRB400，受压钢筋为HRB500，箍筋采用HRB400。箍筋在跨中部分间距为150mm，其余部分箍筋间距为100mm。加固梁截面尺寸如图1所示。

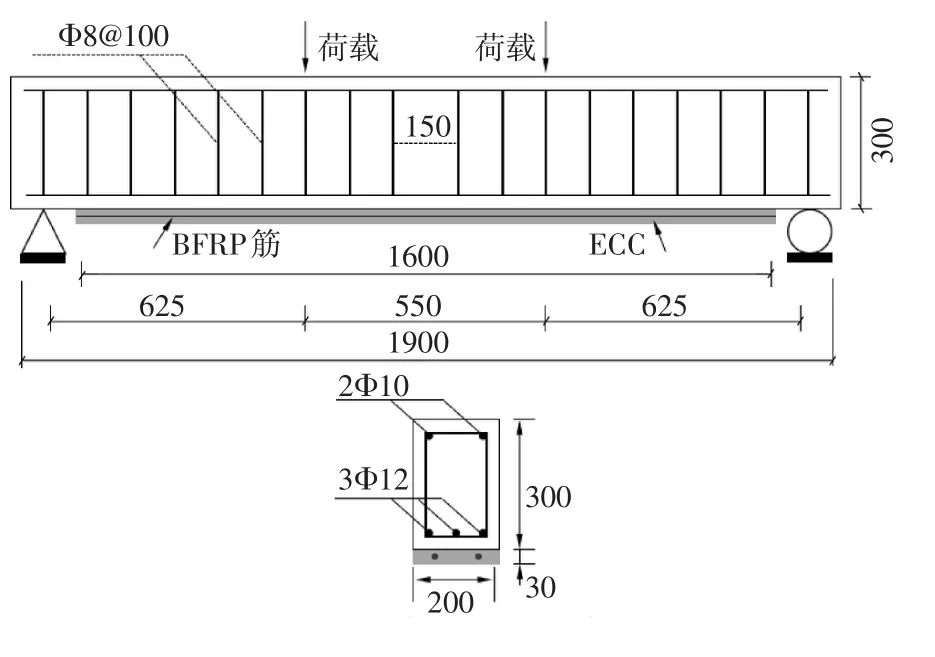
图1 加固梁设计截面尺寸（单位：mm）

ECC材料宽为200mm，厚度为30mm，长度为1600mm，FRP筋位于ECC材料厚度中部，直径为6mm。ECC材料粘贴于梁底部，如图1所示。为增强FRP筋与ECC材料之间的粘结，在FRP筋与ECC之间布置10根直径为6mm的FRP分布筋，如图2所示。

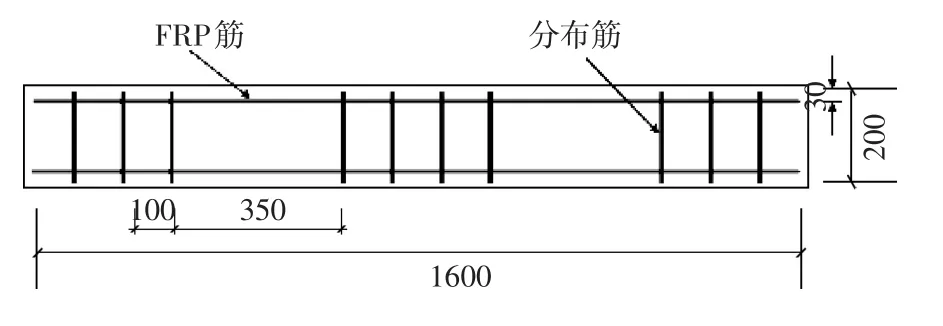
图2 加固层筋材设计尺寸（单位：mm）

2 有限元模型

2.1 材料本构模型

采用ABAQUS三维有限元模型进行分析，混凝土采用8节点线性缩减积分单元，即C3D8R单元，考虑混凝土失效前其塑性变形较为明显，对其进行受力分析时采用塑性损伤模型。ECC材料因为与混凝土同为水泥基复合材料，采用C3D8R单元以及塑性损伤模型对ECC材料进行属性定义。FRP、ECC本构关系如图3所示［13-16］。

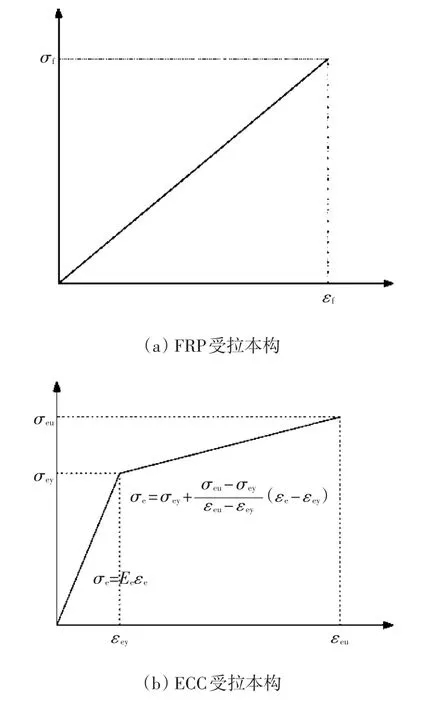
图3 材料本构关系

2.2 边界条件

在梁的上部两处受力点以及底部支座处，均安装宽度10cm的金属垫片，垫片与梁之间的接触设置为绑定，不考虑摩擦力。ECC与梁之间采取绑定的界面粘结方式。钢筋骨架与混凝土之间采用内置区域的约束模式，FRP筋与ECC材料的之间的粘结方式也采用内置区域的界面约束方式。在梁底部支座中线处设置U2=U3=0。加载方式采用位移加载方式。

2.3 有限元模型验证

对钢筋混凝土梁L1及加固层FRP筋配筋率为0.94%和1.41%的FRP-ECC加固梁LEF1、LEF2进行模拟，验证与试验值吻合度。LE、LEF3、LEF4、LEF5为扩展参数试件。LEF1、LEF2、LEF3受拉FRP筋直径为6mm，LEF4、LEF5受拉FRP筋直径为8mm。配筋率为FRP筋截面积之和与ECC截面积之比。将模拟结果与试验结果进行对比，验证模型的科学性。模拟结果如图4～图6所示。

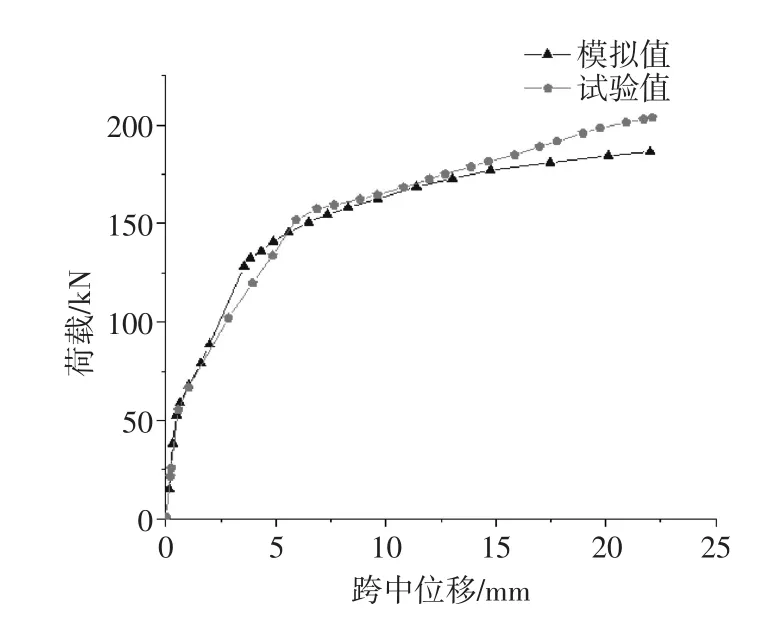
图5 0.91% FRP-ECC加固钢筋混凝土梁LFE1荷载-位移曲线

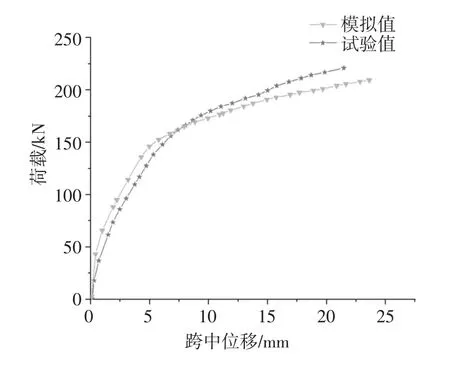
图6 1.41% FRP-ECC加固钢筋混凝土梁LFE2荷载-位移曲线

由图4～图6知，未加固钢筋混凝土梁与加固梁的荷载-位移曲线可分为3个阶段，即混凝土的开裂阶段，混凝土开裂后到钢筋屈服的屈服阶段，以及钢筋屈服后到梁破坏的极限阶段。模拟结果与试验结果吻合较好，验证了有限元模型的准确性。

2.4 有限元结果分析

使用ABAQUS软件进一步探讨不同加固方式对梁的抗弯承载力的影响。LE为使用相同长度与截面尺寸的ECC材料对钢筋混凝土梁进行加固。LFE表示使用FRP-ECC复合材料进行加固，LFE1、LFE2、LFE3、LEF4、LEF5分别表示FRP筋配筋率分别为0.94%、1.41%、1.67%、1.88%和2.51%，有限元建模分析试件如表1所示，荷载-位移曲线如图7所示。

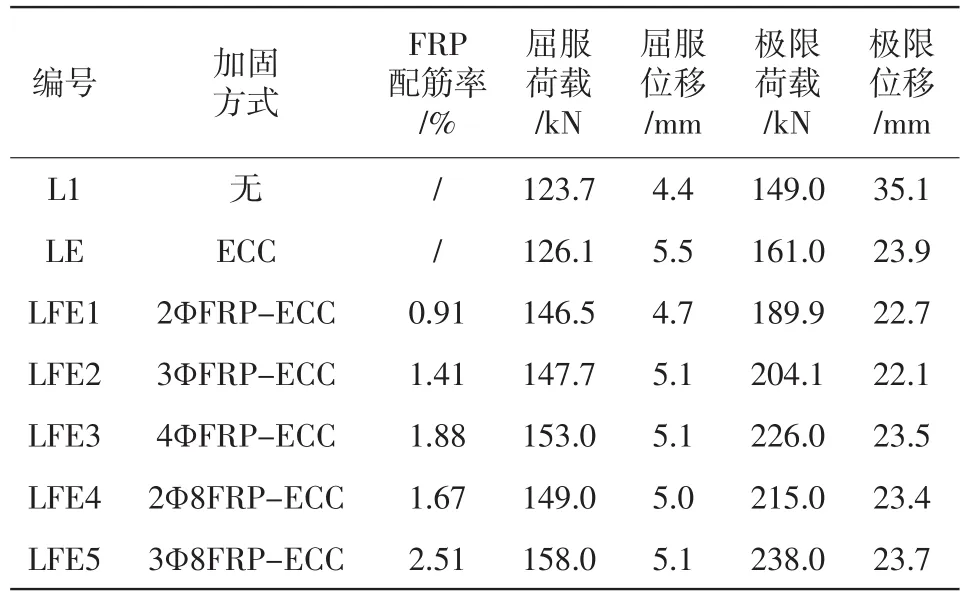
表1 有限元分析结果

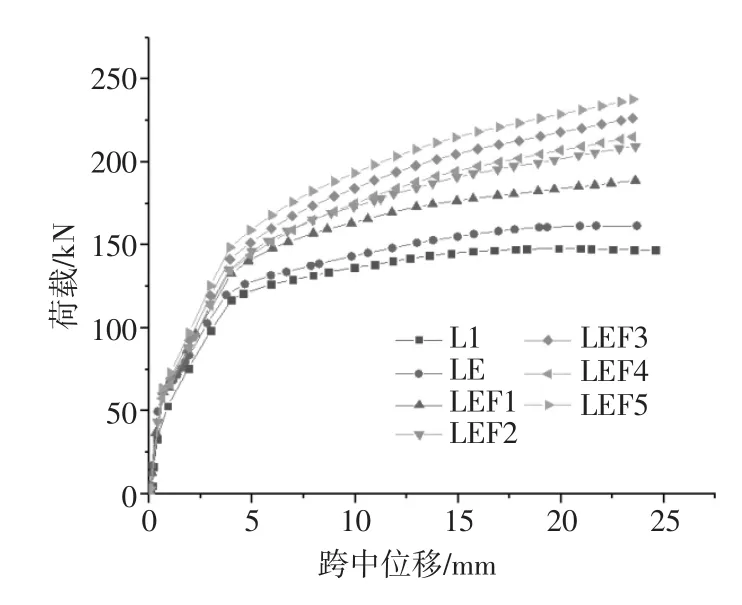
图7 不同加固方式梁荷载-位移曲线

由图7可知，各试件荷载-位移曲线主要分为3个阶段。第一阶段为直线，此时混凝土未开裂，试件斜率与刚度最大；第二阶段曲线斜率减小，此时混凝土出现裂缝，部分受拉混凝土退出工作，导致刚度与曲线斜率减小；第三阶段出现明显的曲线斜率减小，刚度减小，此时混凝土受拉裂缝变宽，钢筋发生屈服。

LE屈服荷载为126.1kN，与控制梁L1屈服荷载123.7kN基本相同。LE极限荷载为161kN，与控制梁L1相比提高8.05%。单纯使用ECC屈服荷载与极限荷载提高不明显。

加固梁LFE1屈服荷载为146.5kN，极限荷载为189.9kN。加固梁LFE2屈服荷载为147.7kN，极限荷载为204.1kN。加固梁LFE3屈服荷载为153.0kN，极限荷载为226.0kN。加固梁LFE4屈服荷载为149.0kN，极限荷载为215.0kN。加固梁LFE5屈服荷载为159.0kN，极限荷载为238.0kN。FRP-ECC加固梁LFE1～LFE5屈服荷载比控制梁L1提高18.4%～27.7%，极限荷载比控制梁L1提高27.4%～59.6%，加固效果明显优于ECC加固梁LE。加固梁LEF1、LEF2、LEF3、LEF4、LEF5屈服荷载差距不大，说明FRP配筋率对屈服荷载影响不明显。加固梁LFE2、LEF3、LFE4、LEF5极限荷载分别比LFE1提高7.5%、13.3%、19.0%、25.2%。

3 抗弯承载力计算方法

3.1 承载力分析

加固梁的极限受弯承载力分析基于以下基本假定［15，16］；1、加固梁的截面符合平截面假定；2、混凝土开裂后，忽略混凝土的抗拉作用；3、加固层计算取ECC中部为计算高度；4、ECC与混凝土之间粘结良好，不发生滑移；5、FRP筋与ECC之间粘结良好，不发生相对滑移。加固梁的截面应变分布如图8所示。

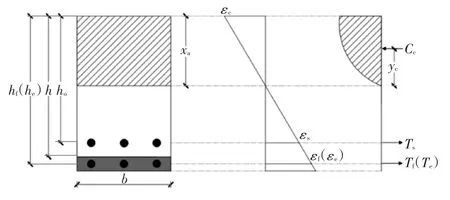
图8 加固梁截面应变分布

加固梁破坏模式主要有两种，混凝土压碎破坏与加固层FRP筋拉断破坏。两种破坏方式之间的界限条件是当FRP筋拉断与混凝土压碎破坏同时发生，与分别为混凝土的极限压应变和FRP筋的极限拉应变。界限破坏时：

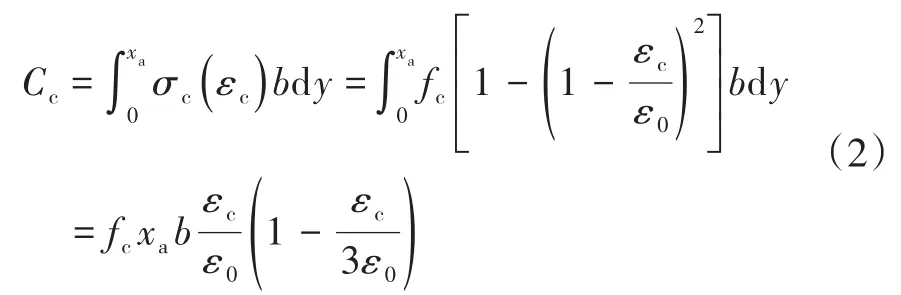
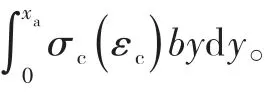
同时，将yc对应的混凝土的应变定义为εcy，则根据的线性关系，可得：

将式（2）式（4）代入式（3）中可得yc

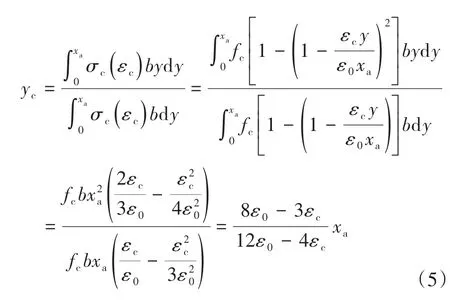
3.2 混凝土压碎抗弯承载力

当混凝土压碎时εc=εcu，发生界限破坏时纵向受拉钢筋发生屈服，加固层中FRP筋未发生断裂，ECC出现裂纹，但ECC可带裂纹工作。εe≤εeu，εc≤εcu和εs≥εsy，εeu为ECC极限拉应变。根据力的平衡得出：

混凝土受压区合力Cc，钢筋提供拉力Ts，FRP筋提供拉力Tf，ECC提供的拉力Te由式（7）表示：

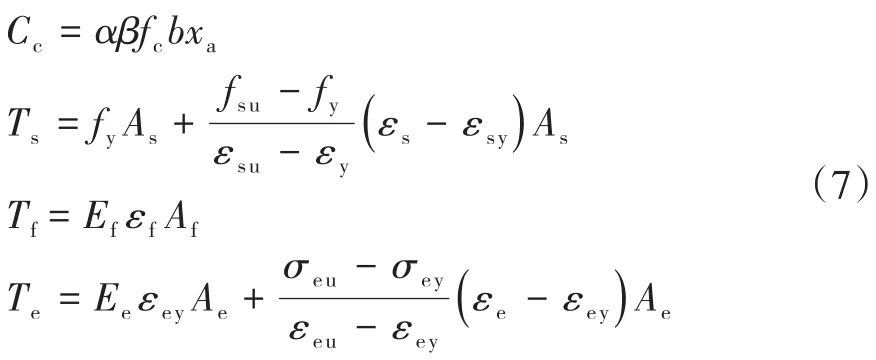
根据平截面假定：

将式（7）、式（8）代入式（6）中，得到关于xa的方程。并根据文献［15］可得α=1，β=0.8，以此求得xa。FRP-ECC加固梁极限抗弯承载力为：

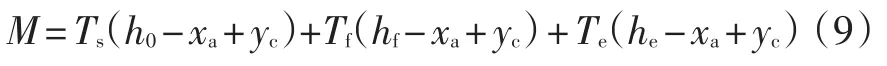
3.3 FRP筋拉断时抗弯承载力

FRP筋拉断破坏，ECC材料达到极限状态，梁受压区混凝土未压碎，钢筋发生屈服，即εc≤εcu，εf≤εfu，此时混凝土压力、钢筋拉力、ECC拉力与FRP筋拉力的计算公式可表示为：

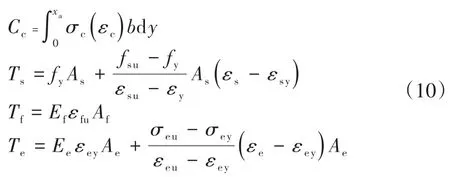
根据平截面假定：

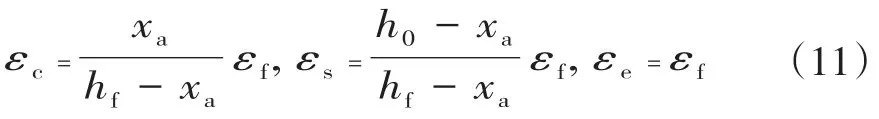
将式（10）与式（11）代入Cc=Ts+Tf+Te中，可以求得混凝土受压区高度xa。则FRP筋断裂时，FRP-ECC加固梁的极限抗弯承载力为：

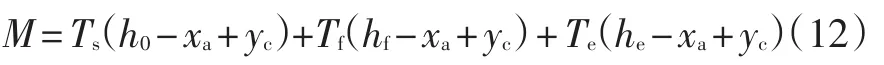
3.4 计算结果分析

根据表2中FRP筋-ECC加固梁极限荷载的计算值与模拟值对比显示，计算值与模拟值的误差在-5.0%～0.2%之间，计算值与模拟值吻合较好，提出的计算方法为FRP-ECC加固工程应用提供参考。

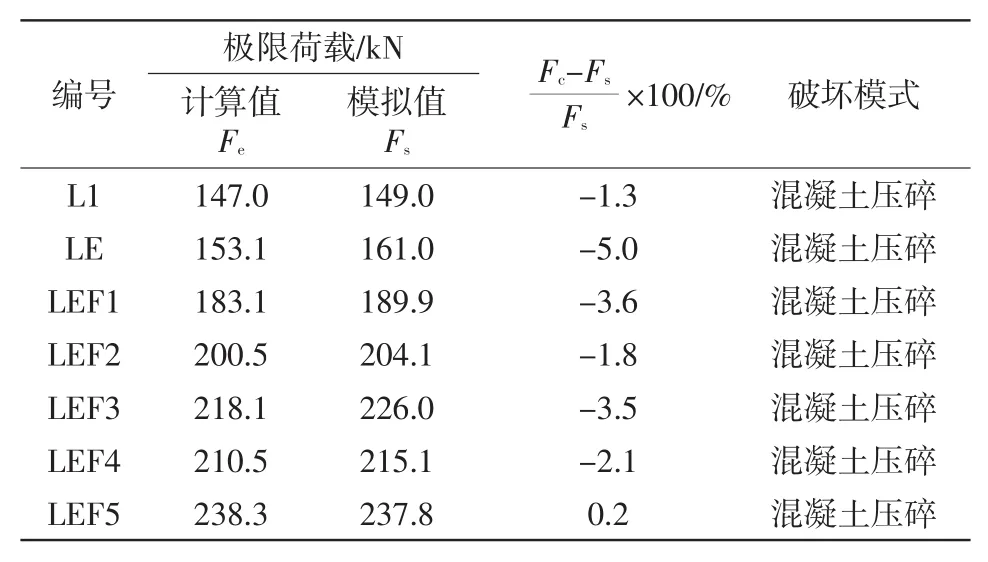
表2 计算值与模拟值对比

4 结语

文中对FRP-ECC加固钢筋混凝土梁力学性能进行研究，研究FRP筋配筋率对抗弯承载力的影响，得到以下结论：

（1）单独使用ECC材料加固，使用FRP-ECC复合材料加固，均可提高梁的屈服和极限抗弯承载力。使用FRP-ECC加固梁的力学性能要明显优于单独使用ECC加固梁；

（2）FRP-ECC加固梁的屈服荷载比控制梁提高18.4%～27.7%。FRP配筋率0.94%、1.41%、1.67%、1.88%、2.51%加固梁屈服荷载差距不大，FRP配筋率对屈服荷载影响不明显。

（3）FRP-ECC加固梁的极限抗弯承载力比控制梁提高27.4%～59.6%，极限抗弯承载力随着FRP筋配筋率的增加而增加。FRP配筋率1.41%、1.67%、1.88%和2.51%加固梁的极限抗弯承载力比0.91%加固梁分别提高7.5%、13.3%、19.0%和25.2%。

（4）提出FRP-ECC加固梁抗弯承载力计算方法，与有限元模拟结果误差在-5.0%～0.2%之间，为FRP-ECC加固结构应用提供参考。