基于风险的油田注水管线的维护决策优化方法
王 强,陈健飞,陈丽娜,刘庆福,仇东泉,赵 杰
(1. 胜利油田技术检测中心,东营 257000; 2. 海上石油工程技术检验有限公司,东营 257000;3. 东营市特种设备检验研究院,东营 257000; 4. 胜利油田检测评价研究有限公司,东营 257000)
目前,针对注水系统的决策优化少有研究,梁永图等[1]以管网运行能耗与注水井注入量偏差损失成本总和最小为目标建立了混合整数非线性规划模型,较大程度上提高了注水系统运行的稳定性与经济性。辛胜超等[2]以管网运行费用最小为目标函数建立模型,确定注水站最佳注水方案及每口注水井的节流压力降,采用分段线性化变为MILP模型简化求解,验证了模型在油田节能降耗应用中的可行性。张昕等[3]针对注水井区域划分及配水间的站址优化问题建立了混合整数非线性规划模型,采用模拟退火遗传算法进行两阶段求解得到最优的配水间位置,并将模型应用于大庆油田某区块进行油田注水管网布局优化。RUAN等[4]通过对大量注水系统数据的计算和评价,确定了注水系统最佳运行方式的选择方法,形成了注水系统最佳运行方式的五条判别规则,给出了确定运行方式的数学模型和运行参数的优化方法。陈利琼等[5]为管线维护决策优化问题提出了两种优化方法,即效用函数法和有限费用优化法[6-7]。效用函数法[8]是在管道风险维护决策问题中,从经济损失、环境损害、人身损失三个方面去考虑,而定义的多准则函数,以效用值最大的方案为最佳决策。尹斌等[9]采用损失函数法对油气集输管线进行维护决策优化,并应用于某原油外输管线,维护效果显著。赵志峰等[10]以管道外腐蚀中的土壤腐蚀数据为基础,建立了管道土壤腐蚀多因素分类决策树。马大中等[11]采用管网的压力、流量等运行数据,提出了一种基于大维数据驱动的管网泄漏监控模糊决策方法。以上有关注水管道决策优化的研究主要集中在运行能耗和管网布局优化,并未涉及维护决策优化;而现有的油气管道决策优化研究均没有把风险与决策有机融合,存在一定的片面性。
本工作以油田注水管道的风险评价结果为基础,建立油田注水管道决策优化数学模型,结合油田注水管道运行方案、措施、设备状况、人员管理等因素,采用期望值和决策树法,将风险控制在可接受范围内,以追求最低的投入成本,并制定相应风险管控优化措施。
1 油田注水管道决策优化数学模型
决策优化系统由注水管道风险评价、决策准则、状态集、决策集、决策费用集、概率分布集、状态损失集、决策树八部分组成。
1.1 注水管道风险评价
将T-S模糊故障树与注水管道危险有害因素及失效特征相结合,根据可获取的油田检测数据,构建注水管道失效模糊子集及T-S故障重要度分析算法,改进建立在油气管道风险评价基础上的评价指标及取值,得到注水管线失效的概率。参考管道公司规定的油气管道沿线地区等级,根据注水管道失效特点及失效后果,从人身伤害、环境污染及停产风险三个角度划分注水管道失效后果级别。将注水管道失效概率及失效后果划分为五个等级,采用对称风险矩阵来表示注水管道的风险等级。
1.2 决策准则
注水系风险管控最理想的状态是:经济损失最小、生命损失最小、环境损失最小。然而,在追求低生命损失和环境损失的同时,必然会引起更高的经济损失。依据管道可接受风险水平的 ALARP原则,在决策过程中,首先把风险控制在可接受的中低风险,再追求最小的经济损失。
1.3 状态集
a为状态变量,指注水管道系统可能处于的不同状况,A为状态集,是全体状态所构成的集合,记为A={a}。注水管道决策优化系统中管道的失效状况包括:断裂(a1)、穿孔(a2)、不失效(a3),则A={a1,a2,a3}。
1.4 决策集
b为决策变量,指为了降低风险而提出的每一个方案,B为决策集,是全体决策所构成的集合,记作B={b}。
注水管道决策集的建立思路如下:结合注水管线风险评价T-S模糊故障树的底事件,从第三方破坏、腐蚀、误操作、设计、自然灾害五方面给出相对应的解决措施。采用穷举法对决策措施进行排列组合,形成多种决策方案,把决策措施间有冲突的方案剔除,剩余I种降低风险的决策方案,建立决策集B={b1,b2,b3,……bj}。
1.5 决策费用集
不同的决策方案,投入的成本不同,为了在符合风险等级的前提下,追求最小的经济投入,需要计算每种决策方案的经济性。c为决策费用变量,是指每种决策所需要投入的成本,其全体集合称为决策费用集C={c}。
考虑实施每个措施所需要耗费的人力物力,以及停产所带来的经济损失,计算每个措施每条管道每年所需要投入的费用。计算决策集中I种决策方案的费用,组成决策费用集C={c1,c2,c3,……cj}。
1.6 概率分布集
在某一决策下,系统所处的状态,称为该决策下系统出现的后果,记为D=(b,a)。后果出现的可能性,称为后果发生概率p,记为p(b,a)。在某一决策b下,所有状态的概率分布称为展望,记作P={p1,D1;p2,D2;……pj,DJ}。
在油田注水管道维护决策优化系统中,状态的发生概率是在不同维护决策bj下,注水管道出现断裂a1、穿孔a2、不失效a3三种状态的可能性,分别表示为:pi1=(bj,a1);pi2=(bj,a2);pi3=(bj,a3),显然最后得到pi1+pi2+pi3=1。
1.7 状态损失集
计算不同管道状态所造成的经济损失,把状态的损失数量化,称为状态损失变量,记为h,其全体集合,称为状态损失集,记作H={h}。
对管道管理公司来说,一般从经济损失、生命损失和环境破坏(损失)三个方面进行考虑管线的失效后果损失[12-17]。由货币量化准则,将注水管道断裂、穿孔、不发生故障,三种事故状态量化,建立状态损失集,记为H={h1,h2,h3}。
1.8 决策树
决策树图是运用图论的方法,来表达决策过程的一种树形图,通常由决策点、方案分枝、状态结点、概率分枝和结果点等几部分组成,见图1。决策分析时,首先,要从左向右按书写的逻辑顺序横向展开,画出决策树图;其次,把各个方案的损益期望值从右向左逐一进行计算;最后,各方案的损失期望值从左到右分级比较,进行方案选优。

图1 决策树结构图Fig. 1 Structure of decision tree
根据注水管道风险评价结果,结合决策组合解决的风险因素,对该决策组合下注水管道的风险等级重新评定,若处于高风险,则代表该决策组合下注水管道存在不可接受的风险,决策组合弃用,若处于中低风险,计算出在该决策组合下注水管道出现三种状态的概率。分别计算处于中低风险各种决策组合下的期望值,期望值最小的决策组合即为最优决策。
2 油田注水管道的决策优化过程
2.1 注水管道风险评价
2.1.1 计算注水管道的失效概率
建立子事故树主要考虑第三方破坏、腐蚀、设计、误操作及自然灾害五个方面,分析引发注水管道失效的关键因素。结合现场调研参数,将注水管道失效子事故树进行剪枝和优化处理,从而建立注水管道T-S模糊故障树,如图2所示。包含32个基本事件(X1~X32),19个中间事件及20个T-S门。

图2 注水管道T-S模糊故障树Fig. 2 T-S fuzzy fault tree for water injection pipeline
基于现场调研参数、管道完整性管理规范QSY.1180.3-2014及肯特法,通过专家调查权重法,采用模糊子集来描述根节点故障概率,将风险发生可能性划分为5个等级,见表1。
2.1.2 注水管道失效后果分析
国内外关于注水管道高后果区识别并没有明确范围,参考管道公司规定的油气管道沿线地区等级,将注水管道两侧各200m、泄漏点上下游管段各100 m区域作为注水管道事故的影响范围。注水管道失效导致的污水泄漏,会引起高压水伤害、大面积污染、生产中断等事故;在自然保护区、水源地等发生泄漏,更会造成严重的环境污染事故;建(构)筑物直接占压及不符合安全距离占压的注水管道泄漏,会对周围居民的财产甚至生命构成威胁。综合以上因素将注水管道失效后果划分为五个等级。
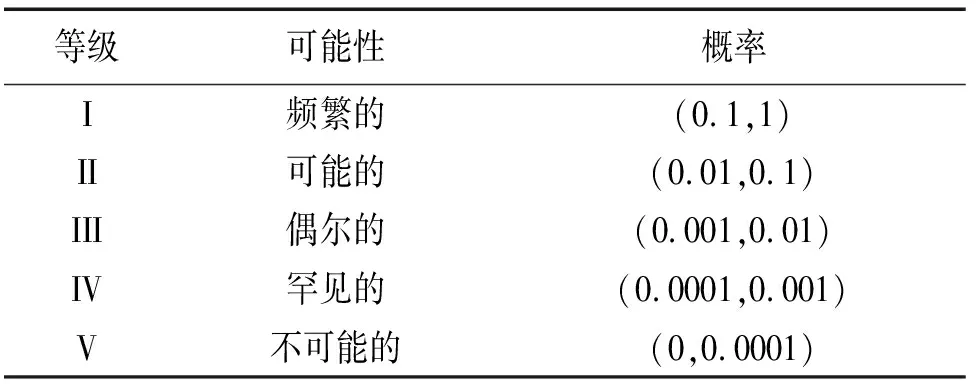
表1 风险发生可能性的等级标准Tab. 1 Level of probability for risk occurrence
2.1.3 建立风险矩阵
基于发生概率和失效后果风险矩阵图可以对风险进行定性评价。它在乘积法的基础上用模糊的概念实现了优化,分别用纵横坐标对发生概率和失效后果进行衡量。本工作将注水管道失效概率及失效后果划分为五个等级,采用对称风险矩阵来表示注水管道风险等级。注水管道失效概率、失效后果及风险等级划分见表2所示。注水管道风险矩阵见图3所示。I~V对应风险等级分别为低、较低、中等、较高和高。

表2 注水管道失效后果、失效概率及风险等级的划分Tab. 2 Classification of water injection pipeline failure consequences, failure probability and risk levels
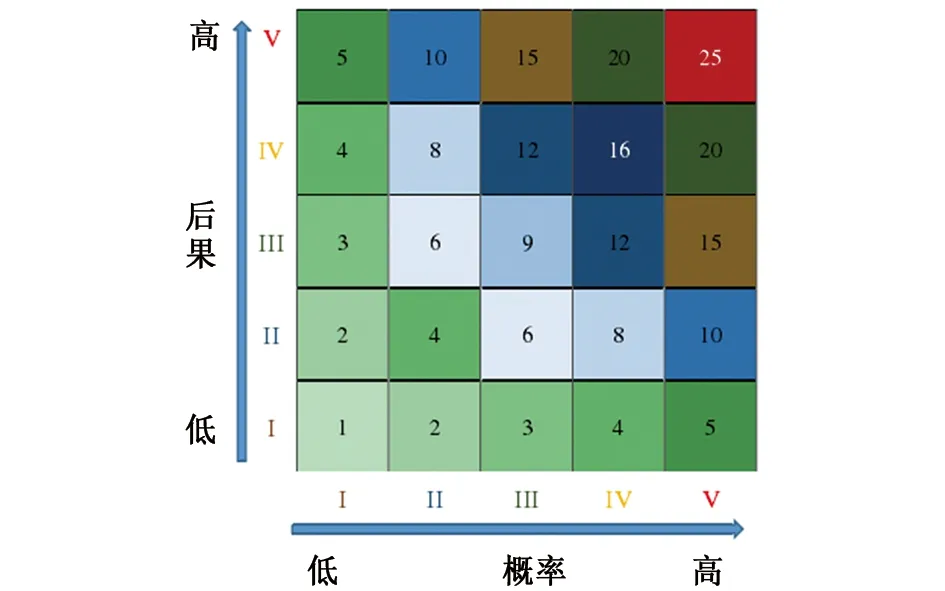
图3 注水管道的风险矩阵图Fig. 3 Risk matrix of water injection pipeline
结合管道风险矩阵图,采用风险分值和风险等级最终展示风险计算结果,以满足投资决策的需求。
2.2 建立注水管道的状态集
注水管道输送介质主要为水,管道状态可分为:断裂、穿孔、正常。建立注水管道状态集A。
A={a1,a2,a3}={断裂,穿孔,正常}
(1)
2.3 建立注水管道决策集
建立决策集的主要思路是结合注水管线风险评价的底事件,从第三方破坏、腐蚀、误操作、设计、自然灾害五方面给出相对应的解决措施,详情见表3。
表3所示腐蚀因素中“特定腐蚀环境”,“特定大气腐蚀环境”属于客观因素,无法通过相应决策改变,同样,开发较早的胜利油田的注水管线管径较小,没有管道内检测的条件,因此“内检测周期长”无法给出相应措施。由表3得到注水管道失效因素风险控制的10条措施,建立注水管道决策集B。第六条措施"更换管材"可有效解决管材内腐蚀中管材耐腐蚀性差、内防腐失效的问题,第五条措施“添加缓蚀剂”可有效解决管材内腐蚀中内防腐失效的问题。“更换管材”包含“添加缓蚀剂”,因此实施“更换管材”,即不需要实施“添加缓蚀剂”。依此建立注水管道决策集B。
B={b1,b2,b3,……,b766,b767,b768}
(2)
2.4 建立决策费用集
计算实施每条措施需要耗费的人力物力,以及停产带来的经济损失,核算每条管道每年需要投入的费用,见表4。
每种决策包含1~9个决策措施,每个决策措施的费用明细见表4,通过计算每种决策的费用,建立决策费用集。
C={c1,c2,c3,……c766,c767,c768}
(3)
2.5 建立概率分布集
采取不同的决策解决相对应的失效因素,因此每一种决策组合下都对应有发生管道断裂、穿孔、正常对应的概率。建立注水管道不同决策下的概率分布集pij,其中i={1,2,3,……766,767,768},j={1,2,3}。
P={pi1,pi2,pi3}
(4)
2.6 建立状态损失集
由货币量化准则,将管道断裂、穿孔,两种事故状态量化,建立状态损失集。
E={e1,e2,e3}={管道断裂200万元,管道穿孔50万元,管道正常0元}
(5)
2.7 决策树的建立
由于决策组合共有768种,种类过多,在这里只给出决策树的示意图,说明思想方法。
如图4所示,方框代表决策结点,圆圈代表机会结点,三角形代表终止。由注水管道风险评价的结果,结合决策组合解决的风险因素,对该决策组合下注水管道的风险等级重新评定,若处于高风险,则代表该决策组合下管道存在不可接受的风险,决策组合弃用,若处于中低风险,计算出在该决策组合下注水管道三种状态的概率。分别计算处于中低风险各种决策组合下的期望值,期望值最小的决策组合即为最优决策。

表3 注水管道失效因素的风险控制措施Tab. 3 Risk control measures for failure factors of water injection pipeline

表4 决策费用明细表Tab. 4 Decision cost schedule

图4 决策树示意图Fig. 4 Schematic diagram of decision tree
2.8 比选最优决策
决策的费用期望值包括实施决策的成本以及在该决策下的状态损失,把每种决策的期望值数量化,记为e,其全体集合记作E={e}。

(6)
式中:Ei为第i种决策下的损失函数。Ci为第i种决策下的决策费用。Hj为第j种管道状态损失。Pij为第i种决策下,第j种管道状态下的概率。
风险处于中低风险的决策中,MinEi对应的决策组合即为最优决策。
3 决策优化实例
实地对某油田某段注水管道进行数据采集,该注水管道沿线人口密度较大,管道上方人口活动较为频繁,容易给管道施加外应力,缩短管道寿命;管道用地标志情况较清晰地标明管道路由走向及管道与公路、铁路、沟渠及江河的所有穿越处,但存在标志物缺失问题;由于注水管道输送介质为含有腐蚀性介质的水,管道运行温度大于40 ℃且运行压力高于10 MPa,满足管道发生腐蚀的内部环境;管材选用20号钢,耐蚀性较差,无法有效抵御内腐蚀风险;管道沿线土壤电阻率小于10 Ω·m,表明土壤含水率及含盐量较高,管道外防腐层一旦破损,管道的外腐蚀问题尤为突出;另外,管道外防腐措施采用单一的防腐层,并没有对管道施加阴极保护,外防腐措施单一。
采用Python编程实现风险识别与决策优化的过程,对某油田某段注水管道进行数据采集并录入软件,计算得到导致该注水管道风险增加的主要因素有:地面活动频繁、管材耐腐蚀性差、无阴极保护。表5为针对每个因素采取的对应措施。

表5 针对每个因素采取的对应措施Tab. 5 Corresponding measures for each factor
将4组措施进行排列组合得到15种决策方案:(1) 加装管道套管;(2) 加装管道标记;(3) 更换管材;(4) 加装管道阴极保护;(5) 加装管道套管、加装管道标记;(6) 加装管道套管、更换管材;(7) 加装管道套管、加装管道阴极保护;(8) 加装管道标记、更换管材;(9) 加装管道标记、加装管道阴极保护;(10) 更换管材、加装管道阴极保护;(11) 加装管道套管、加装管道标记、更换管材;(12) 加装管道套管、加装管道标记、加装管道阴极保护;(13) 加装管道标记、更换管材、加装管道阴极保护;(14) 加装管道套管、更换管材、加装管道阴极保护;(15) 加装管道套管、加装管道标记、更换管材、加装管道阴极保护。
程序计算每种决策下的风险等级、失效概率及经济损失,见表6。
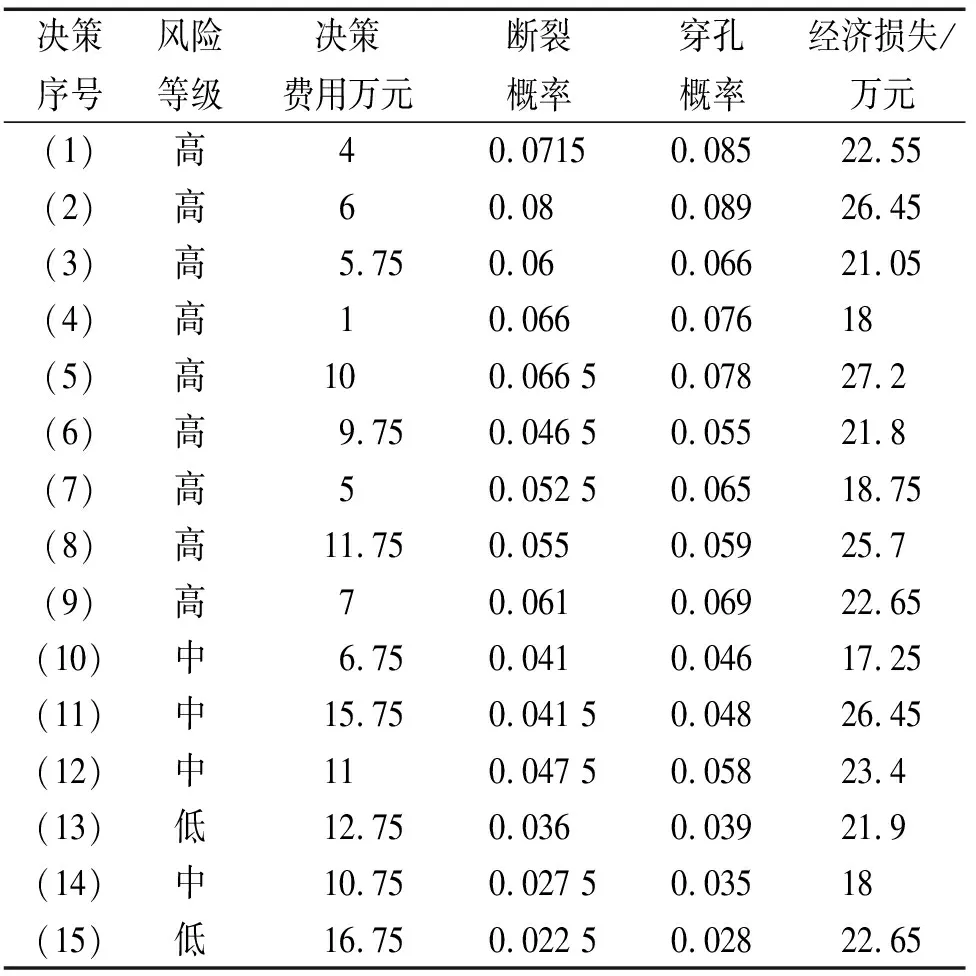
表6 各个决策条件下的预算及损失计算结果Tab. 6 Budget and loss calculation results for each decision condition
由表6得:执行决策(1)、(2)、(3)、(4)、(5)、(6)、(7)、(8)、(9)时,管道仍处于高风险,故决策(1)~(9)作废,对比管道处于中、低风险时的经济损失,决策(10)的经济损失最低,则决策(10)为最优决策,即:更换管材、加装管道阴极保护。
4 结论
(1) 基于T-S模糊故障树的注水管道风险评价结果,引入决策准则、状态集、决策集、决策费用集、概率分布集、状态损失集、决策树建立了注水管线的决策优化数学模型。
(2) 结合注水管线风险评价的底事件,从第三方破坏、腐蚀、误操作、设计、自然灾害五方面给出相对应的解决措施,计算实施每条措施所需要的人力物力,以及停产所带来的经济损失,核算每条措施每条管道每年所需要投入的费用,由货币量化准则,将管道事故状态量化。最终通过决策树,将风险控制在中低风险以下,计算期望值,选出最优决策,提出了优先控制风险,再比较经济性的决策优化新方法。

