城市生活垃圾收运系统仿真与优化研究
张矢宇,李发亮,辜子瑱,陈梓禾,庄涵飞,田志武
(1.武汉理工大学 交通与物流工程学院,湖北 武汉 430070;2.武汉环境投资开发集团有限公司,湖北 武汉 430013)
基于可持续发展的战略要求,节能减排与绿色环保的生产生活方式及发展理念,绿色化、低成本与高效率的生活垃圾收运系统成为了新的发展目标。垃圾收运设施的扩展、系统低碳化[1]、垃圾转运站选址[2]及垃圾运输线路优化等研究[3-4]是垃圾运输领域的研究重点。此外,以减少系统对环境影响程度为目标的研究[5-6]也层出不穷。但目前这些研究较少涉及垃圾收运系统整体运行效率上存在的问题。随着物流仿真技术和软件的出现,利用Witness、Flexsim、Arena等软件对相关物流系统进行仿真,能够使得问题分析更加明显直观,且方案仿真效果良好。但相关研究主要集中在物流配送中心选址、码头作业、仓库管理模式[7]、企业生产物流作业模式等建模仿真[8],鲜见对城市生活垃圾收运系统的仿真研究,对城市生活收运系统优化方案的仿真研究更为稀少。
基于AnyLogic软件,构建城市生活垃圾收运系统仿真模型,以及带时间窗的VRP优化模型。以武汉市杨园街道生活垃圾收运系统为例进行实证研究,通过仿真模型的现状仿真,发现其存在的问题,根据优化模型,求解出最佳优化方案,利用已建模完成的仿真模型,对优化后的新系统进行仿真,验证其可行性和有效性。从而提升城市生活垃圾收运系统效率、降低成本,并促进城市的可持续发展。
1 仿真模型构建
AnyLogic是一款基于智能体,以复杂系统设计方法论为基础的仿真软件,广泛应用于生产制造业、物流供应链、行人疏散、以及城市规划设计的建模与仿真中,对相关行业的运作优化起到了关键作用。同时,它也具备系统动力学建模、离散事件分析的能力,在有复数智能体存在的复杂系统的建模仿真上,更是优秀的辅助与应用工具[9-10]。就其功能及应用范围而言,在对城市生活垃圾收运系统的建模仿真中,AnyLogic是一个强有力的分析工具,其具备的功能可以使各垃圾投放点、转运站、车辆等要素尽可能的接近实际并映射于系统中,输出要素可自行选择对象及表现形式,能够更加直观地反映系统真实的运作情况。
1.1 仿真流程分析
城市生活垃圾收运系统仿真流程如图1所示。当仿真开始时,系统各节点按照既定参数运转,首先垃圾收集车辆从垃圾转运站出发,按照确定线路在各垃圾投放点进行垃圾收集作业,在收集作业完成后将垃圾运往转运站,清洗消毒后进行第二次运输,直至所有垃圾投放点垃圾均收集完成;待垃圾转运站暂存垃圾超过转运车辆载重吨时,转运车辆开始运转,将转运站的垃圾运往垃圾处理中心,直至将转运站的所有垃圾转运完成。
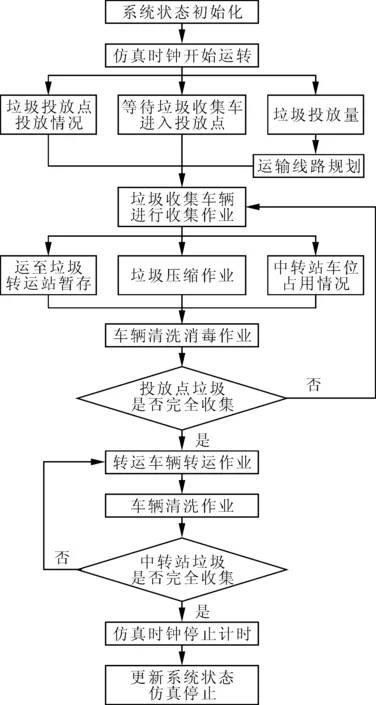
图1 城市生活垃圾收运系统仿真流程
1.2 智能体类别的确定
为了满足系统仿真的各项需求,对城市生活垃圾收运系统的作业内容进行分析,同时把作业内容作为仿真系统运转更新的必要桥梁。因此,根据系统的运作流程及仿真流程,总结出城市生活垃圾收运系统仿真事件列表,如表1所示。

表1 仿真事件列表
由表1中所述的9个仿真事件,可在此仿真系统中共创立7个智能体类,包括垃圾投放点Agent、垃圾收集车辆Agent、转运站Agent、压缩机Agent、转运站工作人员Agent、垃圾转运车辆Agent、垃圾处理中心Agent,它们之间的关系与状态变化过程如图2所示。
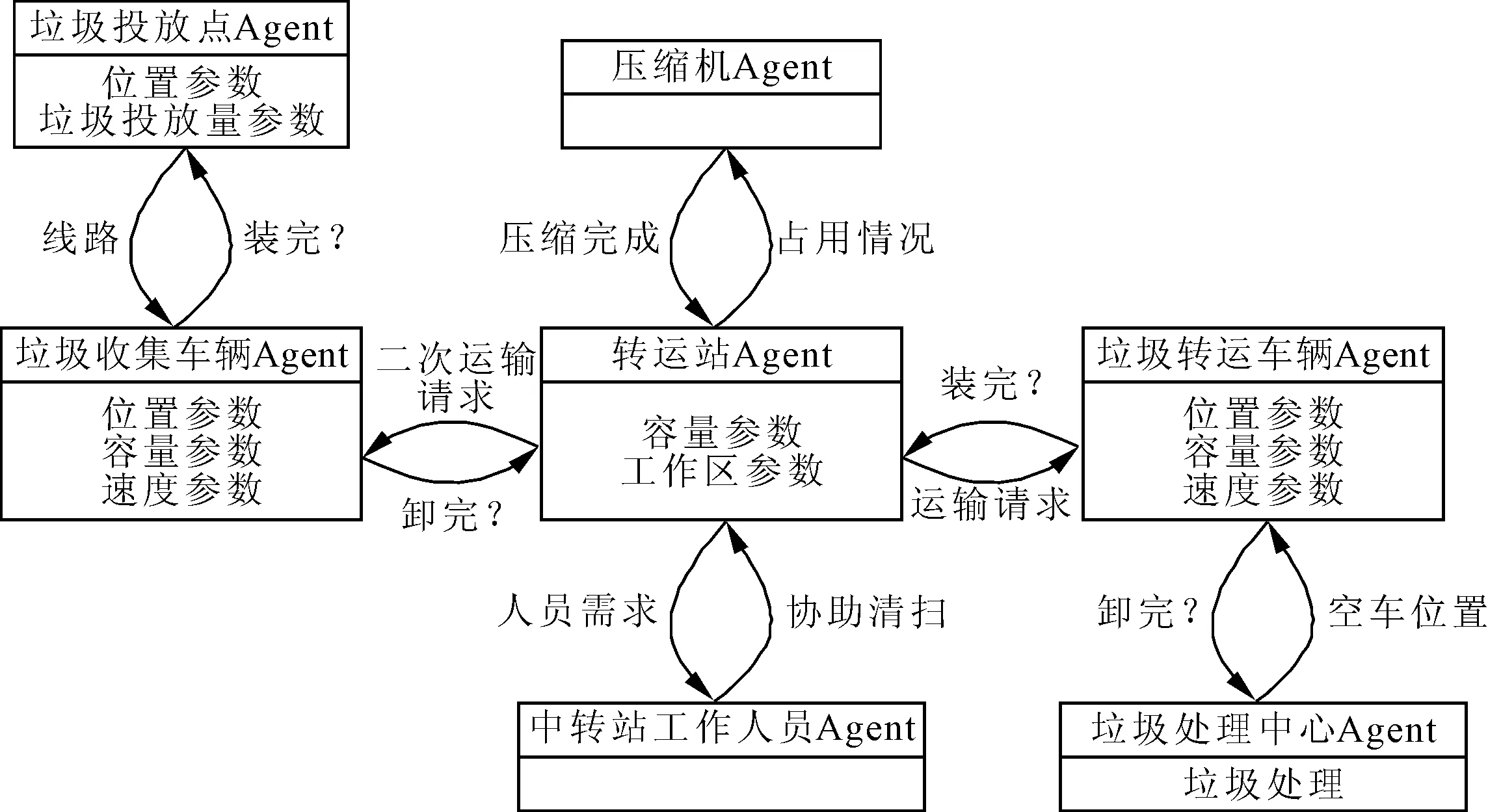
图2 仿真智能体设置
1.3 仿真参数设置
根据上述仿真事件及智能体的设置,可得到垃圾收集车辆、垃圾转运车辆、转运站工作人员、垃圾转运站、垃圾处理中心共5个实体元素。为了能更真实准确地反映系统运作情况,对其进行运行参数设置,包括数量、速度、排队规则等,具体如表2所示。

表2 仿真参数设置
2 优化模型构建
优化模型的构建在于解决系统存在的问题,目前针对我国城市生活垃圾收运系统优化的研究主要集中在布局节点优化、收集线路优化与收运计划优化,旨在提高系统运行效率、降低系统运作成本。而对于节点布局,由于转运站、处理中心需要收集并处理许多不同地区的生活垃圾,且选址必须远离城市中心,其占地面积大、建设成本高、环境污染大,在能够满足当前需求的基础上,一般不考虑对其进行变更。鉴于此,笔者聚焦于垃圾收集线路以及垃圾收运计划的优化,以解决系统效率低、成本高的问题。其中,不同地区垃圾收运系统上下班时间不同、收运车辆车型不同、数量不同、收集模式也有较大差别,因此对收运计划的优化更适合根据实际案例进行分析后做出细微调整。
2.1 基于时间窗的VRP模型
在垃圾收集线路优化上,生活垃圾收运具有及时性、快捷性的特点,可以将其看作带软时间窗的VRP问题。模型可描述为垃圾收集车辆从转运站出发,前往收集点进行垃圾收集工作,已知每辆车的载重量及垃圾收集点的垃圾投放量;每条运输路线经过的垃圾收集车辆数不超过2,完成收集工作后,垃圾收集车辆必须返回垃圾中转站,所有收集车辆均停放在中转站。每辆运输车单次运输会产生相应的固定费用,且运输费用与运输距离成正比。由于时间窗的限制还存在惩罚成本,收集车辆提前或延迟完成均会受到惩罚。此外,由于收集车辆的载重限制,一旦收集到的垃圾重量之和超过收集车辆的最大载重量,便要受到相应惩罚。故在考虑车辆启动成本、超重成本及时间窗约束的总成本最小化模型可以描述为:
(1)
式中:i,j为垃圾收运系统节点;k为垃圾收运车辆;M为垃圾收集车辆总数;qi为第i辆垃圾收集车辆的最大载重吨;N为垃圾收集点总数量;gi为第i个垃圾收集点的垃圾投放量;c1为每辆垃圾收集车辆投入工作的固定费用;dij为节点i至节点j的距离;c2为车辆单位距离运输成本;Sk0为第k辆车开始前往垃圾收集点的时刻;Ski为第k辆车达到垃圾收集点i的时刻;ti为车辆在垃圾收集点i处的服务时间;tij为车辆由收集点i行驶到收集点j所经过的时间;v为垃圾收运车辆行驶速度;ej为垃圾收集点在时间窗内的最早时间;lj为垃圾收集点在时间窗内的最晚时间;pe为车辆早到的等待成本;pl为车辆迟到的惩罚成本;ω为车辆超载的惩罚系数;xijk表示车辆k是否从收集点i行驶至j;yik表示垃圾收集点i的收集工作是否由车辆k完成。
约束条件:

(2)
(3)
(4)
xijk∈{0,1},i=0,1,…,N,
j=1,2,…,N,k=1,2,…,M
(5)
yik∈{0,1},i=0,1,…,N,k=1,2,…,M
(6)
(7)
式(1)共包含了5个部分,分别为垃圾收集车辆投入工作的固定成本、运输里程成本、超重惩罚成本、车辆提前到达的等待成本和迟到带来的惩罚成本;式(2)表示垃圾收集点i的收集工作由车辆k承担,对于垃圾投放量较大的点最多可由两辆车辆运输;式(3)表示对垃圾收集点进行收集作业的车辆k是从垃圾收集点i行驶来的,保证了前置节点的统一性;式(4)表示从收集点到达收集点处的车辆为车辆k;式(5)表示车辆k是否从收集点i行驶至收集点j,若过程发生,那么xijk=1,否则为0;式(6)表示若垃圾收集点i的垃圾由车辆k完成,那么yik=1,否则为0;式(7)表示车辆k达到垃圾收集点j处的时间Skj与到达上一收集点i处的时间Ski的数量关系,且仅当车辆经过两处收集点i与j时才有上述关系。
由于垃圾收运系统的复杂性以及约束条件的特殊性,使得垃圾收集车辆路径问题为NP-hard问题,故在选择求解算法时,应选择高效率、寻优能力强的算法。在诸多算法中,遗传算法作为大规模问题的现代启发算法,非常契合垃圾投放点数量较多的垃圾收运系统,且就性能而言,遗传算法具有计算效率高,搜索能力强的特点,故采用遗传算法对上述模型进行求解。而传统遗传算法在交叉、变异概率不能发生变化的基础上,容易出现过早收敛或局部最优的现象。因此,选择自适应遗传算法作为此模型的求解算法,通过动态调整交叉与变异的概率,达到克服早熟与随机漫游问题的目的[11]。
2.2 优化评价指标选取
为了对优化方案的成效进行评价和分析,需要设立优化评价指标。由于优化的目的在于降低系统运行成本、提高系统运行效率,归纳整理现有研究成果,主要可从经济投入、运行状况两方面进行评价[12-14],在经济投入的评价上,可分为投资费用与运作费用两部分[15],由于优化未涉及硬件设施的更改,故选取系统运作成本作为优化方案经济评价的具体指标,其大小由车辆运输成本、人工成本,垃圾处理成本、管理维护成本等共同决定。在运行状况评价上,结合仿真流程与优化模型考虑的范围,在收运系统覆盖率、垃圾车利用率、收集点满溢率等14个三级指标中[16],从中选择车辆作业时间以及车辆利用率作为优化方案运行评价的具体指标。其中车辆作业时间包括垃圾收集车辆作业时间与垃圾转运车辆作业时间,两者作业时间共同决定了系统的总运行时间。车辆利用率为车辆作业时间与车辆总运行时间的比值。
3 武汉市杨园街道实证分析
3.1 杨园街道生活垃圾收运系统现状
杨园街道总面积为5.24 km2,可大致划分为4个区域共78个生活垃圾投放点,各垃圾投放点垃圾分区收集,收集频率为1日两次,全地区日垃圾收运总量为80 t。街道仅有一个垃圾转运站,共有垃圾收集车辆16辆,每辆收集车辆根据吨位的不同按照既定收集线路行驶,从转运站出发最终回到转运站位置,运行速度为15 km/h,直至每个投放点收集两次后停止工作。杨园街道生活垃圾均运往长山口垃圾处理中心。负责垃圾转运的车辆共3辆,运行速度为40 km/h,直至将转运站的所有暂存垃圾全部运往处理中心后结束工作。经过实地调研发现,杨园街道垃圾收集车辆的运输线路主要根据收集人员经验进行设计,未进行合理的规划,在垃圾收集线路的设计上有待改进。此外,还存在转运车辆排队等待时间较长的问题,使得系统运作效率下降。杨园街道生活垃圾收运系统布局如图3所示。根据垃圾收集线路,系统平均每天垃圾收集线路总距离约为167.59 km。
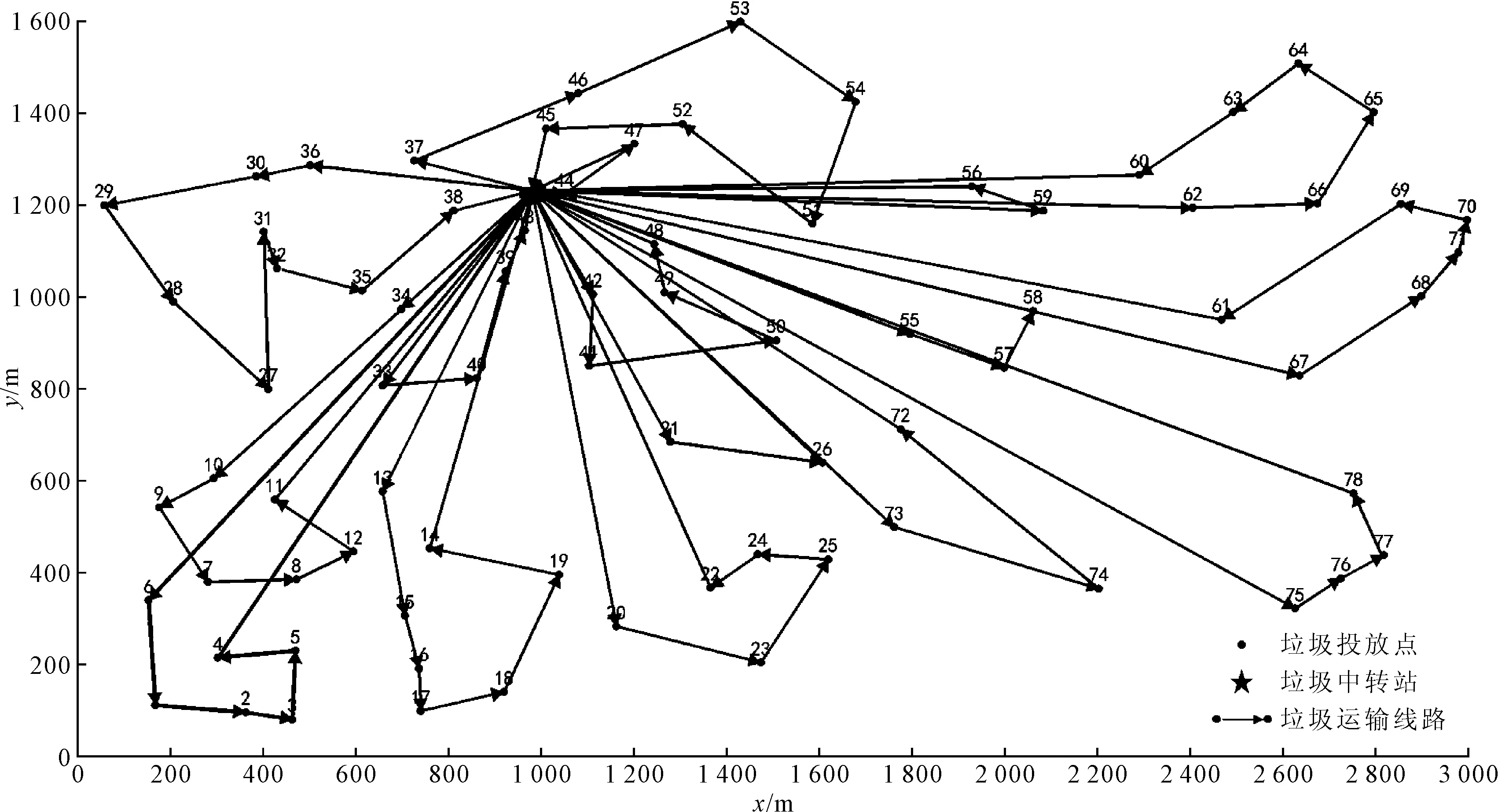
图3 杨园街道生活垃圾收运系统布局
3.2 现状仿真结果
将实地调查所得相关数据及参数输入仿真模型中,得到车辆作业时间、车辆利用率、系统运作成本的仿真结果,分别如图4~图6所示。
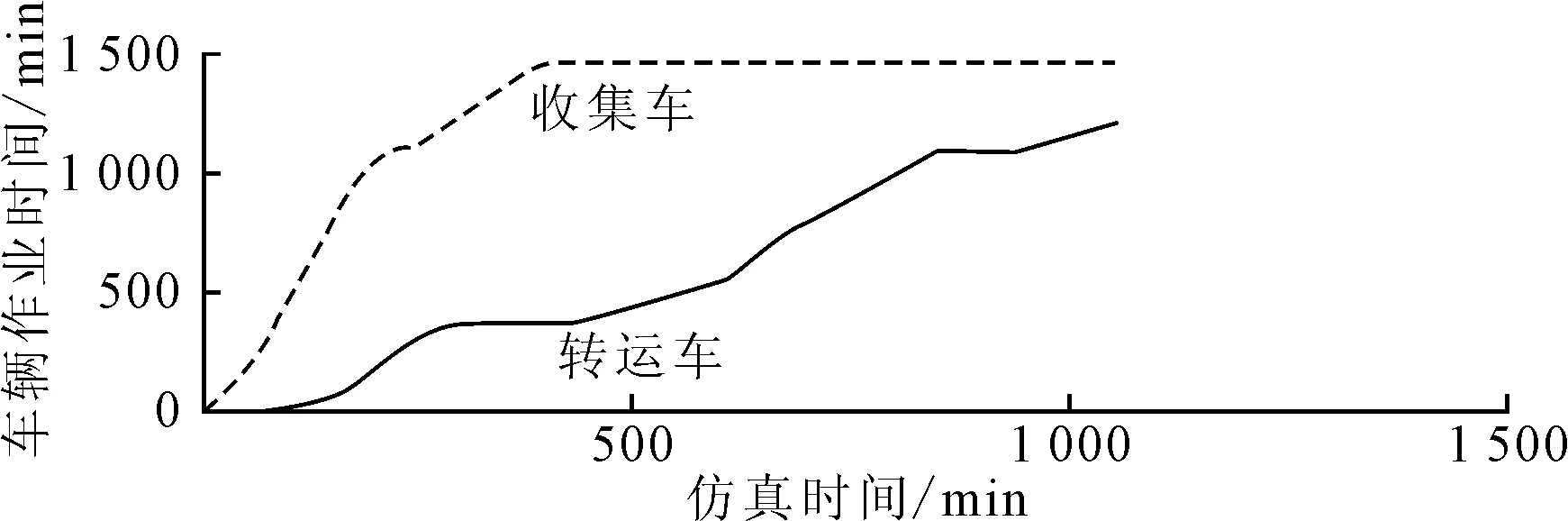
图4 车辆作业时间仿真结果
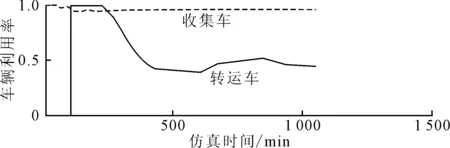
图5 车辆利用率仿真结果
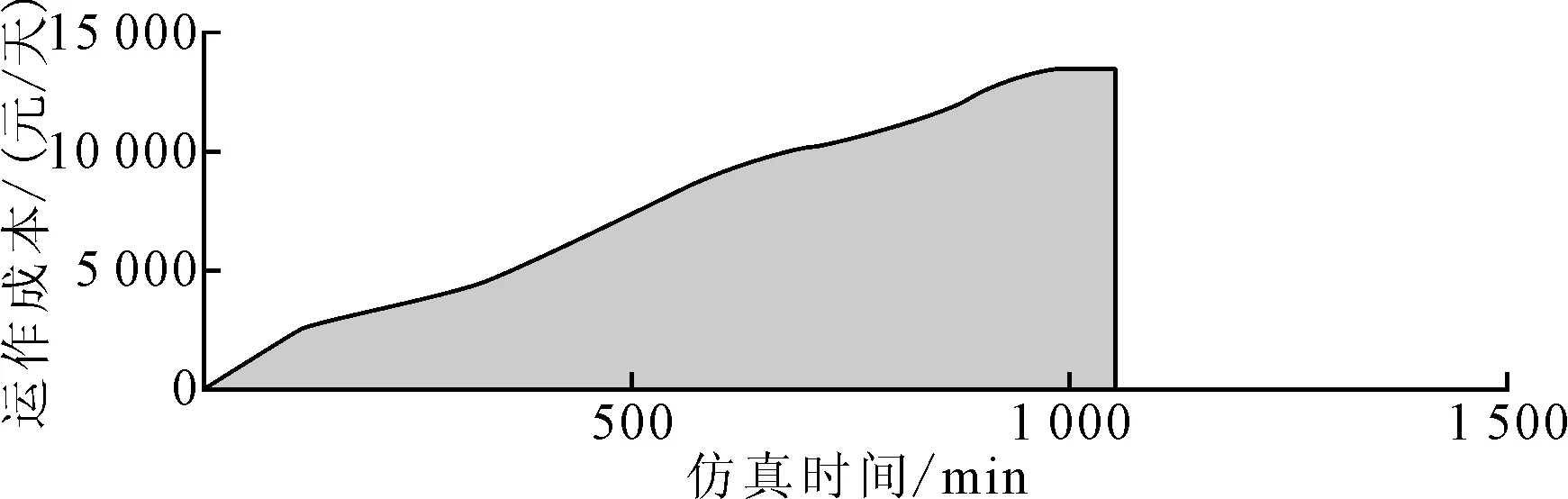
图6 系统运作成本仿真结果
3.2.1 车辆作业时间
车辆作业时间为所有收集车辆作业时间的总和,处于先快速增长后慢速增长最后趋于稳定状态的趋势,说明在系统运转过程中,部分垃圾收集车辆提前完成了所有的作业任务,使得增长趋势变缓。而垃圾转运车辆在系统开始运转一段时间后才开始运行,其作业时间总体上呈缓慢增长的趋势,其中部分时段处于一个稳定值,说明垃圾转运车辆必须等待收集车辆收集一定量的垃圾后才能开始运作,但是由于排队等待原因,导致作业时间停滞不增,直至最后一辆转运车辆返回垃圾转运站,整个系统才停止运转。仿真结束时间为1 059 min,共17.65 h(实际工作时间为凌晨2点至晚上7点)。尤其是垃圾转运车辆,工作时间跨度太大,时间太长,导致垃圾转运车辆负荷过大,垃圾转运车辆司机压力过大。
3.2.2 车辆利用率
从图5可以看出,垃圾收集车辆利用率在系统开始运转时为100%,随后有所下降最后维持在一个较为稳定的状态,在97%上下小幅度波动,说明垃圾收集车辆一直处于忙碌状态,等待时间较少。而垃圾转运车辆在系统开始运转一段时间后从100%不断下降,最后在50%上下范围波动,垃圾转运车辆较垃圾收集车辆相比利用率不高,大部分时间处于与等待空闲状态,说明垃圾转运车辆在整个工作时段中等待时间过长,占整个工作时间的一半,极大的降低了转运车辆的利用率。
3.2.3 系统运作成本
由于系统运作成本由车辆运输成本、人工成本,垃圾处理成本、管理维护成本等共同决定,在仿真模型中,除车辆运输成本与车辆运输里程成正比外,其他各项均与时间成正比。从图6可以看出,系统运作成本的增长速率一直在发生变化,呈现先快后慢、再快再慢的循环变化趋势。说明系统开始运转时,所有车辆、设备均处于工作忙碌状态,成本上升较快;之后部分车辆进入排队等待阶段,由于处于空闲状态,导致成本上升较慢;在垃圾收集车已停止工作后,成本依然上升较快,说明垃圾转运车辆的单位成本较垃圾收集车辆单位成本更高,对系统运作成本的影响更大。仿真结束时,系统运作成本为13 452.53元/天,全年总成本约为491万元。
3.3 优化方案
针对上述系统中存在的问题,考虑到实际可行情况,对杨园街道现有垃圾收运系统做出以下调整,以达到优化效果。
(1)垃圾收集车辆收集线路优化。按照优化模型式(1)~式(7),构建杨园街道生活垃圾收运系统优化模型。根据上文自适应遗传算法,在MATLAB软件上编写算法程序,结合实际情况反复试验后,最终确定自适应遗传算法的参数为:种群规模S=100,最大进化代数X=300,收集车辆的固定启动费用c1=300元/辆,超载惩罚系数ω=10 000,时间窗惩罚系数pe=400,pl=400。经过数次运行,进化在第87代得到最优解,遗传算法种群进化过程如图7所示,优化后的收集线路方案如图8所示。结果显示,运算过程在开始时搜索最优解速度较快,最优值下降较快;随着进化代数的增加,曲线趋于平缓状态,最优值下降变慢,最终逐渐趋于收敛,并在87代开始进化到此问题的最优解,未出现早熟现象。杨园街道垃圾收集最优成本为4 708.72元,由于初始种群为现行垃圾收集线路,故较优化前相比,成本共减少了559.15元。根据优化结果,系统平均每天垃圾收集线路总距离约为151.95 km,与优化前相比缩短了15.64 km。
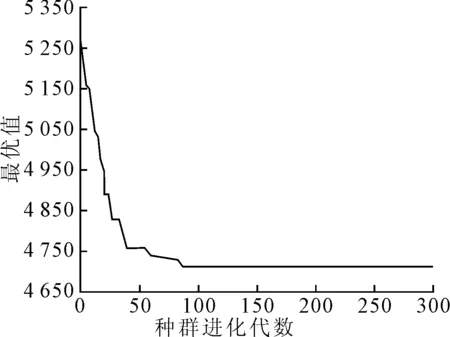
图7 遗传算法种群进化过程
(2)生活垃圾转运车辆运行时间优化。在车辆作业时间仿真结果中,生活垃圾转运车辆是在生活垃圾收集车辆开始工作一段时间后才开始工作,导致系统总运作时间延后。若垃圾转运车辆能与垃圾收集车辆同时开始工作,垃圾转运车辆运行时间将会向前平移,则可减少系统总运行时间。为达到此目的,每日开始工作时垃圾转运站内必须要存有一定数量的垃圾,而暂存一整晚垃圾对转运站附近环境有一定影响。在进行充分消毒与气味处理后,每晚可暂存3整车的垃圾,以确保第二天系统开始运作时转运车辆能与收集车辆同时运行,可减少系统每天总运作时间。
(3)生活垃圾转运车辆发车间隔优化。由于案例中长山口生活垃圾处理中心服务于多个街道,每个街道有着相应的转运车辆发车时刻表对发车时间进行控制,发车间隔统一为10 min。总体而言,转运车辆在垃圾处理中心的到达间隔也为10 min,近似来看垃圾转运车辆的到达符合指数分布。而每辆转运车辆在垃圾处理中心停留作业时间约为20 min,根据统计学与概率学原理,在保证系统总作业时间不延长的情况下适当增加发车间隔,可有效降低转运车辆的排队时长,提高转运车辆利用率并减少系统运作总时间。结合杨园街道实际情况,最终将发车间隔调整至15 min。
3.4 优化后仿真结果
优化后车辆作业时间、车辆利用率和系统运作成本3个指标的仿真结果如图9~图11所示。
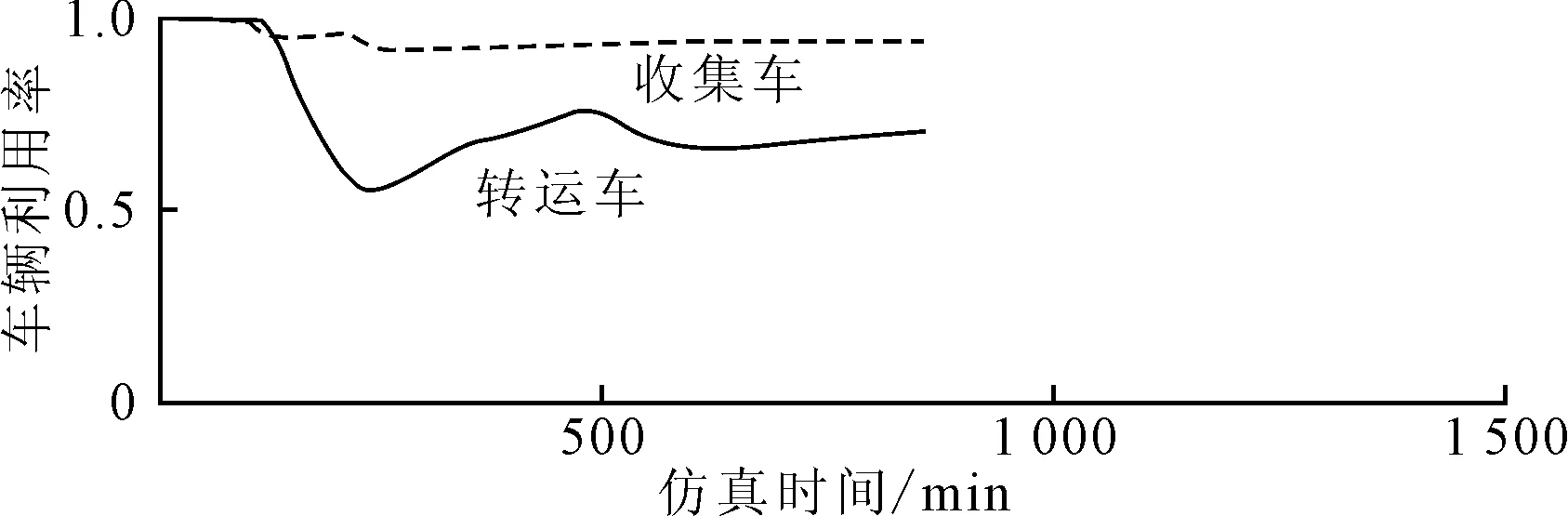
图10 优化后车辆利用率仿真结果
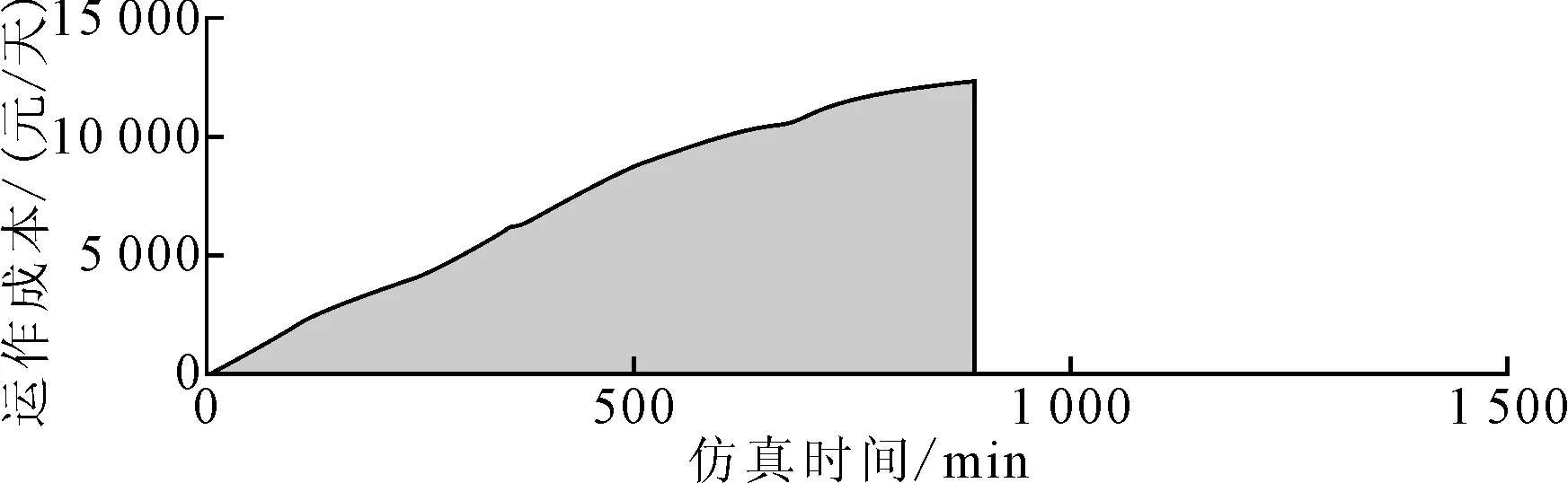
图11 优化后系统运作成本仿真结果
①从车辆作业时间来看,优化后垃圾转运车辆从0时刻开始运行,系统每天运行总时间减少到了883 min,与优化前相比减少了176 min,从而可以缩短转运站、处理中心的工作人员、卡车司机等的工作时间,以便能够充分休息,更好地进行垃圾收运和处理工作。②从车辆利用率来看,收集车利用率较原来相比没有太大变化,依然保持接近97%的态势。而垃圾转运车辆利用率虽然开始时下降较快,但之后有所上升,最后在70%上下波动,与优化前相比,垃圾转运车辆最终利用率提高了近20%,且在系统运转时间段内没有任何时刻低于50%。③从系统运作总成本来分析,成本曲线与优化前相比斜率有所上升,曲线波动幅度变小,这是由于车辆等待时间减少,行驶距离增速增大造成的,且最终成本由13 452.53元/天减少到了12 461.80元/天,每年共可节省36.1万元。
4 结论
(1)构建基于Anylogic的城市生活垃圾收运系统仿真模型并进行系统仿真,可以发现城市生活垃圾收运系统存在的问题并验证优化方案的可行性和有效性。
(2)构建基于时间窗的VPR模型并求解,以此提出的优化方案,在垃圾收集线路缩短,系统总运行时间缩短、车辆利用率提高等方面有显著效果。
(3)城市生活垃圾收运系统中收集线路的规划、车辆运行时间安排和发车间隔等对系统运作效率和成本有着重大的影响。建议在城市生活垃圾收运系统建设与发展中,科学规划垃圾收集线路和车辆运行时间,并制定合理的发车时刻表从而提升系统运作效率、降低成本。
——以信阳市平桥区为例

