韧性视域下北极航行风险级联效应分析
马晓雪 何佩龙 乔卫亮 刘阳
(1 大连海事大学,公共管理与人文艺术学院,辽宁 大连 116026;2 大连海事大学,航运经济与管理学院,辽宁 大连 116026;3 大连海事大学,轮机工程学院,辽宁 大连 116026)
0 引言
北极航线航行环境正酝酿重大变化并有望在夏季实现全线通航[1],国际社会对北极的关注度也因此变得越来越高。针对北极通航安全风险,目前已经形成了较为完整的研究体系。对于北极航线安全风险模糊性特征造成的认知障碍,李振福等[2]利用盲数理论提出了处理盲信息灰信息等不确定信息的方法;与之类似,后悔理论也被应用于北极航线安全风险分析中[3];另外,王锐等[4]借助灰色系统理论在处理不确定信息方面的优势对北极环境数据中的确定性信息进行了分析。为更好地解决由北极安全风险动态性造成的认知困境,马晓雪等[5]依托动态贝叶斯理论实现了对北极航线安全风险的动态把握。目前应用韧性理论来研究北极安全风险的成果并不多见,付姗姗等[6]依托韧性工程构建了涉及四因素五方面的极地船舶航行框架,为后续研究提供了参考。以上研究多从“人-机-环-管”的框架下认识船舶航行风险,将研究重点聚焦在风险及其后果上,未重点考虑应对风险的能力建设,且缺少对风险间耦合级联效应的探讨;鉴于此,引入韧性理论重新认识北极航行风险,并依托模糊认知图模型深度分析安全风险的级联效应。
1 韧性及韧性视域下北极航行风险认知
1.1 韧性理论及其释义
正如“韧性”释义为跳回的动作,韧性最早被认知是在工程领域并用来解释木材受骤然压力不会断裂的现象。Holling[7]将韧性理论引入生态学并对“生态韧性”的概念做了反复修正,认为韧性属于系统自身特性并决定着系统内部关联的持续性,系统韧性测度以其维持稳态所吸收的扰动量级来计算;随后在 Holling 的研究基础上,Berkes 和Folke[8]Gunderson[9]拓展了生态韧性概念,致力于探索“社会-生态系统”中的韧性思维,重点关注了系统稳态变化;Carpenter 等[10]在此基础上细化了扰动量的具体内涵,将其归结于吸收的扰动量自组织与学习适应程度。随着对系统结构机制运行认识的深入,一种源于适应循环理论的演进韧性概念被提出,Folke 等[11]重点强调了持续韧性适应性转变性,可见演进韧性更关注持续适应并在优化中实现状态恢复的能力。概而言之,作为研究和分析负面事件的新视域,韧性摒弃了传统风险管理规避风险或“亡羊补牢”的消极姿态,从系统自身角度出发,将负面事件内化为稳定状态下的一部分,即为一种“共存”思维。借助“共存”思维所构建的安全逻辑,承认容许并主动应对负面事件。这种安全逻辑普遍被认为应包含吸收适应及变革三个维度[12-15],见表1。因此,总体来看,韧性是系统维持或恢复动态稳定状态的内在能力,保证系统在面对扰动后能够继续运行,以“吸收能力”“适应能力”和“变革能力”为具体表现形式。

表1 韧性能力的内涵要义Table 1.The connotation of resilience
1.2 韧性视域下的风险及北极航行风险的韧性认知
韧性理论继承了传统风险管理与脆弱性研究的优势,从系统角度出发探讨“安全”与“风险”的内在逻辑。Crichton[16]认为风险作为发生损失的概率,应从三方面界定,即危险源脆弱性和暴露度,其中“危险源”指环境中本当存在的风险,“脆弱性”与“暴露度”则决定了系统会不会受到干扰。与其类似,作为韧性理论研究的集大成者,Hollnagel[17]强调了外力在系统韧性建构中引发的负面作用,而这种外力通常源于环境,Hollnagel 的“外力”与Crichton 的“危险源”不谋而合,共同探讨了环境中本当存在的风险造成系统能力变化的关键作用。但不同的是,Hollnagel 等[18]认为“系统面临的风险并不是失效概率造成的,而是系统自身功能变化引发扰动的后果”。这一观点突破了传统脆弱性视角下的风险定义,将风险发生的原因归结于系统自身的功能可变性,从系统能力角度出发探寻“韧性能力”与“安全风险”的内在逻辑。“在扰动前后有效调整系统功能可以维护系统韧性”[19],在Hollnagel 等看来,扰动是造成系统韧性发生变化的关键因素,控制扰动应以调整系统功能为前提。根据前文可知,扰动来源于系统自身的功能变化,因此,若要达到韧性永续,需要从系统功能可变性角度出发反观“风险”,即若要维持系统韧性,需要控制哪些扰动,那么“韧性视域下的风险”便应运而生。然而,扰动并不会“凭空出现”,根据前文可知,外力是系统韧性变化的源头,因此,将“本质性风险”纳入“韧性视域下的风险”范畴。同时,将以本质性风险作用于系统自身引发系统功能变化所形成的扰动视作“诱致性风险”。“本质性风险”与“诱致性风险”共同构成“韧性视域下的风险”内涵,见图1。根据上节对韧性能力的分析,将“诱致性风险”具体分为常规性风险变例性风险与宏观性风险,以此构建新的研究范式,来认识北极航行安全风险,见表2。
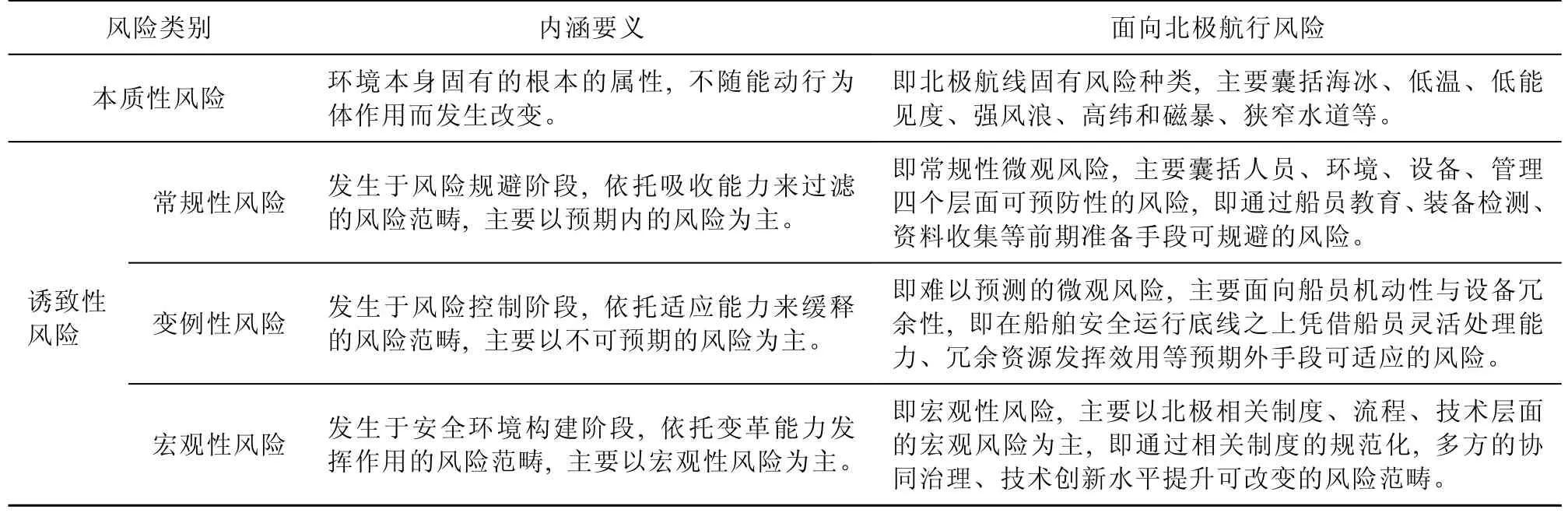
表2 韧性视域下的风险及北极航行风险的韧性认知Table 2.Risks under the resilience perspective and the resilience perception of Arctic navigation risks
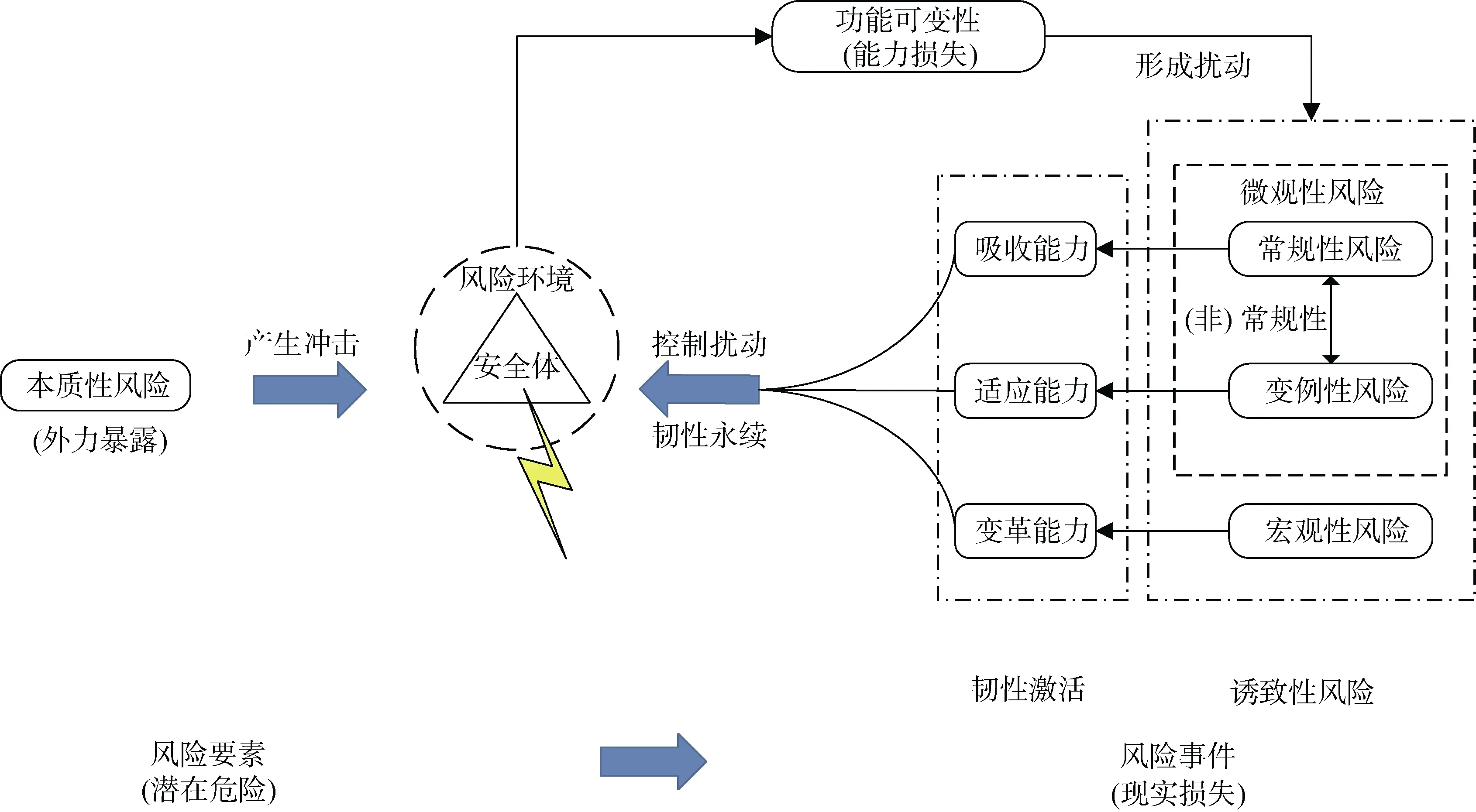
图1 韧性视域下的风险分析逻辑Fig.1.Risk analysis logic from the perspective of resilience
一般情况下,风险通常被认为是一种潜在的危险,而风险事件的发生使潜在的危险转化成为现实的损失[20]。从这个意义上来说,当风险尚未对系统安全产生冲击效果,即风险处于暴露状态时,风险表现为潜在“风险要素”;当风险对系统产生冲击效果,即风险处于冲击状态时,风险表现为“风险事件”(或称“风险事故”)。以潜在危险与现实损失划分“风险要素”与“风险事件”不仅有助于从可变及动态角度掌握风险内涵,更适应了“韧性视域下风险”以及“风险级联效应”的分析要求。
根据表2,确定韧性视域下北极航行风险的典型风险要素(见表3)。

表3 韧性视域下北极航行安全风险要素Table 3.Arctic navigation safety risk indicators under the resilience perspective
长期以来,针对风险管控问题,研究思路基本是基于“人-机-环-管”四个维度,依托“风险识别-风险评价-风险控制”三个环节构建分析模型,以实现风险规避或控制为最终目标[36-37]。与其不同,韧性理论以肯定并接受环境的非安全性和持续变化为前提,将风险管控视角从外部转向对研究对象本身功能可变性的剖析。作为一种新探索,“韧性视域下的风险”正是建立在对功能可变性剖析的基础之上。将“韧性视域下的风险”引入北极航行风险研究,其创新与优势主要体现为以下几点。
(1)传统风险管理研究视角是“由外而内”的,“韧性视域下的风险”是“由内而外”的。这种思维摒弃以外部风险的不确定性为起点对风险问题进行剖析的方式,将研究对象转向北极安全主体自身,实现从“不可控”到“可控”。
(2)传统风险管理研究的最终目标是“风险控制”,“韧性视域下的风险”是“风险适应”。“防不胜防”反映了复杂社会环境下应对风险威胁的被动困境,尤其是在北极这个具有高度不确定性与未知性的研究领域下,传统风险管理模式更是“捉襟见肘”。与传统风险管理模式不同,“韧性视域下的风险”淡化了“风险防御”概念,承认并主张与未知性共存,以追求安全永续,更适用于探讨复杂模糊的北极风险问题。
(3)传统风险管理研究应对风险威胁是“消极被动”的,“韧性视域下的风险”是“积极主动”的。“识别-评价-控制”从侧面反映出风险管理过程的滞后性。类似于病毒变异,北极风险也是持续动态变化的,当我们在识别风险时,风险或早已产生威胁。与其不同,“韧性视域下的风险”从系统自身出发,将风险视为内生产物和功能的逻辑体现了风险管理的态度转向,更利于我们直面北极风险问题。
2 风险级联效应及北极航行风险级联效应的认识
2.1 风险因果关系:风险级联效应的逻辑起点
逆境下的风险并不固定,而是动态变化的,如果忽视风险间的关联性往往会导致风险认知偏差[38]。正如前文所述,韧性理论强调对持续稳定状态的追求,而风险又如此复杂,因此对风险的分析,仅做到认识风险远远不够,有必要准确把握风险间的关系,以保证系统能够实现韧性的永续。
风险级联效应常被简单认为是多米诺骨牌效应,但这显然是不准确也不严谨的。作为理解风险社会的重要视角,“级联”及“级联效应”受到供应链风险管理灾难管理运营风险管理等多个研究领域的关注,但“级联效应”在不同的应用场景中,其概念并不固定。在供应链风险管理中,更倾向于以“风险传播”来定义风险级联效应,将其界定为供应链网络中某个节点发生故障,进而产生连锁反应,放大风险破坏效果的过程[39-40]。在灾难管理领域,Caroleo 等[41]将级联效应定义为特定隐患发生所可能导致的事件链。虽然学界目前对“级联效应”的描述并不一致,但是通过文献梳理发现,目前有关风险级联效应的研究多从风险要素间的因果关系出发来讨论级联过程,Feng 等[42]则借助贝叶斯网络分析定义风险要素及其因果关系,以此为基础探讨风险级联过程的复杂性和不确定性。与之类似,Fang 和Marle[43]开发了决策支持系统框架,构建的网络结构将“节点”视作风险,“边”视作因果关系,以此展开模拟,阐释了忽略项目风险的级联效应会导致决策过程失误的观点。
综合来看,风险间存在着普遍的因果关系,它既是引发风险级联效应的源头[44],也是主要驱动因素。作为“导火索”,风险“因果关系”与“级联”“级联效应”存在着复杂的联系。具体来看,当多个风险要素均未产生扰动效果时,它们之间普遍存在潜在的因果关系,这种关系是静态的,不会对系统安全产生影响。所谓“级联”是指当某个风险要素产生冲击效果后,该要素与其他风险要素间的因果关系便活跃起来,进而激活其他风险要素,形成“风险事件”的过程。所谓风险“级联效应”是指在风险“级联”的基础之上,多个风险要素共同产生冲击效果,驱动因果关系,促成二次甚至更多次级联,形成复杂风险事件链的动态过程。可以说风险“因果关系”是“级联效应”的本质和内生动力,“级联效应”是“因果关系”的外在表现形式,而风险由潜在“风险要素”激活为“风险事件”的过程便是促成“因果关系”转变为“级联效应”的催化剂。
2.2 北极航行风险因果关系
根据级联效应理论分析可知,探讨风险要素之间的因果关系是展开级联效应分析的第一步。因此,依据相关文献资料事故报告及专家意见收集来确定二级指标间的因果关系,见表4。在获取风险要素因果关系后,以此为基础展开北极航行风险级联效应分析。
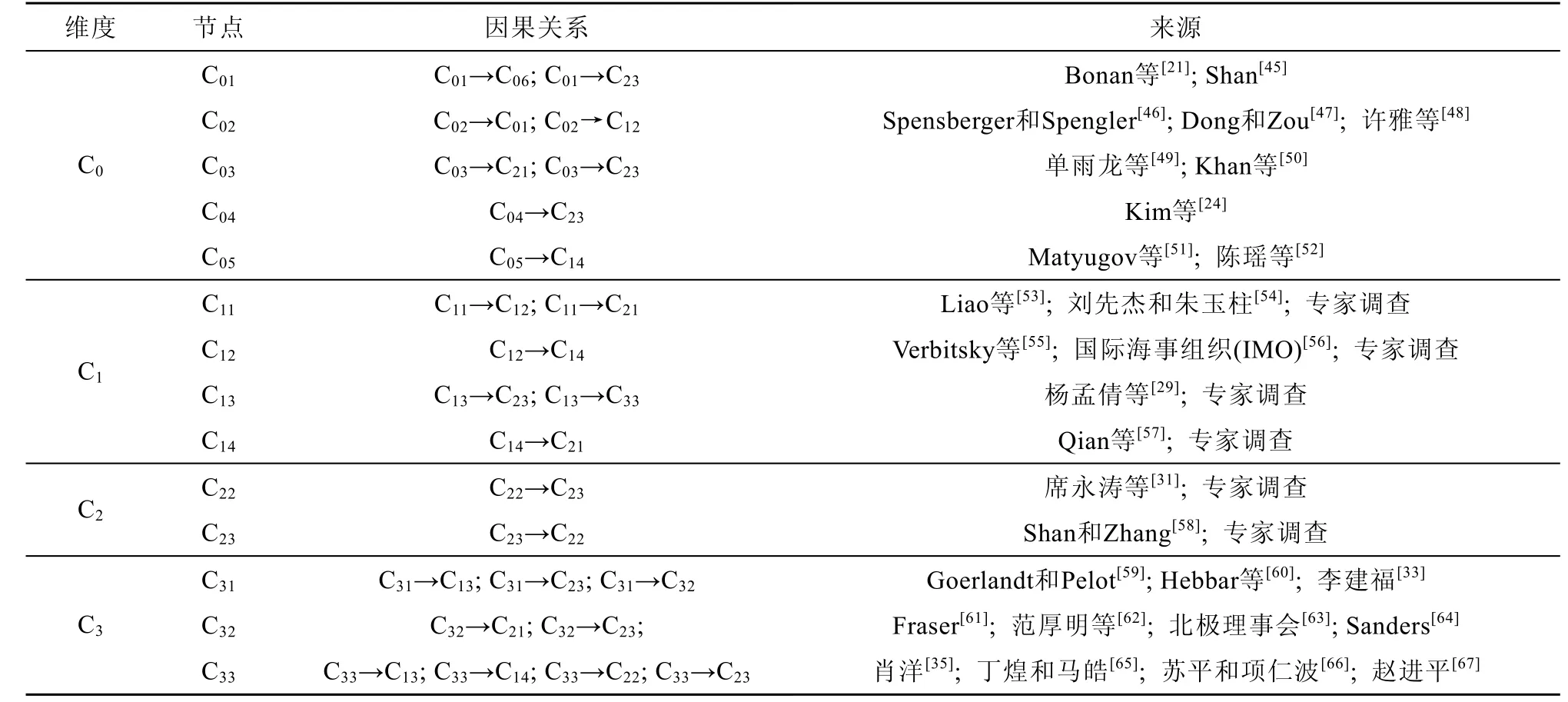
表4 北极航行风险要素因果关系说明及来源Table 4.The causal relationship between the secondary indicators and the references
3 因果知识表示的FCM 分析法
3.1 模糊认知图分析法:表示与推理
Aexlord 首次提出了一种由概念节点有向弧及关联权重三元素所构成的认知图模型并将其应用于商业或制度决策的过程。其中,概念节点代表事件,有向弧表示两者间的因果关系,权重则代表两者间的关联效果。而后Kosko[68]在Aexlord的基础上改进了离散的关联效果并确定了[-1,1]的关联强度区间以适应于模糊推理,模糊认知图(Fuzzy Cognitive Map,FCM)模型应运而生。
(1)FCM 的结构表示
FCM 将模糊理论与网络结构结合。基本图解结构由概念节点和有向弧组成,所有概念节点间的联系及相互作用组成了一个动态系统。图2 即为一个简单的FCM 模型,具有5 个概念节点(C1C2C3C4C5),其中C1对C2存在有向弧,含义为概念节点C1状态值的改变会导致概念节点C2状态值的改变,其关联程度为有向弧权值w12,其余5 条有向弧也具备相似的含义。由图解结构模型可得FCM 邻接矩阵。
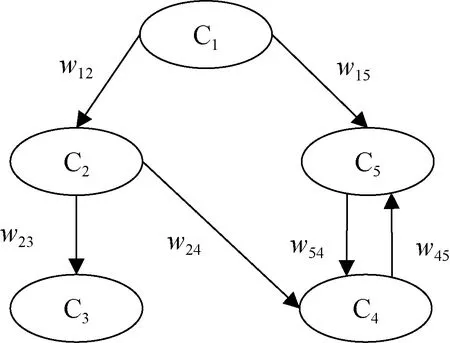
图2 模糊认知图结构示意图Fig.2.Schematic diagram of FCM structure
(2)FCM 的数学表示与推理机制
FCM 基本模型以简单的四元组G=(C,X,W,f)进行数学表示,其中,由n个概念节点组成的集合C={C1,C2,…,Cn};概念节点C1至Cn在某一时刻的状态值组成的集合X={x1,x2,…,xn};任意两个概念节点Ci对Cj的有向弧权值所构成的集合W={wij},则W={wij}n×n即为整个FCM 模型的邻接矩阵;f代表阈值函数,其目的是将每次迭代后的节点状态值转化为[-1,1]。每个节点在不同时间点的状态值不同,若在时间点t时,n个概念节点组成的状态值集合X(t)={x1(t),x2(t),…,xn(t)},那么在时间点t+1 时,n个概念节点的状态值即为:
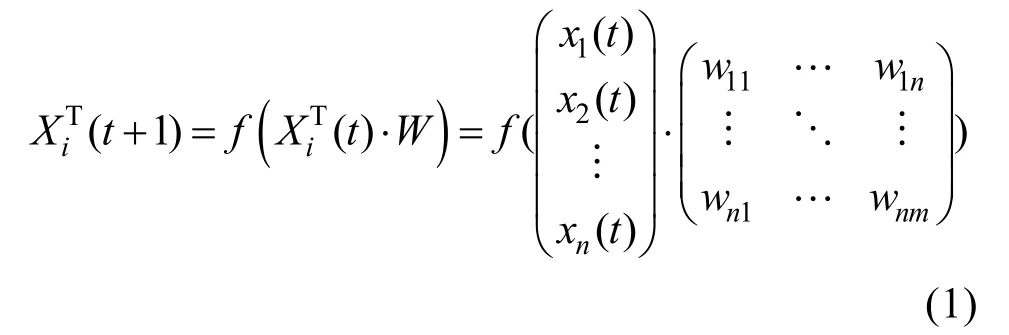
常见的阈值函数有双曲正切函数,Sigmoid 函数。根据模糊特征,选择陡度参数λ的Sigmoid函数为阈值函数:
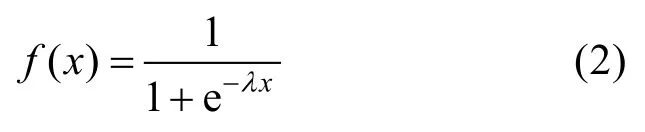
对概念节点的状态值进行迭代计算后,将最终稳定至一个固定点或极限循环两种状态。但实际上,FCM 推理也可能会使各个节点进入无限不循环状态,即为一种混沌状态。
3.2 模糊认知图分析法有向弧权值:模糊层次分析法
FCM 因果关系形成后,对存在因果关系的两个概念节点间的有向弧权重做进一步分析。文章引入梯形模糊数法及专家置信度水平来进行模糊综合评估[69]。首先收集并量化专家评语。邀请海上交通安全领域北极安全领域内共5 位专家并展开问卷调查,将调查结果转化为梯形模糊数A=(a1,a2,a3,a4)(表5)。其次,计算专家置信度。受异质专家的个人阅历知识背景行业经验的影响,专家评语往往不可一概而论。引入专家置信度(专家权重)概念,从职位水平(epl)学历水平(edl)经验水平(eel)和适任水平(ecl)来确定专家综合置信程度,评分标准见表6。专家评语置信度(el)以及专家置信度Q(Eu)的计算公式分别为:
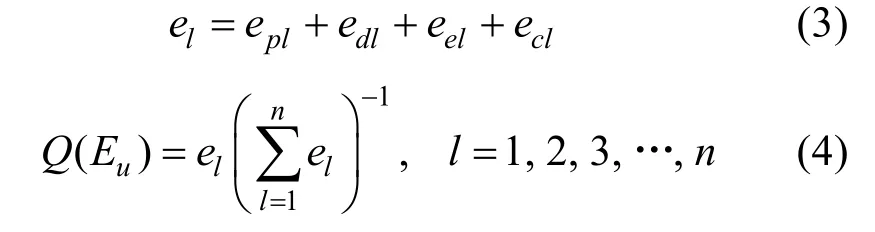

表5 专家评语标度Table 5.Expert comment scale

表6 专家置信度评分标准Table 6.Expert confidence scoring standards
第m位专家评语为Pm(m=1,2,…,n),分别计算专家评语的平均一致度和一致性系数并进行去模糊化处理,测量有向弧权重。
第1 步,评语间相似度计算:若以Pu(a1,a2,a3,a4)和Pv(b1,b2,b3,b4)表示两位专家评语的梯形模糊数标度,那么两位专家间评语相似度Suv(Pu,Pv)表示为:
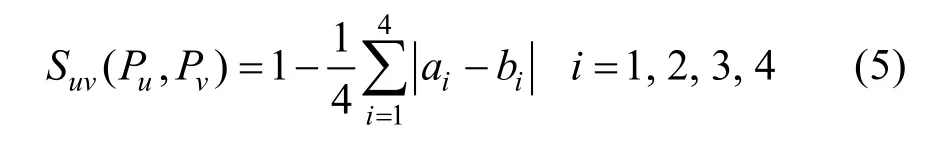
第2 步,平均一致度计算:若有n位专家,第u位专家评语平均一致度AA(Pu)表示为:
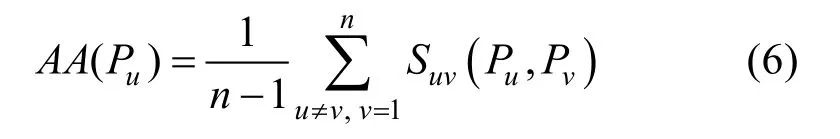
第3 步,相对一致度计算:若有n位专家,第u位专家评语相对一致度RA(Pu)表示为:
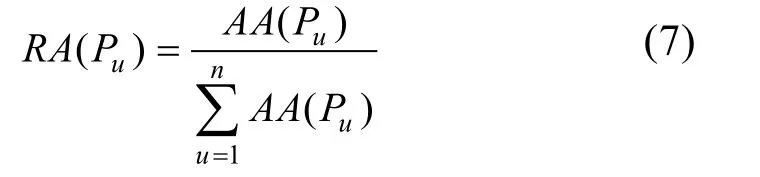
第4 步,一致性系数计算:Q(Eu)对于RA(Pu)的重要程度以β表示,β取0.5,第u位专家的一致性系数CC(Pu)表示为:
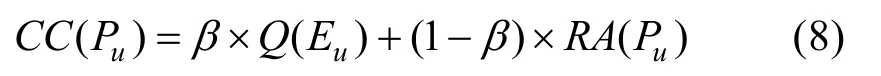
第5 步,聚类模糊数计算:聚类模糊数以RA表示为:
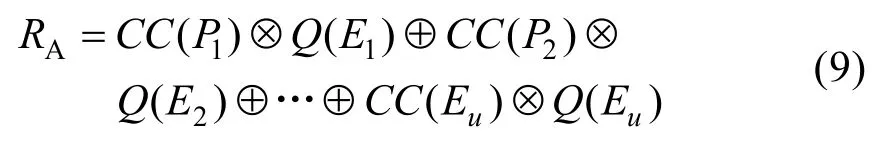
第6 步,去模糊化处理:采用中心面积法去模糊化,以μM(x)表示聚合的隶属函数,去模糊化权重以AV表示为:
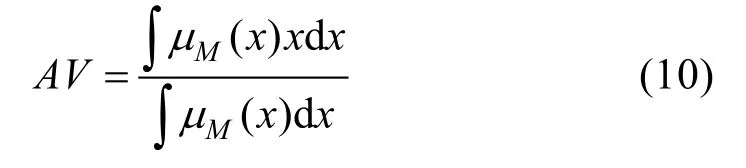
当模糊综合评价集采用梯形模糊数标度时,若梯形模糊数为A=(a1,a2,a3,a4),则有:
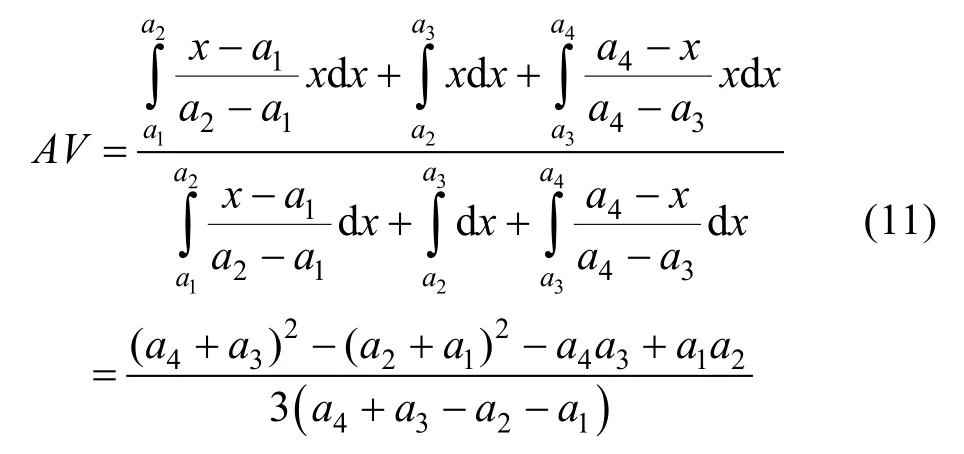
4 韧性视域下北极航行风险级联效应分析
4.1 风险指标判断标准与情景选定
根据前文分析可知,风险存在两种表现形式,当风险状态未达到既定阈值时,风险仅可被视作具有潜在危险性的“风险要素”;当风险达到甚至超过既定阈值时,风险由潜在危险状态转变为具有现实损失的破坏性“风险事件”。因此,确定阈值以判断风险表现至关重要。在综合国内外北极航线风险等级界定标准以及广泛征询专家意见的基础上,结合前期研究成果以及研究区域背景状况,针对定量客观指标,即本质性风险,构建判断层来界定风险要素及其量值范围(表7)。对于定性指标,即诱致性风险,由于指标自身具有一定的笼统性和不确定性,很难以统一的标准来界定其量值范围,因此诱致性风险量值范围主要通过领域内专家和具有北极航行经验船员的打分结果获得。表7 为获取北极航行风险因果关系强度以及级联效应情景模拟分析提供了重要的指示性参考。
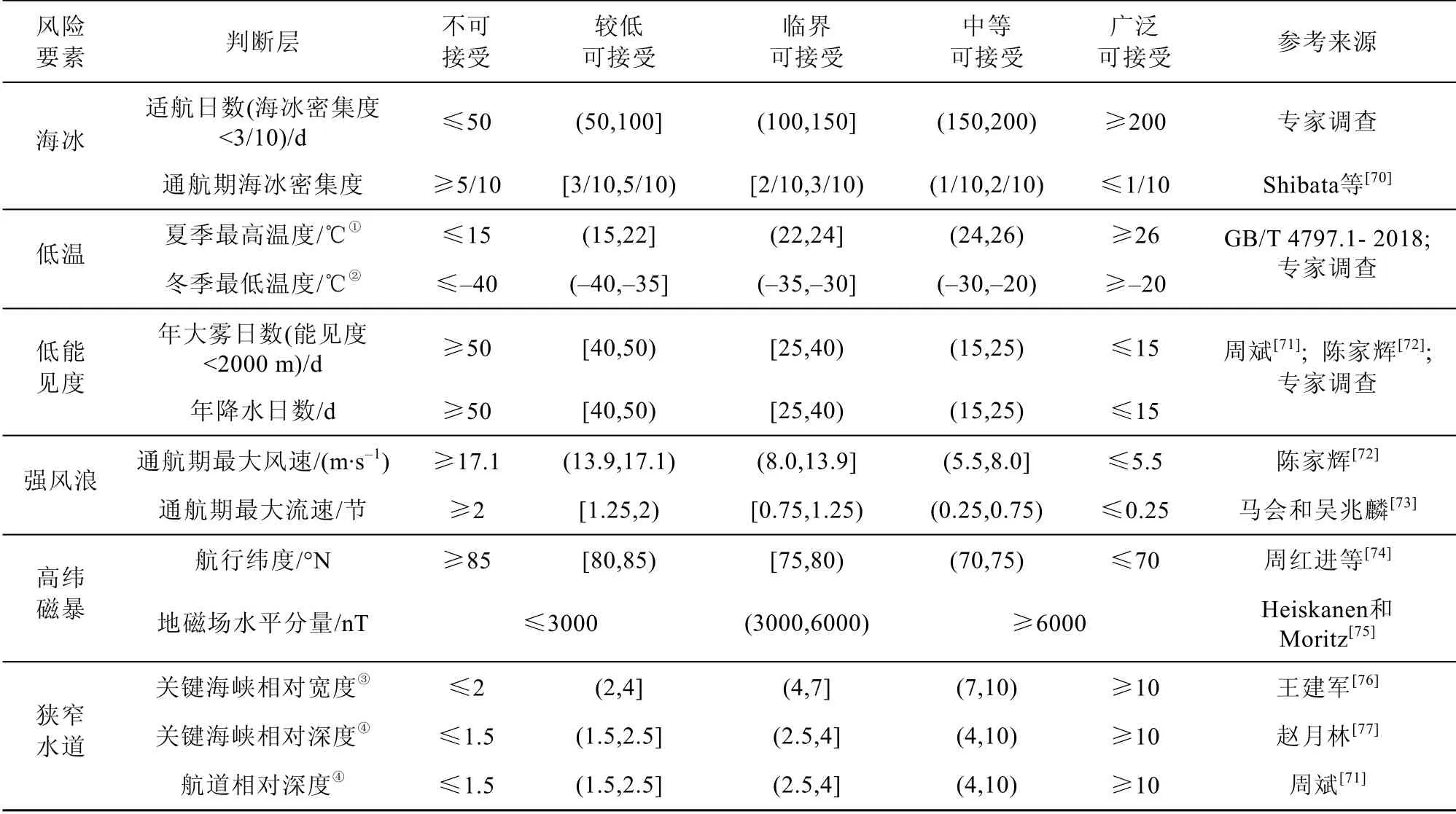
表7 北极航行本质性安全风险指标判断标准及参考来源Table 7.Judgement standards for essential risk of Arctic navigation and reference sources
通过文献分析与专家意见收集,确定当风险节点中的任意一个判断层指标达到“较低可接受”水平时,风险节点便处于激活状态。处于激活状态的风险节点具备两种能力,一是能够对系统产生干扰,二是能够促使与其相关的因果关系链活跃起来,进而产生风险级联。从北极客观环境出发,以表8 收集到的事故报告分析为基础,将“海冰”“低温”两个本质性风险确定为北极航行常态化风险要素,将“船员适任性低”及“国际交流渠道狭窄”两个诱致性风险确定为高频风险要素。以此为例分别开展本质性风险级联效应情景分析以及诱致性风险级联效应情景分析。

表8 底层数据统计信息及其来源Table 8.The underlying data statistics and their sources
4.2 北极航行风险FCM 模型构建
根据表4 北极航行风险因果关系,构建由一级指标间一级与二级指标间以及二级指标间的联合模糊认知图模型(图3)。

图3 韧性视域下北极航行风险的模糊认知图Fig.3.A fuzzy cognition map of Arctic navigation risks from the perspective of resilience
4.3 北极航行风险因果关联程度分析
为保证研究结果科学可靠,以表7 和表8 为指示性参考,选择北极安全海上交通安全领域内的科研专家和有经验的船员组成异质专家组展开讨论与调查。根据表6 及公式(3)(4)对每位专家的置信度进行计算,专家信息及置信度水平见表9。

表9 专家信息及置信度水平Table 9.Expert information and the confidence level
根据公式(5)~(11)计算存在因果关系的有向弧权值,三类因果关系的有向弧权值测量结果见表10。
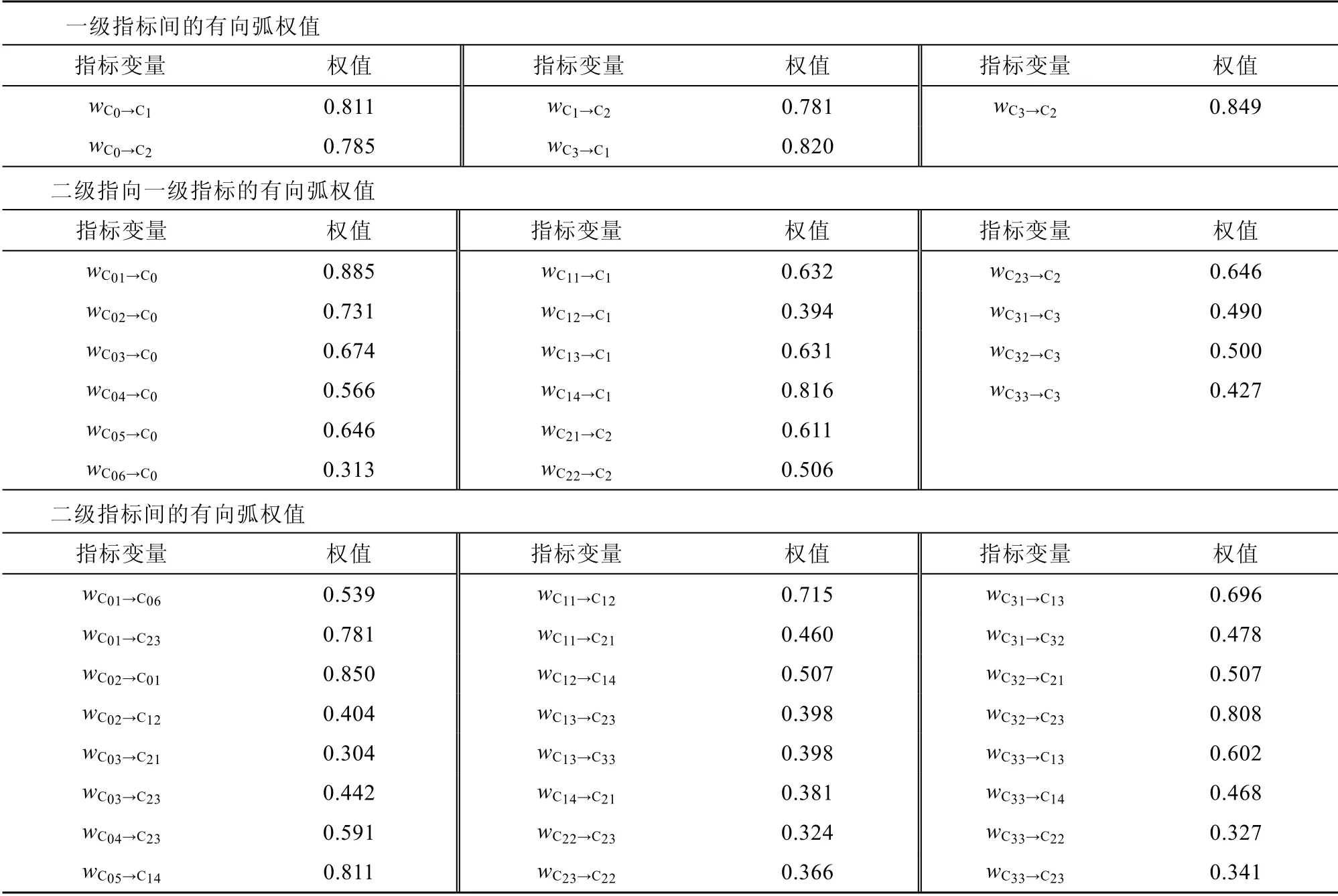
表10 FCM 有向弧权值Table 10.FCM directed arc weights
本研究共确定了45 条有向弧权值,其中,一级指标间,C3→C2的因果关系最强,有向弧权值达到0.849;C3→C1的因果关系次之,有向弧权值达到0.820,表明在一般情况下,“宏观性风险”对导致“常规性风险”与“变例性风险”具有很强的效果。一级与二级指标间,C01→C0的因果关系最强,有向弧权值达到0.885,表明在一般情况下“海冰”对导致“本质性风险”水平的提高具有很强的效果;C14→C1的因果关系次之,有向弧权值为0.816,表明在一般情况下,“导助航设备失灵”对导致“常规性风险”水平的提高具有很强的效果。二级指标间,C02→C01的因果关系最强,有向弧权值达到0.850,表明在一般情况下“低温”对导致“海冰”具有很强的效果,C05→C14的因果关系次之,有向弧权值为0.811,表明在一般情况下“高纬和磁暴”对导致“导助航设备失灵”具有很强的效果。
4.4 情景一:北极航行本质性风险的级联效应分析
激活模糊认知图中特定节点开展情景模拟分析。激活特定风险节点后,经过多次迭代,如果模型中其他风险节点的状态值不再发生明显变化,符合收敛性要求,则表明该情景具有现实意义,此时,所有节点的最终状态值与初始状态值之间的差值表征该节点与激活风险节点之间的级联强弱[80]。如果多次迭代后,其他风险节点状态值无法收敛,表明激活的风险节点与其他任何风险节点间不存在明显的级联关系。以本质性风险中的“海冰C01”和“低温C02”作激活风险节点为例,风险的级联效应分析过程为:
(1)第一阶段:以C01C02为激活节点
第1 步,定义初始向量,赋予初始向量状态值:20 个概念节点组成的初始状态值集合X(0)={1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0}。
第2 步,递推下一时刻状态值,迭代状态值:根据公式(1)得出下一时刻状态值。
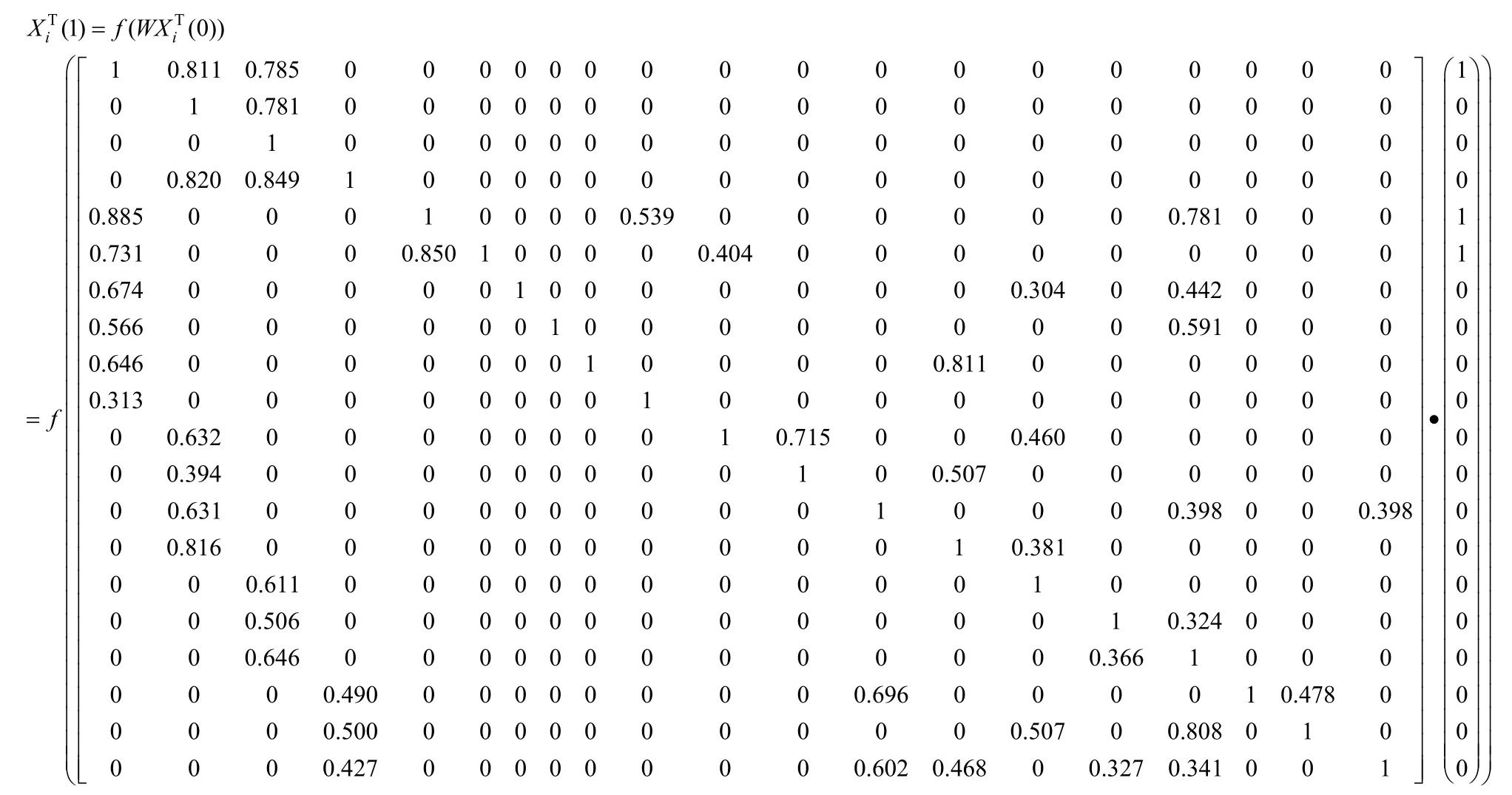
根据公式(2)代入变换函数,其中λ取5,则有:

第3 步,校准状态向量:满足X(t)=X(t+ 1),则迭代结束,X(t+ 1)为最终状态向量值。显然X(1)≠X(0),即X(1)不是模型最终状态向量值,需要继续迭代计算。
第4 步,多次迭代直至状态值稳定:在本情境下,经过13 次迭代计算,得到X(12)=X(13),即X(13)为最终状态向量值。部分迭代次数状态向量值及数值变化幅度M(Ci)如表11所示,其中Is表示第s次迭代。

表11 部分时刻各节点状态向量值及数值变化幅度(情景一:第一阶段)Table 11.The state vector value and numerical change range of each node at some time(scenario 1:first stage)
在推理的过程中,激活节点以外的其他节点状态值均发生了变化,表明其他风险节点均与“海冰”和“低温”存在一定的级联关系。M(Ci)表示第i个节点初始状态值与收敛状态值之间的差值,数值越小,表明该节点与激活风险节点的级联性越强。按照M(Ci)由小到大依次是“获援概率极低C23”(0.0197)“狭窄水道C06”(0.0629)“维护保养不到位 C12”(0.1173),其他节点的M(Ci)均在0.49 附近,这说明在“海冰”“低温”风险环境下,最容易导致的风险事件依次是“获援概率极低”“狭窄水道”“维护保养不到位”。那么在下一阶段的情景模拟过程中,激活节点便由2 个扩大到5 个。
(2)第二阶段:以C01C02C06C12C23为激活节点
以“海冰”“低温”“狭窄水道”“维护保养不到位”“获援概率极低”驱动模糊认知图模型,重复第一阶段的第1~4 步,观察M(Ci),结果如表12所示。
根据表12,经过第二阶段的推理发现,以源激活节点(“海冰”“低温”)及一次级联节点(“维护保养不到位”“获援概率极低”“狭窄水道”)为新的激活节点驱动模糊认知图模型,除了一次级联节点M(Ci)较第一阶段明显变小以外,按照M(Ci)由小到大依次是“导助航设备失灵 C14”(0.0733)“设备抢修速度慢C22”(0.1379),其他节点M(Ci)均在0.49 附近。这说明在该情景下,当风险事件递进至第二阶段时,最容易导致的风险事件依次是“导助航设备失灵”“设备抢修速度慢”。
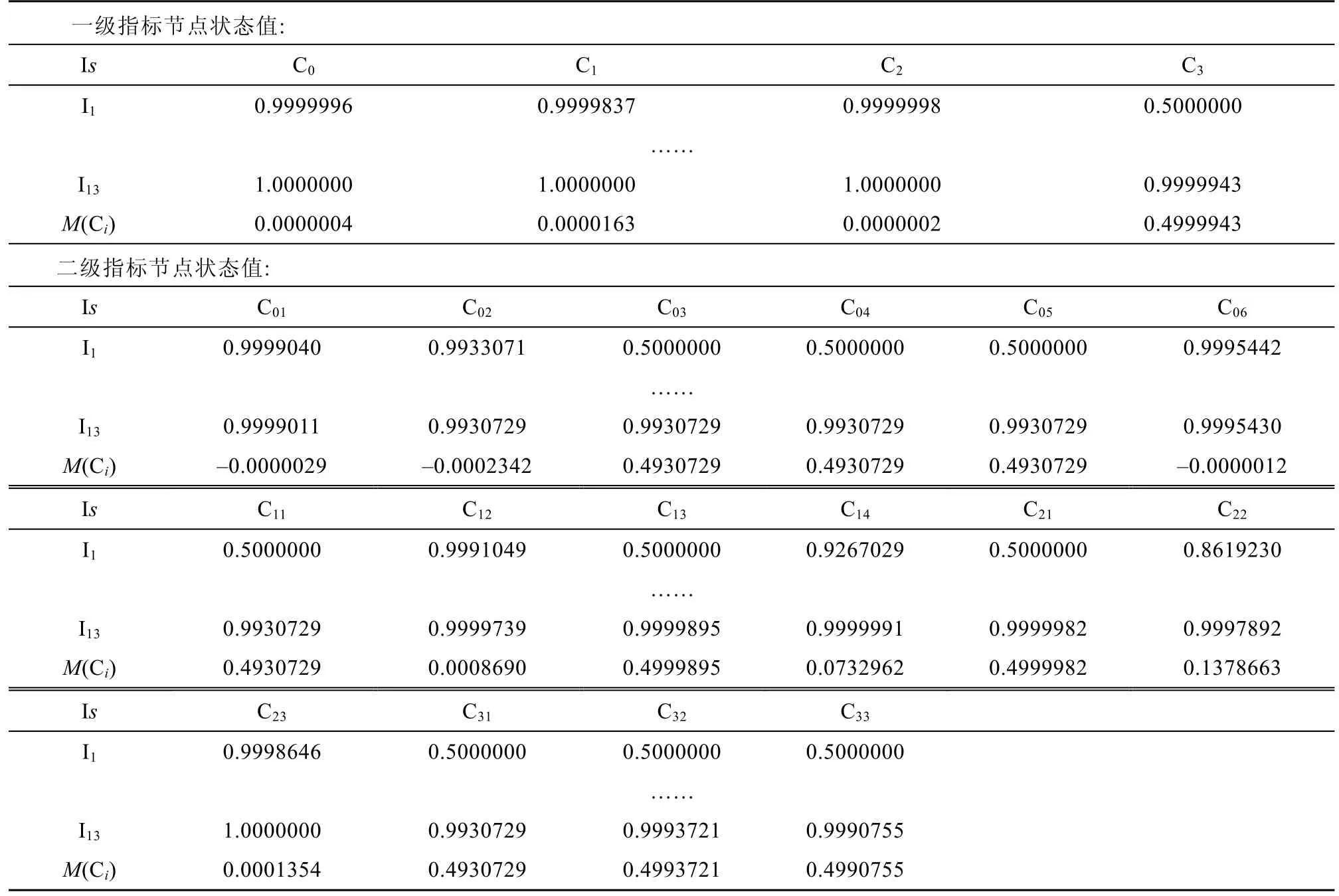
表12 部分时刻各节点状态向量值及数值变化幅度(情景一:第二阶段)Table 12.The state vector value and numerical change range of each node at some time(scenario 1:second stage)
(3)第三阶段:以C01C02C06C12C14C22C23为激活节点
以“海冰”“低温”“狭窄水道”“维护保养不到位”“导助航设备失灵”“设备抢修速度慢”“获援概率极低”驱动模糊认知图模型,重复第一阶段的第1~4 步,观察M(Ci),结果如表13所示。
根据表13,经过第三阶段的推理发现,以源激活节点(“海冰”“低温”)一次级联节点(“维护保养不到位”“获援概率极低”“狭窄水道”)及二次级联节点(“导助航设备失灵”“设备抢修速度慢”)为新的激活节点驱动模糊认知图模型,除了二次级联节点M(Ci)较第一阶段明显变小以外,只有“疏散调度能力弱C21”对应的M(Ci)明显变小,为0.1296。这说明在该情景下,当风险事件递进至第三阶段,最容易导致的风险事件是“疏散调度能力弱”。
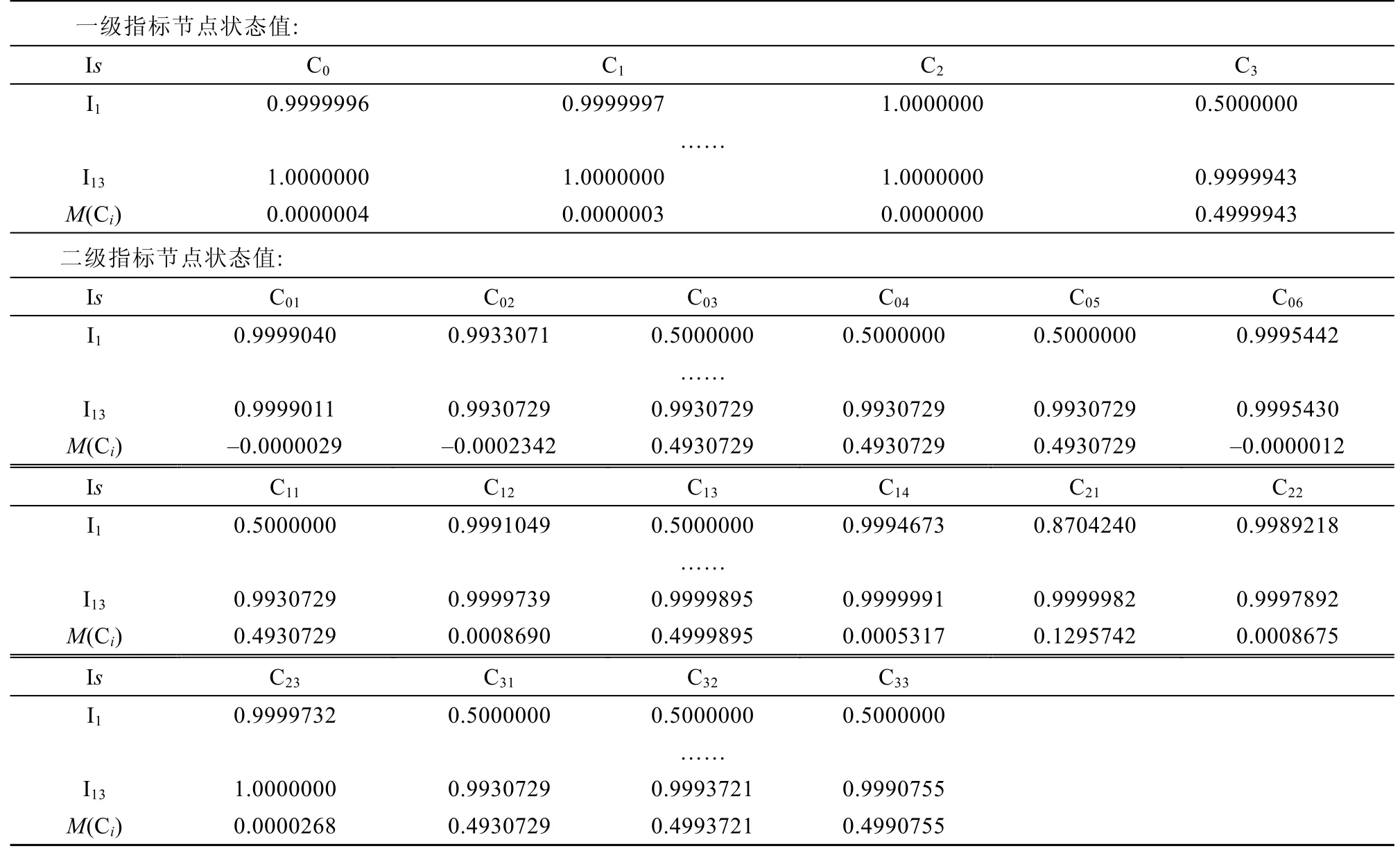
表13 部分时刻各节点状态向量值及数值变化幅度(情景一:第三阶段)Table 13.The state vector value and numerical change range of each node at some time(scenario 1:third stage)
(4)第四阶段:以C01C02C06C12C14C21C22C23为激活节点
以“海冰”“低温”“狭窄水道”“维护保养不到位”“导助航设备失灵”“疏散调度能力弱”“设备抢修速度慢”“获援概率极低”驱动模糊认知图模型,重复第一阶段的第1~4 步,观察M(Ci),结果如表14所示。
根据表 14,经过第四阶段的推理发现,以源激活节点(“海冰”“低温”)一次级联节点(“维护保养不到位”“获援概率极低”“狭窄水道”)二次级联节点(“导助航设备失灵”“设备抢修速度慢”)及三次级联节点(“疏散调度能力弱”)为新的激活节点驱动模糊认知图模型,除了三次级联节点的M(Ci)较第二阶段明显变小以外,其余节点M(Ci)均没有发现明显的变化,即没有导致新的风险发生。则以“海冰”“低温”为源激活节点的风险级联过程情景模拟结束。
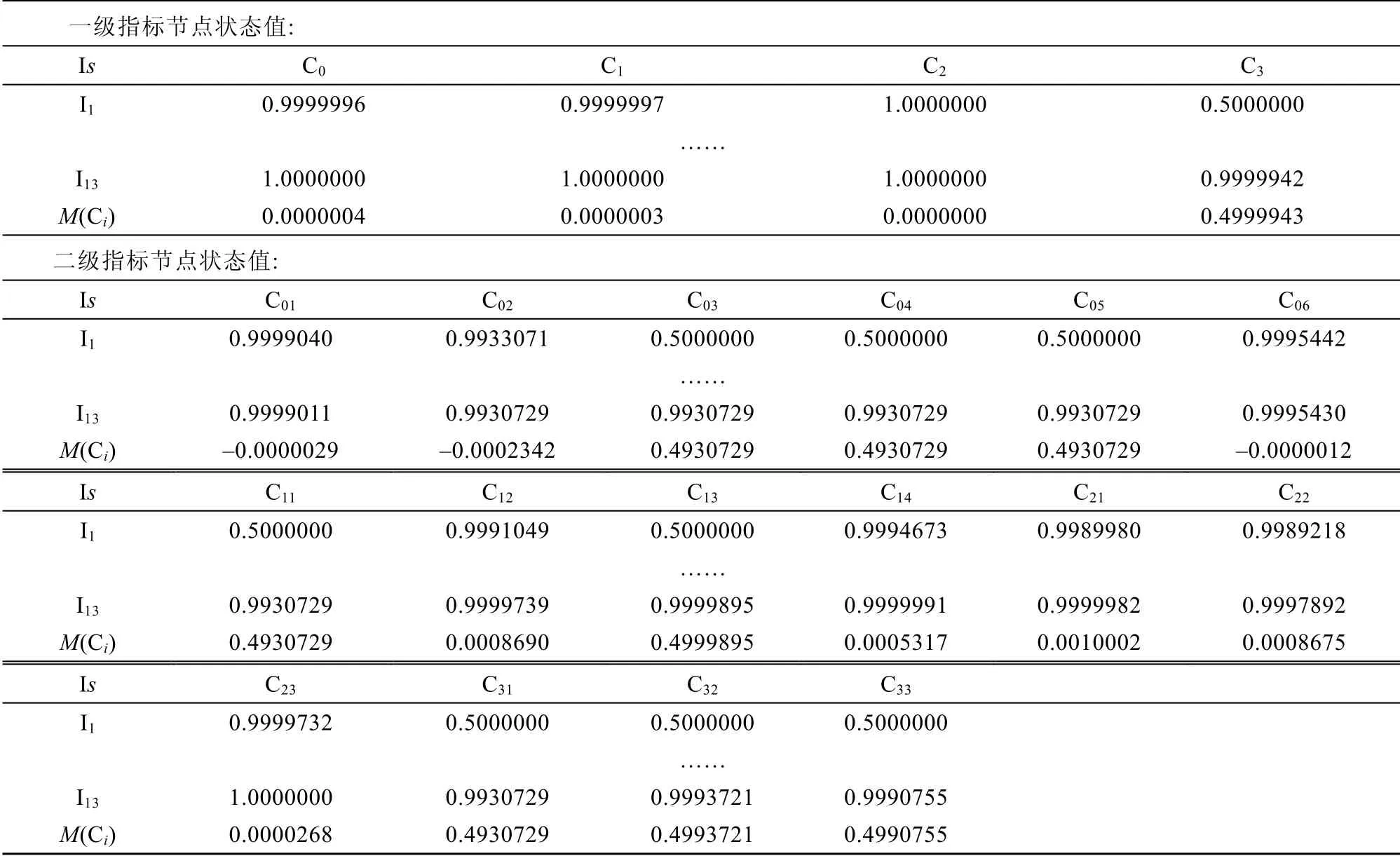
表14 部分时刻各节点状态向量值及数值变化幅度(情景一:第四阶段)Table 14.The state vector value and numerical change range of each node at some time(scenario 1:fourth stage)
4.5 情景二:北极航行诱致性风险的级联效应分析
“海冰C01”与“低温C02”是北极航行常态化风险要素,在分析诱致性风险级联效应过程中也应处于激活状态。在分析表8 中相关事故报告
的基础上,选取“船员适任性低C11”“国际交流渠道狭窄C31”两个诱致性风险要素作为激活节点,开展风险级联效应分析工作,计算过程同第4.4 节。
(1)第一阶段:以C01C02C11C31为激活节点
以“海冰”“低温”“船员适任性低”“国际交流渠道狭窄”为激活节点驱动模糊认知图模型,重复4.4 节的第1~4 步,观察M(Ci),结果如表15所示。
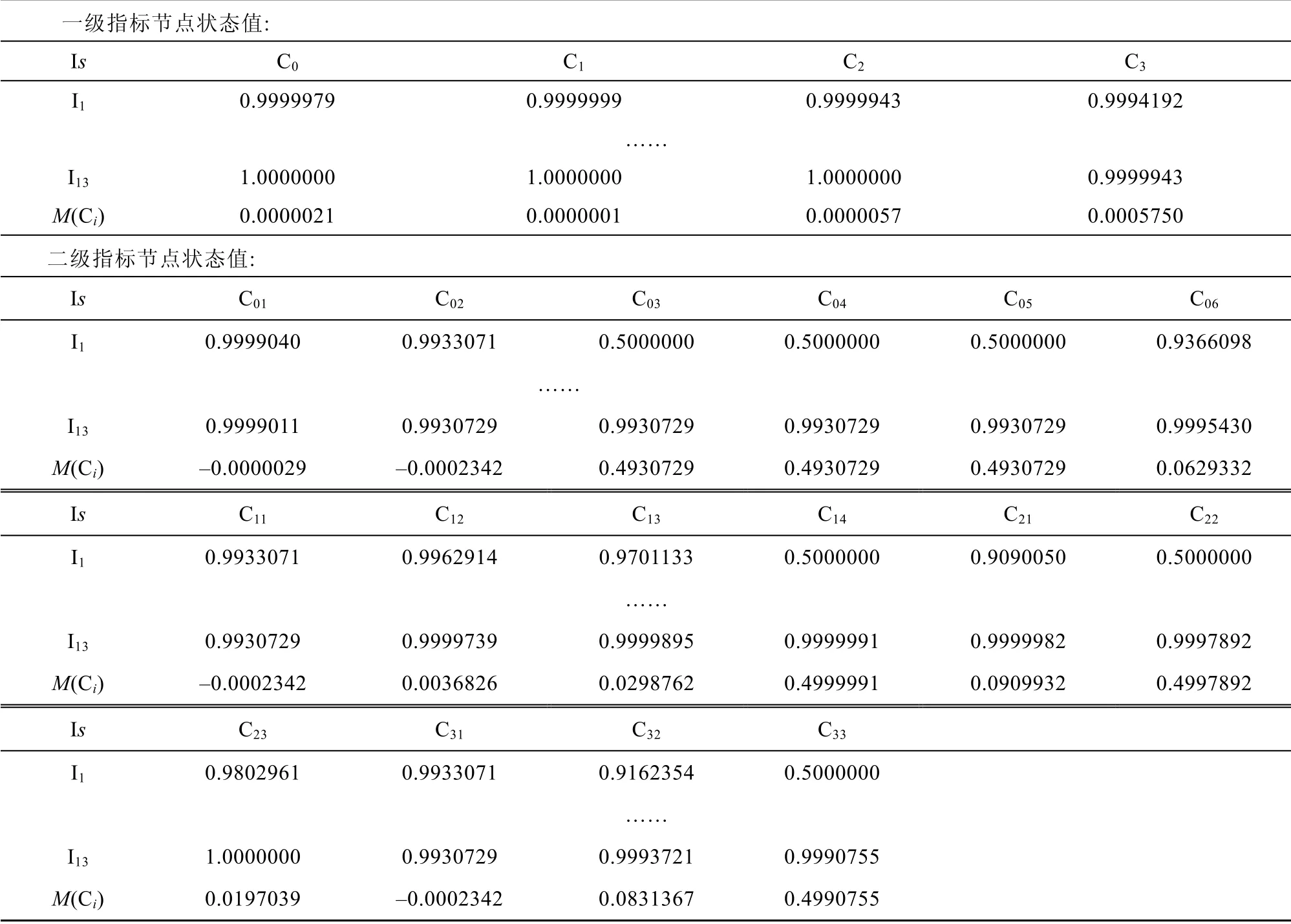
表15 部分时刻各节点状态向量值及数值变化幅度(情景二:第一阶段)Table 15.The state vector value and numerical change range of each node at some time(scenario 2:first stage)
根据表15,经过第一阶段的推理发现,每个风险节点的状态值均有所不同,表明以C01C02C11C31为激活风险驱动模糊认知图展开情景模拟具有现实意义。按照M(Ci)由小到大依次是“维护保养不到位C12”(0.0037)“获援概率极低C23”(0.0197)“北极航行资料缺失C13”(0.0299)“狭窄水道C06”(0.0629)“北极救援力量匮乏C32”(0.0831)及“疏散调度能力弱C21”(0.0910),其他节点M(Ci)均在0.49 附近。这说明在常态化风险环境下(海冰和低温),“船员适任性低”以及“国际交流渠道狭窄”形成的风险组合最容易导致的风险事件依次是“维护保养不到位”“获援概率极低”“北极航行资料缺失”“狭窄水道”“北极救援力量匮乏”及“疏散调度能力弱”。
(2)第二阶段:以C01C02C06C11C12C13C21C23C31C32为激活节点
以“海冰”“低温”“狭窄水道”“船员适任性低”“维护保养不到位”“北极航行资料缺失”“疏散调度能力弱”“获援概率极低”“国际交流渠道狭窄”“北极救援力量匮乏”为激活节点驱动模糊认知图模型,重复4.4 节中第1~4步,观察M(Ci),结果如表16所示。
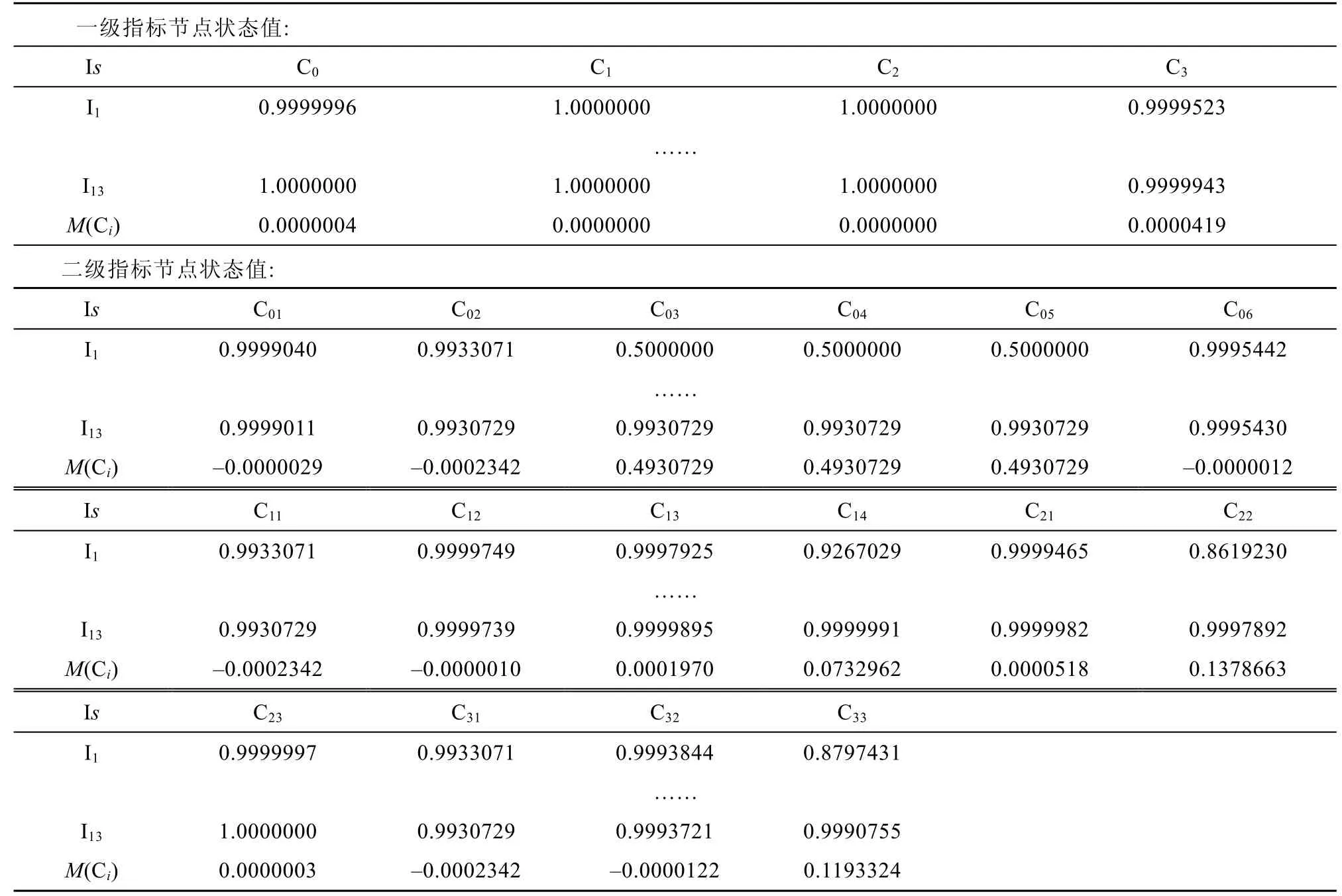
表16 部分时刻各节点状态向量值及数值变化幅度(情景二:第二阶段)Table 16.The state vector value and numerical change range of each node at some time(scenario 2:second stage)
根据表16,经过第二阶段的推理发现,以源激活节点(“海冰”“低温”“船员适任性低”“国际交流渠道狭窄”)及一次级联节点(“维护保养不到位”“获援概率极低”“北极航行资料缺失”“狭窄水道”“北极救援力量匮乏”及“疏散调度能力弱”)为新的激活节点驱动模糊认知图模型,除了一次级联节点的M(Ci)较第一阶段明显变小以外,按照M(Ci)由小到大依次是“导助航设备失灵C14”(0.0733)“科考及技术创新不足C33”(0.1193)“设备抢修速度慢C22”(0.1379)。这说明在该情景下,当风险递进至第二阶段,最容易导致的风险事件依次是“导助航设备失灵”“科考及技术创新不足”“设备抢修速度慢”。同时,可以发现,当风险状况递进至该阶段时,除了部分本质性风险M(Ci)没有明显变化外,其他风险均被激活,表明诱致性风险相对于本质性风险在风险级联过程中的连锁效应更迅速也更为猛烈。由于各个节点均被激活,在此情景下,风险级联效应模拟过程结束。
4.6 结果解析与方法评析
根据模拟过程,做出如下分析。
以“海冰”“低温”为源激活节点开展北极航行风险级联效应的情景模拟结果显示:风险级联效应共经历了四个阶段,最容易导致“获援概率极低”“狭窄水道”“维护保养不到位”。整体来看,级联过程激活的6 个风险节点均对应韧性理论下的吸收和适应能力。因此,未来北极航行安全保障基础能力建设过程中应重点发展风险的吸收和适应能力。
以“海冰”“低温”“船员适任性低”“国际交流渠道狭窄”为源激活节点开展北极航行风险级联效应的情景模拟结果显示:风险级联效应共经历了两个阶段,最容易导致“维护保养不到位”“获援概率极低”“北极航行资料缺失”。整体来看,级联过程中,诱致性风险下的全部节点均被激活。因此,在诱致性风险主动发挥作用时,北极航行安全保障基础能力建设过程中应同时关注风险的吸收适应和变革能力。
北极水域环境复杂多变,脆弱敏感,非传统性安全风险越来越成为北极航行风险研究的关注重点[31]。从风险识别到风险评价,再到风险控制,北极航行风险管理研究逐步体系化。传统视角下的北极航行风险要素识别主要集中于两大方面:一方面,基于“人-机-环-管”的北极航行风险分析成为主流框架[81],其中也有对四大维度中某一要素(如海冰[82]磁场[74]等)的细化研究;另一方面,依托碰撞或搁浅事故展开的风险分析模式也较为常见[27,83]。其次,在分析方法方面,除了有贝叶斯网络[5]事故树[84]神经网络[49]等定量分析模型的引入以外,也有基于理论层面的定性探讨[85]。从传统分析方法取得的结论来看,譬如:有借助加权综合评价展开北极东北航道风险区划分析,得出了海冰风速对北极安全航行影响较大的结论[86];有依托模糊层次分析法从经济技术政治安全几个角度对北极航道综合性风险进行排序[87],证明了航行安全和地缘政治领域的风险点对北极航行有重要的影响;同时也有基于“马尔科夫链-蒙特卡洛方法”构建了云模型,得出北极航行风险随时间变化波动明显的结论[88]。从研究方法到研究结果,总结来看,依托于传统风险分析方法所得出的研究结论主要集中于两个方面,一是能够识别出北极航行关键风险要素,二是证实了风险要素间存在着动态变化过程。所以,将以上两个研究议题结合起来,深入探讨关键风险要素之间的互动关联,模拟(还原)这种动态变化过程,为突破风险困境提出保障能力建设策略显得更加重要。这是目前国内外学者较少关注的问题。因此,突破现有对于风险要素识别及其自身影响效果分析的研究界限,基于韧性理论,依托模糊认知图模型,模拟了两种情景下的风险级联过程。与现有研究方法取得的结果不同,该方法能够明晰北极航行风险级联效应究竟如何放大,明确风险之间的关联传递过程。同时,更为重要的一点是,所采用的“风险-韧性”框架能够直接从量化结果中明确北极航行安全保障能力建设的着力点,这实际上摆脱了先问题分析,后对策建议,将两者割裂来看的研究范式,实现了“问题”与“对策”融合,这也恰恰体现了“风险”与“韧性”的内在逻辑与韧性理论研究优势。
5 结论
北极航行风险具有模糊多变的特征,传统风险分析范式的研究视角始终困囿于“由外而内”“风险控制”“消极被动”的层面。因此,在现实与技术的矛盾下,应对北极航行风险很难摆脱左支右绌的困境。韧性理论框架下的北极航行风险研究实现了“由内到外”“由‘风险控制’到‘风险适应’”“由‘消极被动’到‘积极主动’”的姿态转变,即在承认北极航行风险模糊复杂可变敏感的前提下,应该如何从安全主体角度出发来看待和控制北极航行风险。在该理论的指引下展开风险指标识别,将“韧性”与“级联效应”结合,首次探讨了北极航行风险的级联效应,改变了传统分析方法集中于北极航行风险的表面性研究,真正将风险串联起来。另外,将模糊认知图分析法引入北极航行风险分析中来,为风险理论中的级联效应研究提供了量化分析路径。
本研究基于韧性理论的三个能力要素(吸收适应变革)提出了一个以韧性视角来认知北极航行风险(本质性常规性变例性宏观性)的研究范式,并以此为切入点对北极船舶航行安全风险级联效应做深入分析。引入梯形模糊数和模糊层次分析法来量化各风险节点间的因果关系强度,构建了可用于韧性视域下北极航行安全风险分析的模糊认知图,为采取模拟实体方法研究北极航行安全风险提供了通用模型。最后针对两种风险情景,通过级联效应分析,模拟风险级联过程,指出为获取持续安全状态所应当重点关注的韧性能力。研究表明:北极常态化风险环境(海冰和低温)下,风险级联效应共产生四个阶段,最容易导致“获援概率极低”“狭窄水道”“维护保养不到位”等,此情景下应重点关注风险的吸收和适应能力;在常态化风险环境耦合“船员适任性低”和“国际交流渠道狭窄”两个诱致性风险的情景下,风险级联效应共产生两个阶段,最容易导致“维护保养不到位”“获援概率极低”“北极航行资料缺失”等,此种情景风险级联效应的过程更为迅速和猛烈,应同时兼顾风险的吸收适应和变革能力。
—— “T”级联

