强迫振动下拉索-MR阻尼器系统半主动控制仿真研究

刘江云

摘 要：为了验证MR阻尼器在强迫振动下对拉索进行半主动控制的效果，本研究采用RD-1005-03型MR阻尼器，以通用設计曲线为基础，并基于Simulink系统编制半主动控制算法程序框图，实现正弦荷载强迫振动下的拉索MR阻尼器系统的半主动控制仿真。根据所提出的半主动控制算法，计算拉索-MR阻尼器系统的动力响应。最后，结合各测点处加速度的均方根值，评价半主动控制的效果。

关键词：MR阻尼器;半主动控制;正弦激励

中图分类号：U448     文献标志码：A     文章编号：1003-5168（2022）10-0038-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.10.008

Simulation Study on Semi-Active Control of Cable MR Damper System Under Forced vibration

LIU Jiangyun

（Wuhan University， Wuhan 430212，China）

Abstract： In order to verify the semi-active control effect of MR damper on cable under forced vibration， rd-1005-03 MR damper is used in this study. Based on the general design curve and Simulink system， the program block diagram of semi-active control algorithm is compiled to realize the semi-active control simulation of cable MR damper system under sinusoidal load forced vibration. According to the proposed semi-active control algorithm， the dynamic response of cable MR damper system is calculated.Finally， combined with the root mean square value of acceleration at each measuring point， the effect of semi-active control is evaluated.

Keywords： MR damper;semi active control;sinusoidal excitation

0 引言

随着城市建设的不断发展，建筑的跨度不断增大，越来越多的体育场馆、展览馆、购物中心等大型公用建筑开始使用拉索结构，因拉索本身阻尼较小，且质量轻、刚度小，这使得拉索易在各种作用下发生振动时振型复杂且幅度较大，因此有效的减振措施显得尤为重要[1]。在拉索锚固端附近安装被动阻尼器是最为常见的一种减振措施，阻尼器的安装高度受到美观及使用功能要求等的限制，一般被动阻尼器无法满足长拉索的减振要求。

Dyke等[1]针对MR阻尼器减振效果的试验，得出了半主动控制效果远好于被动控制的结论。Liu等[2]对采用MR阻尼器的拉索缩尺模型进行了振动控制研究，验证了半主动 MR阻尼器的减振效果明显优于被动阻尼器。

本研究以武汉某购物中心穹顶拉索为例，采用RD-1005-03型MR阻尼器，基于双线性力学模型，建立拉索-MR阻尼器控制模型，提出以通用设计曲线为基础的拉索半主动控制算法，运用数值模拟正弦荷载强迫振动，验证MR阻尼器的半主动控制效果。

1 MR阻尼器半主动控制算法

假设忽略拉索垂度、倾角、弯曲刚度等的影响，对于一般的拉索-阻尼器系统（见图1）可建立张紧弦动力学方程，如式（1）。

[mv（x，t）+cv（x，t）-Tv"（x，t）=f（x，t）+Fd（t）δ（x-xd）]    （1）

式中：T为拉索张拉力;m为拉索单位长度质量;c为拉索单位长度固有阻尼;v（x，t）为拉索位移，[v]（x，t）及[v]（x，t）分别为对应的速度以及加速度;v"（x，t）为某点某时刻的位移对x的二次导数;f（x，t）为施加在拉索上任意长度的均布荷载;Fd（t）为阻尼器处阻尼力;[δ（x-xd）]为[δ-dirac]函数。

将式（1）用模态位移和型函数的形式表达，并通过标准Galerkin法进行变换得出式（2）。

[Mq+Cq+Kq=fq+φ（xd）Fd（t）q]  （2）

式中：[q]为模态位移矩阵;[φ（xd）]为模态形函数矩阵;[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;[fq]为荷载矩阵;[Fd（t）]为阻尼力;[xd]是自锚固点算起的阻尼器安装长度。

模态形函数有多种取法，这里选用Pacheco等[3]等提出的正弦函数形式，见式（3）。

[φj（x）=sin（jπx/L）]     （3）

式中：[L]是拉索长度;[j]为模态阶数。

这样就可以将动力学方程解耦，得到全是对角阵的系数矩阵，如式（4）至（6）。

[M=diagmii，mii=mL2]    （4）

[C=diagcii，cii=cL2]    （5）

[K=diagkii，kii=Tπ2i22L]    （6）

并將动力学方程转化为以下状态方程，如式（7）。

[Z（t）=（A-GL）Z（t）+Bfq（t）]  （7）

其中：

[Z=qq]   [A=0                   I-M-1K        -M-1C]

[G=0M-1φ（xd） ][  B=0M-1] [  L=0    Cd，optφT（xd）]

式中：Cd，opt表示MR阻尼器等效线性最优阻尼系数，可以通过Krenk[4]提出的线性阻尼器通用设计曲线近似求得，见式（8）。

[Cd，opt=mL2ω01i·xd·π2]      （8）

式中：[ω01]是拉索一阶圆频率，[i]为主振型模态。

蒋小路[5]对Lord公司生产的型号为RD-1005-03的MR阻尼器进行了阻尼器单体试验，得到了阻尼器等效阻尼和电流的双线性关系，见式（9）。

[C=（c1+f1Vmax）I+（c2+f2Vmax），0≤I≤0.5 A（c3+f3Vmax）I+（c4+f4Vmax），0.5A≤I≤2 A]

（9）

式中：[C]为阻尼器等效阻尼;[I]为阻尼器输入电流;[Vmax]为阻尼器最大速度。其他参数详见表1。将由式（8）得到的最优阻尼系数代入双线性关系可以得到最优电流，将最优电流输入阻尼器即可产生最优控制力，达到半主动控制效果。

根据上述半主动控制算法，可以建立如图2所示的拉索-MR阻尼器系统半主动控制流程。

2 数值模拟

本研究以武汉某购物中心一根长为95 m的拉索为例，对其进行半主动控制仿真，拉索具体参数见表2。

仿真简谐荷载形式为式（10）。

[f（x，t）=Asin（2πft）]    （10）

式中：A为幅值，本研究取800。

将拉索分为k（本例为95）段，共有k+1（本例为96）个节点，若某点所施加的荷载大小为F，则各点所施加的各阶模态荷载可表示为式（11）。

[f（i）=F·P·φ（i）·Lk]     （11）

式中：P为1×（k+1）的荷载施加位置矩阵;[φ（i）]为n×（k+1）的各点处各阶的形函数矩阵;n为形函数分析阶数;L为拉索长度。

数值仿真的工况分为无阻尼器工况（UD）、零载电流被动控制工况（Passive-off）、满载电流被动控制工况（Passive-on）和半主动控制工况（SA）四个工况。阻尼器的安装位置为距拉索锚固端6.8 m（4% L）。

3 仿真结果

3.1 一阶强迫振动

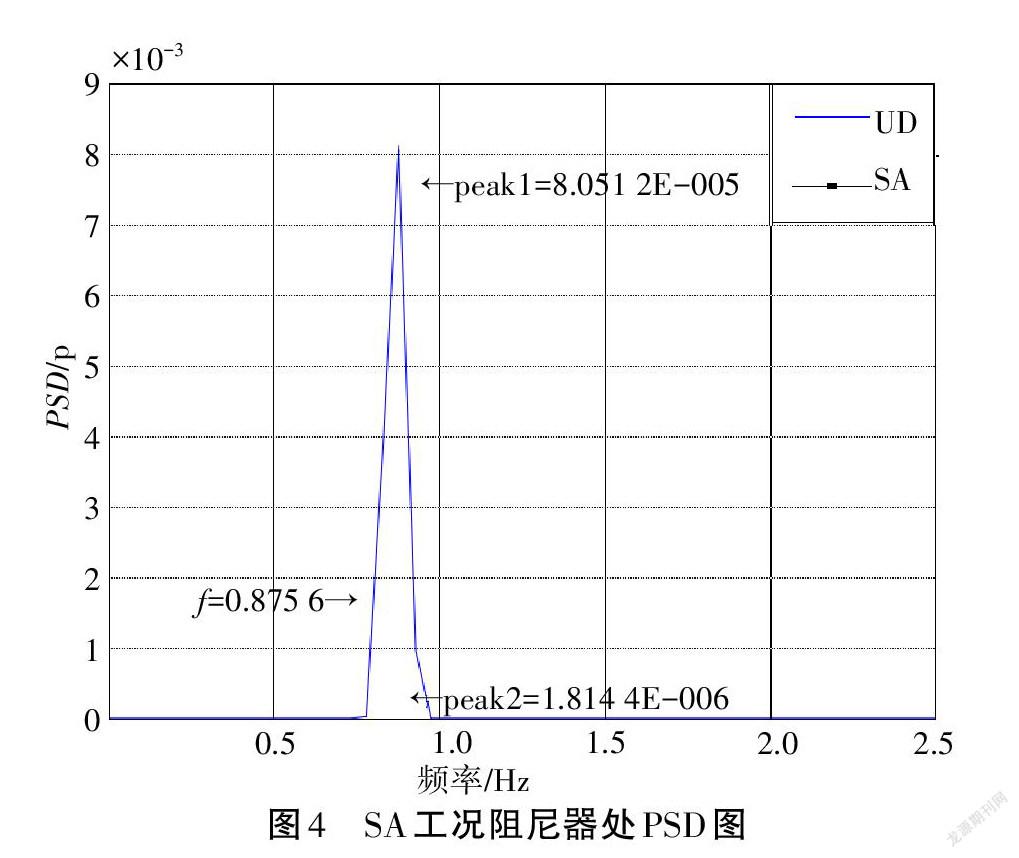
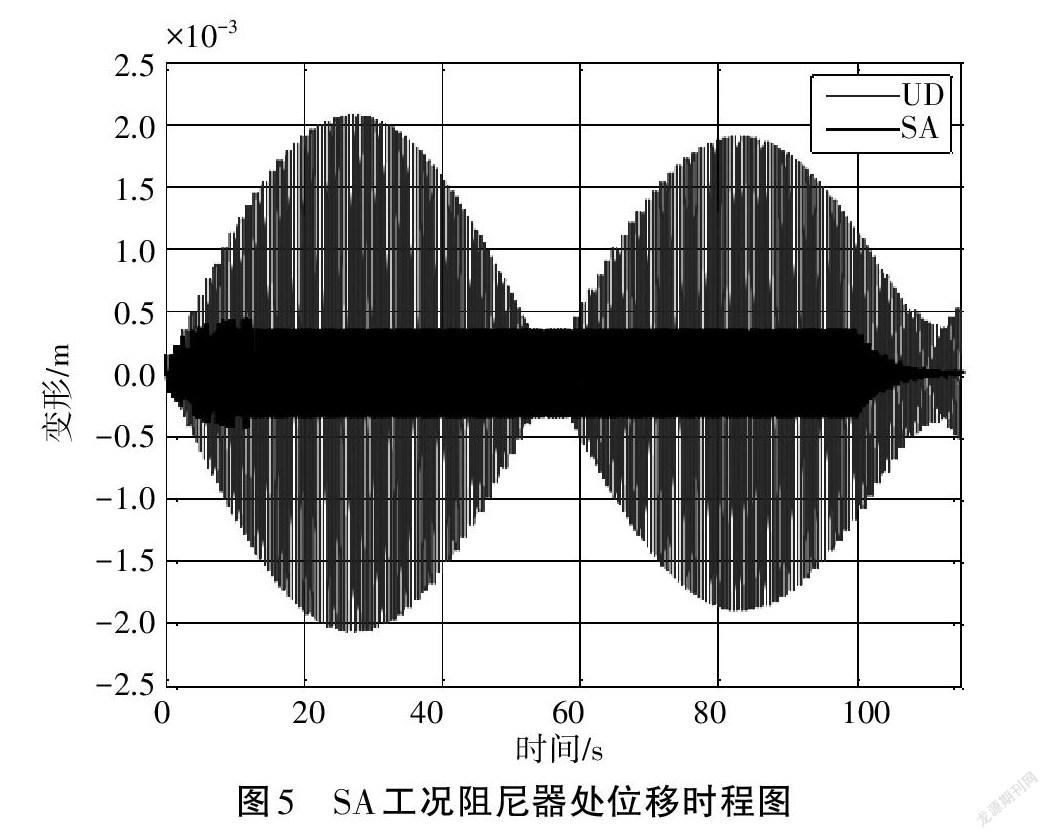
经过仿真分析计算，得到各个工况下各点位在一阶正弦荷载强迫振动下的位移时程图和PSD 图，SA工况下的位移时程图和PSD图见图3、图4。

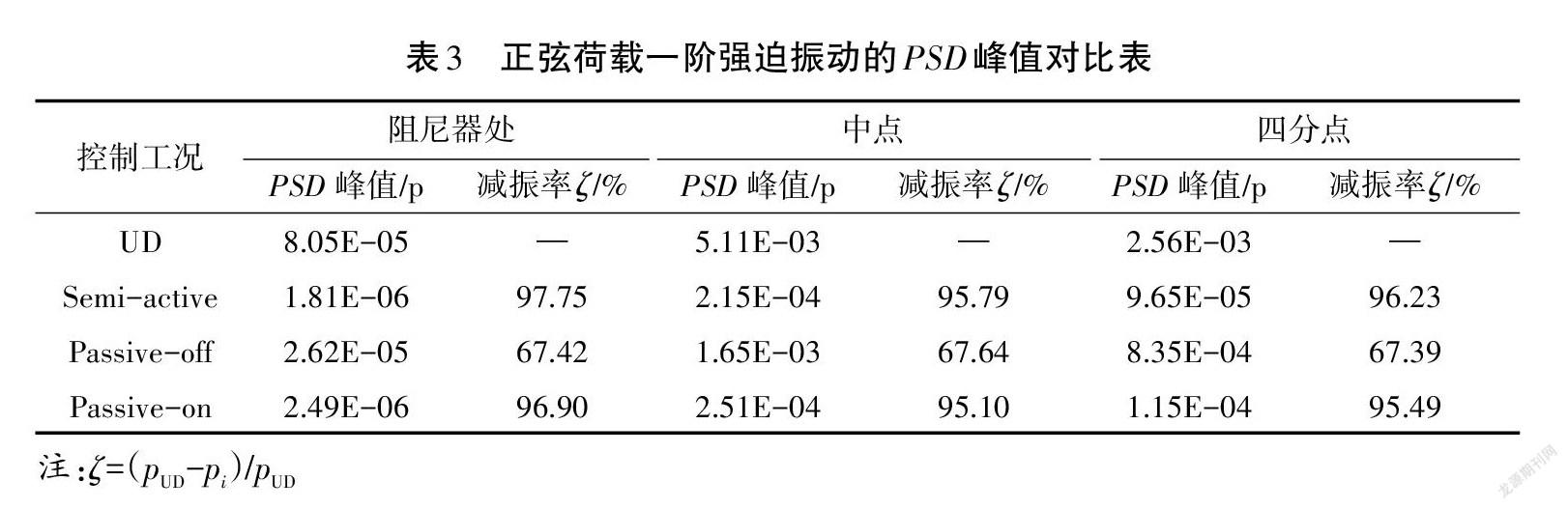
表3列出了拉索-MR阻尼器系统在正弦荷载作用下一阶强迫振动的PSD峰值，从减振率的对比中可以看出，半主动控制的减振效果最明显，说明其对一阶强迫振动能量的削峰作用最佳。

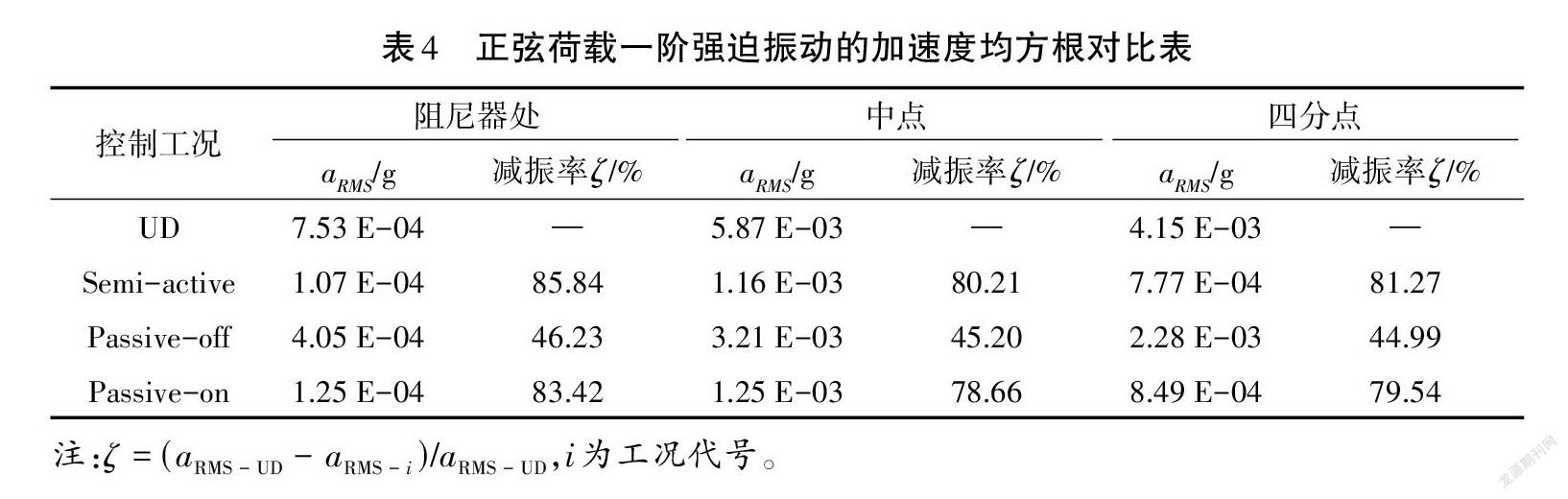
表4为各工况下的加速度对比，从表4中数据可以看出：半主动控制在拉索各点所得到的加速度减振率均为最大值。由此可以看出，半主动控制在拉索强迫振动过程中能较好地控制振动加速度。

3.2 二阶强迫振动

经过仿真分析计算，得到各个工况下各点位在二阶正弦荷载强迫振动下的位移时程图和PSD图，图5和图6为SA工况下的位移时程图和PSD 图。

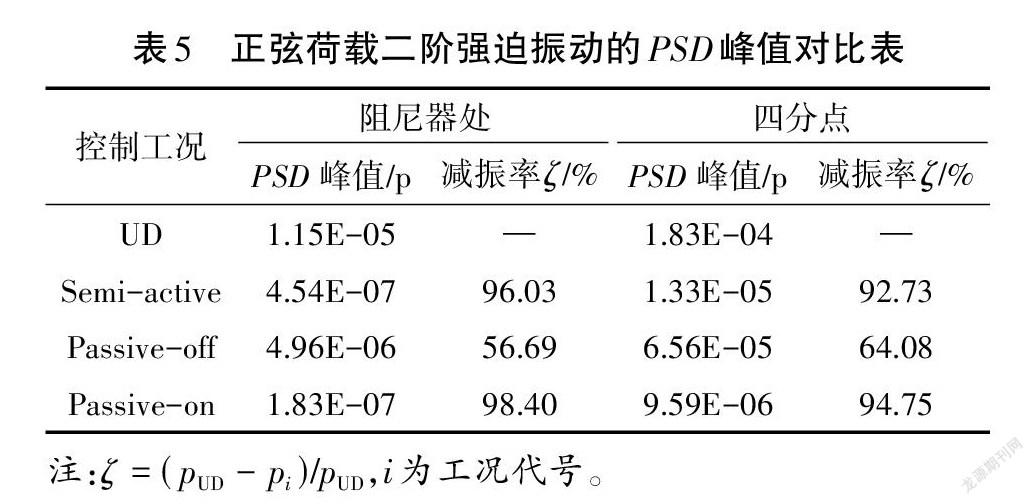
表5为正弦荷载激励下拉索-MR阻尼器系统做二阶强迫振动时的PSD峰值对比表。由于是二阶振动，表中仅列出了阻尼器处和四分点处两点的PSD值。由表中数据可得半主动控制与Passive-on控制的能量减振率基本相当，且远大于Passive-off控制。从减振幅度的角度看，满载电流被动控制的能量削峰幅度在三者中最大。

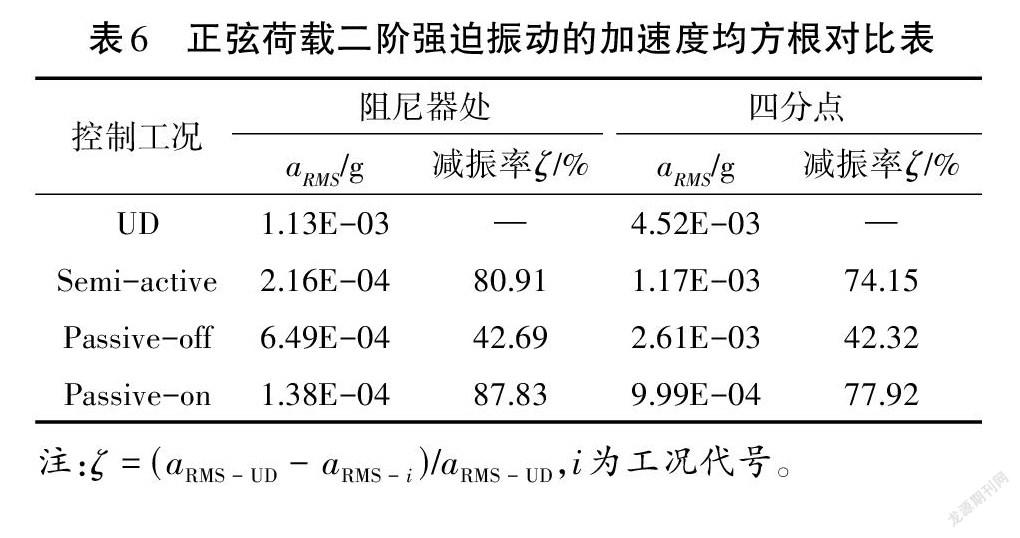
表6列出了三种控制方法对二阶强迫振动的加速度控制效果。半主动控制算法对加速度的控制能力在阻尼器位置处达到最优，与Passive-on 控制相比，加速度减振率略微逊色。

4 结语

本研究以某购物中心拉索为原型，构建了拉索-MR阻尼器系统，提出了半主动控制算法。通过拉索-MR阻尼器系统在正弦荷载作用下的一阶和二阶强迫振动，检验了本研究所采用的半主动控制算法的减振效果。结果表明：基于MR阻尼器双线性力学关系的半主动控制算法能有效减小拉索在强迫振动下的位移，削弱各阶振动的能量峰值，减小各点振动加速度的均方根值，对拉索振动具有较好的控制效果。

参考文献：

[1] DYKE S J， SPENCER JR B F， SAIN M K，et al. An Experimental Study of MR Dampers for Seismic Protection. Smart Structures and Materials[J]. Special Issue on Application to Large Civil Infrastructures， 1999（5）：693-703.

[2] LIU M， LI H， LI J H， et al.，Experimental Investigation on Vibration Control of One Stay Cable Using One Magneto-rheological Fluid Damper[J]. Smart Structures and Materials，2016.

[3] PACHECO B， FUJINO Y，  SULEKH A. Estimation Curve for Modal Damping in Stay Cable with Viscous Damper[J]. Journal of Structural Engineering，1993（6）：1961-1979.

[4] KRENK S. Vibration of a Taut Cable with an External Damper[J].Journal of Applies Mechanics， ASME， 2000， 67：772-776.

[5] 蒋小路.斜拉索减振MR阻尼器优化设计[D].上海：同济大学，2010.