井下微型行星齿轮减速器的设计优化
张 勇,张永勇,陶爱华,杨曙东
(1.中海油田服务股份有限公司油田技术研究院 河北 三河 065201 2.华中科技大学机械科学与工程学院 湖北 武汉 430074)
0 引 言
电动切割工具是一款管内金属锯切井下工具,仪器内部有一个2Z-X(A)(即NGW)微型行星齿轮减速器,将直流电机输出的扭矩放大,并使切割头周向旋转。由于井下条件恶劣,为了保证切割工具有较高的运行可靠性和较长的寿命,设计中要求减速器承载能力好、体积小、高温稳定性好,外壳耐腐蚀[1]。
然而,行星传动设计是一个比较复杂的问题,其体积和重量或其承载能力主要取决于传动参数的选择[2]。按照常规设计方法,当给定传动比、输出轴转矩后,为了求得各轮齿数、模数、齿宽、行星轮数,常常需要先选定其中几个参数,才能求出其它参数。因此,在选择参数方案时,往往没有明确的评估指标,只能选择一个满足设计要求的可行参数方案,后面进行优化设计[3]。下面首先根据常规机械设计经验确定一种可行方案,再基于MATLAB进行优化。
1 行星减速器初始参数设计
井下切割工具仪器直径54 mm,能切割最小油管外径73 mm、厚度5.5 mm。齿轮箱的外径设计同仪器直径,为54 mm,而齿轮箱的外壳最小直径处为螺纹退刀槽,直径为47.4 mm,因此要求齿圈的齿根圆直径小于45.4mm,并且要求所有中心轮中间可以穿过一根直径10 mm的传动杆,因此中心轮齿根圆直径大于12.5 mm,设计要求传动比约120,额定输出转矩21 N·m。经计算,采用4级相同的行星传动,每级传动比约3.31。初始设计参数见表1。

表1 初始设计参数表
根据机械设计手册[4],单级传动比为3.31,选取行星轮个数为np=3,选择中心轮齿数za=38,内齿圈齿数zb=88。验算安装条件、同心条件、传动比条件、邻接条件均满足[5]。再通过第四级的输入扭矩计算齿面接触强度,得出中心轮的分度圆直径,进而选择模数为m=0.5。
因为两齿轮副的中心距相等,且两齿轮齿数均超过最小齿数,不会产生根切,齿轮不需变位,选取标准齿轮。行星齿轮副基本结构参数见表2。
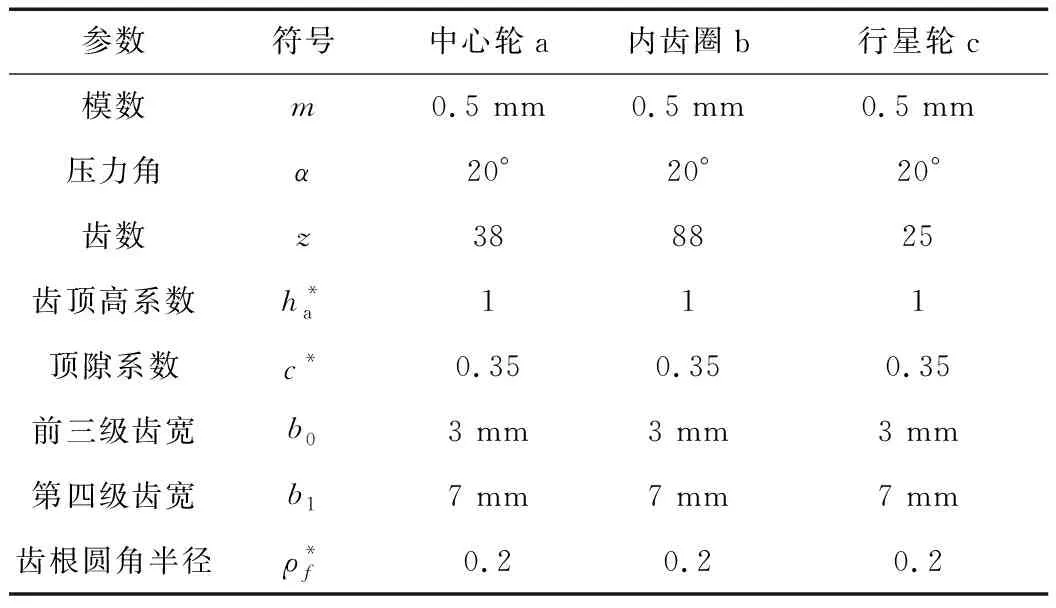
表2 行星齿轮副基本结构参数
此行星轮结构及齿轮副尺寸满足设计要求,经过力学分析及对第三级和第四级的齿面接触疲劳强度校核、齿根弯曲疲劳强度校核,均满足设计强度要求,因此上述方案满足使用要求。
齿圈材料选择井下常用材料17-4PH不锈钢,固溶处理后硬度达到HRC=36,中心轮、行星轮的材料选择18CrMnTi,渗碳淬火处理, HRC=58~62, 接触疲劳极限应力σHlim=1 500 MPa, 弯曲疲劳极限应力σFlim=1 000 MPa,齿轮的精度等级为6级[6]。
2 基于MATLAB优化设计
以上方案显然不大可能是最优方案。为了使设计方案的某种指标达到最佳, 需采用优化设计方法。MATLAB有专门的优化工具箱, 可以快速有效地求解连续优化问题,求解非线性整数规划或混合规划问题,一种常用的方法是分枝定界法,荷兰Groningen大学的KoertKuipers应用分枝定界法编写了现成函数BNB20函数, 可以用来求解带有非线性约束的整数规划或混合规划问题[7]。采用BNB20函数对行星齿轮减速器进行优化设计。MATLAB中BNB20函数非线性规划的数学模型及调用格式为:
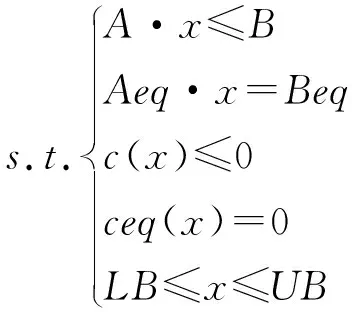
求:minf(x)
调用格式:[errmsg,f,x]=BNB20(f(x),X0,intlist,LB,UB,A,B,Aeq,Beq,nonlcon);
(1)
式中:x是由设计变量组成的向量,f(x)为标量目标函数,X0为设计变量向量x的初始值,intlist矩阵定义整型变量列,对应变量是整型为1,否则为0。矩阵A、矩阵Aeq、向量B和向量Beq定义了线性约束条件,向量函数c(x)和ceq(x)定义了非线性约束条件,向量LB和UB定义了设计变量的下限和上限,nonlcon用于计算非线性不等式约束和非线性等式约束[8]。
2.1 设计变量的确定
行星齿轮传动优化设计中的设计变量一般取模数m、齿数z、齿宽b以及行星轮个数np等。在行星减速器中有太阳轮a、内齿圈b、行星轮c三种齿数,由于行星齿轮传动的机构约束, 其中齿数有两个是独立的,取太阳轮a的齿数za和内齿圈齿数zb为变量。
由校核验算结果可知,第四级行星齿轮传动承受最大的扭矩与应力,设计中比前三级增强了齿宽,如果第四级满足强度条件,那么前三级必然满足条件,受齿宽影响微弱,因此设计中以第四级的齿宽b1为变量。因此确定设计变量为:
x=[za,zb,b1,m,np]T=[x1,x2,x3,x4,x5]T
(2)
式中:za,zb,np为整数;b1,m为保留一位有效数字的小数。
2.2 目标函数的建立
在行星齿轮减速器中, 太阳轮和全部行星轮的体积之和能影响和决定齿圈或整个机构的尺寸和体积,因此选择太阳轮a与行星轮c体积之和为优化目标函数, 目标函数表达式为[9]:
(3)
式中:d1、d2分别为太阳轮与行星轮的分度圆直径。由同心条件2zc=zb-za和d1=mza,d2=mzc得到目标函数[10]:
(4)
代入变量得到目标函数为:
(5)
2.3 约束条件的建立
1)齿面接触强度约束
(6)
式中:Kd为算式系数,直齿传动取Kd=768;KA为使用系数,根据行星齿轮传动设计要求[4],原动机平稳,工作机严重冲击,选择1.75;KHε为综合系数,取 2.4;KHp为计算接触强度的行星轮间载荷分布不均匀系数,取 1.05;φd为小齿轮的宽度系数,φd=b1/mzc;σHlim为齿轮的接触疲劳极限,N/mm2,根据行星齿轮传动设计要求[4],取σHlim=1 500 N/mm2。
(7)
式中:T3为齿轮副中小齿轮的额定转矩,N·m;η为每级齿轮传动效率,0.96。
(8)
令:
(9)
则强度公式(6)简化为:
(10)
代入变量得到齿面接触强度约束条件:
(11)
2)齿根弯曲强度约束
小齿轮c根部弯曲强度最弱, 因此, 取轮c的弯曲强度来建立约束条件。根据对直齿圆柱齿轮轮齿弯曲强度的要求, 得:
(12)
式中:KFβ为计算弯曲强度的齿向分布系数,取1.04;KFp为计算弯曲强度的行星轮间载荷分配不均匀系数,取1.075;YF为齿形系数,近似取YF=4.69-0.63lnza;σFlim为弯曲疲劳极限,σFlim=1 000 MPa。
令:
(13)
则强度公式(12)简化为:
(14)
代入变量得到齿根弯曲强度约束条件:
(15)
3)微型传动、齿宽模数一般关系、齿轮不根切条件
0≤m≤1⟹0≤x4≤1
(16)
3≤np≤4⟹3≤x5≤4
(17)
(18)
4)传动比条件

(19)
(20)
5)安装条件
(21)
6)邻接条件
(22)
(23)
7)两个直径约束
(24)
(25)
2.4 优化设计过程及优化结果分析
首先直接用BNB函数进行第一次优化,将intlist矩阵定义为[1;1;0;0;1],即将齿宽和模数当作连续变量进行优化,之后再进行圆整计算。第一次优化,经过215.5 s,得到优化结果为[44,100,5.4253,0.408,4]。因为齿宽和模数均为保留一位的小数,因此经过圆整计算后得到[44,100,5.7,0.4,4],体积为3 632.988 mm3,而原体积为4 561.789 mm3,体积减少了20.4%。
第一次优化的求解思路是先将所要解决的问题视为一般非线性整数连续优化设计问题来处理。当求得最优解后, 就利用某种策略或技巧来进行圆整处理。由于该权宜之法未充分考虑到问题本身的特点, 可靠性差, 且在整个优化迭代过程中无法提供一系列符合离散要求的迭代点供设计人员选择, 故有必要再辟蹊径解决问题。
由于齿宽与模数均为保留一位数字的小数,因此在第一次优化的程序上稍加改动,将10B1,10 m作为设计变量,将intlist矩阵定义为[1;1;1;1;1],这样就将问题转化为非线性整数优化设计问题。
通过将10B1,10 m带入计算,得到了另一组有效解,且不用圆整,自动就能满足所有条件与要求,[33,75,6.5,0.5,4]得到的体积为3641.204 mm3,体积同样减少了20.18%,但是这组优化解模数相比原来没变化,且齿宽也能够符合机械设计一般要求,更加合理。优化结果与原方案参数对比见表3。
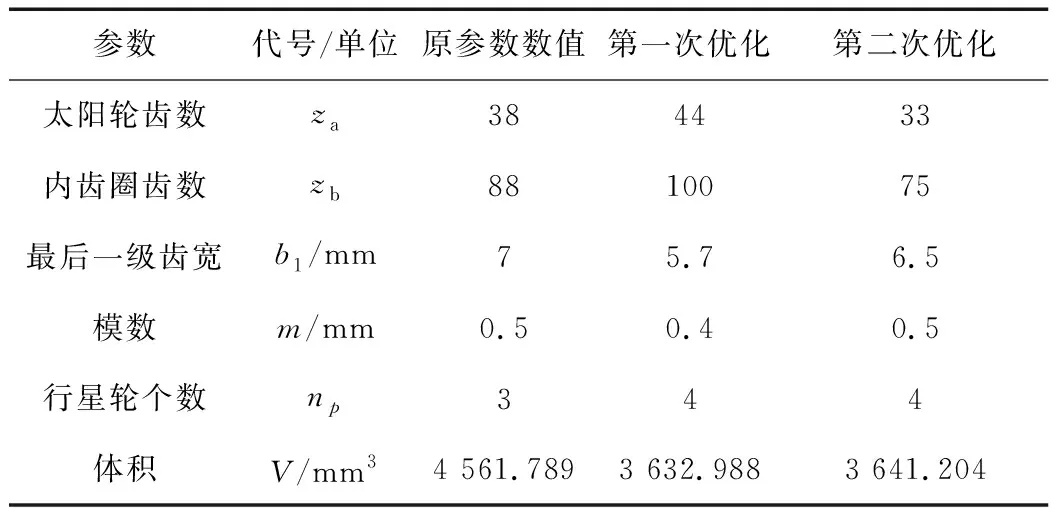
表3 优化结果与原方案参数对比
根据优化后的减速机参数加工样机,如图1所示。

图1 优化后实际加工样机
经过实际应用测试,该行星减速器具有较好的性能,能够稳定运行并提供输出扭矩,无因轮齿失效而造成的损坏,证明了此设计过程的正确性和可靠性。
3 结束语
通过对原行星齿轮减速器进行优化设计,减速器体积比原设计显著减少。通常行星减速器设计方法只能找出可行方案,而以最小体积为目标对行星齿轮减速器进行最优化设计,不仅对缩小减速器体积,而且对减小质量、节约材料、提高承载能力及降低成本等都具有实效意义。
本文中行星齿轮减速器的设计及优化过程对其它同类产品的设计开发具有借鉴作用,基于MATLAB优化设计大大缩短了设计周期,为优化设计提供了一种便捷、可行的方式及思路。当然,体积最小并不是机械产品最理想的唯一优化目标,还有很多其他指标来衡量机械产品的优劣,所以还需要进一步的研究。

