浙江省林业经济增长问题研究
陈周光,崔伟伟,龙飞
(浙江农林大学经济管理学院,浙江 杭州 311300)
林业既是一个重要的物质生产部门,又是一项社会公益事业,是国民经济的重要组成部分以及国家的基础性产业,不但具有经济效益,而且具有较高的生态效益和社会效益,同时在促进农村经济发展、改善农民生活水平方面作用更为突出[1-4].此外,在生态扶贫方面也有显著的成绩,2018 年就有4 个定点扶贫县6.84 万人减贫,贫困村出列数达到了69 个.因此,林业对于社会、经济和生态建设的全面发展具有重要的积极意义[5].据《2018 年全国林业和草原发展统计公报》显示,2018 年中国林业总产值已经达到7.63 万亿元,比2017 年增长7.02%,高于同时期国民生产总值6.60%的增速,表明当前中国的林业经济增长势头较为迅猛.虽然中国的林业经济增长效果显著,但是随着其规模的不断扩大,资源不足、效率不高、经营粗放和机制不顺等问题也逐渐暴露出来[5].林业经济增长作为林业经济发展的前提和基础[6],在很大程度上会影响到中国的林业经济发展.因此,如何促使林业经济持续健康增长已经成为当前亟需解决的问题之一.
经济增长理论认为,经济增长是多种驱动力综合作用的动态过程[4].柯水法等[7]认为经济增长受到生产要素生产率与投入量的影响,在西方经济学中,劳动、资本、土地、企业家才是重要的生产要素.林业作为一个复杂的经济系统,多种生产要素在不同程度上影响着林业经济的增长,如资本、劳动力、林地面积.随着林业经济的不断增长与发展,政策、科技、市场化、产业结构与产业集聚等因素也在不同程度上起着促进作用,丰富了林业经济增长.Chipota 等[8]认为林业投入的增加对林业产业起促进作用.李研等[9]在对中国2005—2016 年的林业数据分析基础上,研究认为以2013 年为分界点,此年之前资本的贡献率大,此年之后则是技术进步贡献率大,而林业劳动力对林业产出没有贡献;柯水发等[7]以中国1978—2011 年的林业产业发展的相关数据为基础,研究认为资本投入是中国林业经济增长的主要因素,产权制度变迁因素也有着正向的推动作用,而刘鹏等[10]以中国31 省市区的面板数据为样本,研究发现林业投资对经济增长具有一定的推动作用,二者之间存在“倒U 型”的非线性关系.张自强[11]认为技术进步是发展现代林业产业的前提.高岚等[12]通过分析广东省林业发展状况,发现资本投入的贡献率为39.5%,造林面积为11.93%,而技术进步则为30.31%,其余为林业产权管制.也有一些学者认为人力资本对林业经济的增长贡献较大[1,3,13].也有学者认为市场化测度是推动中国林业经济增长的重要动力之一[14].近年来,林业生产的空间限制被不断克服,林业产业呈现出一定的空间集聚现象,因此将其纳入林业经济因素研究已经成为新趋向[6].有学者研究认为林业产业集聚对经济增长或者林业经济增长具有促进作用[6,15],而岳喜优[16]发现湖南省林业产业集聚对经济增长起负向影响.夏永红等[17]实证分析了中国林产工业两位数产业集聚及其经济增长的关系,研究发现木材加工业集聚水平具有正向推动作用,而家具制造业和造纸与纸制品制造业集聚水平起着负向作用.魏肖杰等[18]认为林业产业集聚对林业产业健康快速发展有促进作用.廖红伟等[19]以东北地区87 家森工企业为例,研究发现产业集聚对经济增长具有传导效应.
目前对于研究林业经济增长影响因素的方法较多.有学者采用数据包络分析,研究了影响内蒙古林区经济增长的因素,研究结果发现资本与劳动力并未发挥出最大潜力[20].也有学者采用主成分分析法研究了广东省林业产权、要素投入与林业经济增长的关系[12].Qiao等[21]基于C-D 生产函数以及丹尼森经济增长因素理论,对中国1978—2016 年的相关数据研究了市场化进程对林业经济增长的影响.张自强[11]则运用多要素二级CES 生产函数对中国27 个省份的技术进步与林业经济增长进行了研究.柯水发等[7]运用灰色关联度模型研究了中国林业经济增长的影响因素.通过搜集相关文献可以看出,学者利用不同的研究方法,分别探讨了各种驱动要素对林业经济增长所起的作用,为相关研究奠定了坚实的理论与实践基础,但是还存在一些不足,一是关于浙江省林业经济增长问题的研究相对不足;二是将林业产业集聚水平与传统的林业投入要素结合的研究相对较少;三是研究方法较为单一.2017 年国家在《林业发展“十三五”规划》中特地提出了林业产业集聚的作用, 本文将结合灰色关联度模型与柯布- 道格拉斯生产函数, 选取浙江省1990—2018 年的林业产业集聚水平与其他林业生产的相关数据进行实证研究,首先运用灰色关联度模型对影响浙江省林业经济增长的因素进行排序,其次利用回归分析计算出各个影响因素的弹性及贡献度.
1 研究区域概况
浙江省处于中国东南沿海地区,地理位置优越,森林资源丰富,有着“七山两水一分田”之称.根据《2020 年浙江省森林资源及其生态功能价值公告》数据显示,浙江省林地面积为659.35 万hm2,森林面积607.88 万hm2,森林覆盖率在2019 年底达到了61.15%,较为丰富的林业资源为林业经济增长提供了良好的基础.1990 年浙江省林业总产值为5 亿元,而到2019 年其林业总产值则已经达到6646 亿元,30 年间几何平均增长率达到了28.15%,增长速度较快.2019 年林业总产值在国家林业总产值中的占比为8%,其在浙江省国内生产总值中的比重更是达到了10.65%,为国家林业经济增长以及浙江省经济发展做出了较大的贡献.浙江省作为“绿水青山就是金山银山”理念的发端地,林业经济健康持续发展对全国其他地区具有重要的引导作用,因此研究林业产业经济增长具有较强的现实意义.
2 数据、变量与研究方法
2.1 数据来源
为了确保研究数据的一致性与准确性,文中所用数据均来自《中国林业统计年鉴》(1998—2017)、《中国林业和草原统计年鉴》(2018)、《中国林业年鉴》(1990—1997)以及《中国统计年鉴》(1991—2019),文中涉及到林业产值指数和固定资产投资指数来源于《中国统计年鉴》(1991—2019).鉴于数据的可获得性与完整性,本文选择1990—2018 年为研究时间段.
2.2 变量选取
林业经济增长的影响因素众多,一方面资本与劳动力的投入是促进林业发展的两种主要因素[22],另一方面林业产业集聚的重要性也日益凸显,由于林地面积的变化相对较小,所以不予考虑,故选择资本、林业劳动力以及林业产业集聚水平作为投入指标.林业总产值作为林业产出的替代变量,虽然具有一定的不足之处,但是相对于其他数据而言具有代表性并且易于搜集,故选取其为产出指标.林业总产值从1990—2018 年呈现出快速增长的趋势,年均增长率达到了27.97%,尤其是2011 年以后增长更为明显,具体的林业总产值变化如图1 所示.
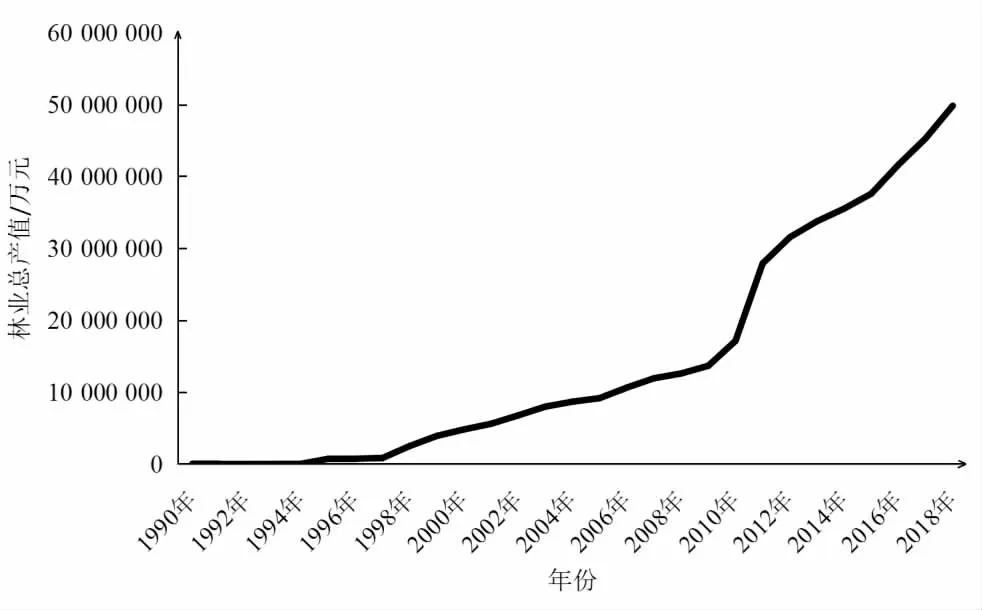
图1 1990—2018 年浙江省林业总产值变化Fig.1 Change of total forestry output value in Zhejiang Province from 1990 to 2018
林业资本.在生产函数中资本是存量的概念,而非流量.因此,从统计年鉴中不能够直接获得,有部分学者直接利用固定资产投资来代替资本存量[9],具有一定的片面性.为了更好的测算,较多的学者采用永续盘存法(PIM).资本存量有广义资本存量与狭义资本存量之分,在本文中仅指狭义的物质资本存量,PIM的具体计算公式如下

式(1)中:Kt和Kt-1分别表示当期和上期的资本存量,It为当期的投资额,δ 为经济折旧率.由资本存量的估算公式可以看出,要准确地计算资本存量必须选取较为准确的投资流量、经济折旧率和投资价格指数.因此,结合本文实际研究需要经济折旧率选取10.96%[23],当年的投资额则选取林业固定资产投资完成额,投资价格指数选取固定资产价格指数对林业固定资产投资进行平减,而基期的资本存量则采用几何平均增长率法计算,计算公式为

式(2)中:g 代表1990—2018 年的投资增长率,投资增长率采用几何平均法求出,其中以1990年基期的可比价格计算资本存量所用的固定资产投资数据.浙江省的林业资本存量从1990 年至2018 年总体上呈现增长趋势,年均增长率为8.49%,但是在2013 年后呈现减少趋势,具体情况如图2 所示.
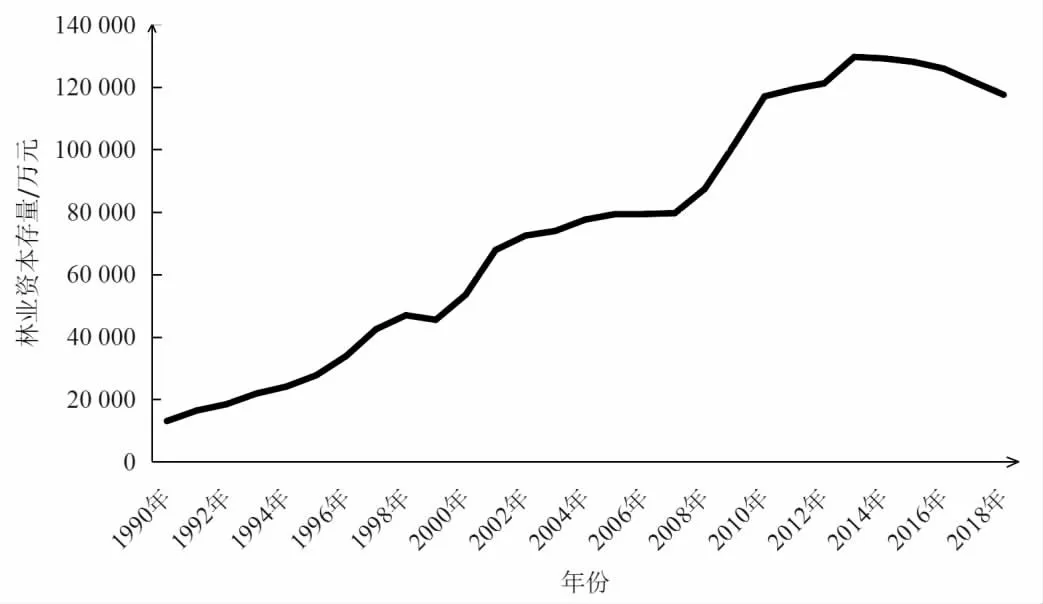
图2 1990—2018 年浙江省林业资本存量变化Fig.2 Changes of forestry capital stock in Zhejiang Province from 1990 to 2018
林业劳动力.由于林业生产的复杂性,林业劳动力的统计较为困难,此文中直接利用统计年鉴中的林业系统年末从业人数替代[9].浙江省1990—2018 年林业劳动力基本呈现逐年下降趋势,特别是从1996年以后趋势更为明显,具体变化如图3 所示.
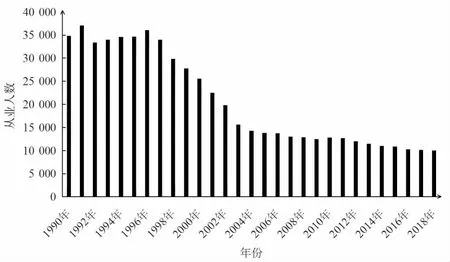
图3 1990—2018 年浙江省林业劳动力变化Fig.3 Changes of Forestry Labor force in Zhejiang Province from 1990 to 2018
林业产业集聚水平.产业集聚可以称为产业地理集中,是某些产业在特定的地域范围内相互集中的现象[24],林业产业集聚则是林业产业相互集中于特定的地域范围内.目前衡量林业产业集聚水平的方法较多,主要可分为产业集中度指数、赫芬达尔指数、区位熵、基尼系数以及产业集聚指数.由于区位熵能够较好地反映出地区专业化程度,并且其侧重地理空间角度,是最为常用的测度指标[25].因此,选择区位熵测度林业产业集聚水平,当区位熵大于1 时,表明该区域林业生产集聚度高;反之,则表明集聚度低.区位熵公式为

式(3)中:wi为第i 年的浙江省林业总产值,Wi为第i 年的全国林业总产值;gi和Gi分别表示的是浙江省与全国第i 年的国内生产总值.浙江省的区位熵1998 年之前略低于1,说明水平较低;而2000 年前后则是突破了2,说明这一时期的林业产业集聚水平较高.从总体来看,浙江省1990—2018 年的区位熵基本位于1 以上,表明林业产业集聚水平较好,具体情况如图4 所示.
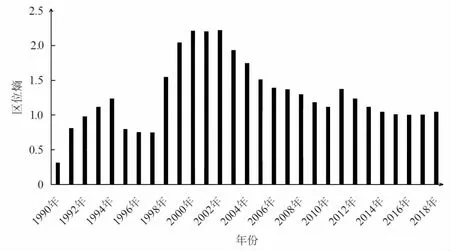
图4 1990—2018 年浙江省区位熵变化Fig.4 Change of location entropy in Zhejiang Province from 1990 to 2018
2.3 研究方法
2.3.1 灰色关联分析法 灰色关联理论是邓聚龙教授于1999 年提出的多因素统计分析方法,主要通过确定参考数列以及比较数列的几何形状的相似程度来判断联系是否紧密[26].关联度指的是两个系统之间的因素随着对象或者时间的关联性的大小的度量[27].若二者间的变化程度相对一致,则表明二者间的相关性强,反之则表明相关性弱.灰色关联分析法计算步骤如下:
第一步,确定母序列和子序列,即参考序列和比较序列.本文将林业总产值作为母序列,林业资本存量、林业劳动力、林业产业集聚水平作为子序列.记母序列为X0(K,子 )序列为X i(K,即 ):X0(K)=.
第二步,数据无量纲化处理.无量纲化处理就是将原始数据量纲不一致的现象加以处理,从而便于得出准确的比较分析结果.无量纲化处理的方法众多,有初值法、均值法等.
第三步,求序列差值、最大值与最小值.
第四步,关联系数计算. 其中分辨系数ρ∈ (0,1),本文取一般值0.5.
2.3.2 生产函数模型 生产函数是估计经济增长最为常用的方法,主要用于分析投入与产出之间的关系,其中以柯布- 道格拉斯生产为主.在估计的参数较多时,常选择超越对数生产函数,然而超越对数生产函数含有变量的交叉项以及平方项,因此容易出现多重共线性问题,故本研究选择更易于估计的C-D 生产函数.
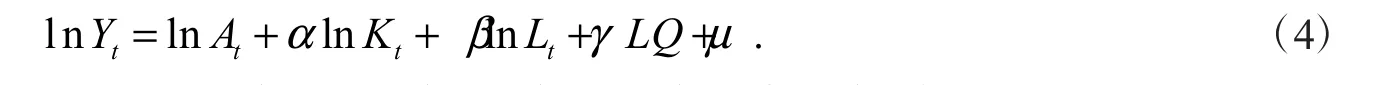

假设C k,C l,Clq分别表示的是林业资本存量、林业劳动力以及林业产业集聚水平的贡献率,贡献率可以有效测度各因素的作用大小,具体公式如下
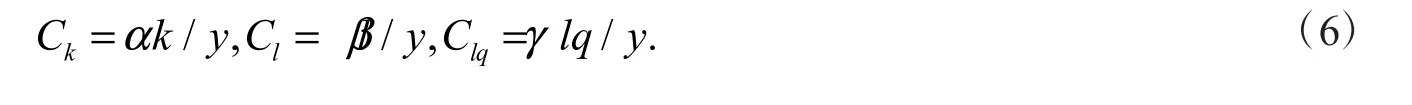
3 实证分析
3.1 浙江省林业产出与林业投入关联度计算
首先将浙江省的林业总产值的时间序列数据作为母序列,然后选择林业资本、林业劳动力与林业产业集聚水平作为子序列,然后根据灰色关联分析的具体步骤进行计算,计算结果如表1 所示.
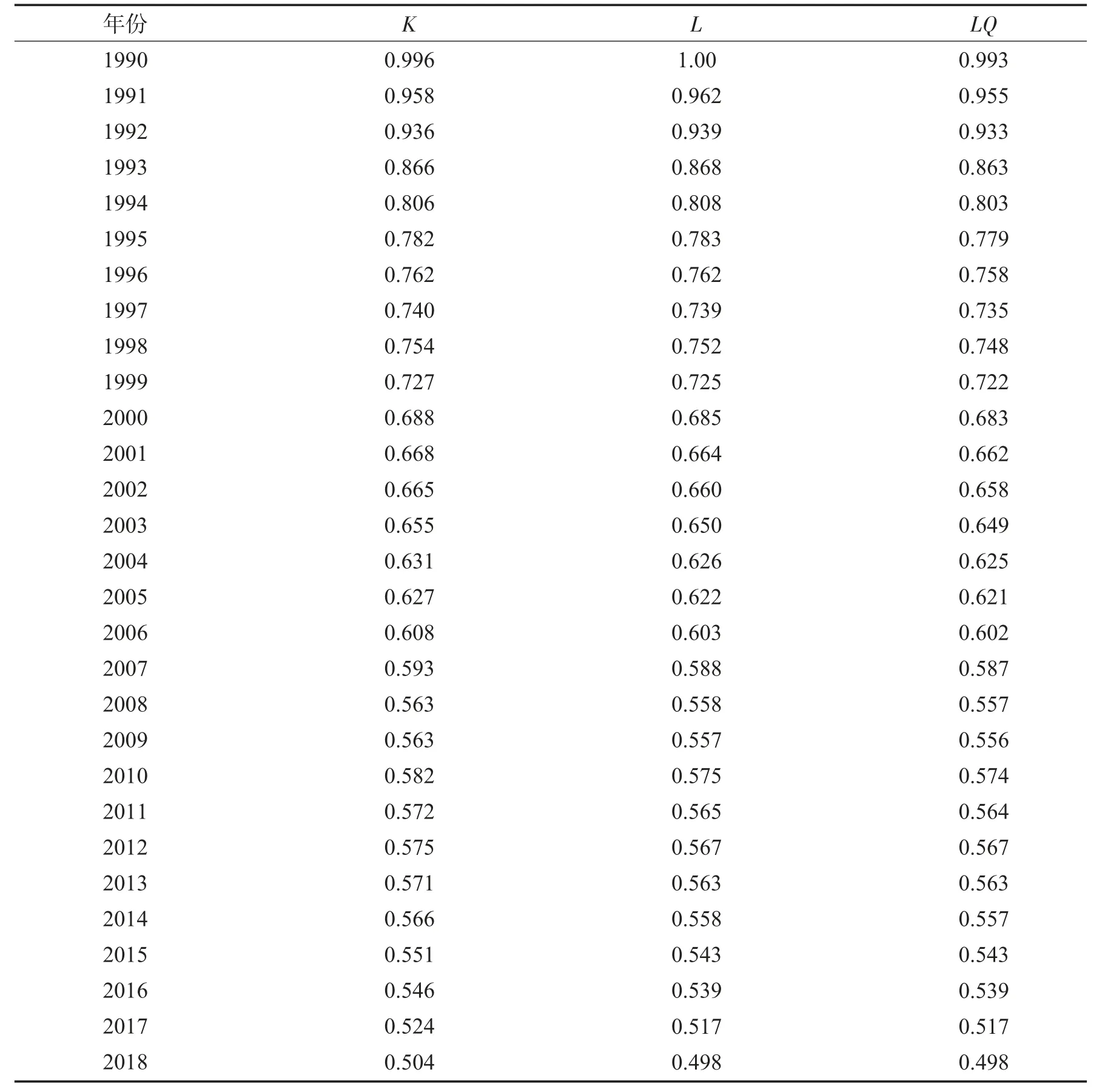
表1 关联系数Tab.1 Correlation coefficient
由上面的关联系数可计算出关联度,计算结果如表2 所示.

表2 浙江省1990—2018 年林业产出与投入关联度Tab.2 Correlation between forestry output and input in Zhejiang Province from 1990 to 2018
由表2可以看出,浙江省林业经济增长与林业资本的关联度最高为0.675;林业劳动力的关联度次之,为0.672;林业产业集聚水平的关联度最低,仅为0.669.本研究的3 个投入要素的关联度均在0.500 以上,这说明在1990 年至2018 年林业资本存量、林业劳动力以及林业产业集聚对浙江省林业经济增长的影响程度较大.
3.2 要素弹性及其贡献率计算与分析
由于本研究是时间序列数据,如果直接采用OLS 回归,可能会出现解释变量与被解释变量之间的高度相关,但是这种相关很有可能是“伪回归”的现象引起的,因此,在回归分析前需要对模型中的各个变量进行单位根检验,以确定时间序列是否平稳.时间序列的单位根检验方法通常是ADF 检验,其原假设是存在单位根,当P 值小于临界值时,拒绝原假设接受备择假设,即不存在单位根.本文利用Eviews10.0 软件进行单位根检验,以判断变量是否存在单位根,检验结果如表3 所示.

表3 变量单位根ADF 检验结果Tab. 3 Variable unit root ADF test results
由表3 结果可知,各变量都小于5%的临界值,可以认为各变量均不存在单位根,故时间序列为平稳序列,因此,可以进行回归分析.
时间序列数据往往会存在序列自相关,存在序列自相关会使得参数估计量的有效性降低,从而影响整个回归结果,采用DW 检验可知,DW 值等于0.6838,由此可知模型存在一阶自相关,同时进一步检验可得模型存在二阶自相关但不存在三阶及以上自相关,因此,需要对自相关进行修正,本研究采用科克伦-奥克特迭代法,检验结果DW 值为1.9094,接近于2,故可以认为模型不存在自相关.
模型中变量之间严重的线性相关关系往往会使回归系数值的意义与经济理论不相符[1],从而导致回归结果不准,检验多重共线性的方法有直观观察法、相关系数矩阵法及方差膨胀因子法等,本研究选择VIF 值(方差膨胀因子)判断,若VIF 值大于10 则存在多重共线性,小于则没有,利用Stata15.0 分析,检验结果如表4 所示.

表4 多重共线性检验结果Tab.4 Multicollinearity test results
由表4可知,各个变量的VIF 值都小于10,故而可认为模型不存在多重共线性问题.由于本研究已经对原始数据进行了对数化处理,缓解了异方差的干扰,并且通过White 检验可知P>0.05,故不存在异方差.回归分析结果如表5 所示.
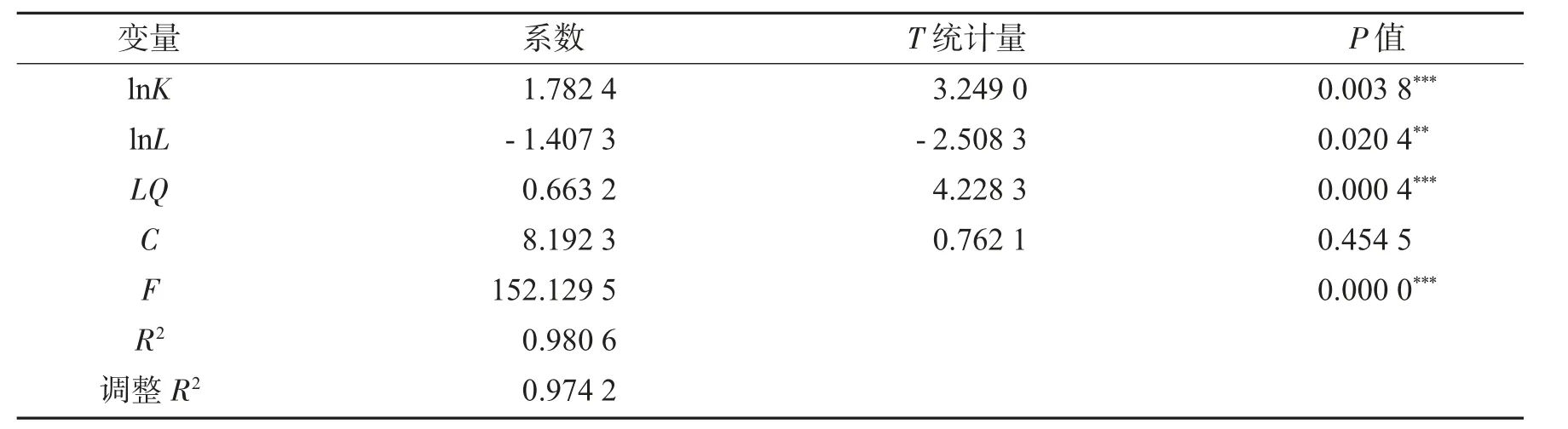
表5 回归分析结果Tab.5 Regression analysis results
根据表5 的估计结果可知,F 值等于152.1295 且P 值小于临界值,说明模型整体上显著,调整R2为0.9742,说明模型的拟合度较高,同时各个变量分别通过了5%以及1%的显著性水平,表明该回归方程中林业资本存量、林业劳动力以及林业产业集聚水平对林业经济增长有重要作用,因此回归方程如下
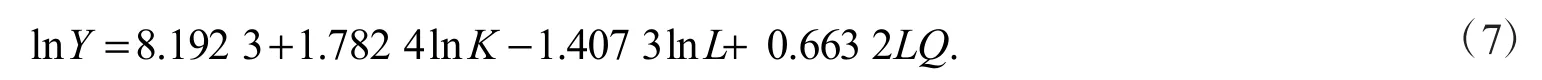
从该回归方程中可以看出,林业劳动力、林业资本存量以及林业产业集聚水平对于林业经济增长存在着较为稳定的线性关系.其中林业资本存量的产出弹性为1.7824,说明林业资本存量每增加1 个单位,林业产出就会增长1.7842 个单位;林业产业集聚水平的产出弹性为0.6632,说明林业集聚水平每增加1 个单位,林业产出就会增长0.6632 个单位;虽然林业劳动力的弹性为负数,但不能认为林业劳动力的投入增加会降低林业产出[9],回归结果表明在一定程度上林业经济增长对资本投入的变化更为敏感.总体来看,林业资本对浙江省1990—2018 年的林业经济增长的拉动作用要高于林业劳动力以及林业产业集聚水平.
结合获取的林业系统年末从业人员数据发现,浙江省1990—2018 年林业系统年末从业人员逐渐减少,而林业总产值却没有受到明显影响,两者在很大程度上呈负相关关系.可能原因是林业生产中机械化程度不断提高,在一定程度上降低了对林业劳动力的依赖,同时随着中国工业化的逐步发展,从事林业的劳动力很可能脱离林业生产从事其他行业,也可能由于林业生产周期较长,这些因素共同导致了二者出现负相关关系.
本研究按照6 个时间段进行,最后计算1990—2018 年总的年均贡献率.根据公式(6)可以计算出浙江省1990—2018 年林业资本存量、林业劳动以及林业产业集聚水平的每个时间段的年均贡献率,计算结果如表6 所示.
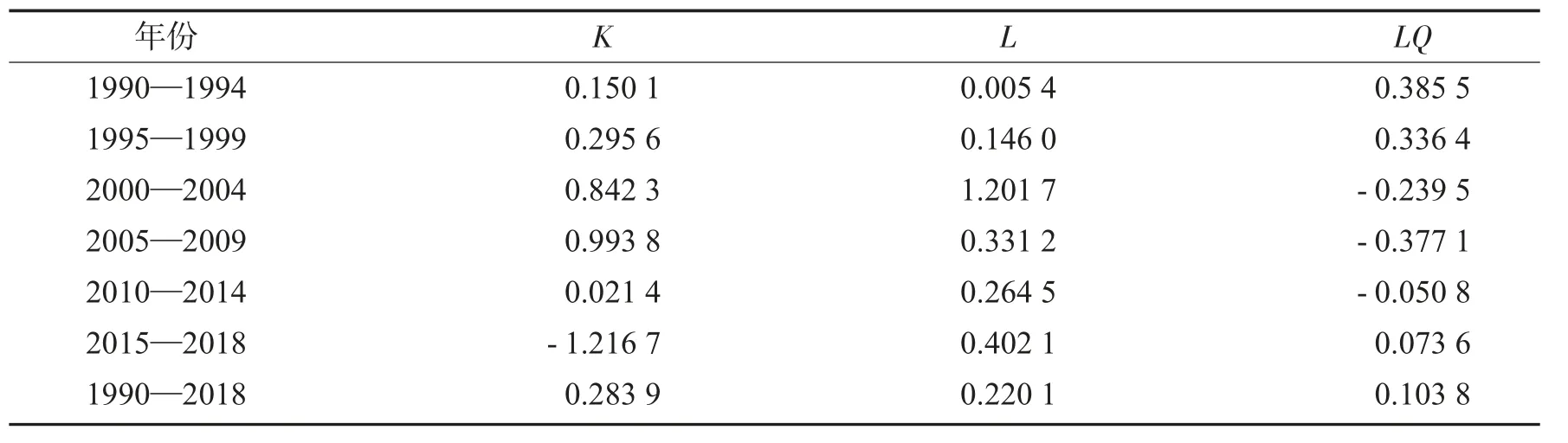
表6 各投入要素对浙江省林业经济增长的年均贡献率Tab.6 The annual contribution rate of each input factor to forestry economic growth in Zhejiang Province
分时间段来看,林业资本存量与林业劳动力基本呈现先增加后降低的趋势,原因可能是在林业经济刚发展时,需要投入巨大的资金与劳动力,因此导致贡献率增加.但是随着中国经济增长进入新常态,林业经济发展模式也随之发生变化,进而使得存量林业资本和林业劳动力、贡献率有所降低,林业产业集聚水平贡献率呈现先降低后增加的趋势.从1990—2018 年的年均贡献率来看,林业资本存量的年均贡献率为28.39%,林业劳动力的年均贡献率为22.01%,林业产业集聚水平的贡献率为10.38%.通过对比可以看出林业资本对于浙江省1990—2018 年林业经济增长的贡献最大、林业劳动力次之、林业产业集聚水平最小.总而言之,林业资本、林业劳动力以及林业产业集聚水平都对浙江省林业经济增长做出了贡献.结合表5 和表6可知,虽然林业劳动力的弹性系数为负,但是年均贡献率为正,验证了上面的结论,即增加林业劳动力投入并不会降低林业总产值.由表6可知,林业产业集聚水平的贡献率最低,可能原因是浙江省的林业产业集聚水平呈波动下降的趋势,因此,导致其平均贡献率较低.总体结果表明浙江省1990—2018 年的林业经济增长主要依赖于林业资本与林业劳动力,但是从动态时间序列来看,林业资本与林业劳动力的贡献率呈现出波动下降的趋势,林业产业集聚水平则为波动上升,说明单纯的依靠林业投资与林业劳动力的投入已经略显不足,应该需要关注林业产业集聚以及其他因素的带动作用.
4 结论与讨论
本研究将林业资本存量、林业劳动力以及林业产业集聚水平纳入林业经济增长模型中,首先运用灰色关联分析法研究了各投入要素对林业经济增长的影响.结果表明,林业资本存量与林业经济增长的关联度最高,为0.679;林业劳动力次之,为0.672;林业产业集聚水平最低,为0.669.其次将林业产业集聚水平作为生产要素引入扩展的C-D 生产函数中,研究各要素对林业经济增长的弹性系数以及贡献率.实证结果表明,林业资本存量的弹性系数为1.7842,说明林业资本存量每增加1 个单位,林业经济就会增加1.7842 个单位;林业产业集聚水平的产出弹性为0.6632,说明林业集聚水平每增加1 个单位,林业经济就会增加0.6632 个单位;而林业劳动力弹性系数为-1.4073.然而从年均贡献率来看,林业资本存量的年均贡献率最高,林业劳动力贡献率大于林业产业集聚贡献率,可以看出林业资本存量的年均贡献率与林业劳动力的年均贡献率差异不大,二者的贡献率并不高,说明林业经济增长不在仅依靠林业资本存量以及林业劳动力的单纯的数量投入,更多的是结构与质量及其他因素.动态变化显示3 种投入中林业产业集聚的贡献率在波动增长,另外2 种则波动降低.在本研究中综合两种方法可以看出,在浙江省1990—2018 年的林业经济增长中林业资本与林业劳动力的作用依然比较大,林业产业集聚作用较小.
浙江省森林资源较为丰富,为林业经济增长提供了前提,1990—2018 年浙江省林业经济增长迅速,为国家整体林业经济增长做出了突出贡献,然而研究中发现,林业资本存量以及林业劳动力的年均贡献度不高.因此,需要重视质量与结构的作用,林业产业集聚的年均贡献度虽然较低,但是具有较大的发展潜力.2021 年5 月11 日,浙江省发展改革委、林业局印发了《浙江省林业发展“十四五”规划的通知》,该通知将会为浙江省林业经济健康可持续增长奠定基础.林业经济是复杂的经济系统,需要统筹规划,在传统的生产要素的投入的基础上,要加快转变林业经济增长方式,注重林业投资的效率与结构、加大林业人才与科技的投入、优化林业产业结构、提高林业产业集聚水平、健全林业产业相关政策.本文仅研究了林业资本存量、林业劳动力以及林业产业集聚这3 种因素对林业经济增长的影响,然而影响林业经济增长的因素众多,今后可纳入更多因素并结合面板数据进行实证研究.

