一种奇特反射光环的物理原理探讨
郑仁蓉,朱顺泉


摘 要:生活中的实验发现:小束、分离的平行太阳光线照在黑暗中直立的金属圆柱形凸面镜上,反射光线会在地面上形成漂亮的光环或光区。这种现象产生的原因来自平行的入射光线以及入射点的法线在水平方向,并呈对称和发散排列。二者导致所有反射光线与竖直方向的夹角相等、等高入射点的反射光线在地面上的投影点与过入射点到地面垂线的距离相等。反射光线相对于自身入射点的法线(即对应圆柱水平圆周半径的延长线),偏离的水平投影从0到最大值π/2。由此导致只照亮水平截面半个圆周的入射光线,经反射后可以得到地面上整个闭合的光环,也使光环偏离准确的圆形。
关键词:几何光学;圆柱形凸面镜反射;半圆周柱形光立柱
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2022)5-0001-5
光的反射是光学中历史悠久的基本概念。平行光线束照射在凸面镜上,反射光线会发散开来[1],这个事实在拐弯镜、汽车后视镜等镜中虚像的应用,更是司空见惯。但是,竖立在黑暗中的金属圆杆,作为一种特殊的凸面镜,当平行光线照射其上时,会发生什么情况呢?这种偶尔一见但常被人忽视的现象,正是本文要讨论的问题。
1 现 象
2021年初,中午时间,室外灿烂的阳光透过窗帘照进海南三亚某正南向的房间。机缘巧合,笔者像往常一样走进房间,突然发现,一把椅子的一条前椅腿影子正好位于从窗帘缝透进来的、长条形太阳光斑的正中间,即太阳光线正好照亮了黑暗中整条前椅腿的向阳面,地面有一个以椅腿着地点为中心的圆形光亮区域,光亮的周边还有一些黑影,引人瞩目,如图1(a)所示。
这一现象引起了笔者的注意,随后将椅子搬到阳台上继续实验。拉上窗帘只留一条小缝,因为窗框的阻隔,透过窗帘缝射进阳台的太阳光线,照在地面上被分隔成一长两短的三个白色明亮的小光斑,将椅腿的着地点置于长光斑的末端,让椅腿影子穿越三个阳光小光斑。被窗帘和窗框分隔成三小段的阳光光束,照亮了椅腿半个圆周柱面的三个不同高度。椅腿位置刚一摆好,地面上就形成了以椅腿着地点为中心的、途经太阳光斑的一个中心小反射光区和两个外围反射光环,如图1(b)所示。
用直立的圆柱形金属杆代替椅腿,进行与图1(b)完全相同的实验,得到图1(c)。二图相比较,反射光环图案的差别仅仅在于图1(c)中金属杆的顶端被一段长条形太阳光束照亮,因而地面上多出一条最外围的、较宽的光环。图1(b)中缺少这条最外围且最宽的光环,这是因为椅面的遮挡,它使图1(b)中光环的清晰度远大于图1(c),却也使椅腿参与反射太阳光线束的有效长度比圆柱形金属杆短。
挪动金属杆的着地点位置,得到图1(d),因为都是长条形太阳光线束照亮整个圆柱形金属杆的半个柱形圆周,图1(d)与图1(a)相似,反射图形都是一个以椅腿着地点为中心的圆形光亮区域,其周边还有一些黑影,只是图1(d)中多出来一个三角形黑影。去掉金属杆圆孔中的长树枝,用手捏住图1(d)中金属杆的顶端,让金属杆绕着自己竖直方向的中心轴转动,会发现地面上的反射光区,包括光区中的各种黑影,也跟着转动。这充分说明,图1(a)和图1(d)中反射光区的黑影来自于反射主体金属杆表面自带的印迹,是这些污迹阻碍了太阳光线的正常反射。
用型号为SDLaser.303的激光笔替代阳光充当光源,以约30°的入射角照射在金属圆柱体上,得到图1(e)。如果激光入射点在金属圆柱体上的位置高度不变,则地面上绿色反射光环的直径会随着入射角的增大而变小。为什么图1(e)中绿色反射光环没有像前面四个反射图形那样形成封闭的圆形图样呢?根据光的直线传播,入射光线只有完全照射圆柱体向光的半个圆周面,才能形成地面上封闭的反射光环或光区。图1(e)中反射光环没有封闭,说明激光笔发射的激光束的宽度小于圆柱体的直径。
2 地面上光环或光区图案的理论解释
2.1 圆柱形金属杆的边界入射点和正入射点的反射光线与地面图案的对应关系
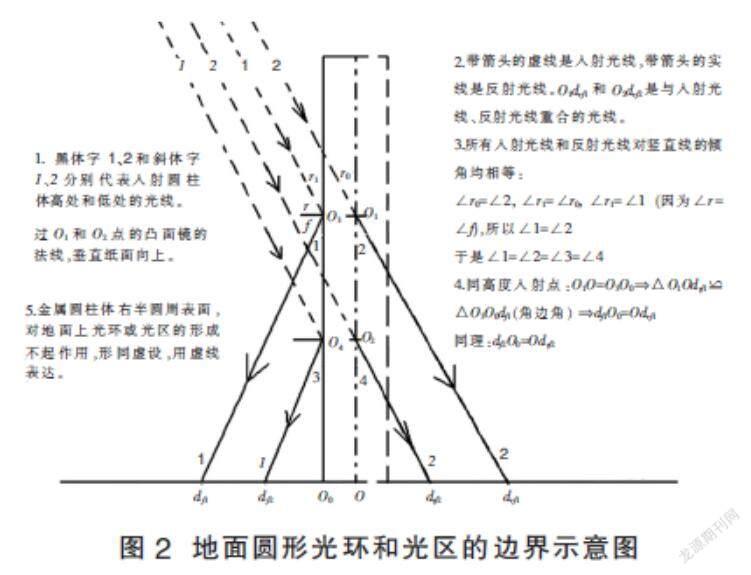
实验中入射的平行的太阳光线因窗帘和窗框的遮挡而被分隔开来,形成小光束。因为光线直线传播,站立在黑暗中的金属杆凸面镜只有向阳的半个圆周能够接收并反射太阳光线,如图2所示。
图2中的点划线表示圆柱形金属表面圆周正中间的竖直线,是照亮半个圆周入射太阳光线束的起始点和切点所在地。与它相对的图2中点划线的正后面,是圆柱上向阳的半个圆周的终点, 它们在图2的正视图上是重合的。
(1)图1(b)中,地面上的光环或光区图案的右边界为什么总是与太阳光斑相重合?
看图2中黑体字2所代表的光线,它入射到圆柱高处一水平截面圆周上的边界入射点O1,过入射点O1的法线,是圆柱同一水平截面圆上过O1点的半径延长线,垂直纸面向上,边界入射光线和边界反射光线2的入射角和反射角(图2中无法显示):
入射角∠r2=π/2(1)
反射角∠f2=π/2(2)
二者相加:∠f2+∠r2=π (3)
以上说明:从边界入射点O1起始的反射光线会与明亮的入射光线重合,一起直达落地点drf1,所以格外明亮。再加上有宽于圆柱体直径的直射地面的太阳光线,一起形成了图1(b)中小光环右侧边界与太阳光斑相融合的明显特征。图1(c)与图1(b)完全相似,读者可以自己看看。
照亮圆柱水平截面半个圆周的边界入射光线,竟然直达地面光环的右边界,说明对地面上光环图案起作用的只是圆柱体中向阳的半个圆周柱面。背光的半个圆周柱面不起作用,形同虚设。
图2中的正入射光线1,经过与边界入射点O1在同一水平截面的正入射点O3反射后,成为正反射光线1,其落地点在df1。因为df1仅仅是“反射”光线的落地点,亮度本应大大小于drf1,但在實验照片图1(b)(c)中,df1在入射光线明亮的投影之中。正入射点O3的特点是:它是圆柱确定的水平截面半圆周弧度正中间的唯一一个阳光“正”入射的点。97F55C8E-96FE-4889-ABCE-291E981564C3
(2)地面上,组成反射光环或光区的亮点是怎么形成的?
由图2及图面中说明3、4可知:对应光线1的正入射点O3,有:
∠f=∠r(反射角=入射角),又∠r0 =∠2(对顶角相等) (4)
∠r1=∠r0(两边分别平行的两个角相等)
∠1=∠r1(直角减去相等角的差相等)→
∠1=∠2 →Δdf1O0O3≌drf1OO1(角边角)(5)
→df1O0=Odrf1(全等三角形对应边相等)(6)
(6)式说明图2中入射光线1、2经凸面镜反射后的落地点df1和drf1在同一个光环上。圆柱体过O1和O3竖直母线的着地点O和O0的位置相差1/4圆周,所以落地亮点df1和drf1不在同一条直径上,二者会相差圆柱体影子的一个半径宽度。
再看图2中,斜体字所代表的正入射光线1和边界入射光线2,它们是图1(b)中椅腿着地点向上的小束平行入射光线的上部边界光线,它们在圆柱面低处、同一水平截面半圆周上也有两个相隔1/4圆周的正入射点O4和边界入射点O2,分别与光线1、2对应的正入射点O3和边界入射点O1在圆柱表面同一条竖直的母线上。因为平行线间同位角相等、直角减去等角后余角相等有
∠1=∠2=∠3=∠4(7)
Δdf2O0O4≌Δdrf2OO2(角边角)(8)
→df2O0=Odrf2(全等三角形對应边相等)(9)
光线1、2经圆柱表面反射后形成图1(b)中地面上以椅腿着地点为中心的小光区中,沿着入射光线方向左右边界的两个亮点df2、drf2,它们在同一个圆周上,但不在同一条直径上。因为同一水平截面正入射点O4、边界入射点O2点的位置低于圆柱高处水平截面相应的O3和O1点,所以对应的df2和drf2点的位置离直线O0O3和OO1的距离更近,即
O0df1>O0df2、Odrf1>Odrf2 (10)
与图1(b)的情况一致。
值得注意的是(7)式中的4个角相等,说明至少在图2探讨的两组光线中,所有反射光线与竖直方向的夹角都相等,都等于入射平行光线与直立圆柱体母线的夹角。正是这个重要的结论,才导致入射到圆柱形凸面镜同一水平截面半圆周上的不同点的反射光线形成的各自的直角三角形全等,见(5)(8)式。于是,反射光线在水平地面上的落脚点形成光环或光区上的亮点,见(6)(9)式。且入射点在立柱上的位置越高,则对应地面上光环或光区的“半径”越大,见(10)式。
但是,反射光线与竖直方向夹角始终相等。这个重要的结论是否对圆柱形凸面镜上任意高度水平截面上、向阳半圆周上、其他任意的入射点都成立呢?
2.2 圆柱形凸面镜向阳的半圆周上、其他任意入射点的情况讨论
图1(b)中地面上一个确定的光环,是由包括圆柱体影子在内的太阳光斑线作为对称轴的、两个对称的“半个”光环合在一起组成的。两个“半”光环之所以对称,是因为形成地面上半个光环所对应的不同的入射点,均分别在圆柱形同一水平截面正入射点和两个边界入射点之间。如果任意入射点的法线(过入射点的半径延长线),与正入射点法线组成的圆柱水平截面圆的圆心角相等,则此两入射点及对应法线相对于正入射点及法线的位置对称。所有同一水平截面半圆周上的入射点和相应的法线位置均相对于正入射点的法线两两对称分布。
入射光线经圆柱同一水平截面1/4圆周上连续排布入射点,反射以后形成同一侧地面上半个光环; 而圆柱同一水平截面相邻的后半个1/4圆周上的入射点,反射后产生地面上后面另外一侧半个光环。而地面上半个光环的形成,根据前面的论述,只需考察反射光线、入射光线与竖直方向的夹角是否相等。因此,现在只需补充同一圆柱水平截面1/4圆周中间任意一个入射点,其反射光线和竖直方向的夹角。如图3所示。
图3中,平行入射光线前进方向始终不变,但因为过圆柱同一水平截面半圆周上、不同入射点的圆柱面的法线,是同一半圆周上不同半径的圆外延长线,法线方向一直在变化,导致光线1、2、3的入射面的方位和入射角的大小也跟着变化。
图3中,光线1的入射点是正入射点a,法线为aa1,入射面与地面的夹角设为∠m1,有∠m1=π/2,即光线1的入射面与地面垂直。光线3的入射点是边界入射点c,法线为cc1,入射面与其他入射光线平行,与水平地面的夹角设为∠m3,∠m3为锐角。
对应任意入射点b的光线2的入射面与地面夹角∠m2为锐角,大小介于光线1和光线3的入射面与地面夹角之间:π/2=∠m1>∠m2>∠m3。
光线2虽与光线1、3的入射方向平行,但因光线1、2、3所对应的同一水平截面圆周上不同入射点的法线,即圆柱水平截面圆周半径的延长线 aa1、 bb1和 cc1的发散性,使对应不同入射点的平行入射光线的入射角大小也在变化。光线2的入射角介于光线1和光线3之间,即∠r1<∠r2<∠r3=π/2。反射定律规定,反射光线和入射光线必须在对应法线的两侧,且反射角=入射角,于是导致反射光线相对于自身的入射光线,比法线间有更强的发散性。比如,正入射点到两个边界入射点的法线相差π/2,于是对于方向不变的入射光线,从正入射角最小,变到边界入射角为π/2。图3的光线3,如同图2的光线2,实现了最大的反射角[见(1)(2)式]∠f3=∠r3=π/2,而边界入射点的边界反射光线3(实线),相对于它自身的边界入射光线3(虚线),就偏离了π(2×■),加上与光线3对称的、正入射点后侧的边界入射光线3',也与对应法线成π/2的入射角,反射光线3'相对自身入射光线也偏离了π(2×■)。因为π+π=2π,于是形成了水平地面上圆柱影子两侧、整个光环合拢的亮点。97F55C8E-96FE-4889-ABCE-291E981564C3
正入射点与边界入射点的反射光线提供了地面上光环的边界亮点,再加上其间连续分布的其他任意入射点上的反射光线在地面投影亮点的补充,就是地面上整个光环的成形。
图4是图3中光线2的放大图,以考察光线2的反射光线和竖直方向的夹角是否与入射光线和竖直方向的夹角相等。如果相等,就说明反射光线2的着地点与光线1、3的着地点都落在地面上同一个反射光环上。
因为光线2的入射点是圆柱体水平截面1/4圆周中任意一点,把光线2的情况说清楚,加上光线1、光线3,就把入射点在圆柱水平截面1/4圆周上的入射点都弄明白。再根据对称性,圆柱上相邻的后面1/4圆周上的入射点反射后给出了地面上另外一半的光环线。
在图4中的入射面G内,作入射光线EO的延长线OC(作为辅助线)。OA是反射光线,截取OC=OA,连接AC,取AC的中点B,连接OB,则OB⊥AC(等腰三角形底边中线即垂线);过B点作竖直的圆柱体表面母线OD的垂线,垂足为D,即BD⊥OD。
根据三垂线定理可知:AC⊥BD→ΔADB≌ΔCDB(边角边)→AD=CD→站立的两个直角三角形全等,即ΔADO≌ΔCDO(边边边)→∠AOD=∠COD
又因為∠EOH=∠COD(对顶角相等)(11)
于是∠AOD=∠EOH,即反射光线OA与圆柱竖直方向的夹角和入射光线与竖直方向的夹角相等。
以上讨论的本质在于圆柱形立柱的竖直方向不变、太阳光线平行入射的方向也没有改变、反射光线受反射定律支配,大小、方向都有规定,因对顶角相等[见(11)和(4)式],而与入射光线和竖直方向的夹角挂上钩。
由此也说明所有照亮圆柱形凸面镜同一水平截面半个圆周的入射光线,确实给出地面上除了圆柱体影子以外的整个“圆周”光环亮线。
图4中,特意将OB延长至OB1、作B1D1⊥OD1、过B1作AC的平行线,分别与OA、OC的延长线相交于A1、C1点,连接A1D1、C1D1,因为OD1>OD,必有D1A1>DA,与图1中,平行太阳光线束照在椅腿的位置越高,对应的地上光环的“半径”越大,是一个道理。因为所有反射光线与竖直方向的夹角相等,必有当反射光线投影的水平面与入射点所在平面的距离越大,反射光线投影点与过入射点的圆柱面竖直母线间的距离越大,所有反射投影点连成的光环的“半径”也越大。
利用图4的图面说明6、顺带证明支配真实光线的反射定律的规则,当真实光线投影到水平面上一样适用。因为圆柱形凸面镜表面的法线本身就是水平方向上的直线,它投影到水平地面上的走向一点也没有改变。而入射光线、法线、反射光线三线又在同一平面之上,反射角等于入射角,投影到水平地面上的定性关系也不会改变。
2.3 形成地面上一个反射光环图像的几何解释
图5可以看成是图1(b)(c)中,地面上一条细光环形成的写照。图中删去圆柱体右侧半个圆周柱面丝毫不影响地面上光环的产生,再次说明背光的右半个圆周柱面的确与地面上光环(或光区)的产生完全无关。具体解释,详见图5中的图面解说1、2、3。
图6实际就是图5地面上的全部痕迹的加强版。为了方便对照,相关点字母尽量相同。其中,黑色阴影区域为金属(半)圆柱影子,用dfi和df0i(i=1、2…5)为特殊表达代表入射光线的投影虚线和反射光线的所有着地点,并用白色光区在图1(b)(c)的地面上表现出来。
3 结 论
平行的太阳光线束,照射在黑暗中站立的金属圆柱形凸面镜的半个圆周面上,会在地面上形成以圆柱体立足地为中心的光环或光区。
用作图法解析实验结果的基本原理,得到结论:(1)所有反射光线与竖直方向的夹角都相等,等高入射的反射光线在水平地面的投影长度相等,且入射平面越高,地面光环或光区的范围越大。(2)圆柱形凸面镜表面法线是沿水平方向截面圆周半径的延长线,相对于平行的入射光线,其具有对称性和高度发散性,使只照亮半个圆周的入射光线对应的反射光线着地点得以在地面形成闭合亮线,也使其地上的反射光环或光区偏离准确的圆形。
难得一遇的探究性学习,与“经验”相违背的物理真实,正是物理学的魅力所在。
致谢:图1(e)由西南大学陈志谦提供。
参考文献:
[1]D.纳赫蒂加尔, J.迪克赫费尔,G.彼得斯, 郑仁蓉. 就地取材玩物理II[M].上海:上海交通大学出版社, 2015:124.
(栏目编辑 廖伯琴)
【专家介绍】
郑仁蓉(1944-),女,PhD,教授,博士生导师。曾任西南师大物理系副系主任、西南师大副校长、全国量子力学研究会副会长等。研究领域涉及原子核结构、凝聚态和量子理论。主要从事原子核对称性投影自洽场方法、奇奇核符号因子反转、凝聚态理论等方面的研究工作。97F55C8E-96FE-4889-ABCE-291E981564C3

