太阳能辅助空气源热泵系统多地区适用性研究
王汉伟,朱 兵,吴冬梅
(1.贵州大学电气工程学院,贵州 贵阳 550025;2.贵州新能源开发投资股份有限公司,贵州 贵阳 550000)
太阳能辅助空气源热泵(SASHP)系统因其普遍适用性在国内外广泛应用[1],通过2 种不同的热源形式弥补单一供热的不足,进行多能协同规划设计[2],进而实现系统节能空间和经济效益最大化[3]。
Liu 等人[4]以高寒地区西宁市供暖季为例,将SASHP 系统和空气源热泵(SAHP)系统进行综合对比,发现前者的系统能效比(CCOP)比后者高43%,SASHP 系统的能效主要受太阳辐射的影响。曾乃晖等[5]发现在西昌地区SASHP 系统优化后,能效比(CCOPsys)普遍提高,系统全年运行费用减少,系统全年节省电能达9.11%,表明寻求SASHP 系统设备参数的最优是必要的。在曾乃晖的研究中对优化变量进行敏感性分析得到影响大小依次为:热泵功率>集热器面积>水箱容积>集热器倾角。但是在魏泽辉等[6]对SASHP 系统的研究中,最大影响参数是集热器面积,然后依次为集热器倾角>热泵功率>水箱容积。Long 等人[7]的研究结果表明,太阳能集热器面积和水箱容积是西藏SASHP 系统设计的优先考虑因素,可见热泵功率、集热器面积、水箱容积和集热器倾角等参数的影响等级并不一致。这三者分别以西昌、巴彦淖尔、拉萨作为案例地点,拉萨地区属于太阳能最丰富地区,西昌和巴彦淖尔属于太阳能较丰富地区;同时,研究中分别将全生命周期成本、太阳能平均保证率费用年值和太阳能供热比例作为目标函数:可见地区差异和目标函数的不同会得到不同的结论。
虽然广大学者研究了SASHP 系统的能耗、效能等性能参数,但同一组优化参数在多地区是否均能适用,尚须深入研究。因此,本文针对此问题研究了不同太阳能资源富集程度地区的SASHP 系统最优运行方式,并对单位制热量成本和运行能效比进行了分析,采用相对灵敏度分析了各地区不同参数的影响等级,确定了不同地区对SASHP 系统的设计思路,以期为后续研究带来一定的参考价值。
1 系统构成
1.1 地区参数
本文选取贵阳、杭州、张家口和拉萨4 个不同太阳能资源等级[8]的地区作为研究对象,其相应的气象参数见表1。

表1 4 个地区天气参数Tab.1 Parameters of weather in four regions
在12 月1 日—3 月1 日对建筑进行供暖,供热系统末端采用上侧风机盘管进行送风供暖,室内供暖温度设定为20 ℃。通常在模拟过程中,为了保持研究对象的一致性,并未对各地区的建筑围护结构作相应的修改[9]。图1 为经过TRNBuild 插件计算后的4 个地区供热负荷。
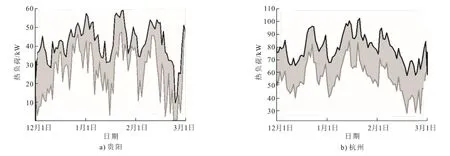
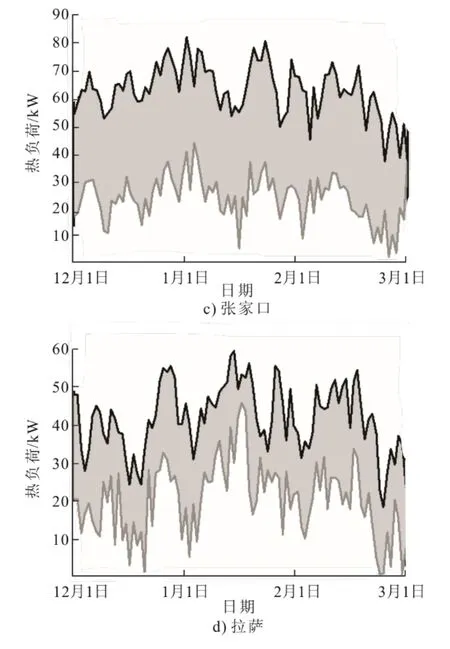
图1 4 个地区采暖季供热负荷Fig.1 The heating load of each region in heating season
由图1 可知,张家口地区热负荷变化较为稳定,而其余3 个地区存在较大负荷波动。负荷数据集整合后的极限值和累计值可为设备的约束条件计算提供依据,具体见表2。
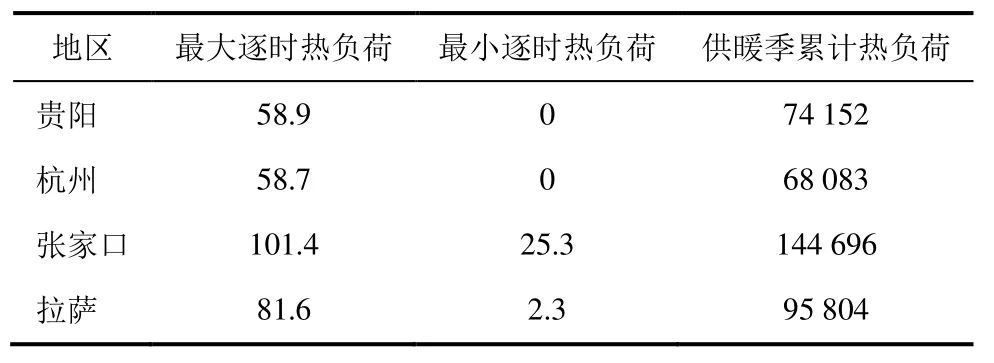
表2 4 个地区采暖季供热负荷极限值和累积值 单位:kWTab.2 The limit value and cumulative value of heating load of four regions in heating season
1.2 供热系统
图2 为SASHP 系统供热原理。由图2 可知,系统主要由空气源热泵、太阳能集热器、电辅热和蓄热水箱构成。当房间温度低于设定温度时,阀门5 打开,负荷侧水泵启动,热水从水箱送到风机盘管内进行供热,冷却后的回水进入水箱;当温度测点1(水箱温度)低于45 ℃时,集热水泵打开,由SASHP 系统进行加热。
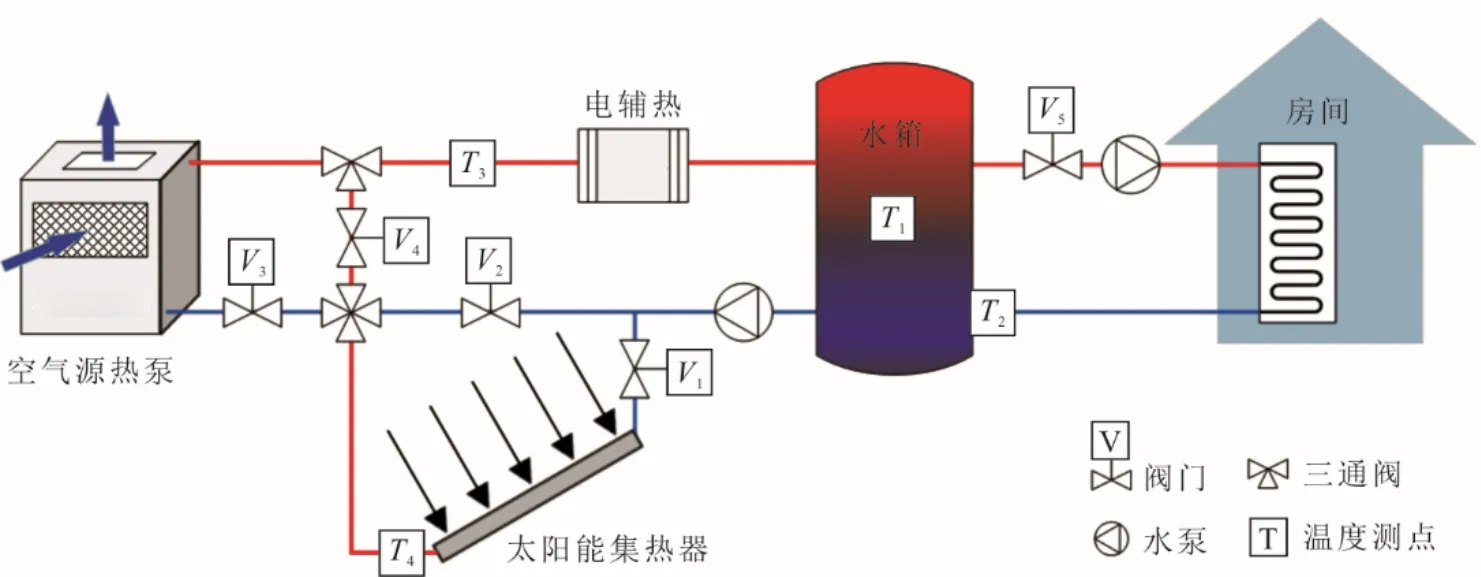
图2 SASHP 供热系统示意Fig.2 Schematic diagram of the SASHP heating system
SASHP 系统首先判断逐时太阳能辐射量,当其大于100 kJ/(h·m2)时,阀门1 打开,阀门2 关闭,冷水进入集热器内进行加热;若温度测点4(集热器出口水温)低于45 ℃,阀门3 打开,阀门4 关闭,空气源热泵启动,冷水继续进入空气源热泵内进行二次加热;若集热器出口水温高于45 ℃,阀门3 关闭,阀门4 打开,空气源热泵关闭;当温度测点3 低于45 ℃时,电辅热启动进行补热,否则关闭电加热,热水直接回到水箱中。
图3 为SASHP 系统相应的控制逻辑。图3 中:T1—T4为温度测点,对应图2 中位置;V1—V4为阀门启停信号,1 为打开,0 为关闭,对应图2 中位置;Tup为水箱设定温度,本文取45 ℃;ΔTlow为启动温差,设定温度与水箱温度之差大于ΔTlow时,进行加热,否则停止加热;ΔTup为停机温差,水箱温度与设定温度之差小于ΔTup时,进行加热,否则停止加热;Spump为水泵启停信号,Ssolar为集热器启停信号,Sashp为热泵启停信号,Saux为电辅热启停信号,启停逻辑均为1 打开,0 关闭。
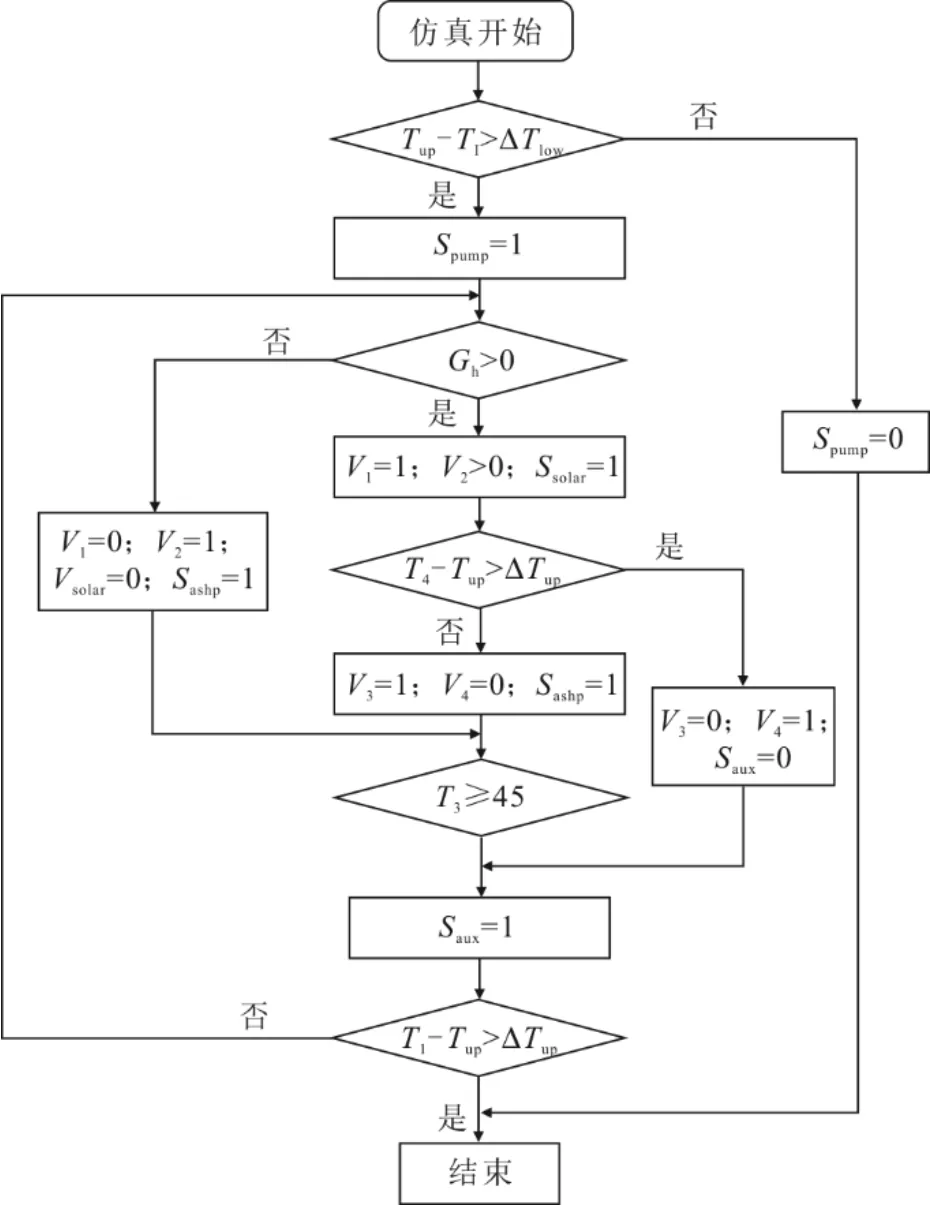
图3 SASHP 系统设备启停控制逻辑Fig.3 Start and stop control logic of device in the SASHP system
2 数学模型
本文选用TRNSYS 软件进行SASHP 系统的供热模拟,该软件更适合进行完整系统的仿真[10],用户可以通过更改外部文件的方法,达到和实际运行相近的结果。SASHP 系统中的主要模块包括空气源热泵模块TYPE_917、太阳能集热器模块TYPE_71、蓄热水箱模块TYPE_158 等。
2.1 空气源热泵
流体经过空气源热泵获得的热量和热泵自身消耗的电功率之比为热泵的效率,即能效比CCOPASHP。当不同室外温度下对应的相对湿度超过界限值时,热泵内部的蒸发器上会发生结霜,进而影响制热效率。综合考虑,空气源热泵的数学模型为:
式中:Qliq为传递给流体的热量,即空气源热泵的制热量,kJ/h;Pcompressor为压缩机功率,kW;Pblower为风机功率,kW;κ为结霜除霜损失效率。
表3 为模拟中取值逻辑[11-12]。表3 中:HRH表示空气源热泵入口空气的相对湿度,%;Ta表示空气源热泵入口空气的干球温度,℃。
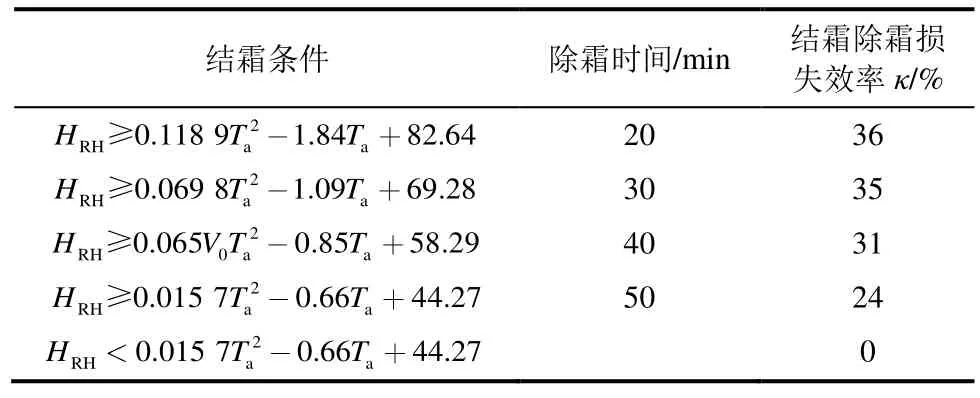
表3 不同结霜条件下融霜时间及融霜损失效率Tab.3 Defrosting cycle and frosting-defrosting loss efficiency of different frosting conditions.
2.2 太阳能集热器
本文计算模型采用HP400 真空管太阳能集热器,集热器效率为流体经过集热器的吸热总量与集热器表面的太阳总辐射之比,其数值由最小二乘法拟合集热器面积和归一化温差的瞬时效率曲线计算得到。而在实际计算中集热器的温度分布不均且难以测量,通常根据入口温度计算归一化温差,其数学模型[13-14]为:
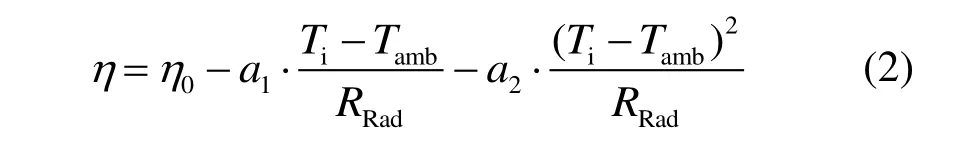
式中:η为太阳能集热器的集热效率;η0为拦截效率,本文中取0.75[15];a1为一阶效率系数,即曲线斜率,本文取1.18 kJ/(h·m2·K)[15];a2为二阶效率系数,即曲线曲率,本文取0.009 5 kJ/(h·m2·K2)[15];Ti为集热器入口流体的温度,℃;Tamb为集热器所处的环境温度,℃;RRad为投射到集热器表面的总太阳辐射,kJ/(h·m2)。
2.3 蓄热水箱
水箱是供热系统中的储热单元,同时具有平衡两侧流量的作用。蓄热水箱的热量来源一是热泵加热后的热水,二是水箱自身经太阳辐射获得的热量。蓄热水箱热量的去处是用户端消耗的热水热量和水箱自身的散热。水箱的蓄热能力为[16]:
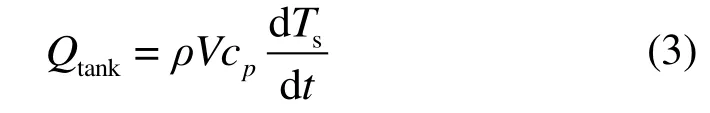
式中:ρ为水的密度,kg/m3;V为水箱的容积,m3;cp为水的定压比热容,J/(kg·℃);Ts为水温在时间t内的温度变化。
3 优化模型
3.1 目标函数
计算综合性成本时往往选择全生命周期成本CLCC作为评判参数。该参数是用于分析SASHP 系统的主要经济指标之一[17]。CLCC包括设备的初投资、设备的维护费用、设备的运行费用以及设备回收对应的剩余价值,计算公式为:
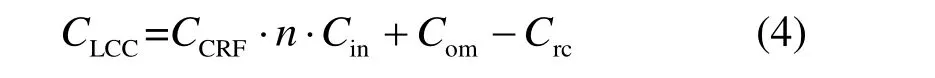
式中:CCRF为资本回收系数;n为设备寿命,年;Cin为设备的初投资,元;Com为设备的运行费用,元;Crc为设备回收对应的剩余价值,元。
资本回收系数CCRF的计算公式为:
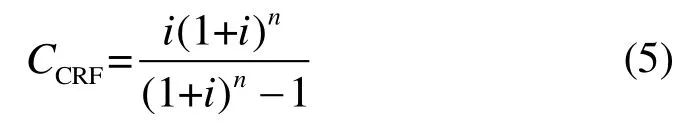
式中:i为利率,取8%[17]。
设备的初投资如式(6)所示,表4 为计算过程中SASHP 系统各装置的计算成本[1]。
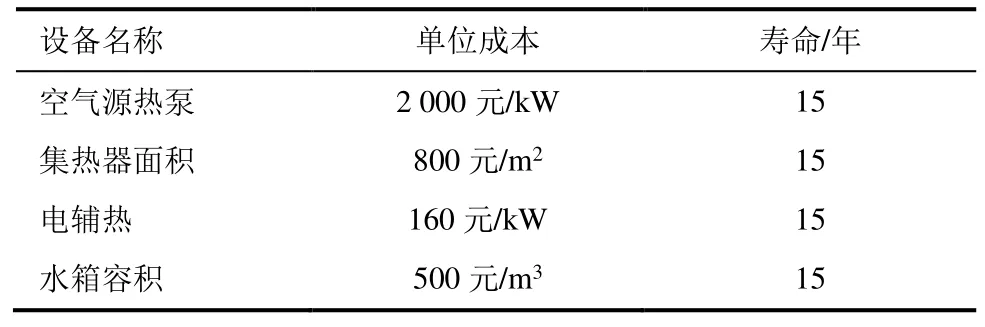
表4 各设备计算成本Tab.4 Computational cost for each equipment
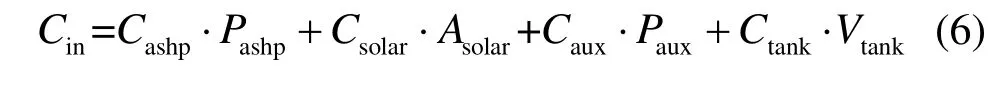
式中:Cashp为空气源热泵的单位输入功率成本,元/kW;Pashp为空气源热泵的输入功率,kW;Csolar为太阳能集热器的单位集热面积成本,元/m2;Asolar为集热器的面积,m2;Caux为电辅热单位输入功率的成本,元/kW;Paux为电辅热的输入功率,kW;Ctank为蓄热水箱的单位容积成本,元/kW;Vtank为蓄热水箱的容积,m3。
设备的运行费用包括供热过程中消耗的电量和设备维护费用,故可用式(7)表示:
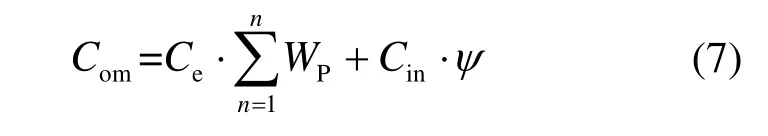
式中:Ce为电价,元/(kW·h);WP为SASHP 系统的年耗电量,kW·h;ψ为设备的维护费用系数,通常取设备初投资的2%[18]。
设备回收对应的剩余价值通常采用固定资产残值进行计算,占初投资的3%~5%[17],可用式(8)表示:

式中:r为剩余价值在初投资中的占比,本文中取4%。
3.2 优化变量
本文选择SASHP 系统中6 个重要的参数作为优化变量,分别为热泵功率Pashp、电辅热功率Paux、集热器面积Asolar、水箱容积Vtank、方位角θ和倾角β。
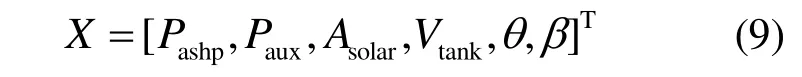
依据《太阳能集中热水系统选用与安装》[19]、《民用建筑节水设计标准》[20]、《空气源热泵辅助的太阳能热水系统(储水箱容积大于0.6 m3)技术规范》[21],优化变量相应的约束条件为:
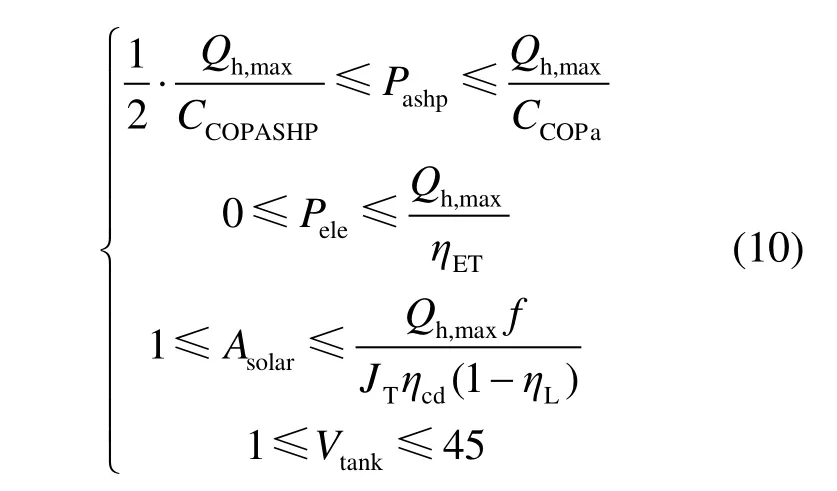
式中:Qh,max为供暖季节内建筑每小时的最大热负荷,kW/h;f为太阳能保障率,%;JT为集热器接收到的太阳能辐射总量,kW/(m2·h);ηcd为太阳能的集热效率,本文中取0.48[15];ηL为集热器的损失效率,本文取0.2[15];ηET为电辅热的热转换效率。
3.3 粒子群算法
在前人的研究[22]中,大都采用Hooke-Jeeves 算法对多参数进行优化。但SASHP 系统多参数优化问题属于典型的非线性、不可微和多极值问题,Hooke-Jeeves 算法容易陷入局部最优,即优化结果很大程度上取决于设定的初始值,而粒子群算法更适合在此类优化中寻找全局最优[23]。粒子群算法基于粒子种群的信息共享机制,每个粒子通过随机的速度和位置初始化在网格上,粒子在迭代过程中,通过追踪个体极值和全局极值,来进行所有粒子信息的相互交换,选择较优的粒子进入下一轮迭代,最终收敛于全局最优解。
粒子群算法的优化过程[24]可分为以下步骤。
1)生成数量为m的粒子组其中i∈[1,m],D为粒子群所处维度。xi为每个粒子对应的1 组优化参数,即xi为热泵功率Pashp、电辅热功率Paux、集热器面积Asolar、水箱容积Vtank、方位角θ和倾角β的方案取值。记录此时迭代次数k=0。
2)将xi代入目标函数,计算粒子组的适应度函数F(xi),即该组参数的全生命周期成本。粒子个体经过的局部最优位置记为Pbesti,整个群体粒子经过的全局最优位置记为Gbest,则:
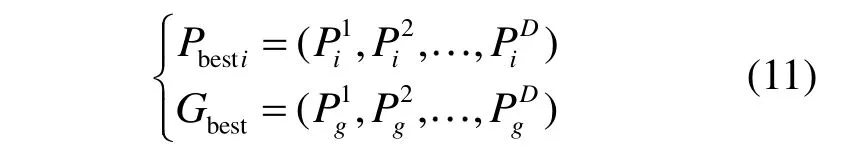
3)采用以下算法规则更新粒子的位置和速度信息,生成新一代种群xk+1,k=k+1,并计算粒子适应度F(xk+1)。
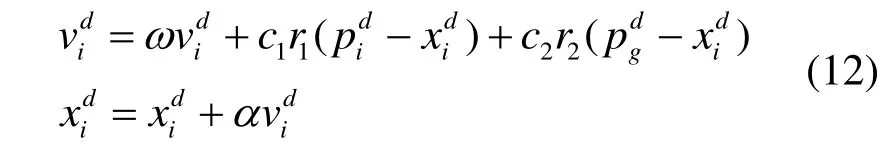
式中:d=1,2,…,D,表示第d维;r1和r2为[0,1]范围内变换的随机数;c1、c2称加速常数,是调整自身经验和社会经验在其运动中所起作用的权重;ω为惯性权重,即粒子能保持前一时刻运动状态的能力;α为收缩系数,目的是控制速度的权重。
4)比较各粒子的位置信息,更新粒子的局部最优与全局最优位置信息。
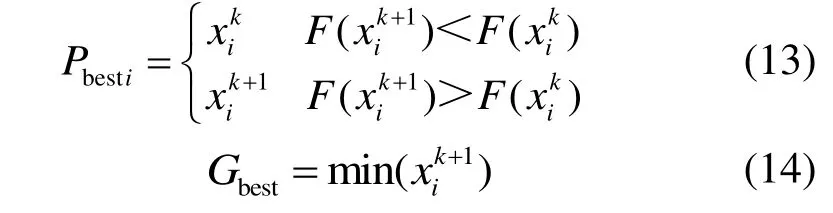
5)判断迭代次数k是否满足收敛条件,满足则终止搜索,输出最优运行方案Paux,Asolar,Vtank,θ,β],即系统最优运行的设备参数。图4 为SASHP 供热系统运行优化的流程。
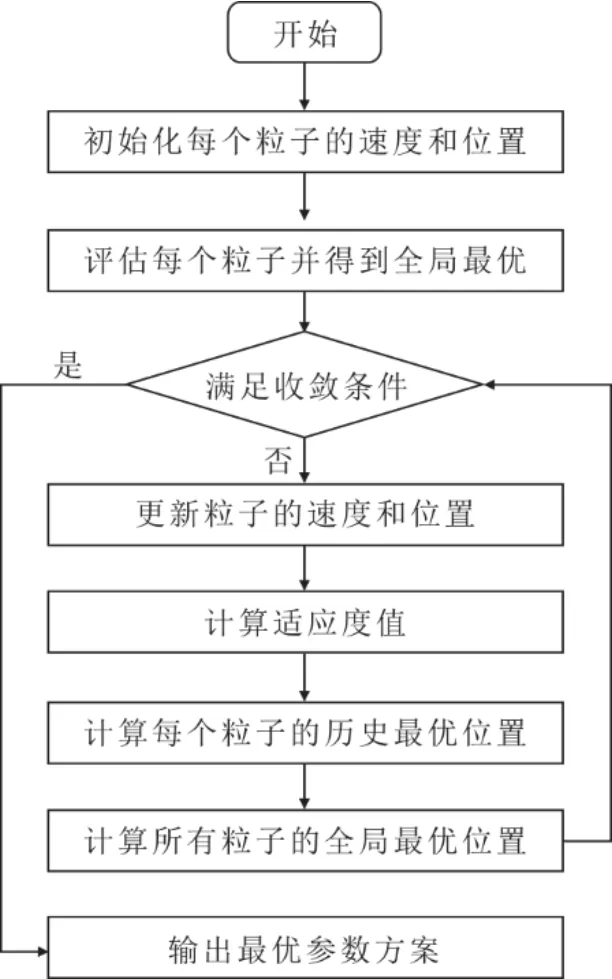
图4 SASHP 供热系统运行优化流程Fig.4 Operation optimization process of the SASHP heating system
4 仿真及结果分析
在TRNSYS 中搭建系统并设定好相应的数学模型,调用TRNOPT 插件中的粒子群算法对系统进行优化。仿真开始时,蓄热水箱中的水温设置为45 ℃,空气源热泵打开,太阳能集热器关闭,电辅热关闭。
4.1 优化结果
以CLCC为目标函数,采用粒子群算法,得出SASHP 系统最佳设备参数见表5,其中列出了4 个不同地区的供热系统优化结果。

表5 4 个地区最佳设备容量和运行参数Tab.5 The optimum equipment capacity and operating parameters in four regions
在SASHP 供热系统的设计阶段,理想情况是充分地利用太阳能,在太阳能不足时利用空气源热泵进行供热,最后用电辅热进行补热。图5 为4 个地区最佳设备参数在约束范围内的取值。
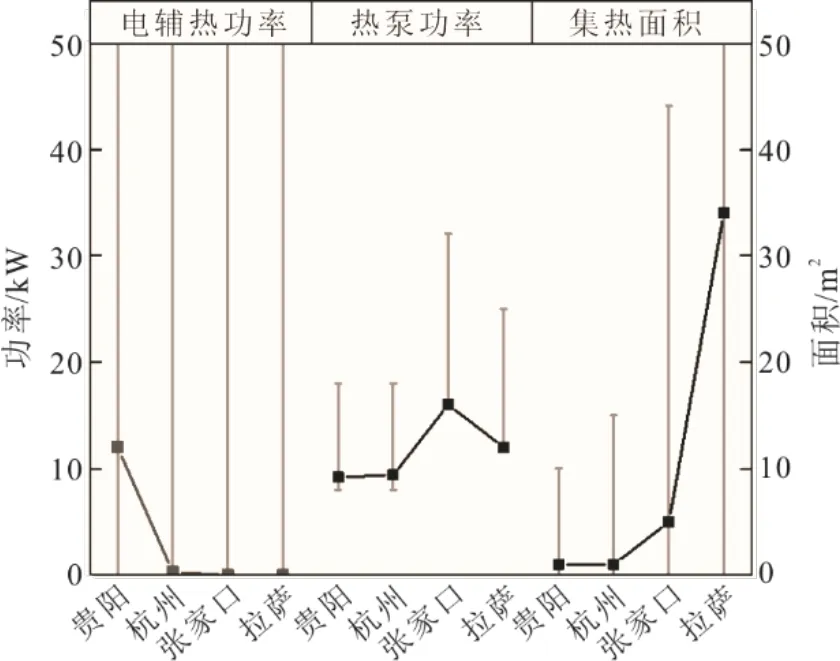
图5 不同地区最佳设备容量参数对照Fig.5 Comparison chart of optimum equipment capacity parameters in different regions
由图5 可以看出,在以空气源热泵为核心的SASHP 系统中,不同地区用以维持最小CLCC的方式大不相同。太阳能资源等级为Ⅰ级的拉萨地区和Ⅱ级的张家口地区选择约束下限的空气源热泵功率,优先增加集热器面积进行光热转换;太阳能资源等级为Ⅲ级的杭州地区和Ⅳ级的贵阳地区选择合适的空气源热泵功率,搭配电辅热进行热量的补充,其中贵阳地区需要较大的电辅热功率。供热水箱的主要作用是用于储热和调温,从表5 中可以看出,贵阳和拉萨地区最优运行方式均为小水箱。其原因是这2 个地区在供暖季的温差较小,对供热的需求无明显波动。而张家口地区在供暖季初期和后期水箱温度高于设定的存储温度(45 ℃),在供暖中期气温出现明显下降,最低温度为-20 ℃,最低温度与最高温度的温差达30 ℃,因此需要大容积的水箱进行热量的存储,以避免水箱水温处于较低温度。
4.2 经济性分析
在各地区的最佳设备容量下,各设备的CLCC占比也有所不同。图6 为不同地区最优参数下各部分CLCC占比。图6 中:LCC_KW 为SASHP 系统的年运行费用;LCC_AUX 为电辅热的初投资;LCC_VOLUME 为水箱的初投资;LCC_AREA 为集热器的初投资;LCC_AIR 为热泵的初投资。由图6可知:使用最大集热面积的拉萨地区运行费用占比(能耗占比)最少,为21%,其CLCC占比最大的部分是太阳能集热器的初投资费用,其次是空气源热泵的初投资费用;张家口地区CLCC占比最大的为空气源热泵的初投资费用,为52%,其次为水箱的初投资费用;杭州地区占比最大的为空气源热泵的初投资费用,为53%,其次为水箱的初投资费用;贵阳地区占比最大的为空气源热泵的初投资费用,为53%,其次为电辅热的初投资费用。所以进行初投资时应根据不同地区的设备初投资占比进行选择。
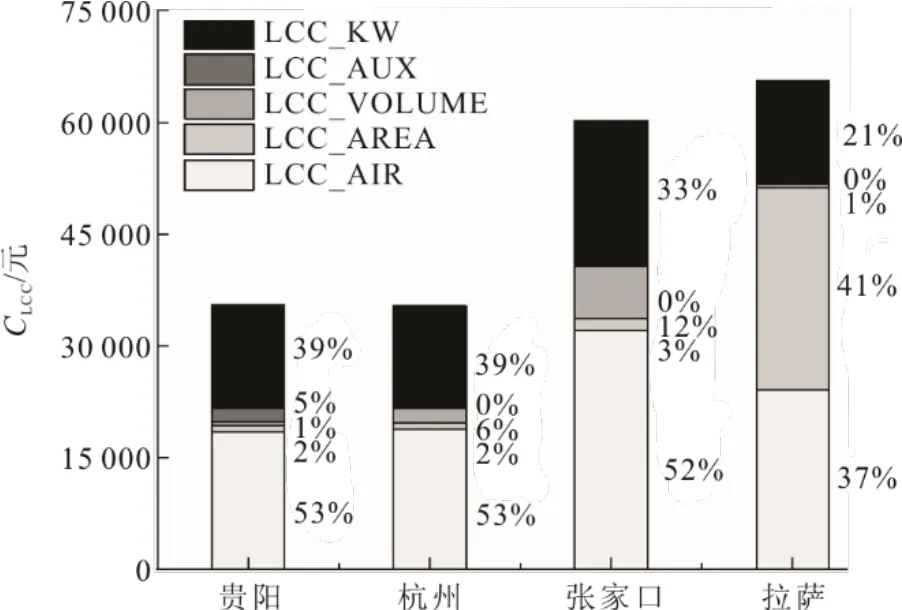
图6 不同地区最优参数下各部分CLCC 占比Fig.6 The CLCC proportion of each part with the optimal parameters in different regions
为了更准确地评判SASHP 供热系统在4 个地区的效益,选用热泵单位制热量成本CCOHASHP(热泵制热量与热泵CLCC之比)、集热器单位制热量成本CCOHsolar(集热器制热量与集热器CLCC之比)、系统单位制热量成本CCOHsys(系统总制热量与系统总CLCC之比)、热泵CCOPASHP(热泵制热量与热泵能耗之比)和系统CCOPsys(系统总制热量与系统总能耗之比)5 个指标进行对比分析。图7 为各地区单位制热量成本和运行CCOP。由图7 可知,贵阳和张家口地区的热泵单位制热量成本最低,为0.083 2 元/kW,拉萨地区的热泵单位制热量成本最高,为0.114 7 元/kW。这是由于热泵在不同地区的运行效率不同,贵阳地区的空气源热泵运行效率最高,热泵CCOP为2.94,拉萨地区的空气源热泵效率最低,热泵CCOP为2.83。太阳能集热器的单位制热量成本随太阳能资源富集程度的增加而降低,在贵阳地区最高,为3.95 元/kW,在拉萨地区最低,为0.32 元/kW。相较于其他地区,SASHP 系统的单位制热量成本在张家口地区最低,为0.48 元/kW。由图7 可知,集热器面积逐渐增大的4 个地区中,系统CCOP与太阳能富集程度成正相关,太阳能最丰富的拉萨地区系统CCOP可以达到2.26。虽然增加集热器面积会得到更高的系统CCOP,但是相应的CLCC成本显著增加,且集热器单位制热量成本远大于热泵单位制热量成本,因此,在实际的SASHP系统设计中针对不同目标应做不同的取舍。
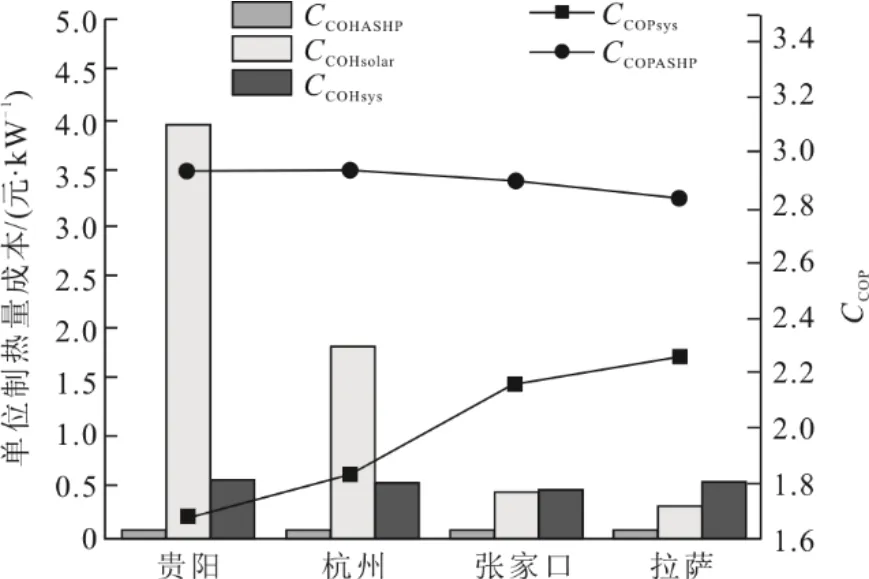
图7 4 个地区单位制热量成本和运行CCOPFig.7 The unit heat producing cost and operating CCOP in four regions
4.3 敏感性分析
为了进一步定量化分析设备容量和运行参数对CLCC的影响,对热泵功率Pashp、电辅热功率Paux、集热器面积Asolar、水箱容积Vtank、方位角θ和倾角β6 个优化变量进行敏感性分析,以期评判优化变量对CLCC的影响先后等级。本文选用相对灵敏度Si作为评判指标[25](式(15)),使各优化变量随最优值进行[10%,5%,-5%,-10%]的变化,得到相应的CLCC变化值,用以计算Si。

式中:∂(fi)为第i个优化变量引起的CLCC变化值;fiPSO为第i个优化变量最优值对应的CLCC;∂(πi)为第i个优化变量的变化值;πiPSO为第i个优化变量最优值。
图8 为各优化变量相对于系统CLCC的相对灵敏度。由图8 可知:4 个地区的热泵功率均为最高敏感等级,且远大于其他变量的相对灵敏度,说明热泵功率在最优值附近变化会导致系统CLCC大幅度增加;除热泵功率外,贵阳地区的电辅热功率具有较大影响,尽管电辅热单位设备容量成本不高,但是对能耗影响最大,即明显增加运行费用;水箱容积在杭州地区为第2 敏感等级,在其他地区为第3 敏感等级,说明热能的存储对CLCC的影响相对较大;集热面积仅在拉萨地区具有较大影响,是由于其余3 个地区均采用较小的集热面积且拉萨地区具有最富集的太阳能资源;倾斜角和方位角仅在拉萨地区影响明显,同样是由于拉萨地区需要较大的集热器面积,因此在实际的SASHP 系统运行中,应着重考虑这2 个因素,避免不必要的经济和能源损失。
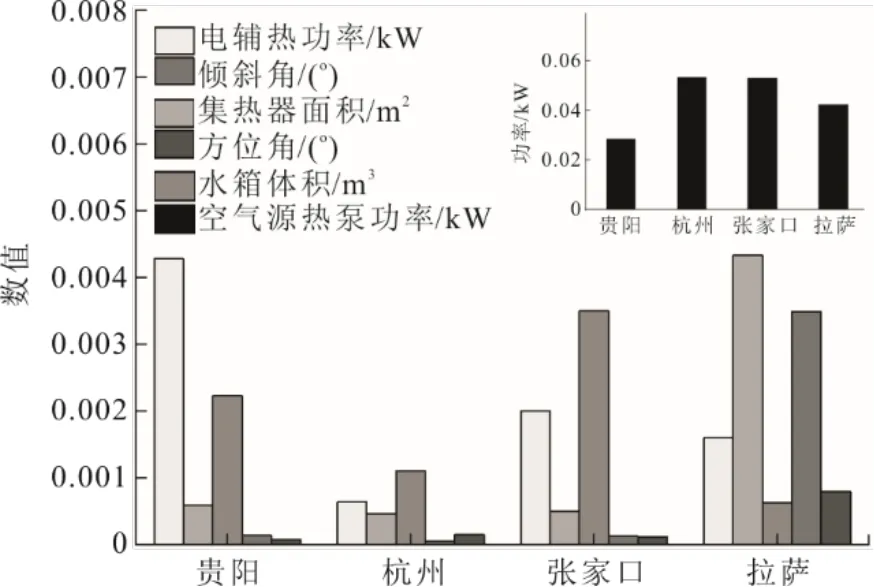
图8 优化变量相对灵敏度Fig.8 Relative sensitivity of optimized variables
5 结论
本文将4 个不同太阳能富集程度的地区作为研究对象,在TRNSYS 软件中采用粒子群算法对SASHP 系统的6 个变量进行最优化计算,并进行了经济性分析和各变量的敏感性分析。研究结果可为太阳能辅助空气源热泵系统的优化设计提供相应的理论依据。
1)从优化结果来看,太阳能资源等级为Ⅰ级的拉萨地区、Ⅱ级的张家口地区在空气源热泵的基础之上优先选择增加集热器面积;Ⅲ级的杭州地区、Ⅳ级的贵阳地区则优先选择电辅热补充热量。
2)从经济性分析来看,贵阳地区空气源热泵运行CCOP最高,为2.94,对应的热泵单位制热量成本最小,为0.083 2 元/kW;SASHP 系统的CCOP与太阳能富集程度成正相关,拉萨地区系统CCOP达到2.26,对应的集热器单位制热量成本最低,为0.32 元/kW;整个SASHP 系统的单位制热量成本主要取决于热泵的设备容量,热泵容量越大单位制热量成本越低,在张家口地区最低,为0.48 元/kW。
3)从敏感性分析来看,考虑CLCC最优的SASHP系统中,热泵功率在4 个地区均为第1 敏感等级。电辅热功率在贵阳地区有较大影响,水箱容积在杭州、张家口地区有较大影响,倾斜角和方位角在拉萨地区影响较大。

