基于无迹卡尔曼改进微分动态轨迹规划的实时算法

刘 伟, 蔡晨星, 江如海， 马利强, 李 昊

(1.安徽建筑大学 机械与电气工程学院， 合肥 230601； 2.合肥中科智驰科技有限公司， 合肥 230601)

0 引 言

在移动机器人高阶次系统轨迹规划控制中，轨迹规划受硬件与轨迹规划算法限制，导致规划结果精准性不高或实时性差。鉴于移动机器人领域对运动轨迹准确性与快速性[1]的要求不断提高，因此，轨迹规划算法依然是移动机器人领域研究的热点。

微分动态规划算法具有全局最优，二阶收敛的特点，是一种基于数值优化的轨迹规划算法[2-4]，能使用机器人系统[5]的状态和控制约束对机器人进行处理。常见的改进微分动态规划算法舍弃海森矩阵中动力学二阶导数以提高计算效率，会导致运算提前结束迭代，无法求解出最优轨迹[6-7]。动力学二阶信息决定了最优轨迹的求解效果，直接影响机器人系统执行轨迹[8]。针对微分动态规划算法在移动机器人路径规划上运算实时性不强，动力学导数计算的研究还不完善，笔者利用平方根无迹卡尔曼滤波(SRUKF)原理与拉氏定理进行近似求解，使用倒立摆模型对算法的稳定性与求解特性进行验证，在移动机器人实际运行场景下选取Z型路况对比两种算法迭代时间，验证算法实时性。

1 二阶动力学控制模型

对于高阶非线性动力学系统，通常使用运行总成本反映系统的性能与输入能量，为达到最优控制效果，可以利用运行总成本函数寻求一组最优控制输入满足系统性能要求。微分动态规划算法[2]的运行总成本为Jk，设Zk为微分动态规划算法k=N最优总成本。

Zk(x+Δx)=minu[Lk(x+Δx,u+Δu)+

Vk+1(f(x+Δx,u+Δu))]，

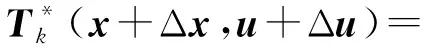
Zk+1(f(x+Δx,u+Δu))，

式中：Zk——微分动态规划算法k=N最优总成本；

Lk——中间过程代价总和；

Vk+1——最优总成本；

x——系统状态变量；

u——控制输入量。

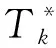
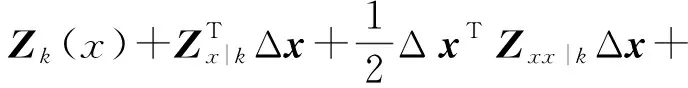
ο(ΔxTΔx)，

式中：Zx|k——最优总成本在x处的梯度；

Zxx|k——最优总成本在x处的海森矩阵；

Tx——状态梯度向量；

Tu——控制梯度向量；

Txx、Txu、Tux、Tuu——总时间成本分解后的海森矩阵块。

对海森矩阵块与梯度向量展开，展开的二阶动力学控制模型为

(1)

式中：fu——动力学控制量一阶偏导；

fx——动力学状态量一阶偏导；

fxx——动力学状态量二阶导数；

fuu——动力学控制量二阶导数；

Wk、Rk——正定成本加权矩阵；

Wk、rk——动力学控制量二阶导数。

2 动力学模型的优化求解

为求解式(1)的海森矩阵，使用Cholesky分解生成样本点为

式中：Rk——正定成本加权矩阵；

H——样本点集。

对样本点进行重排列成H=[H1,H2,H3…Hm+n]代入下列矩阵[9]：

τ=ζ2(m+n+κ)-(m+n)，

式中：τ——采样点集初始权值；

ζ——正值比例缩放因子；

β——高阶项信息参数；

λ——采样点集的缩放因子；

κ——自由调节因子。

通过以上计算，Zxx|k+1和Rk赋值状态与控制向量上并不断计算传递。在后向传递过程中，海森矩阵[9]表示为

对(1)中梯度向量进行迭代计算。式(7)中的形成的sigma点集携带了所有一阶信息[10]。利用无迹变换思想将Zx|k+1映射到用于计算海森矩阵的样本点[11-12]上进行海森矩阵计算：

(2)

由式(2)可知，根据差分定理得到线性方程组：

i=1,2…,m+n

(3)

式中：X——状态量矩阵；

U——控制量矩阵；

E——最优成本矩阵；

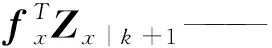
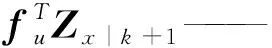
将一阶动力学导数求解值代入下式：

(4)

式(2)至(4)为海森矩阵与梯度求解过程。求解出的Δu的最小化方程控制轨迹的如下：

式中：ck——常数项；

KkΔx——线性反馈项。

将常数项与线性反馈项代入Zxx|k和Zx|k：

当成本迭代运算到k时刻时，成本预期变化为

向前递推求解出u1后结束正向递推。利用新状态控制U反馈修正计算新状态X。

在达到收敛条件[11]前不断重复上述过程，最终达到局部最优。

3 倒立摆系统的仿真

为验证文中提出的无迹微分动态规划算法的可行性，进行倒立摆系统仿真实验[13-15]。仿真流程如下，联立倒立摆模型的非线性动力学方程与代价函数，在Matlab软件中求解。计算运行价值的海森矩阵及一阶导数，计算最优的控制量与状态量之间的关系式。求解X、U及ΔJ，判断ΔJ是否满足误差，当ΔJ满足误差时输出最优控制轨迹u并结束运行；若ΔJ不满足条件，减小α值并返回至非线性倒立摆动力学方程。

3.1 控制效果评估

两种算法在倒立摆仿真系统的控制量变化与总成本变化如图1和2所示。由图1可知，两种算法的控制量保持一致，表明新算法保留了原算法的规划控制特性。

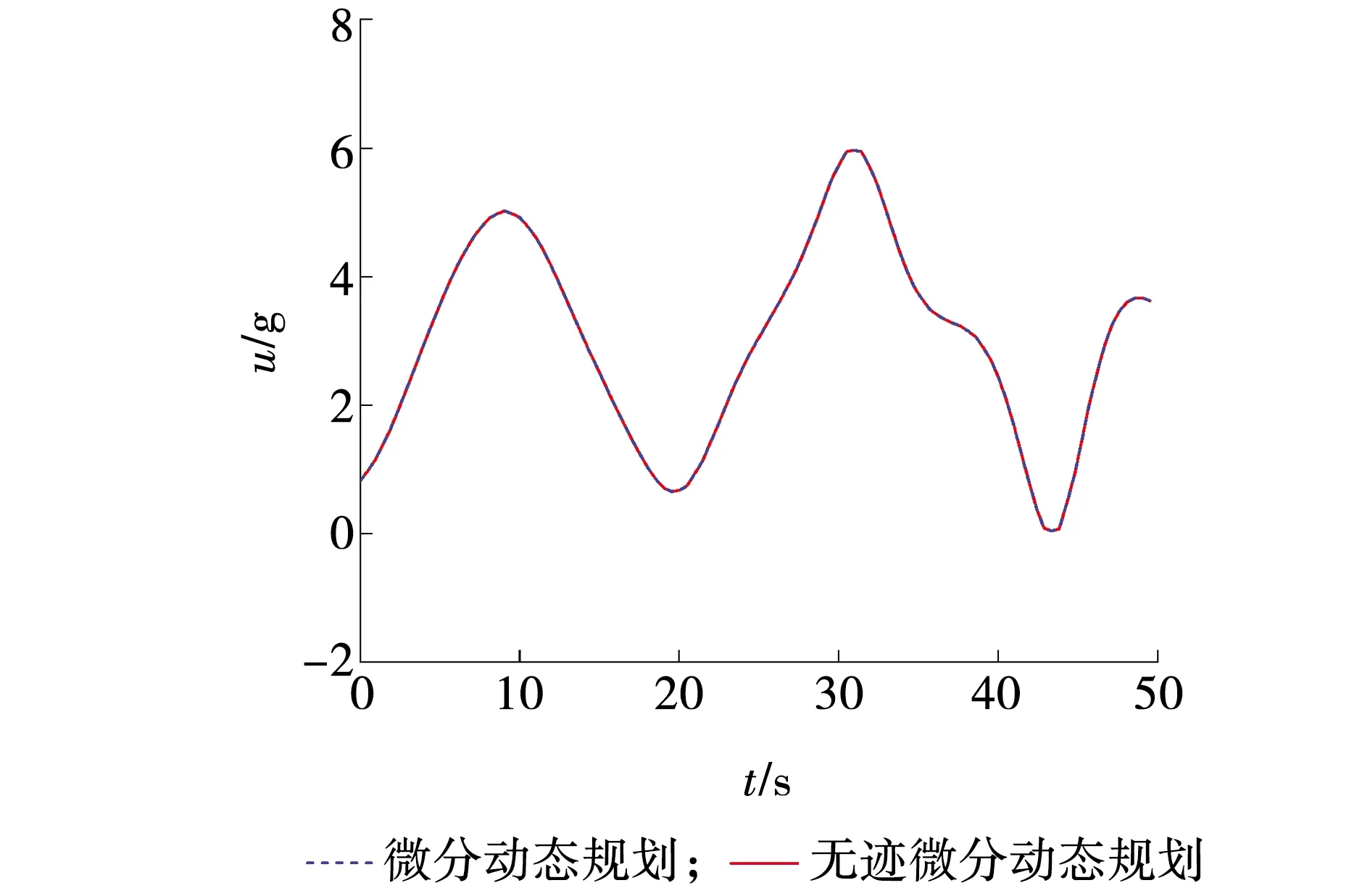
图1 算法控制量变化Fig. 1 Algorithm control quantity change

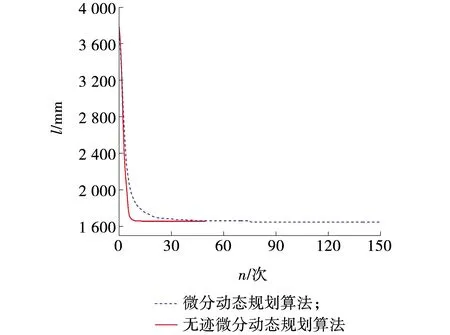
图2 规划总成本变化Fig. 2 Total planned cost change

对比两种算法规划成本变化，新算法与原算法的总成本都从3 780 mm降至1 643.77 mm。两种算法初末总成本量保持一致。无迹微分动态规划算法在单次迭代上更容易往最优区域搜索，成本减小量高于微分动态规划算法，但最终收敛成本与微分动态规划算法相同，表明无迹微分动态规划算法控制成本压缩性一致。

3.2 实时性评估

两种算法单次迭代时的具体数据见表1。无迹微分动态规划算法的总成本lw下降速度更快，选取第3次、第5次和第7次迭代结果，无迹微分的总成本量分别为2 585.2、1 960.6和1 694 mm。

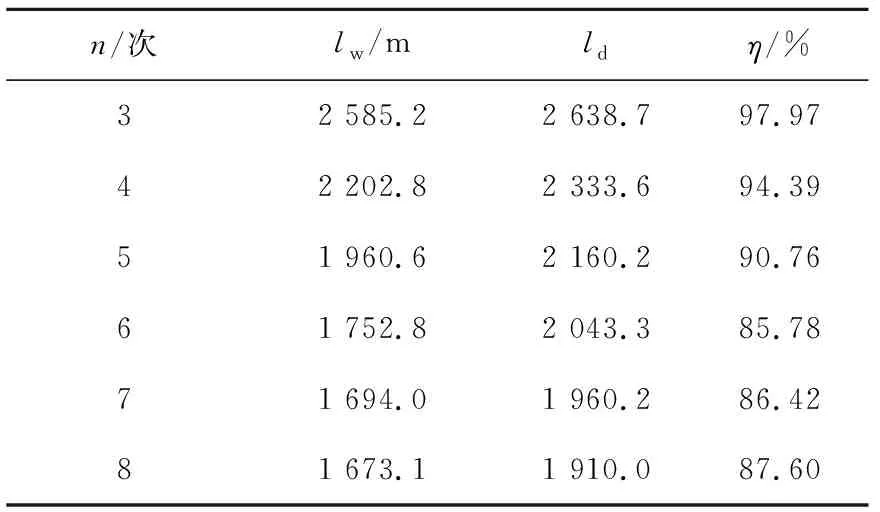
表1 单次迭代数据Table 1 Single iteration data

与微分动态规划算法同次迭代结果相比，总成本量为微分动态规划算法总成本ld量的97.79%、90.76%和86.4%。三次迭代结果对比，无迹算法总成本比微分算法总成本分别压缩2.21%、9.3%和13.6%。新算法单次迭代的压缩效率更高，能有效减少迭代时间，提高微分动态规划算法的实时性。

倒立摆模型运行结果如表2所示，两种算法的最终成本量一致，优化算法的单次迭代运行时间为440 ms，单次运算时长为微分动态规划算法的48.73%，单次迭代运算效率提升51.27%。优化算法总运行时间为23.35 s，原算法运行时间为135.39 s，总运行时间效率提升了82.75%。综上分析，优化算法的实时性优于原算法。

表2 倒立摆模型仿真运行结果Table 2 Simulation results of inverted pendulum model

4 实验验证

为进一步验证优化算法在实际应用中的实时性，将文中算法应用到XL4301轮式移动实验平台，实验平台搭载GPS系统，采用北科天绘激光雷达以及上位机。

4.1 移动机器人动力学建模

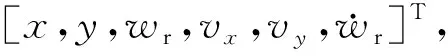
表3 移动机器人参数Table 3 Parameters of mobile robot

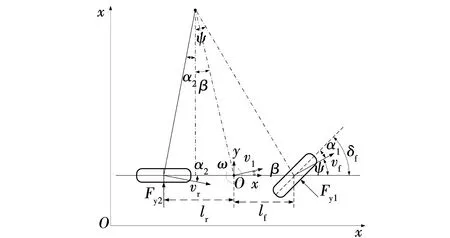
图3 动力学模型Fig. 3 Dynamic model

机器人动力学模型公式为

4.2 实验方案设计

实验原理：设置Z型实验道路，经两种算法求解后获得最优轨迹，发布虚拟轨迹节点。虚拟轨迹节点生成后经VCU节点转换为控制命令，电机接收信号运转，轮式机器人运行。利用GPS与惯导记录相应的数据与信息，对比每次实验的算法运行的总时间与机器人运行轨迹，分析算法实时性与控制特性。实验场景如图4所示，选取Z字型路况，Z字型弯道路况包含两个转角，全长40 m。

图4 道路轨迹Fig. 4 Road trajectory

4.3 Z型路径实验与验证

Z型道路实际运行的控制参数变化如图5所示。第一段直线加速过程前轮转角与转角加速度不变，速度上升到最大。第二段速度降低，加速度先减小后回落至0 m/s2，前轮转角先上升再降低至0°；第三段速度、加速度、前轮转角与前轮转角导数均无变化；第四段路程前轮转角先下降后上升，轮转角导数先下降再上升最后回归到0 (°)/s附近。第五段速度上升，轮转角与轮转角导数均不变。前轮转角最大值为30°，最小值为-30°；前轮转角导数最大值为11 (°)/s，最小值为-11 (°)/s。

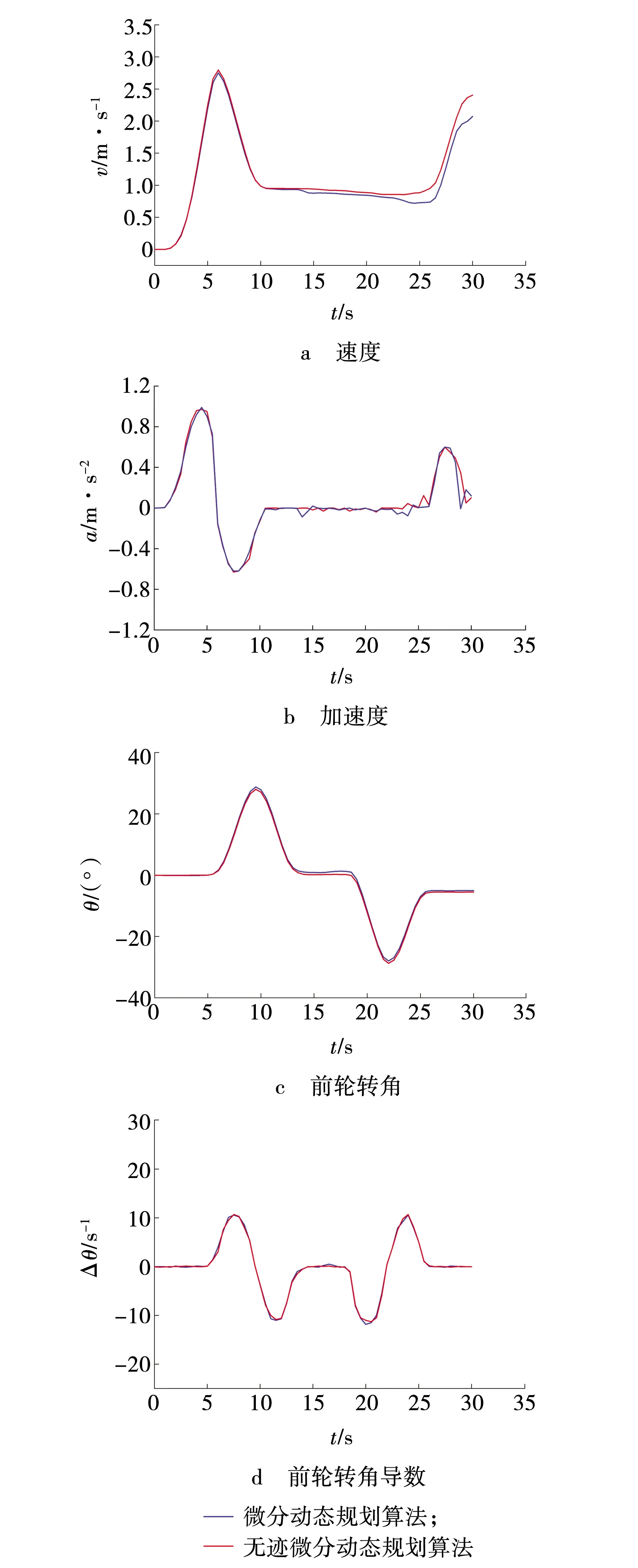
图5 道路运行结果Fig. 5 Road operation results

Z型路况最为复杂，包含两处较大转角，Z型路径规划原算法总用时为3.44 s,优化算法规划时间为2.16 s，相较于微分动态规划算法新算法运行效率提升了37.2%。

对比无迹微分动态规划与微分动态规划实际运行结果，二者规划结果从实际控制量来看基本保持一致，控制量算法上两种算法运行结果极值相同；相同时间段内两者控制量曲线剔除实际道路对数据的影响趋向相同。两种算法计算控制轨迹结果相同，说明新算法可以保留原算法特性。

优化算法在Z字型道路实验中求解时间较原算法缩短了37.2%。实验分析得新算法比微分动态规划算法有更高的实时性，且遇到大转角复杂情况时优化算法有更好的实时性。优化算法运行总时间相比于原算法运行总时间更短。因此，可以得出在实际路况，优化算法比原算法实时性更好。

从仿真实验得出，两种算法从控制量到压缩成本量上均保持一致，在实时性上无迹微分动态规划算法收敛性更好，能更快完成成本压缩，具有更高的实时性；从实际道路实验可得两种算法在实际控制效果基本保持一致，实际道路求解实时性均高于微分动态规划算法，道路实验验证了仿真结果的正确性。

5 结 论

(1) 分析了微分动态规划算法动力学信息求解过程，建立了二阶动力学控制模型，引入无迹变化构建动力学样本点与差分思想求解梯度与导数，优化了动力学模型中海森矩阵与梯度计算方法。

(2) 通过倒立摆仿真与Z型路况实验对比分析了两种算法迭代时间，仿真环境下优化算法总运行时间效率缩短了82.75%，单次迭代运算时间效果缩短了51.27%，在实际道路测试中改进算法求解性能提高了37.2%，无迹微分动态规划算法实时性优于算法。