改进遗传算法的救援机器人路径规划

赵 杰， 王馨阳， 王 贺

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

自然灾害的发生会造成很大的人员伤亡以及经济损失，为挽救生命财产，提高救援机器人[1]的救援效率，目前，已成为国内外机器人控制领域[2]的重点研究方向。因此，使其迅速地抵达受灾后地点进行援助，规划一个有效、无障碍和最短安全的路径对提高救援效率是至关重要的[3]。

研究相关机器人路径规划的学者较多，Zanlongo等[4]应用RRT和A*算法设计出由操作员控制多个机器人的方法，但是该方法中算法搜索速度较慢，可能陷入局部最优。Rogonondo等[5]应用VFH+算法，给出能探索未知环境的机器人路径规划的方法，但其存在避障时左右徘徊、阈值敏感及增加搜索时间等缺点。Zafar等[6]结合GWO和APF算法，设计了改进GWO算法，确保在容易出现障碍物的场景中无碰撞优化路径，但所使用的障碍物模型较简单，不具有普遍性，搜索时间较高。Lu等[7]提出的A*算法，结合图像处理和激光传感器，可以在未知环境下得到所需目标的最短路径，但需要处理大量的图像信息，搜索效率低、路径不平滑等缺点。针对目前救援机器人路径规划研究的现状，在救援机器人路径规划中采用遗传算法，对该算法搜索较慢、局部搜索差及不能保证算法收敛，以及用于救援机器人路径规划时，其得到的路径长度较长，路径拐点多等问题，笔者提出一系列策略改进遗传算法，通过仿真实验验证改进算法的搜索效率，以提高救援机器人救援能力。

1 栅格法环境建模

环境建模是对救援机器人实际的运动过程中所经历的环境信息的构建，在救援机器人寻优路径时就是要先将环境信息由实际形式经过连续处理变成为符合路径寻优的虚拟形式，而最为关键的是怎么表现障碍物。合理的，有效的建模才可以使寻优路径中的信息量减少，才可以有助于减少时间。各种各样的路径规划方法是基于不同的建模方法来进行的。

栅格法构建的地图模型不仅可以直观有效地表示现实环境中的信息，而且其是由矩阵数组表示的，从左到右，从下到上每一个小方格，与遗传算法的种群个体一样都是用实数编码的，运用遗传算法在栅格地图中规划路径，有助于选择、交叉、变异的操作，因此，文中选择栅格法建立模型。

为方便计算，将救援机器人看作运动的质点，模型中障碍物已知其位置，并不会改变。构建栅格地图时，其方格范围将影响实际信息描述，设备存储和算法寻优搜索时间。文中建模的范围是 20 m×20 m，对表示障碍物的方格取值1，表示无障碍物方格取值0，并在Matlab仿真软件中得出如图1的栅格环境模型。

图1 栅格的环境模型Fig. 1 Grid environment model

由图1可见，黑色代表障碍物，白色代表可以行走通过[8]。用(x,y)来表示栅格位置，单位为m。起点为(Xs,Ys),终点为(Xe,Ye)，设栅格编号(1,1)为0，(20,20)为399。栅格坐标(x,y)和编号n(n的取值范围0～399)的关系为

x=mod(n,20)+1，
y=fix(n/20)+1，

式中：mod——取余运算；

fix——取整函数。

2 遗传算法的改进

2.1 传统的遗传算法

遗传算法具备较好的全局搜索能力，尤其是在复杂环境下的优化问题中的搜索能力和稳定性。应用于救援机器人的路径规划基本思想是：首先将所求函数的所有解(所有的路径)视为种群中每一个体，所有个体用实数编码，视为基因，然后采用选择、交叉和变异[9]依次进行寻优，进而对种群优化，选择出更适应环境模型的下一代群体。寻优路径过程中，可以将所有可能的路径视为种群中的个体，假若群体中总共是n个个体(相当于n条路径)，另外，每个个体中有m个基因(相当于中间含有地图方格节点数量)，最后通过一代一代的进化，对种群进行三个遗传算子的操作，选择出最合适的个体，即最优路径。

2.2 改进的Sine混沌映射初始化种群

遗传算法，在求解救援机器人的路径规划的问题时，在迭代后期种群的多样性会减小，容易陷入局部最优解当中，导致收敛准确度下降，不能得到最优路径。为提高算法的搜索能力，避免迭代后期种群多样性减小，考虑到混沌映射中，具有随机性、遍历性、规律性优点，而Sine混沌映射与其他混沌映射相比较简便，保证了更高的随机性、遍历性、规律性和安全性。

传统的混沌映射中，正弦函数具有非常重要的地位，而且均与其自身相关。Sine混沌映射是以正弦函数为基础的混沌映射[10]。正弦映射是一种动态的系统[11]，定义为

yn+1=βsin(πyn)，

式中，β——控制参数，取值范围0.87～0.93。

一般当β取值在0.95～1时会有混沌现象，但是产生该现象的区间中有可能会有混沌现象消失的部分，只有当β无限趋于1时，混沌现象才会越好。

Sine混沌映射的构造虽然简单，但迭代的序列容易被预测到，混沌序列的直方图如图2所示。Sine混沌映射在[0, 0.05]和[0.95, 1]的取值概率要远远高于其他各区间的取值概率，呈现出两头大中间小，各段的值相差大的现象，分布不均匀，控制参数β范围小等缺陷，影响了算法在寻找最优路径的速度和精度。

图2 Sine混沌序列直方图Fig. 2 Sine chaotic sequence histogram

文中设计出一种改进型Sine混沌映射为

(1)

式中：mod——取余运算；

rand——生成(0,1)之间的随机数；

a——控制参数。

其混沌序列的直方图如图3所示。其用于初始化种群。

图3 改进型Sine混沌序列直方图Fig. 3 Improved sine chaotic sequence histogram

由式(1)可得改进型Sine混沌序列，遗传算法的初始化种群由yn+1经式(2)进行线性变换可得：

pi=lb+(ub-lb)yn+1，

(2)

式中：lb——变量空间下界；

ub——变量空间上界。

比较图2和3可以发现，改进型的Sine混沌映射在[0,1]间有更好的遍历性和规律性，分布更加均匀，而且控制参数a的取值范围是任意实数。改进型Sine混沌映射相对于传统的Sine混沌映射性能更加优秀，用于初始化遗传算法种群可以使其更加均匀地分布于初始解空间，文中最后用改进型的Sine混沌映射进行遗传算法种群的初始化。

2.3 适应度函数的设计

种群个体是否为精英个体取决于适应度函数值大小，即决定了个体的生存能力。其值高时容易存活，低时就会死亡，因此，可作为判断个体的优劣的标准[12]。在传统遗传算法的应用里，通常用路径长度为适应度函数，虽然其结构简单便于计算，但是规划的路径中通常拐点数量较多，尤其在一些转弯角度较小的拐点中，容易使救援机器人移动救援过程中造成安全问题，路径规划效率也会大幅降低。

针对传统路径长度适应度函数存在的问题，为更好判断种群个体的优劣，文中提出了一种适用于救援机器人路径规划的适应度安全评价函数Te，其对遗传算法寻找最优路径的效率和精度有巨大的影响。Te包含了路径规划中的路径长度f1和路径平滑评价度f2，Te函数为

Te=mf1+nf2，

式中：m——f1权重；

n——f2权重；

(xi,yi)——路径点i节点坐标;

(xi+1,yi+1)——路径点i+1节点坐标;

M——路径中节点的数量。

由于转弯的角度不能太大，因此，救援机器人转弯时应有合适的惩罚权重，降低转弯概率。文中利用余弦定理、cos函数及arccos函数三者依次来判断转弯角度及设置相应的转弯角度及对应的惩罚权重为

b=(xi-xi+1)2+(yi-yi+1)2，

c=(xi+2-xi+1)2+(yi+2-yi+1)2，

a=(xi-xi+2)2+(yi-yi+2)2，

w=arccosA，

Ai=Ai-1+α，91Ai=Ai-1+γ，47Ai=Ai-1+ε，w≤47，

式中：xi+2、yi+2——路径点i+2节点坐标;

α、γ、ε——转弯角度对应的惩罚权重。

α、γ、ε按照栅格环境模型中的黑色和白色栅格的数量和位置来取值。当模型范围较大或黑色栅格较多，分布复杂时，应当选取较大的值，区分出种群个体中的高、低适应度值的个体来。权重m、n根据模型的复杂程度和路径实际特点进行取值，为下一步进行一系列遗传操作奠定基础。

为验证文中所提出的适应度安全评价函数Te的优越性，对遗传算法分别以传统路径长度为适应度函数和以安全评价函数Te为适应度函数，进行两组仿真实验。算法的主要参数设定为：种群数量200，pc=0.9，pm=0.2，α=3，γ=15，ε=20，最大迭代次数Mg=70。从两组仿真实验得出，以传统适应度函数的路径中转弯的平均次数是17次，以Te为适应度函数的路径中转弯平均次数是12次。

由传统适应度函数的路径图4和以Te为适应度函数的路径图5中可以看出，以Te为适应度函数的路径更光滑平稳，路径转折次数大为减少。因此，文中所采用的安全评价函数Te作为适应度函数减小了转弯的概率，提高了救援机器人移动路径的平滑程度，平均提高了29.41%，增加了救援工作的安全效率。

图4 传统适应度函数的路径Fig. 4 Path of traditional fitness function

图5 Te为适应度函数的路径Fig. 5 Path with Te as fitness function

2.4 遗传的自适应选择操作

蚁群算法基本原理：在初始种群随机走过路径的概率是相同的，通过在走过的路径上分泌信息素的方式，另外并将信息反馈给种群。其在路径上越多，其他个体走这个路径的可能性越大，而该算法的种群是在未给予任何信息的情况下找到一条从初始节点到最终节点之间最短路径[13]，而信息素最多的路径就是最短路径。

应用改进Sine混沌映射进行遗传算法种群的初始化后，选择个体时，高适应度的路径有未被选中的可能性。因此，为降低此类情况发生的概率，文中根据蚁群算法的原理和轮盘赌算法，得出文中改进算法自适应选择操作：首先，文中设计一个自适应选择算子因子Pi，如式(3)所示，其次，按照自适应选择算子因子Pi将路径(种群个体)分为高适应度路径(精英个体)、 低适应度路径(非精英个体)，从低到高排序，然后，通过rand随机数判断选择哪条路径时，会降低选择低适应度路径的可能性，增加选择高适应度路径的可能性。路径适应度值越大，选择该路径的可能性就越大。

(3)

式中：Tei——第i代路径的适应度；

Mg——最大迭代次数；

η——适应度重要程度因子。

η的Sigmoid激活函数为

虽然该方法能快速选择种群适应度较高的个体，提高算法收敛速度，但其会降低种群的多样性，可得到局部较短路径。因此，文中通过非线性交叉操作和线性变异操作防止陷入局部最优，使种群维持较高的适应度，不会降低种群的多样性，并向更好更优的方向进化。

2.5 非线性交叉与线性变异操作

交叉操作选用单点交叉[14]。其是指如果搜索到的路径中，有两个路径(两个种群个体)存在相同的节点或多个相同的节点，则根据交叉概率pc判断是否将这两个路径作为父代执行交叉操作；若进行交叉(随机选择相同的节点进行)，则交叉后留下较短的路径。在进行交叉操作后，下一代个体的适应度可能大于父代的，从而寻找最优路径。

变异操作在寻优过程中将已知的上一代个体以变异概率pm在某一节点随机性向各方向临近节点进行突变，其有可能会出现变异之前路径无障碍物，变异之后路径有障碍物，增加了障碍路径产生的概率。为解决这问题，文中采取的方法是，在某一路径进行变异操作后，判断变异后是否为障碍路径，若是则删除这条路径，取消变异操作；若不是则保留。例如，在图6中，假设路径为[1 6 11 12 16]，随机突变在6号栅格；那么突变的可能性就如图6中的箭头所示，当突变后的路径有5号栅格，就删除这条路径，取消变异操作。

图6 变异操作Fig. 6 Mutation operation

改进遗传算法的流程如图7所示。经典遗传算法的pc和pm一般是固定不变的，但是这容易增加破坏适应度高的路径概率，降低种群的多样性，对种群的产生有害进化。因此，引入SoftSign激活函数的导数设计出了非线性交叉操作，公式为

图7 改进遗传算法的流程Fig. 7 Improved genetic algorithm process

式中：pcmax——交叉概率上限；

pcmin——交叉概率下限；

i——当前迭代次数。

结合非线性交叉操作可能得到适应度更高的下一代个体(路径)，但有可能在迭代后期降低种群的多样性。而在变异操作中，假如pm较小，则会有路径不突变的可能性，且降低种群的多样性，算法的搜索能力减小，但pm不能太大，否则突变的路径变多。虽然极大增加了种群的多样性，但不利于全局搜索；因此，文中在非线性交叉操作之后，又设计出了线性变异操作如式(4)，能使算法尽可能较多地寻找到个体(路径)，有利于其逃离局部最优解，提高迭代后期的种群的多样性。

(4)

式中：pmmin——变异概率下限；

pmmax——变异概率上限；

p1、p2——变异概率的因子。

3 仿真结果与对比分析

为验证所提出的理论和改进的遗传算法，在Matlab仿真软件下进行实验。分别对遗传算法、改进的算法和蚁群算法，在简单地图和复杂地图中，并改变起点和终点的坐标，进行2组仿真对比。

文中算法的主要参数设定为：种群数量200，a=64，lb=-100，ub=100，m=n=1，α=3，γ=15，ε=20，pc_max=0.9，pc_min=0.3，pm_max=0.8，pm_min=0.2，最大迭代次数Mg=70。

经典遗传算法的种群数量，最大迭代次数与文中算法的一致，而pc和pm的取值分别为0.9和0.2。为便于比较两个算法，在两个算法中均以Te为适应度函数。极大提高了救援机器人的救援能力和在复杂地图中搜索效率的有效性。为进一步验证改进的遗传算法，与蚁群算法救援机器人路径规划进行对比。第一组仿真实验，简单地图的障碍物覆盖率为21%。

由仿真实验结果图8和9，以及表1的对比数据可得，改进的遗传算法与经典遗传算法相比，最优路径长度平均减小了5.24%，收敛速度提高了30.00%，搜索时间平均减少了3.54%；与蚁群算法相比，虽然两者的最优路径长度相差不大，但前者搜索效率更高，收敛速度提高了46.15%，搜索时间平均减少了88.50%，文中算法极大提高了救援机器人的救援能力和在复杂地图中搜索效率的有效性。

图8 简单地图中三个算法的路径规划Fig. 8 Path planning of three algorithms in simple map

表1 简单地图中算法仿真结果Table 1 Simulation results of algorithm in simple map

图9 简单地图中三个算法的路径收敛曲线Fig. 9 Path convergence curves of three algorithms in simple map

为更一步的证明文中算法的优越性，在更复杂的地图中进行仿真实验。仿真结果如图10和11所示。第二组仿真实验，复杂地图的障碍物覆盖率为28%，并改变起点和终点的坐标。

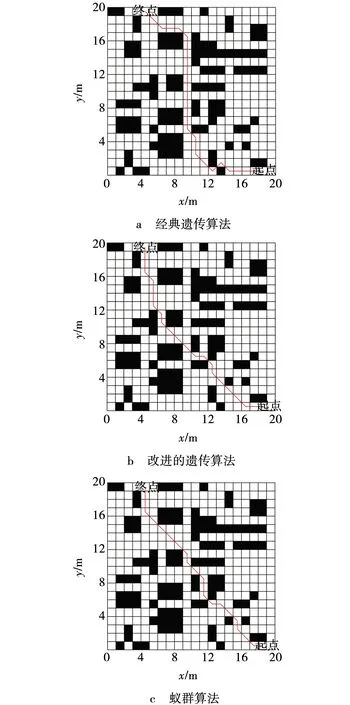
图10 复杂地图中三个算法的路径规划 Fig. 10 Path planning of three algorithms in complex map

图11 复杂地图中三个算法的路径收敛曲线Fig. 11 Path convergence curves of three algorithms in complex map

根据仿真实验图10和11，以及表2的对比数据可得，在复杂地图中改进的遗传算法与经典遗传算法相比，最优路径长度平均减小了2.16%，收敛速度提高了27.08%，搜索时间平均减少了4.01%；与蚁群算法相比，收敛速度提高了37.50%，搜索时间平均减少了91.67%，在更复杂地图中，虽然两者的最优路径长度相差不大，但平均搜索时间减小幅度比在简单地图中更大，这证明了文中改进遗传算法在更复杂，更困难的环境中缩短在救援时间上的优越性。

表2 复杂地图中算法仿真结果Table 2 Simulation results of algorithm in complex map

4 结 论

(1)为了使救援机器人更好快速地到达救灾现场进行救援，文中提出了改进的Sine混沌映射、自适应选择、非线性交叉与线性变异操作，设计了带有惩罚权重的适应度安全评价函数Te，增加了机器人路径的平滑程度策略改进了遗传算法。解决了算法在寻优中存在种群多样性低，易选择低适应度的路径，陷入局部最优，且在迭代后期寻优速率慢等问题。

(2)通过改进遗传算法分别与经典的遗传算法和蚁群算法的仿真实验对比，在两种地图中与蚁群算法相比，救援时间分别减少了88.50%，91.67%，证明了文中改进遗传算法更适用于复杂、困难的环境中。