基于优化的增程式电动汽车能量管理策略

王 勇，汤 赐，肖 宁，刘 智，杜 涵

（长沙理工大学电气与信息工程学院，长沙 410114）

0 引言

化石能源的日益枯竭和大气环境的污染是21 世纪工业发展面临的重大难题，由于传统汽车大量使用化石能源以及排放污染气体，新能源汽车的研究越来越受到重视［1-4］。增程式电动汽车是一种介于纯电动汽车和传统汽车的车型，兼具了两者的优点，没有复杂的驱动结构，并附有增程器，其可实现低排放、强续航能力目标［5-7］。

合理的能量控制策略可以提高整车的动力性及经济性，目前对于增程式电动汽车，主要有恒温器型控制策略、功率跟随型控制策略以及恒温器+功率跟随结合的控制策略［8-10］，文献［11］设计了发动机三点控制策略，并利用非支配排序遗传算法对参数进行了优化，降低了燃油消耗；文献［12］提出一种基于自适应神经模糊推理系统的增程式电动车多工作点能量管理策略，降低了系统开发时间；文献［13］以行程结束时电池的SOC 处于较低水平为目标，提升了增程器的燃油经济性。本文从提升动力电池寿命角度出发，引进了超级电容，设计了粒子群算法（PSO）优化的双模糊控制策略，并仿真验证了所提策略的有效性。

1 动力系统架构

1.1 汽车顶层架构

传统的增程式电动汽车主要包括电动机、发电机、动力电池、发动机等几个主要部件［14］。

电池寿命主要与电池的充放电倍率、充放电循环次数、电池温度等有关，而在传统的增程式电动汽车中，动力电池来承担瞬时峰值功率，以及频繁的回收能量，这大大影响了电池的使用寿命。超级电容具有更高的比功率，能够承受动力电池过充过放的功率，引入超级电容后，能够提升电动汽车比能量与比功率兼备的整体性。超级电容的拓扑主要分为全主动、半主动、被动3 种构型，综合考虑各结构的使用效果和控制难易程度，本文采用半主动式连接，如图1 所示。

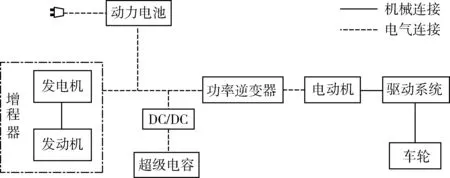
图1 增程式电动汽车基本结构Fig.1 Basic structure of incremental electric vehicle

1.2 工作模式分析

增程式电动汽车的整车需求功率计算公式为［15］：

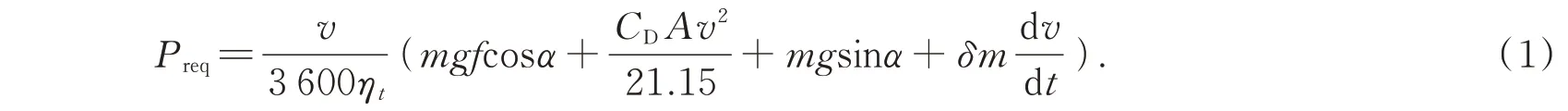
式中，Preq为需求功率，m为整车的质量，g为重力加速度，α为路面的坡度，f是滚动阻力系数，CD为空气阻力系数，A为车辆迎风面积，v为车辆需求车速，δ为质量转换系数，ηt为传动轴机械效率。

需求电功率Preq与动力电池功率Pb、超级电容功率Ps、增程器功率Pe的关系如式（2）所示，其中ηDC/DC为DC/DC 变换器的效率：

增程式电动汽车的工作模式主要分为纯电动模式和增程模式［16-17］。纯电动模式下，增程器不参与工作，由动力电池和超级电容共同工作；增程模式下，由增程器提供主要的能量来源，由超级电容承担整车驱动不足的功率或超出动力电池最大充电功率的功率。设置SSOC_b、SSOC_blow和SSOC_bhigh分别为动力电池荷电状态（State of Charge，SOC，也称剩余电量）的实际值、下限值和上限值。初始状态下，当满足SSOC_blow≤SSOC_b时，增程式电动汽车工作在纯电动模式；若SSOC_b＜SSOC_blow，则工作在增程模式，一直到动力电池SSOC_b再达到上限值SSOC_bhigh，增程器关闭，这里设置SSOC_blow=0.3，SSOC_bhigh=0.9。

2 能量管理策略分析

设计良好的控制策略能提升电动汽车的节能减排效率，本文引进了超级电容，所以增程式电动汽车主要有三个动力来源，如何实现三个动力源之间的功率分配显得尤为重要。模糊控制策略是一种与人类思维很相似的策略，相对于逻辑门限控制具有鲁棒性较强、实施简单的优点。模糊控制主要分为模糊化、模糊推理、解模糊等过程。本文设计了双模糊控制器来进行能量分配，通过判别需求功率的正负来选取不同的模糊控制器。

2.1 纯电动模式

2.1.1 驱动状态

在纯电动模式驱动状态，整车的能量来源只有动力电池和超级电容，超级电容负责承担超出动力电池平均功率部分的能量。而在逻辑门限控制当中，动力电池所能提供的平均功率值为一定值，但实际的平均功率大小受需求功率和超级电容的SOC 影响，所以本文采用模糊控制来得到不同状态下的动力电池平均功率系数Kbat0，让平均功率Pbat0在一定范围内变化。

正模糊控制器的输入为需求功率Preq，将其作论域变换后，对应的论域为（0，1），模糊集合为｛ZE，PS，PM，PB｝，分别代表｛正极低，正低，正中，正大｝；输入超级电容SSOC_s，论域为（0，1），模糊集合为｛L，M，H｝，分别代表｛低，中，高｝；输出为动力电池平均功率系数Kbat0，论域为（0，1），模糊集合为｛EL，ML，L，M，H，MH，EH｝，分别代表｛非常低，较低，低，中，高，较高，非常高｝。具体的模糊控制规则如图2（d）、表1 所示，输入与输出的隶属度函数如图2 的（a）、（b）、（c）所示，模糊规则即根据输入的信息，对应模糊规则就可以得到输出信息；隶属度函数的图像中，横坐标表示论域，纵坐标表示隶属度。

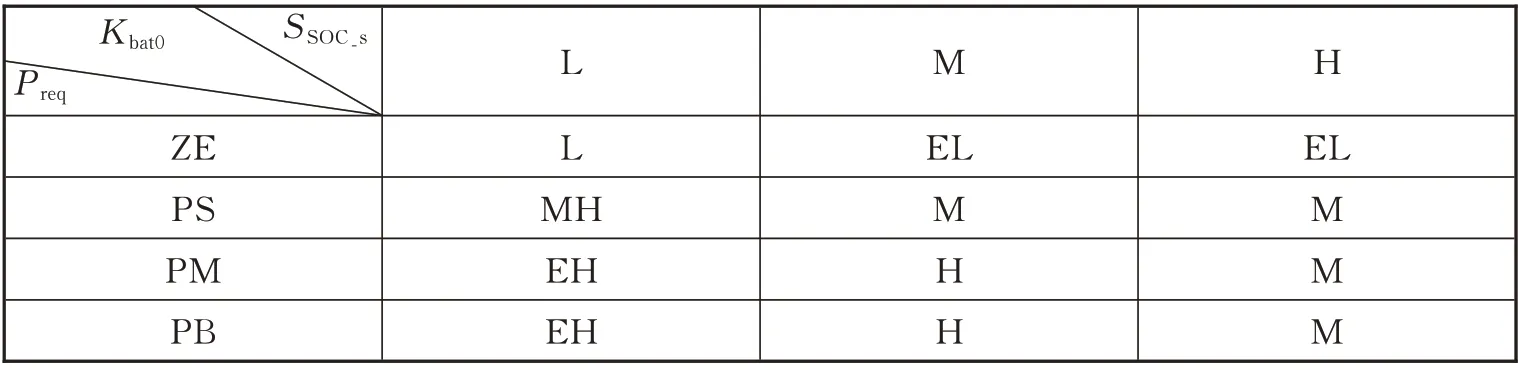
表1 平均功率系数模糊控制规则Tab.1 Average power coefficient fuzzy control rules

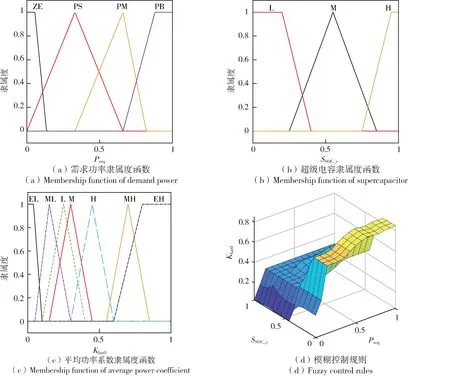
图2 正模糊控制器隶属度函数、控制规则Fig.2 Membership function and control rules of positive fuzzy controller

得到Kbat0后，可以计算出Pbat0：

得到Pbat0后比较Preq与Pbat0的大小，进一步得到Pb和Ps的大小：

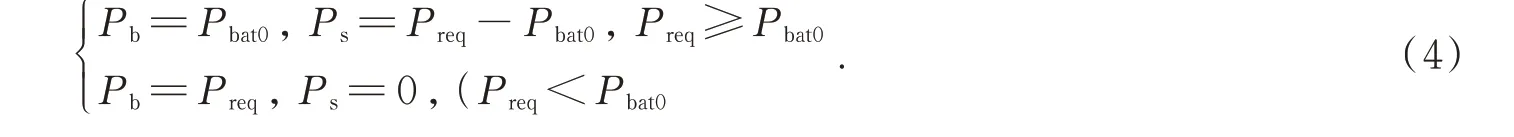
2.1.2 制动状态

制动状态下，超级电容和动力电池均可以回收能量，传统的逻辑门限控制采用两者SOC 的实际值来选择谁吸收制动能量，这样会降低回收制动的效率，本文采取功率分配模糊控制来进行制动能量的分配，负模糊控制器的输入为需求功率Preq，模糊集合为｛NB，NM，NS，ZE｝，分别代表｛负大，负中，负低，负极低｝；动力电池SSOC_b、超级电容SSOC_s，模糊集合为｛L，M，H｝，分别代表｛低，中，高｝；输出为功率分配因子Kp，模糊集合为｛LE，L，M，H，HE｝，分别代表｛极低，低，中，高，极高｝。控制规则如表2 所示。

表2 功率分配模糊控制规则Tab.2 Power distribution fuzzy control rules

得到功率分配因子Kp之后，就可以得到Pb和Ps的大小：

纯电动模式下的控制逻辑如图3 所示。

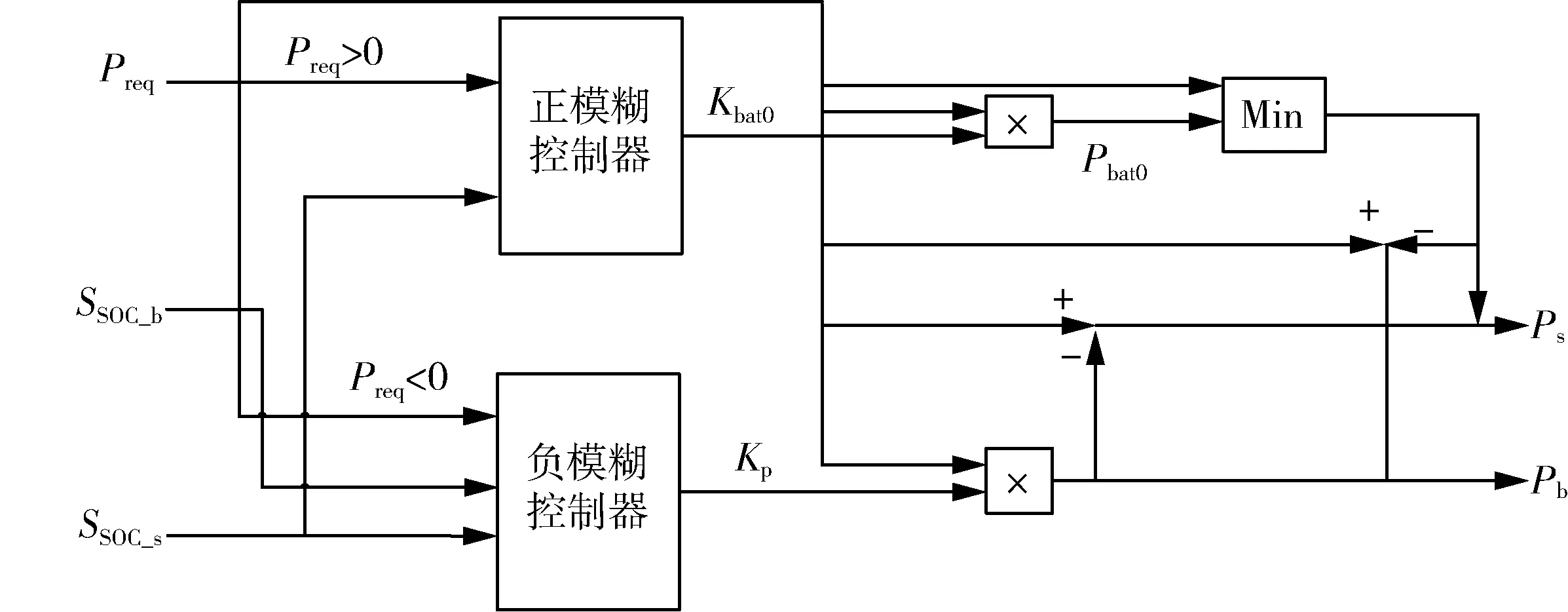
图3 纯电动模式控制流程Fig.3 Control flow of pure electric mode

2.2 增程模式

本文主要考虑电池寿命问题，所以增程模式采用发动机单点控制策略，发动机一直工作在最佳燃油消耗的工作点上，发出的功率固定，在此基础上由超级电容优先提供不足的驱动功率以及吸收过充的功率。增程模式下的控制逻辑如图4 所示。

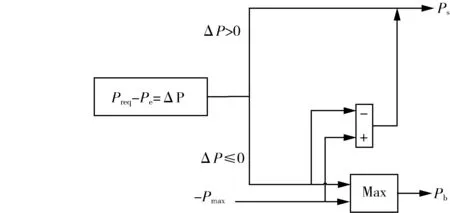
图4 增程模式控制流程Fig.4 Control flow of extended range mode

3 粒子群优化

上文的模糊控制器具有很强的主观性，在复杂的增程式电动汽车能量管理策略中很难达到最优的性能。粒子群算法最早源于对鸟类觅食行为的研究，现在适用于求解优化问题，具有操作简单，收敛速度快的特点。在粒子群算法当中，种群的任意D维粒子都代表一种潜在解，每一粒子通过跟踪个体极值Pbest以及群体极值Gbest来更新自己的速度Vd和位置Xd，具体公式如（6）所示：

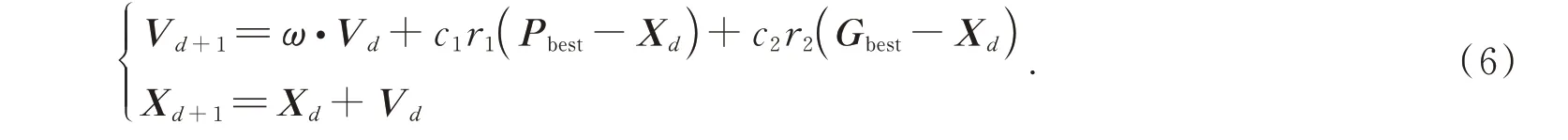
式中，ω为惯性权重，用来表示速度影响的比例；c1、c2为学习因子；r1、r2为范围［0，1］内的随机数；下标d表示粒子的id。

本文的控制策略设计原则是在满足车辆动力性能的要求下，减少动力电池的能量损耗以及增程器的燃油损耗，所以采用归一化的方法，将动力电池能量损耗EC以及增程器燃油消耗FC之和作为适应度函数，优化目标是使得适应度函数最小，适应度函数如式（7）所示。

则优化问题可以描述为式（8）：

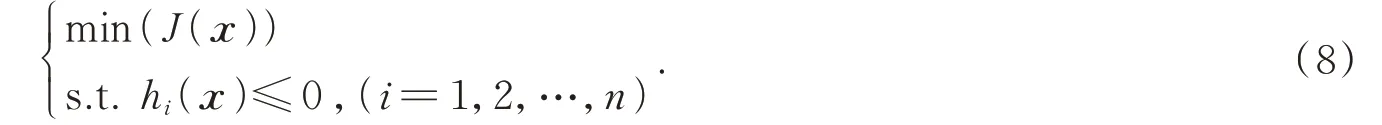
式中，函数hi(x)代表系统约束，包括车辆最高车速、爬坡性能等；x代表的是解向量，也就是待优化参数。综合考虑计算时间和优化效果，本文对隶属度函数进行优化，选取正模糊控制器的14 个隶属度函数的中心位置x1～x14，以及22 个隶属度函数宽度x15～x36作为优化参数，优化参数的变化范围如表3 所示，待优化参数x见式（9）所示，变量的范围如表3 所示，粒子群优化的主要流程如图5 所示。

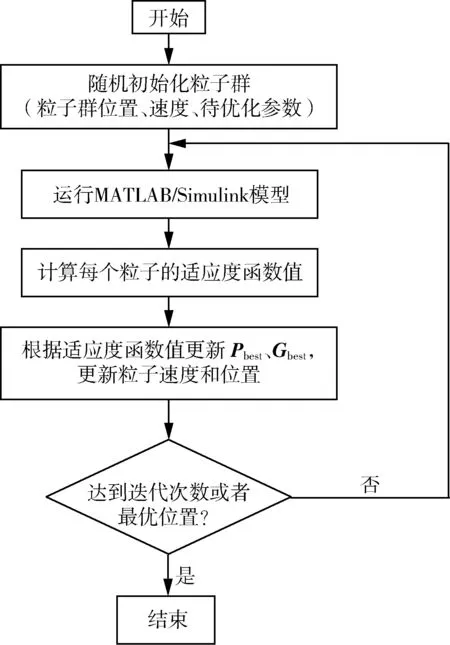
图5 粒子群优化流程Fig.5 Particle swarm optimization process

表3 待优化变量范围Tab.3 Range of variables to be optimized

4 仿真验证

为验证本文控制策略的有效性，在MATLAB/Simulink 平台下搭建了整车的仿真模型，为保证策略对比的有效性，整车各个参数保持一致。新标欧洲循环（New European Driving Cycle，NEDC）测试工况是具有代表性的乘用车行驶工况，本文选取的循环工况为NEDC，车速跟随曲线如图6 所示。由图6 可知，双模糊控制的实际车速能够跟随车辆的期望速度，说明双模糊控制能够满足整车的动力性能需求。

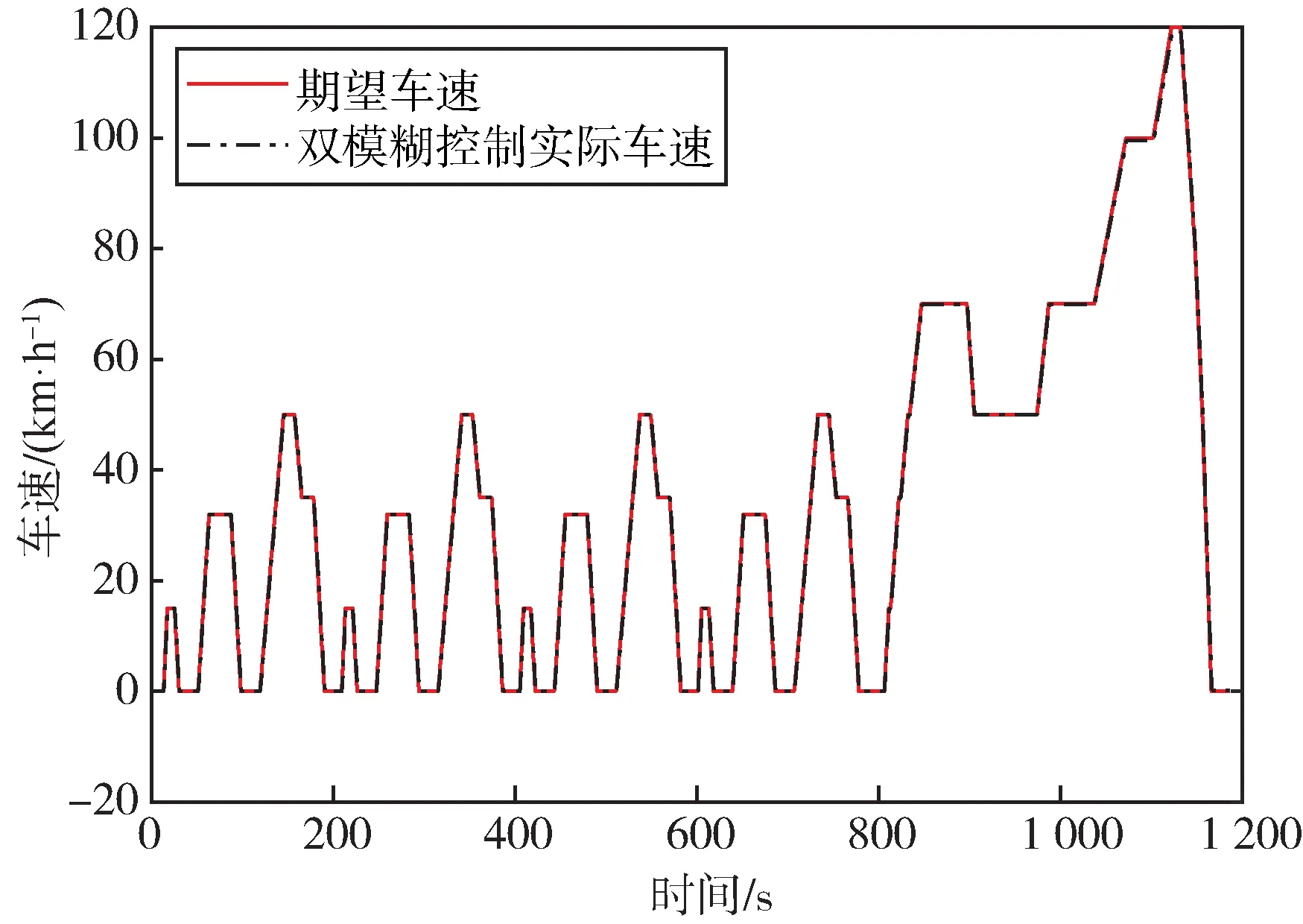
图6 车速跟随曲线Fig.6 Speed following curve

4.1 纯电动模式

在NEDC 工况下进行PSO 算法优化得到的隶属度函数如图7 所示。

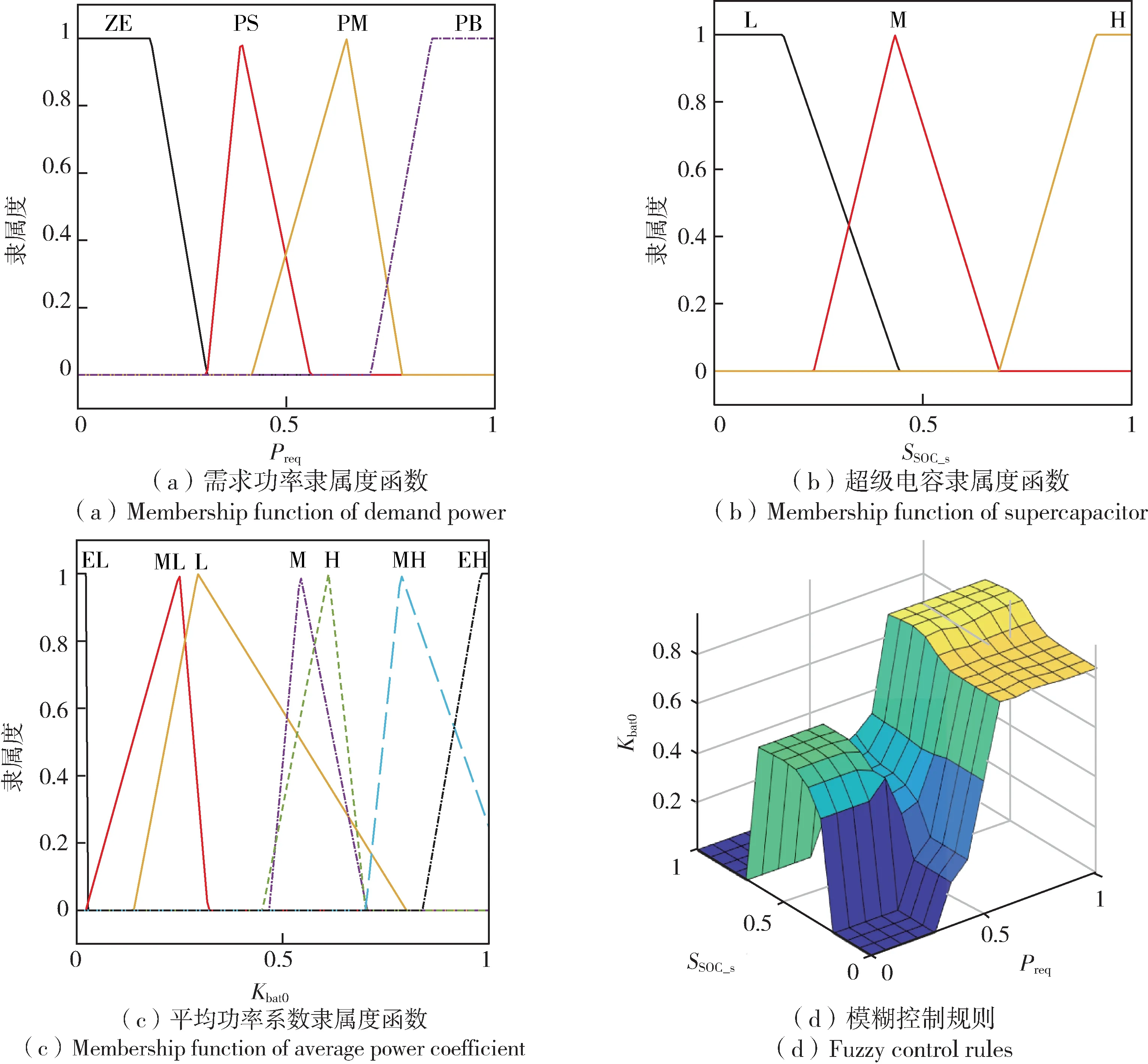
图7 PSO 优化后的模糊控制器隶属度函数、控制规则Fig.7 Membership function and control rules of fuzzy controller after PSO optimization

得到优化后的隶属度函数之后，将优化后的模糊控制器嵌入到Simulink 仿真平台的控制策略模块，并在NEDC 工况下进行仿真，得到优化后的仿真结果。纯电动模式下各控制策略的动力电池SSOC_b随时间的变化情况如图8 所示。

由图8 可知引入超级电容后，动力电池SSOC_b的终值均有所提高，PSO 优化的双模糊控制SSOC_b终值最高。相比于单电源控制的SSOC_b终值为0.744，双模糊控制的SSOC_b终值提高了11.56%，PSO 优化后的SOC终值提高了14.65%。

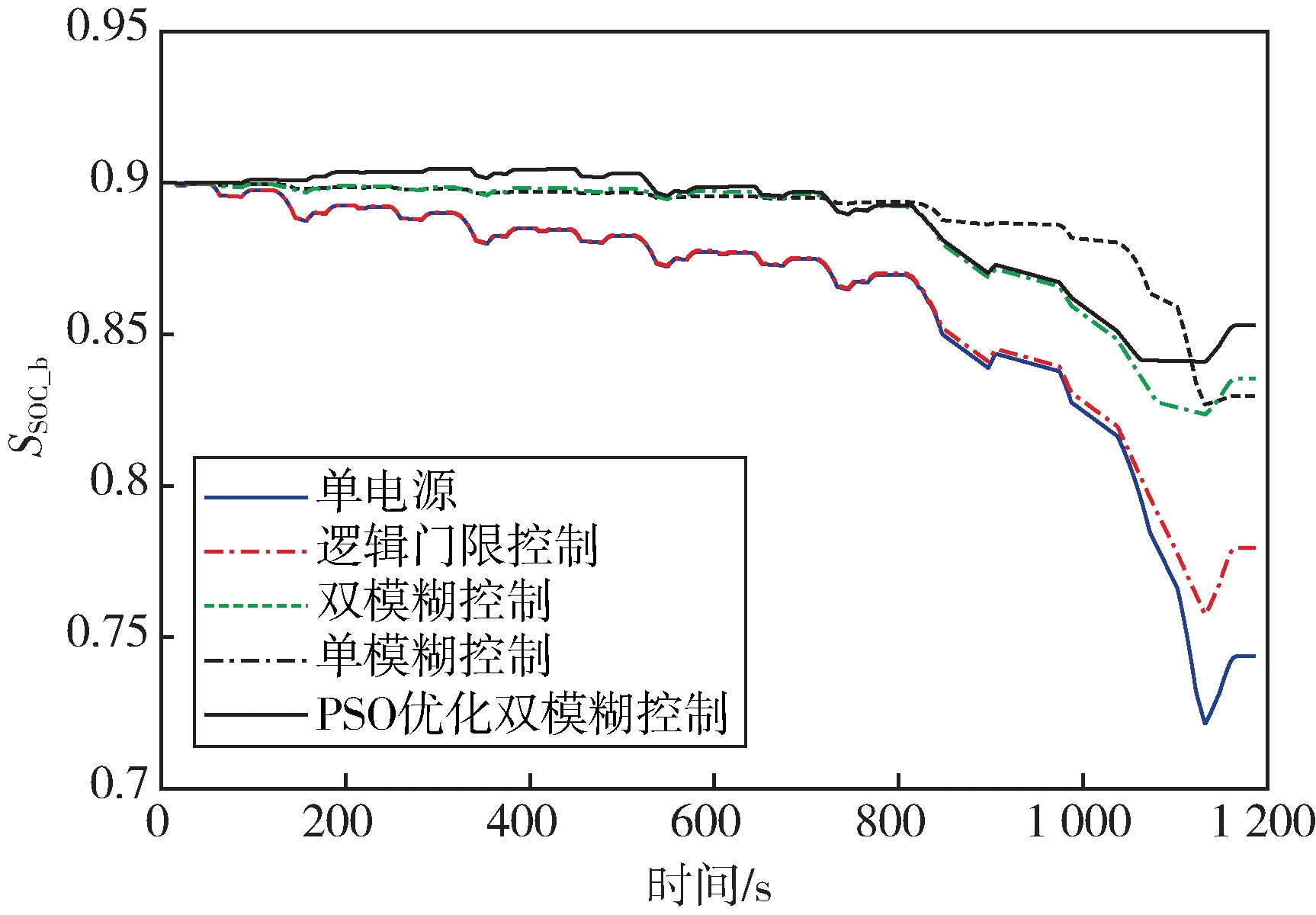
图8 动力电池SOCFig.8 SOC of power battery

充放电倍率大于1C时被认为是高倍率充放电，动力电池长期处于高倍率充放电会损伤电池的寿命，本文选取的动力电池容量为25 A ⋅h，所以充放电电流大于25 A 被认为是高倍率充放电。各策略下动力电池电流值如图9 所示，最大放电电流、平均放电电流、高倍率放电时长如表4 所示。

由图9 和表4 可知，加入超级电容后，动力电池放电电流波动减小，最大充放电电流显著减小。PSO 优化后的双模糊控制相比于未优化的双模糊控制，最大放电电流降低了20.69%，平均放电电流降低了17.78%，高倍率充放电时长有所降低；PSO 优化后的双模糊控制相比于单模糊控制，最大放电电流降低了73.71%，平均放电电流有所升高，但是动力电池电流波动较小；引入模糊控制后，高倍率充放电的时长显著减小。

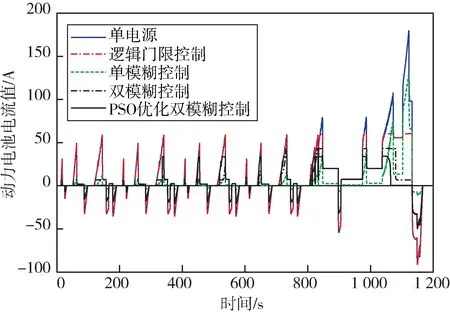
图9 动力电池电流Fig.9 Power battery current

表4 纯电动模式动力电池电流Tab.4 Electric mode power battery current

纯电动模式下逻辑门限控制、双模糊控制的SSOC_s及电流值如图10 和图11 所示。图10 中，模糊控制比逻辑门限控制的SSOC_s的变化幅度大，变化频率高；从图11 的放电电流来看，PSO 优化后的双模糊控制下超级电容承受的电流多于其他几种控制策略，超级电容起到了良好的“削峰填谷”作用，并得到了充分利用。

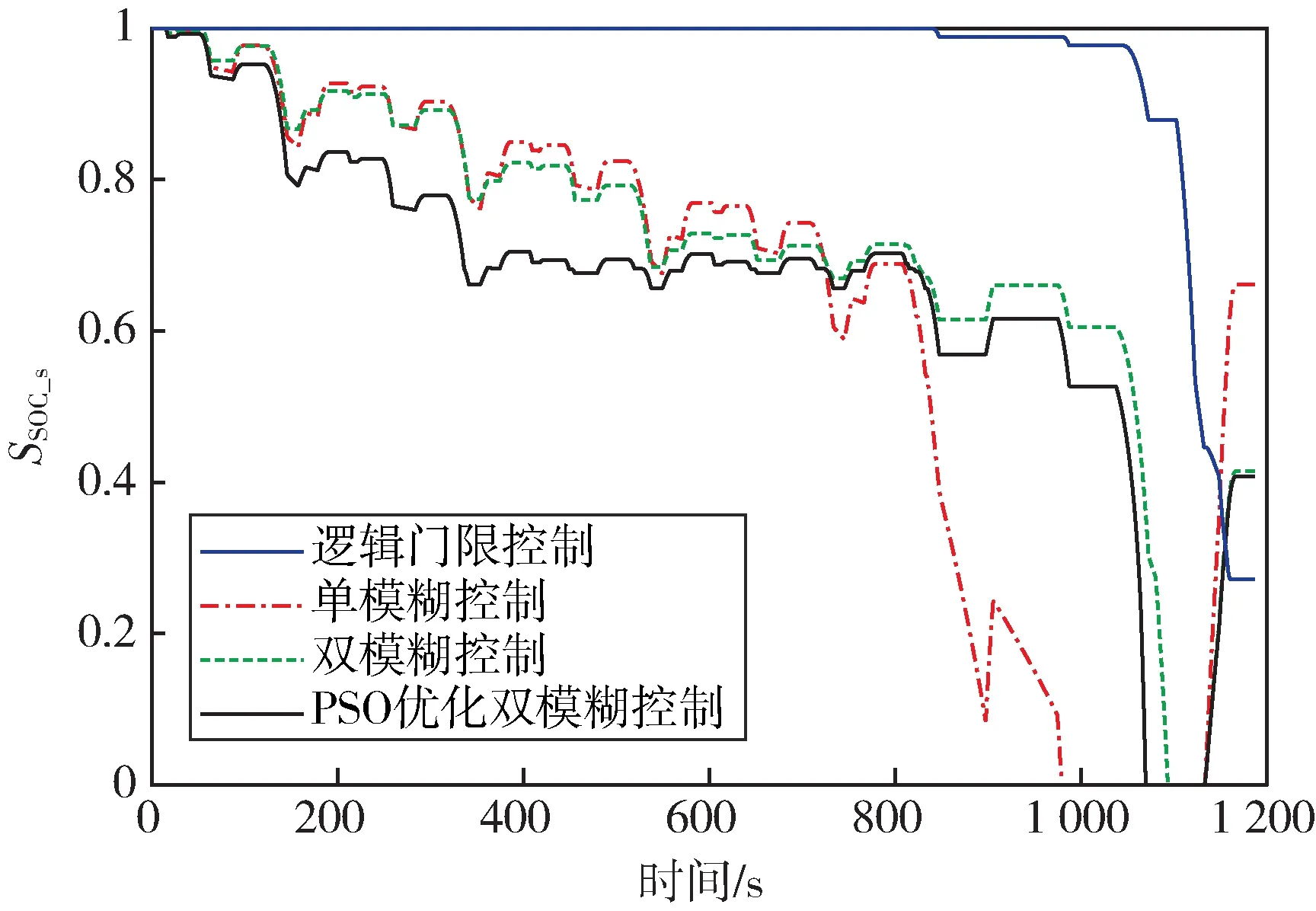
图10 超级电容SOCFig.10 SOC of supercapacitor

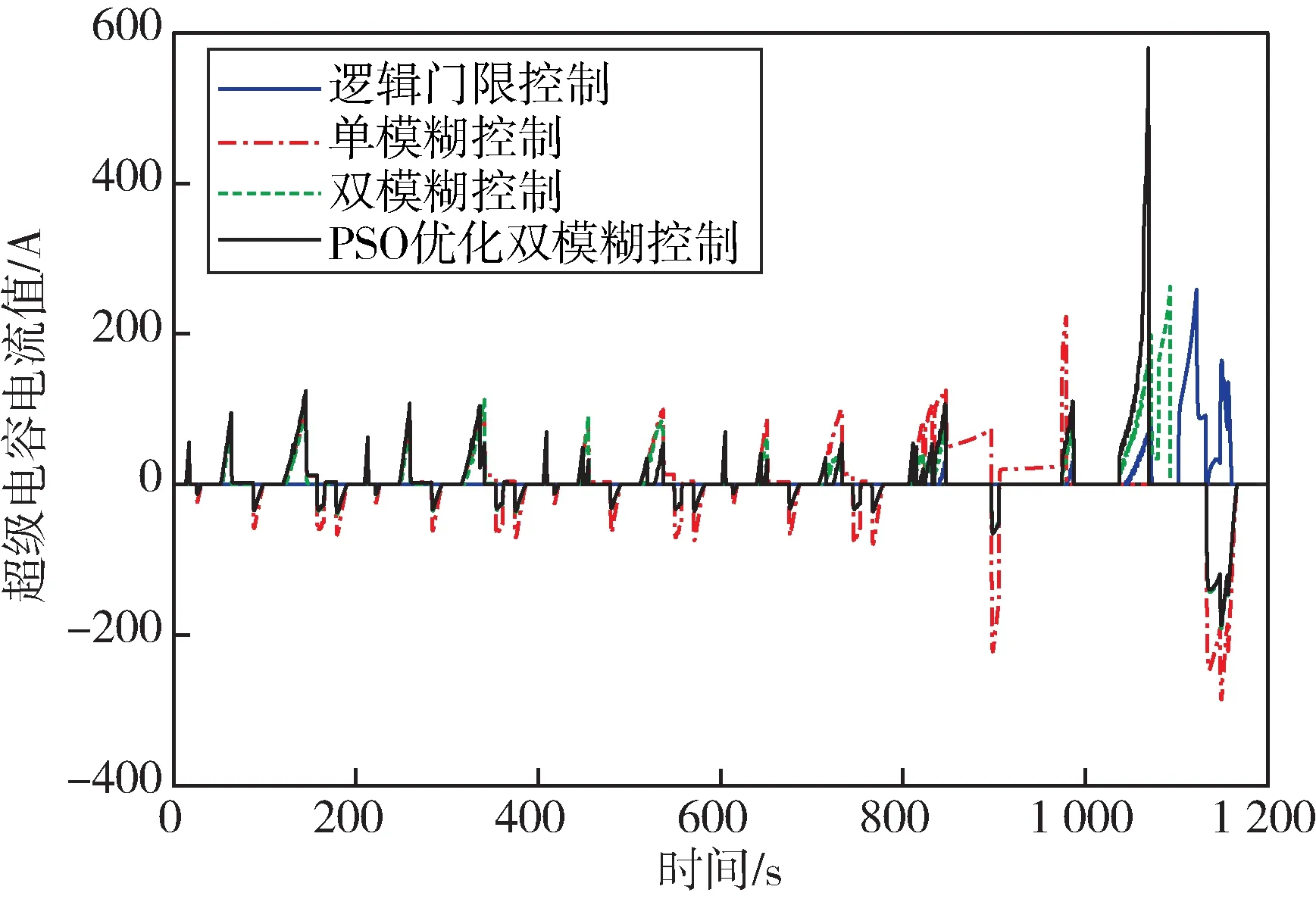
图11 超级电容电流值Fig.11 Current value of supercapacitor

4.2 增程模式

增程模式下均采用单点控制策略，所以给出单电源和PSO 优化控制策略下的动力电池SOC 值及电流值如图12 和图13 所示，单电源和PSO 优化的双模糊控制策略下，最大充电电流、平均充电电流、高倍率充电时长如表5 所示。

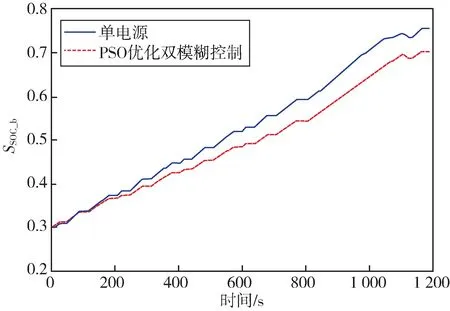
图12 动力电池SOC 值Fig.12 SOC value of power battery

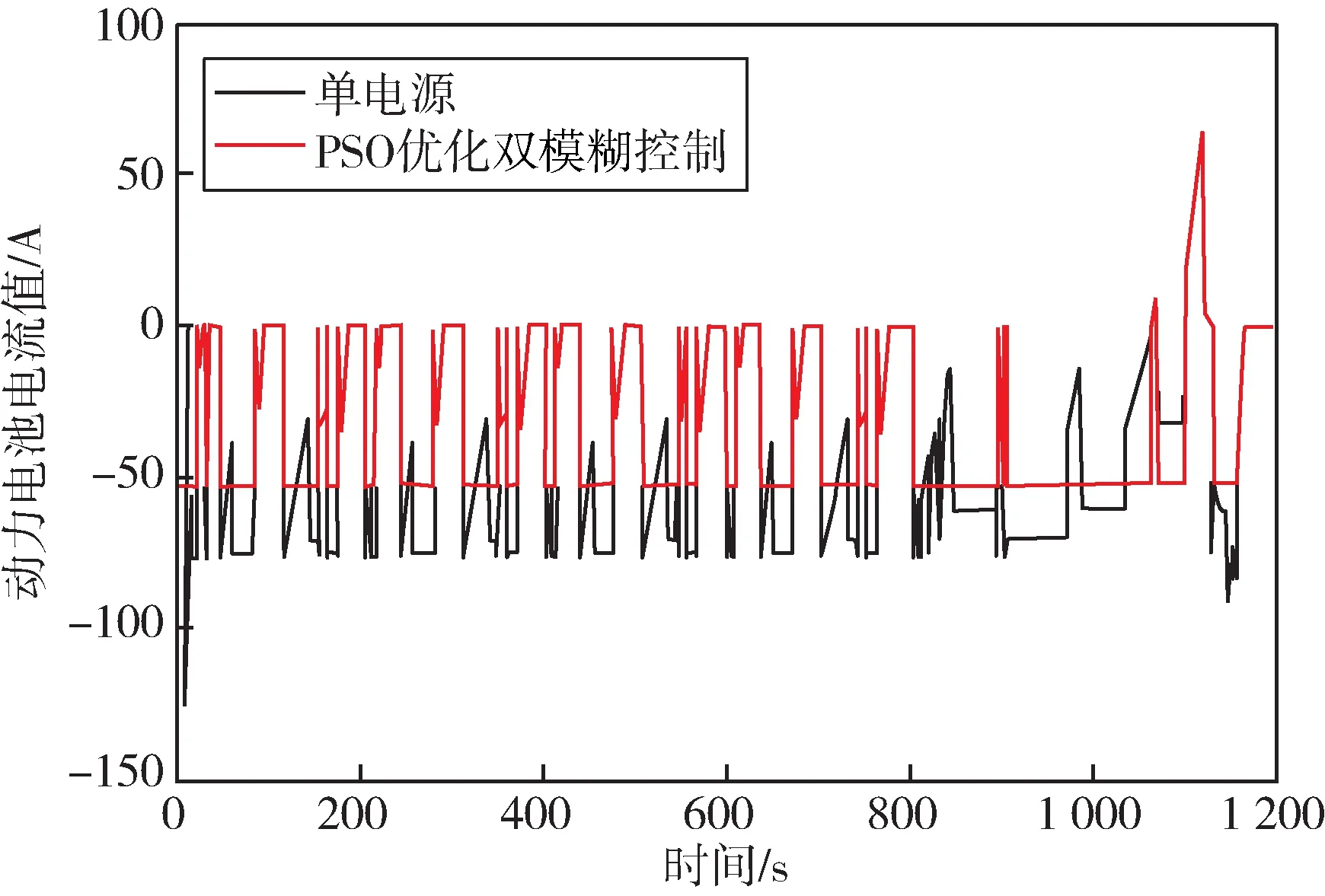
图13 动力电池电流值Fig.13 Current value of power battery

表5 增程模式动力电池电流Tab.5 Extended range mode power battery current

由图13 可知，增程模式下，单电源时动力电池的充电电流值明显大于引入超级电容后的充电电流值，这就导致了图12 的结果。但是由表5 可得，采用PSO 优化双模糊控制策略并引入超级电容后，增程模式下的最大充电电流减小了58.04%，平均充电电流减小了12.22%，高倍率充电时长也有所减小。

5 结论

通过MATLAB/Simulink 搭建顶层能量控制平台，对各种策略进行仿真，将得到的结果进行对比，得到如下结论：

（1）纯电动模式下，引入超级电容之后，各个策略的动力电池SOC 的终值（SSOC_b）均比单电源下的要高，双模糊控制的SOC 终值提高了11.52%，PSO 优化的双模糊控制的SOC 终值提高了14.65%。

（2）模糊控制策略相比于逻辑门限控制策略，超级电容的最大充放电电流均有所提高，其中PSO 优化的双模糊控制效果最好，起到了显著的“削峰填谷”的作用，超级电容得到了充分利用。

（3）PSO 优化后的双模糊控制相比于未优化的双模糊控制，动力电池放电电流波动减小，最大充放电电流显著减小，高倍率充放电时长减小，纯电动模式下，动力电池最大放电电流降低了20.69%，平均放电电流降低了17.78%。相比于单电源模式，PSO 优化的双模糊控制策略在增程模式下，动力电池最大充电电流减小了58.04%，平均充电电流减小了12.22%。这均有利于保护动力电池寿命，提升动力性能。