基于数据分布一致性的处理器硬件性能计数器复用估计方法
林新华 王 杰 王一超 左思成
(上海交通大学高性能计算中心 上海 200240)
处理器硬件性能计数器(processor hardware performance counters)是一组专用寄存器.在代码执行期间,这些计数器会记录相关处理器硬件事件(processor hardware events)的发生次数.在高性能计算(high performance computing, HPC)领域,硬件性能计数器被广泛用于性能监测与分析工具,譬如PAPI[1],HPCTOOLKIT[2],Intel VTune[3].使用者通过统计硬件事件发生次数,生成各种性能指标,分析程序在处理器上遇到的性能瓶颈[4-6].
当前主流处理器虽然能支持几百种不同硬件事件,但受限于硬件性能计数器数量(通常6~12个),同一时刻能记录的硬件事件极为有限.但在实践中,程序开发者往往需要同时监测尽可能多的硬件事件,才能更好地对程序性能进行分析与建模[7-8].为缓解这一矛盾,硬件性能计数器复用技术(multiplexing, MPX)通过分时复用策略,估计未记录的事件,从而实现利用少量硬件性能计数器记录大量硬件事件.
MPX的核心是对未记录事件进行估计的算法.已有MPX估计算法[9-12]都是基于时间局部性假设:在2个相邻被记录下的数据之间,未被记录的数据与前后数据存在紧耦合关系.此类算法利用不同插值函数,拟合未被记录的事件次数.然而,硬件事件的发生过程是一个与处理器微架构以及应用程序密切相关的复杂过程[10,13-14],因此不存在某种特定插值方法可以适用所有场景.这导致基于时间局部性假设的估计算法存在不同程度的准确率低下的问题.另外,硬件事件发生次数并不适用于某个特定的随机过程.因此如何从硬件事件发生的随机分布角度出发,设计出更加普适的估计算法是当前MPX研究的最重要挑战之一.
为应对估计精度不高的挑战,我们提出一种基于数据分布一致性的估计算法:轮廓线估计法(outline estimation, OLE).具体地,本文贡献有3个方面:
1) 通过柯尔莫戈洛夫-斯米诺夫正态性检验(Kolmogorov-Smirnov, KS)[15],我们发现针对同一硬件事件,同一代码在单计数器记录单事件(one counter one event, OCOE)模式与MPX模式下,存在数据分布一致性规律;
2) 基于此规律,我们提出轮廓线估计法OLE,通过逆向累积分布实现估计插值;
3) 我们在开源MPX库NeoMPX[16]中实现OLE,并在主流X86和ARM处理器上进行验证.实验结果表明,在对16个硬件事件同时进行记录时,OLE算法相比PAPI默认的MPX估计算法[9],结果准确率平均提高了10.5%左右,最多可提升46.6%;相比DIRA/TAM算法[10-11]和DCAM/CAM算法[12],结果准确率分别提升了18.8%和17.7%.
1 相关工作
目前已有的MPX估计算法主要有4种:
1) PAPI[1]默认使用的MPX估计算法是由May[9]提出的固定值插值算法.该算法利用前一个记录下的数据值作为固定值,插入到2次记录的数据之间.该算法是第1个基于时间局部性假设的MPX估计算法.
2) Mathur等人[10-11]量化了由MPX引起的误差,并提出了4种新的插值估计算法,其中梯形面积法(trapezoid-area method, TAM)和分隔矩形面积法(divided-interval rectangular area, DIRA)不需要预先计算,引入额外开销最低,相比May[9]的算法,结果准确度最高能提升32%左右.
3) Mytkowicz等人[13]率先提出动态时间规整(dynamic time warping, DTW)算法,对MPX生成的硬件事件时间序列进行分析.Lü等人[17]借鉴DTW算法,发现MPX事件序列中异常值是导致准确度下降的主因,因此设计了一个针对结果后处理的数据清洗器,用来消除异常值,并填充缺失值.
4) Wang等人[12]进一步阐明了Lü等人[17]未解释清楚的异常值原因,并基于Mathur等人[10-11]的工作,提出了2种新的MPX估计算法:曲面面积法(curved-area method, CAM)和分隔曲面面积法(divided curved-area method, DCAM).
上述4种估计算法都基于时间局部性假设.该假设认为在时间相邻的事件之间存在数据相关性,即临近计数值存在某种函数关系.然而,通过观察连续时间内不同时间片的硬件事件数值,我们发现相邻时间片间的记录值并没有遵循某种规律.反而,同一个程序运行时的不同硬件事件在数据分布上存在一致性规律.因此我们提出了基于数据分布一致性规律的估计算法,该算法相比基于时间局部性假设的算法更能贴近硬件事件发生的真实情况.
2 研究背景与研究动机
2.1 处理器硬件事件的记录模式
处理器硬件事件是对应用程序进行性能分析与建模的重要指标,譬如每周期执行的指令数(instr-uction per cycle, IPC)、浮点运算执行的指令数、缓存访问失效率等.这些重要指标可以反映应用程序运行时,处理器微架构层次上不同模块的实际性能,例如IPC对应处理器的指令吞吐量;缓存访问失效率对应程序的数据局部性.
本文选取PAPI[18]作为研究平台,这是HPC领域最具影响力的开源性能分析工具之一.PAPI提供2种记录硬件事件的模式:单个计数器记录单个事件的OCOE模式与多个计数器同时记录多个事件的MPX模式.
OCOE模式是指每个硬件计数器在程序运行期间只针对一个硬件事件进行计数.OCOE模式的优势是计数结果准确,因此本文将OCOE 模式的计数结果作为评估结果准确率的基准;OCOE模式的局限是每次能记录的事件数量受限于硬件计数器的数量,例如Intel Cascade Lake处理器可用计数器仅为8个.在OCOE模式下,要记录48个硬件事件需重复运行6次程序,每次运行记录8个不同事件.
2.2 MPX模式的原理
MPX模式采用分时复用[9]的方法,将各个硬件计数器的可用时间切分成不同的时间片,然后在不同的时间片上轮流记录不同的硬件事件.在MPX模式下,硬件性能计数器在多事件调度过程中,存在部分事件发生次数未被计数器记录的情况.此时估计算法将估算该时间段内硬件事件的发生次数,补全未被记录的数据.
因此,MPX主要有2个步骤组成:
1) 时间片调度.由于MPX模式基于分时复用,不同的硬件事件会轮流在硬件计数器上记录,其调度需要通过操作系统的内部计时器和信号处理功能实现.
2) 算法估计.由于时间片调度过程中部分硬件事件未被记录,因此需要使用估计算法通过已记录的事件数据,估算出未被记录的事件数据.目前已有算法都是使用插值法对该事件未被记录的时间片进行估算填充.以PAPI默认的MPX估计算法[9]为例,该算法使用最近一次记录的事件数值进行插值填充,以补全未记录事件数的时间片.如图1所示,在事件A未被调度的时间片内,若事件A的实际发生率小于默认算法的估计值,则事件A的估计值会明显高于实际值;反之,若事件A的实际发生率大于默认算法的估计值,则事件A的估计值会明显低于实际值.对于上述2种情况,PAPI默认的MPX估计算法无法进行调整,因此会引入误差较大的异常值.这正是MPX异常值的主要来源之一[12,17].
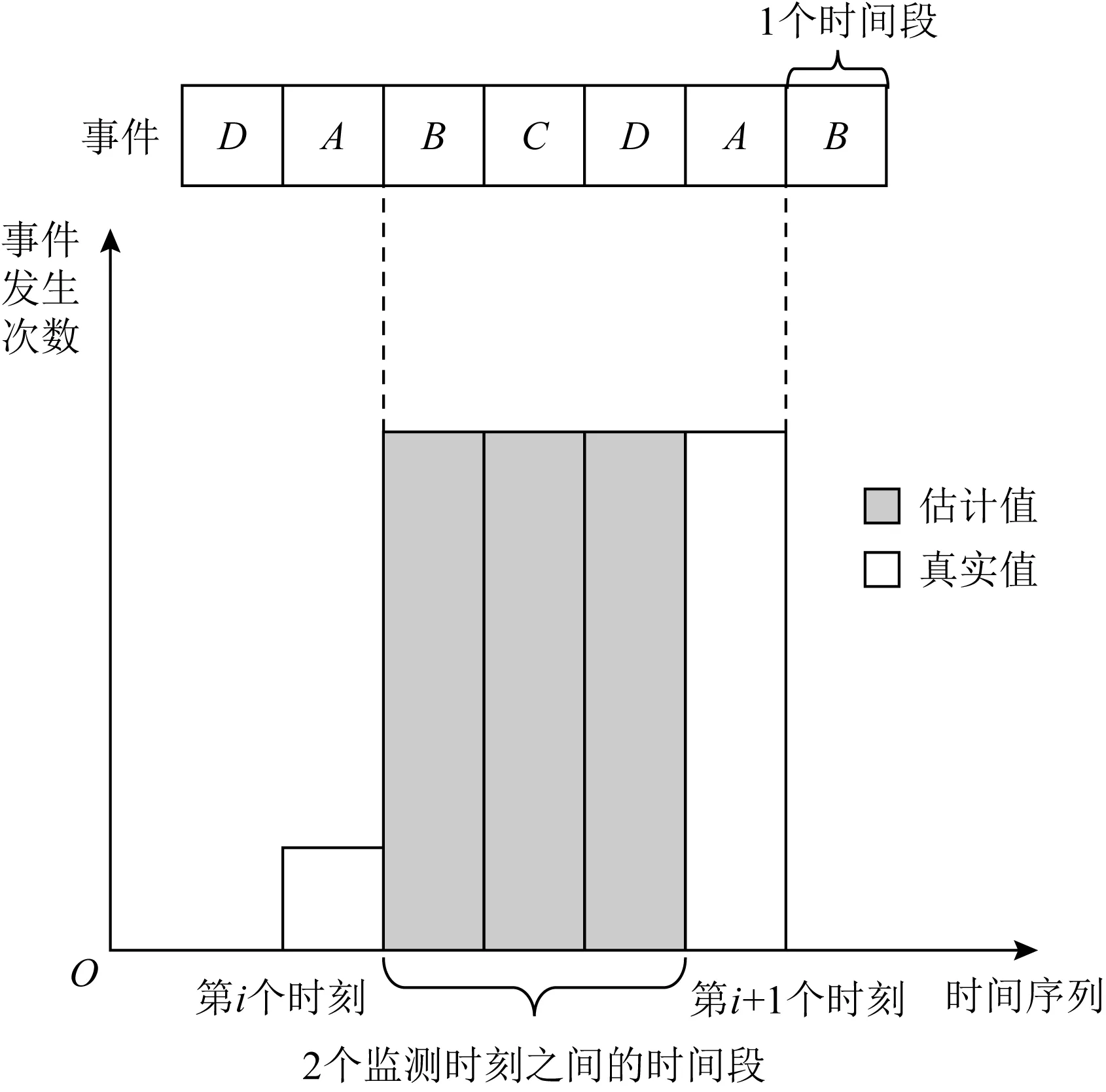
Fig. 1 Default MPX estimation algorithm in PAPI[9]图1 PAPI默认的MPX估计算法[9]
2.3 基于时间局部性假设的MPX估计算法
已有MPX估计算法都是基于时间局部性假设.这种假设是基于代码执行的局部性原理,认为在局部的时间片上处理器运行相同代码片段时,在时间上相近的硬件事件记录值会相近或是遵循统一的变化趋势,从而导致硬件事件的相邻记录点之间存在某种数据相关性.
这种数据相关性的具体体现是相邻记录点之间存在某种函数关系.譬如PAPI默认的MPX估计算法[9]假设相邻记录点之间的计数值相同,因此就直接采用临近记录点的计数值作为预测结果来填补未记录时段的计数值.但这种等值预测的估计方式误差较大,因此Mathur等人[10-11]提出了基于线性增长方式的算法,而Wang等人[12]则进一步提出了基于指数增长方式的CAM和DCAM算法.如图2所示,DCAM算法对于2个记录点之间的硬件事件发生次数,以曲线函数中常用的指数函数进行递增插值.与线性增长插值算法[10-11]相比,DCAM更符合硬件事件发生时的非线性规律,但仍遵循单一变化率趋势进行插值,具有一定的局限性[12].
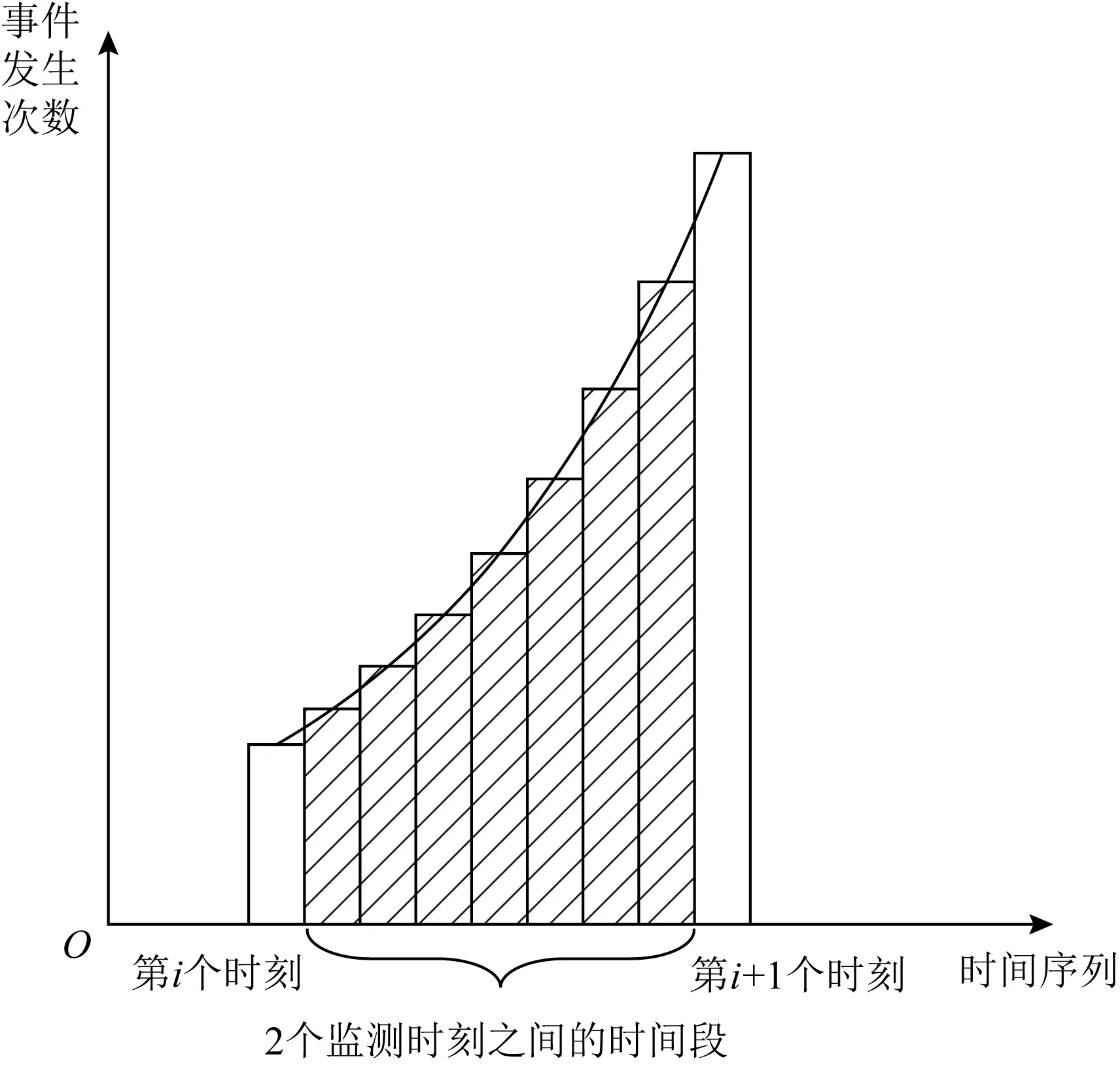
Fig. 2 DCAM estimation algorithm[12]图2 DCAM估计算法[12]
3 MPX估计算法设计
我们首先对MPX模式下硬件事件的数据分布进行分析,然后受KS检验[15]启发提出基于数据分布一致性的MPX估计算法.
算法相关变量的定义:
Δcountraw=MPX和OCOE采集数据之间的差值;
Tend=程序运行总时间序列数据;
Trun=记录总时间序列数据;
Inci=2次记录数值之间的变化梯度.
3.1 MPX数据分布呈现一致性规律
通过观察连续时间内不同时间片的硬件事件记录值,我们发现相邻时间片的记录值并不遵循时间局部性假设(见2.3节).经分析,原因为:考虑硬件事件计数器的记录时延、线程调度等多种因素影响,并结合我们的测试数据,推测PAPI的计时误差应该在1 ms左右,因此将PAPI的记录时间片设置为10 ms以上才能获得较为准确的记录数据.而结合现代处理器的频率和指令集设计可知,单个时间片内可运行的指令数在百万数量级,即使换算成高级语言也很难确保局部时间片上处理器运行了相似代码片段.因此实践中,时间局部性假设不成立.
我们对MPX模式下采集到的数据与OCOE模式下采集到的数据进行KS检验,分2步:1)对数据进行预处理,将采集到的Δcountraw进行排序,得到由小到大的Δcountraw序列数据;2)通过对比2组数据之间的累计分布函数,检验数据分布一致性.我们从Rodinia基准测试集[19]的6个测试程序中,针对16个硬件事件进行KS检验,结果显示平均的D值为0.10,最小值为0.06,平均的P值为0.90,最大值为0.95.该结果表明针对同一硬件事件,相同代码在OCOE和MPX这2种模式下数据分布呈一致性.以HeartWall测试程序为例,图3为硬件事件dtlm:m在这2种模式下的累积分布图,2种模式下的数据在不同时刻的总体分布呈现高度相似.
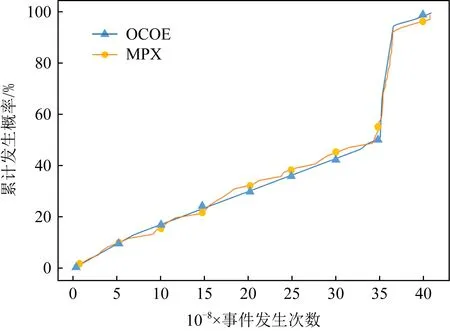
Fig. 3 Cumulative distribution of the dtlm:m event with OCOE and MPX modes in HeartWall图3 HeartWall中事件dtlm:m在OCOE和MPX 2种模式下的累积分布图
3.2 基于数据分布一致性的MPX估计算法
根据MPX数据分布呈现一致性规律,我们提出一种全新的MPX估计算法:轮廓线估计法(OLE).该算法包括数据预处理和基于轮廓线插值2个步骤.
1) 数据预处理.为保证在增加估计插入值后的序列数据与插入前的序列数据相比仍能保持分布一致性,我们对排序后的Δcountraw数据序列中的每个数据做编号处理.这些编号不是连续的,而是在2个连续序列数据的编号中空缺一定比例的编号,并且空缺的比例在整个编号序列中是均匀的.空缺的比例可由Tend和Trun计算得到.
具体来说,为每个Δcountraw序列数据设置编号的策略为:为保持增加估计计数值后的序列数据与原始序列数据分布一致,我们按照Inci=Tend/Trun对编号做了等比例的缩放.我们分别对Inci的整数部分和小数部分做累计,整数部分或小数部分每加1,则空出1个序列号以备后续作为估计计数值的编号,并将开头的编号作为当前原始序列计数值的编号.在实现中,为防止估计值整体偏大,我们对小数部分累计值采取满0.5加1、满1置0的策略.预处理步骤的完整描述如算法1所示:
算法1.数据预处理的算法.
输入:硬件事件A的程序运行总时间序列数据Tend与记录总时间序列数据Trun的比值P;
输出:原始序列计数值编号S1、估计序列计数值编号S2.
过程:SeqNum(P)
①c←0,F←0;
② forpinPdo
③c←c+1;
④S1.append(c);
⑤i←int(p);
⑥F←F+p-i;
⑦ ifF>0.5
⑧c←c+1,S2.append(c);
⑨ end if
⑩ end for
2) 基于轮廓线插值.在获得原始计数值序列及其编号序列对后,我们利用2层神经网络对序列对做拟合操作,使神经网络拟合出一个平滑的排序外轮廓线.选择2层神经网络拟合是因为根据万能近似定理,2层神经网络可以拟合任意函数.这个轮廓线上所有数据组成的数据序列的数据分布与原始序列数据的数据分布是一致的.最后将获得的估计计数值编号代入轮廓线函数中,从而获得估计计数值序列数据.基于轮廓线插值步骤的完整描述如算法2所示:
算法2.基于轮廓线插值的算法.
输入:硬件事件A的程序运行总时间序列数据、记录总时间序列数据、记录计数值C;
输出:硬件事件A在程序运行期间发生的次数Cfinal.
过程:OLE(Tend,Trun,C)
①Cfinal←0;
② ΔTend[i]←Tend[i+1]-Tend[i];
③ ΔTrun[i]←Trun[i+1]-Trun[i];
④ ΔC[i]←C[i+1]-C[i];
⑤ ΔTend_s,ΔTrun_s,ΔCs←ArgSortOnC(ΔTend,
ΔTrun,ΔC);
⑥S1,S2←SeqNum(ΔTend_s/ΔTrun_s);
⑦Cfinal←Cfinal+sum(ΔCs);
⑧N←regression(Si,ΔCs);
⑨ foriinS2do
⑩Cfinal←Cfinal+N.predict(i);
4 算法实现及调用方式
为检验OLE算法提升MPX准确率的效果,我们在开源MPX库NeoMPX[16]中实现OLE算法.NeoMPX库兼容PAPI,已集成多种MPX算法,包括TAM,DIRA,CAM,DCAM等.NeoMPX库具有良好的可扩展性,可新增其他MPX估计算法.
NeoMPX的软件架构如图4所示,整体流程分为3个主要步骤:调度、采样和估计.其中调度部分沿用PAPI的标准设计,使用Linux系统工具perf提供的接口,直接获取调度结果.为了保证时序采样的精准性,子进程专门对父进程运行的应用程序的事件进行定时采样,并在程序运行完后,基于采样序列进行估计.图4中的估计模块中(子进程),我们加入了新实现的OLE算法.
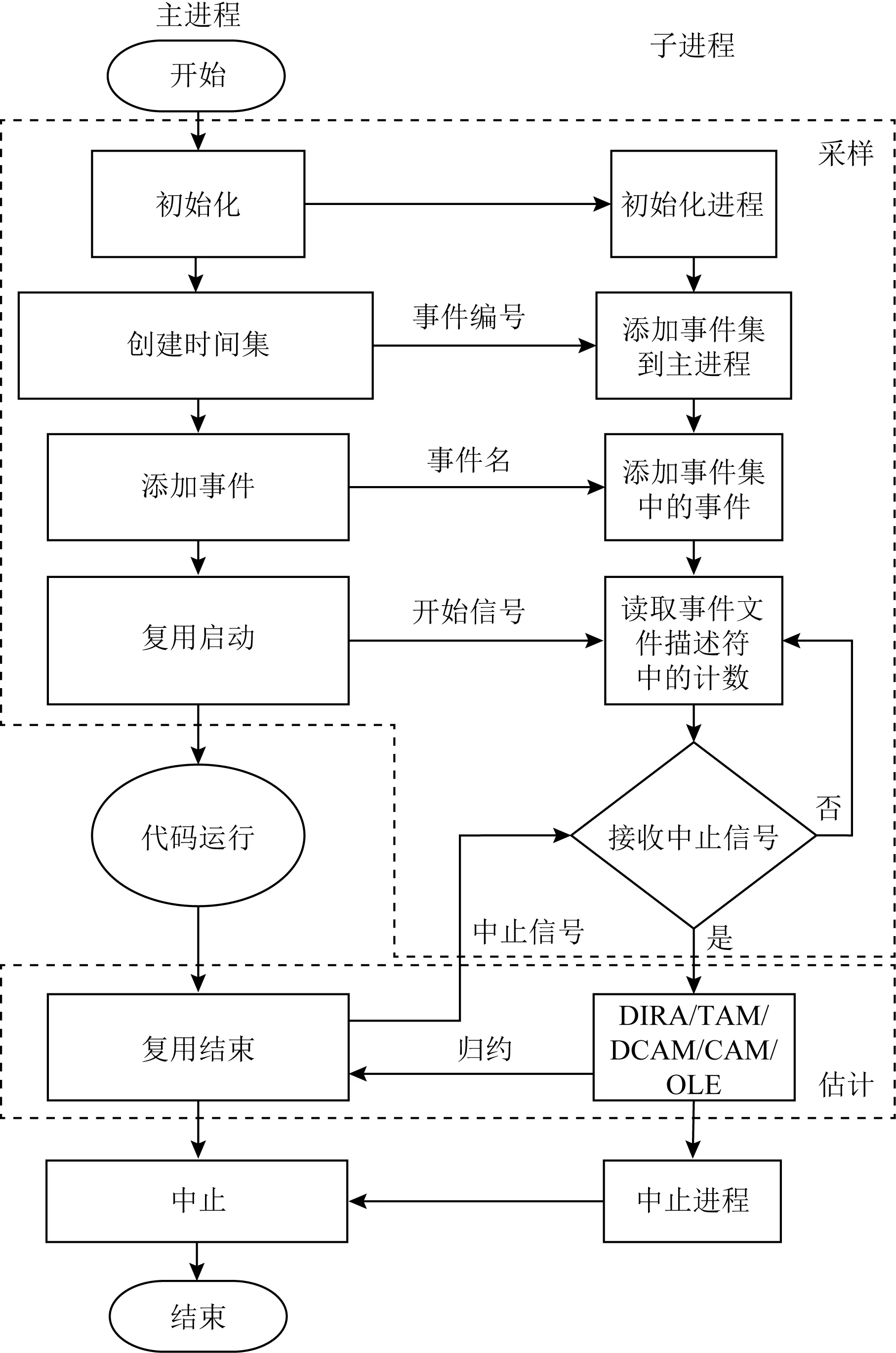
Fig. 4 The software architecture of NeoMPX图4 NeoMPX软件架构图
NeoMPX算法框架采用2层可扩展设计:上层组合不同通用算子实现不同的估计算法;下层集成不同估计算法中用到的通用算子.基于这个可扩展框架,NeoMPX不仅可以通过调用不同API来使用不同估计算法,而且在新增OLE算法时,仅需针对估计算法模块添加入新算法的实现,并用API封装即可.
NeoMPX库兼容标准的PAPI API,因此使用方式与PAPI完全一致.MPX估计算法可以通过API显式地进行选择.如图5所示,在NeoMPX库中显式调用OLE算法(行13).
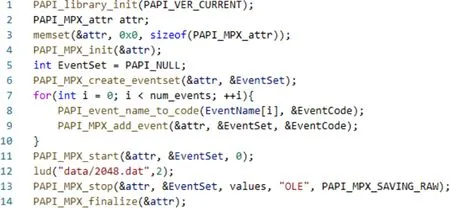
Fig. 5 The sample code of invoking OLE in NeoMPX图5 在NeoMPX库中调用OLE的示例代码
5 实验设置
1) 硬件平台.我们选取当前主流的X86和ARM的处理器作为实验平台,分别是Intel Xeon Gold 6248和Huawei Kunpeng 920.这2款处理器都是2019年发布的全新架构,与硬件事件相关的参数如表1所列.从表1中可以看出,处理器能支持的硬件事件数量远大于硬件计数器数量.操作系统使用CentOS,以保证Linux perf对多事件调度的实现一致.

Table 1 The Specification of Two Mainstream Processors About Hardware Counters表1 2款处理器与硬件事件相关的参数
2) 基准测试程序.Rodinia[19]是HPC领域国际上流行的一款测试程序集.为检验OLE算法的使用效果,我们选取Rodinia的6个典型测试程序,如表2所示.这6个测试程序涵盖HPC领域的4种不同数值计算模式以及5个不同应用领域.

Table 2 Six Evaluated Benchmarks from Rodinia表2 6个Rodinia测试程序
测试中,这些测试程序的运行参数都使用默认值,且我们在这些程序源代码中插入PAPI和NeoMPX库的API调用,如图5所示.
3) 处理器硬件事件.主流处理器能支持的硬件事件很多(可达上百个),但性能分析与建模中最常用的事件并不需要那么多,因此我们在2款测试处理器上分别选取了16个最常用的硬件事件.如表3所示,在Intel X86处理器上选取的16个硬件事件涵盖了分支预测和TLB访问等5类关键事件类型.

Table 3 Sixteen Evaluated Hardware Events on Intel CPU表3 Intel处理器上的16个常用的硬件事件
4) MPX估计算法.我们选取5个最典型的MPX估计算法与OLE算法进行对比,分别是:PAPI默认的MPX估计算法、Mathur等人[10-11]提出的TAM和DIRA算法、Wang等人[12]提出的CAM和DCAM算法.
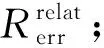
① OCOE模式的每个硬件计数器在程序运行期间内只对一个硬件事件进行计数,不存在任何估计导致的误差,因此将其作为基准结果.则MPX估计算法(相对OCOE模式)的错误率Rerr为
(1)
(2)
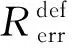
② 对不同硬件事件,在所有测试程序中的准确率提升为
(3)
6 结果分析
为全面分析实验结果,我们从测试程序、硬件事件以及跨处理器这3个不同角度进行分析.
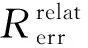

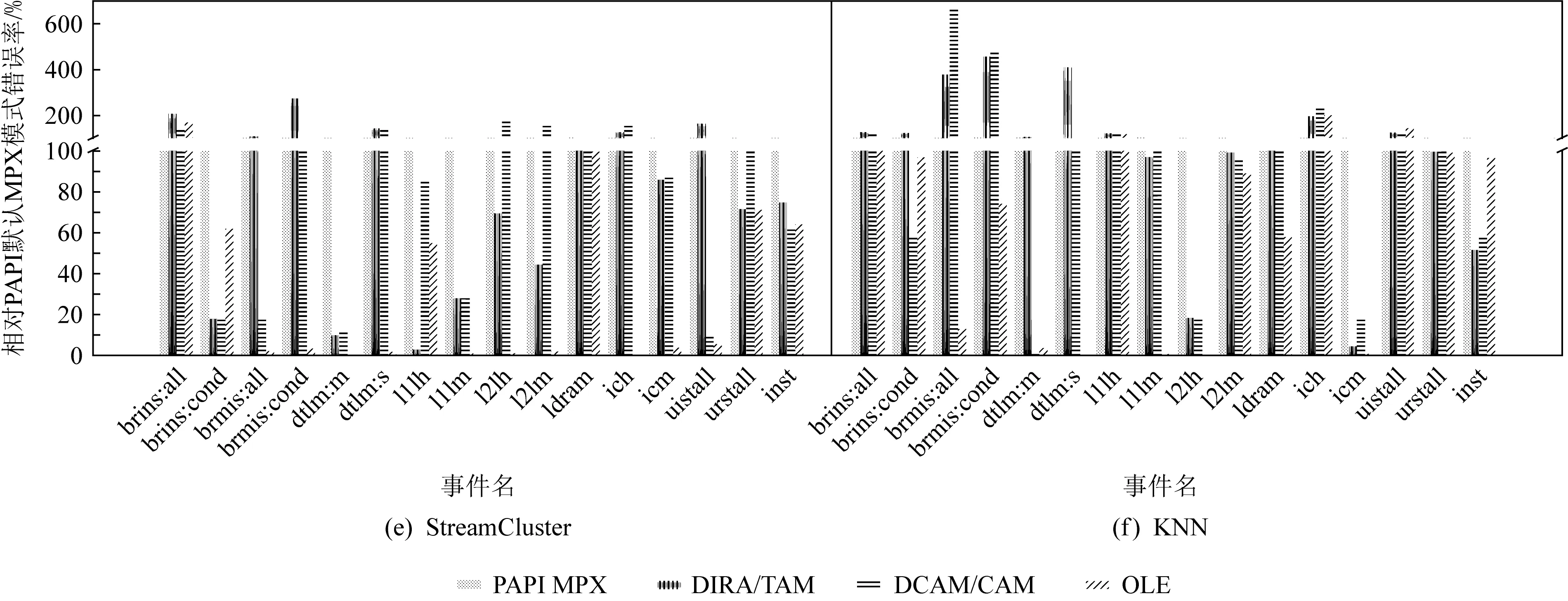
Fig. 6 The relative error ratio (to PAPI default) of the five MPX estimation algorithms图6 5种MPX估计算法相对PAPI默认MPX估计算法的错误率
进一步分析,我们发现OLE在HeartWall(结构化网格)、KNN和StreamCluster(密集线性代数)90%的硬件事件中都能有效低相对错误,这表明OLE针对结构化网格和密集线性代数算法有很好的效果.
2) 从硬件事件的角度.表4对比了5种MPX估计算法的准确率提升.我们将基于时间局部性假设的4种不同算法(DIRA,TAM,DCAM,CAM)根据算法类型分为2类,每一类都选取最优结果来比较.
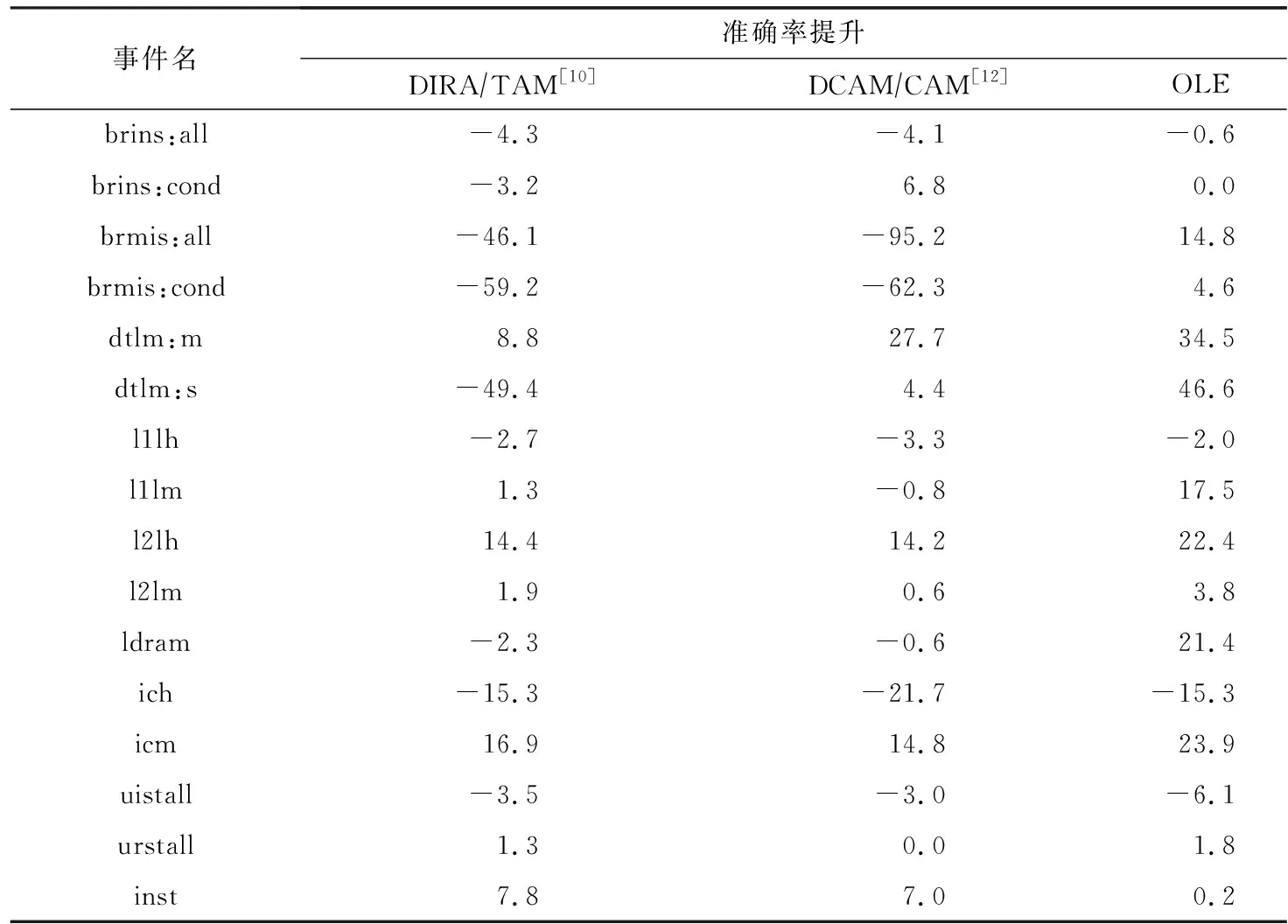
Table 4 Comparison of Accuracy Improved Ratio for Estimation Algorithms on Events表4 估计算法对事件准确率提升的对比 %
如表4所示,OLE相比PAPI默认MPX评估算法,准确率平均提升了10.5%左右,最多可提升46.6%;相比DIRA/TAM和DCAM/CAM这2类算法,准确率平均分别提升了18.8%和17.7%.
进一步分析,我们发现:
① 在最坏情况下,OLE比其他2类基于时间局部性假设的算法,都有更好的结果(参见表4,-15.3%比-59.2%和-95.2%);
② 在性能建模领域中,最常用的访存相关的硬件事件,其中有3个事件OLE都取得了约20%的准确率提升;
③ 对TLB相关的硬件事件dtlm:m和dtlm:s,OLE对结果准确率提升更具优势(34%~46%).
这些结果显示,OLE有助于MPX在性能建领域的进一步应用.
3) 从跨处理器的角度.为评估OLE算法在不同处理器之间的普适性,我们在2款主流X86和ARM 处理器上进行实验对比.表5展示了3类算法(包含DIRA,TAM,DCAM,CAM,OLE,结果均取最优值)在不同处理器上的平均准确率以及最大、最小准确率的提升.
实验结果显示,OLE在Intel处理器上获得了平均10.5%的准确率提升,在ARM处理器上获得了平均3.5%的准确率提升,均高于其他4种基于时间局部性假设的估计算法.这说明OLE在跨处理器上,能获得更稳定、更精确的计数结果.

Table 5 Comparison of Accuracy Improved Ratio for Five Different Estimation Algorithms表5 5种估计算法准确率提升对比 %
7 结 论
MPX允许处理器使用数量有限的硬件性能计数器来记录更多的硬件事件,但现有基于时间局部性假设的MPX估计算法准确率过低,导致MPX在实际场景中一直未被广泛使用.为此,本文提出了一种基于数据分布一致性的轮廓线估计法OLE,通过对硬件事件分布进行排序,逆向累积分布实现估计插值,从而有效提升MPX估计结果的准确率.
下一步,我们将结合基于时间局部性假设的工作[12]以及本文基于数据分布一致性规律的工作,设计一套自适应MPX框架,针对不同应用与处理器,根据实时采集的硬件事件的数据特征,动态选择最优的MPX估计算法.
作者贡献声明:林新华负责全文框架设计、论文撰写、全文修订、最终审核;王杰负责内容设计,提出算法和实验设计;王一超负责论文整体研究思路、部分论文撰写、最终版本修订;左思成负责文献调研和撰写、论文插图设计和修订.

