大规模脉冲星候选体信号的无监督聚类分析研究∗

刘 莹 马 智 游子毅 王 培 党世军 赵汝双 董爱军

(1贵州师范大学物理与电子科学学院 贵阳 550025)

(2中国科学院国家天文台 北京 100012)

1 引言

脉冲星领域的发现有力地推动了天文学、物理学及导航等相关领域的发展[1–2].随着500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope,FAST)的建成和19波束脉冲星漂移扫描巡天项目的开展,其高灵敏度且更大天区覆盖面的特点,在带来脉冲星信号搜寻范围的优势同时也产生了海量的观测数据,如何有效地从海量数据中筛选出脉冲星候选体成为脉冲星搜寻的关键.

基本的脉冲星搜寻中所需完成的工作为在周期(Period,P)-色散量(Dispersion Measure,DM)组成的两维空间中搜索稳定周期性脉冲信号.目前,图形工具辅助或基于统计的传统方法已无法满足如此庞大数据量处理的需要.人工智能技术运用于脉冲星的候选体筛选根据方法原理主要分为3类.第1类是基于经验公式的候选体排序算法,Lee等[3]提出的PEACE(Pulsar Evaluation Algorithm for Candidate Extraction)算法依赖于一些假设,如信噪比、脉冲轮廓形状等,在实际处理得到的脉冲星候选体中很多特征都不能很好地拟合理想的特征形状,从而可能导致一些有特殊形状脉冲,如宽脉冲、偏离色散量-信噪比(DM-S/N)曲线或者低流量的脉冲星被遗漏.第2类是直接利用候选体诊断图自动提取特征的神经网络图像识别模型.Wang等[4]提出基于FAST漂移扫描测量的神经网络群方法,标志着深度神经网络图像模式识别系统(Pulsar Image-based Classification System,PICS)的进一步发展.Zeng等[5]通过改进周期信号筛选算法(sifting)设计了一种Concat卷积神经网络(Concat Convolutional Neural Network,CCNN)来识别从FAST收集到的候选体.刘晓飞等[6–7]提出基于深层残差网络的脉冲星候选体分类,可以有效提高脉冲星候选体自动识别的精度.这类方法促使模型通过数据驱动学习,从诊断子图中自主学习“类脉冲星”的模式.相比传统机器学习方法泛化性更好,但需要手动标记每个训练数据的子图且样本训练需求量较大,导致大量额外工作量的投入.第3类是基于机器学习的分类算法,包括基于人工神经网络的SPINN(Straightforward Pulsar Identification using Neutral Networks)分类器[8]、高斯-黑林格快速决策树(Gaussian Hellinger Very Fast Decision Tree,GH-VFDT)[9–10]、伪最近质心邻域分类器(Pseudo-nearest Centroid Neighbour Classifier,PNCN)[11]以及基于自归一化神经网络的候选体选择方法[12]等.上述方法中,依靠人类经验筛选的特征选择是影响脉冲星筛选2值分类结果的关键.不全面的特征设计方案可能会弱化模型的性能,所以特征设计问题尤为关键.此外,一些多方法集成的混合模型也取得显著效果[13–14].

在实际的大规模脉冲星数据计算和搜索中,由于输入数据集中大部分都是无标签数据,而且存在脉冲星与非脉冲星样本数据比例极不均衡的问题,导致使用有监督学习分类方法来识别脉冲星候选体的时间代价和工作量都相当大.本文在Rodriguez等[15]和Wang等[16]工作的基础上,提出一种基于混合聚类算法的脉冲星候选体筛选方案.通过基于滑动窗口的数据划分策略以及基于MapReduce模型的并行化设计,该方案在提高候选体筛选效率的同时,能聚类出更有参考意义的分类以促进特殊脉冲星的发现.在Parkes高时间分辨率宇宙脉冲星巡天(High Time Resolution Universe Survey,HTRU)数据集HTRU2[17]上与其他常用机器学习分类方法进行实验对比,结果表明所提出方案在精确度(Precision)和召回率(Recall)上均取得较优的结果,分别为0.946和0.905;根据Sun-Ni定理[18],当并行执行节点足够且通信代价可忽略时,该算法的总运行时间理论上会明显减少.

2 相关工作基础

实验数据集HTRU2来自澳大利亚Parkes望远镜的多波束(13个波束)的观测[9],所用脉冲星信号搜寻管道的DM值设定为0–2000 cm−3·pc,描述了在高时间分辨率宇宙勘测期间收集的基于PRESTO(Pulsar Exploration and Search Toolkit)软件处理的脉冲星候选样本数据.该数据集共包含17898个数据样本,其中16259个射频干扰(Radio Frequency Interference,RFI)虚假样本和1639个真实脉冲星样本,特征值包含脉冲轮廓的均值、脉冲轮廓的标准差、脉冲轮廓的超额峰度、脉冲轮廓的偏度、DM-S/N曲线的均值、DM-S/N曲线的标准差、DM-S/N曲线的超峰额度和DM-S/N曲线的偏度8个属性.HTRU2是一个开放的、样本相对丰富的数据集,认可度较高,因此被广泛用于评估脉冲星候选体分类算法的性能.

聚类是处理大型数据挖掘问题的关键方法之一,包含基于划分、基于密度、基于网格等聚类算法.K-Means[19]作为一种基于划分的聚类算法得到广泛应用.但原始K-Means存在聚类效果依赖于初始中心点的选择、只能应对数值型数据、异常值干涉大等缺陷.因此,不少学者一直在对该算法进行改进.Arthur等[20]提出一种选择尽可能相距较远的数据点作为初始中心的K-Means++算法,改进中心点的选择;Nguyen[21]提出K-modes算法用于解决K-Means只能应对数值型数据的缺点.基于密度的聚类方法,比如典型的DBSCAN(Density Based Spatial Clustering of Applications with Noise)算法[22],能发现任意形状的聚类,但聚类样本大、收敛时间长,对于簇密度不均匀情况聚类效果不佳.Rodriguez等[15]提出了一种基于密度峰值的快速搜索聚类算法CFSFDP(Clustering by Fast Search and Find of Density Peaks),其主要思想是簇类中心的密度应大于周围邻居的密度,且不同簇类中心之间的距离相对较远.由于该算法仅关注了密度较大且距离相对远的点作为中心点,容易将含有多个高密度点的同一簇类错误地分成多个簇类.为克服这个缺陷,Wang等[16]进一步提出一种基于密度层次划分的多中心密度峰值聚类算法McDPC(Multi-center Density Peak Clustering).

基于层次的聚类不需要预先指定聚类数且可以发现类的层次关系,但计算复杂度太高.本文借鉴国内外理论研究和实践应用的成功经验,就如何将这些不同聚类算法的优点有效结合并用于大规模候选体信号的聚类分析提出建议对策.

3 混合聚类算法

本文所提出的方法结合了基于密度层次和划分的聚类思想.首先,采用K近邻的多项式核(Polynomial)函数计算数据点密度(见下文(2)式),排除密度过小的离群点干扰;其次,结合密度峰值及层次思想,用于多密度簇类层次的划分,从而确定初始聚类中心点.再次,运用基于高斯径向基核(Radial Basis Function,RBF)距离的K-Means迭代进行数据点分配与簇中心优化.具体步骤如下:

步骤(1)进行数据预处理,通过主成分分析方法(Principal Component Analysis,PCA)对脉冲星观测数据进行特征选择和降维,从而得到特征向量为b的新特征空间输入数据集.可选的候选体物理特征值包括脉冲辐射(单峰、双峰和多峰)、周期、色散值、信噪比、噪声信号、信号斜波、非相干功率之和、相干功率等等.

步骤(2)数据点i和j之间的马氏距离由下式计算:

其中,T表示转置,S是多维随机变量的协方差矩阵,再根据上式计算各数据点基于K近邻的局部Polynomial核密度ρi.Polynomial核函数拥有的全局特性,使其泛化性能增强.

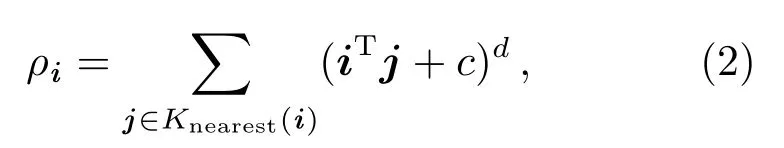
其中,Knearest(i)表示样本i的K个近邻对象构成的集合,c为偏置系数,d为多项式的阶.为消除数据变异大小和数值大小的影响,分别对d ij和ρi均采用离差标准化处理成D ij和Rhoi,如下.

其中,mind和minρ分别代表d ij和ρi的最小值,maxd和maxρ分别代表d ij和ρi的最大值.

步骤(3)根据(5)式剔除离群点.设定密度的阈值为threshold,inlier表示密度大于阈值的数据对象的集合.

再由(6)式计算非离群点之间的距离δi.δi表示inlier集合中,若对象i非该集合中的最大密度对象max(Rhoinlier),i到密度比它大且距离最近的样本j的距离.若i为最大密度对象,则表示i到密度比它小且距离最远的样本j的距离.剔除离群点有助于簇类中心点的选择.另外,密度过小的数据点数量少且分布边缘化.由于其稀缺性及低密度化,在数据分布中呈异常,而异常现象可能是纯噪声或特殊脉冲星.这部分数据后续将作进一步的确定.

步骤(4)所有距离δi大于某个已定义阈值(λ)的数据点可生成2维决策图,例如,1组随机生成数据的2维决策图如图1所示,其中,横轴表示密度Rhoi,纵轴表示距离δi.

假定对该2维决策图实例的Rhoi轴和δi轴分别按照大小为θ和γ的间隔进行划分,如图2所示.

若在Rhoi轴或δi轴划分区域包含两个或两个以上的无数据点存在区域,则称该空隙区域为空区.在图2(a)和2(b)中,空区把所有的数据点划分为两个密度区域,将最右的密度区域称作最大密度区域,其余为低密度区域.

在低密度区域,由于区分度不高,将该低密度区域相应的小簇均合并成一个簇类;在最大密度区域,若所有的代表点都在同一个δi区域,则将这些代表点均选作独立的簇类中心;若代表点不在同一个δi区域,则这些代表点间距离区分度不高,可能属于同一个簇类,因此需要将相应的小簇合并成一个大簇.

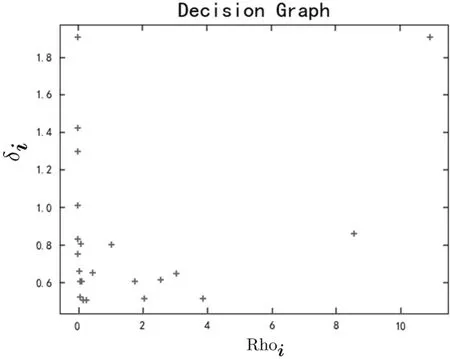
图1 决策图实例Fig.1 Example of decision graph

步骤(5)确定簇类数k以及对应集群C m(1≤m≤k)的中心centerm.

步骤(6)根据就近原则将各个数据点i分配给距离最近的centerm所在簇类,相似性度量方式采用RBF核距离,如(7)式所示.RBF核函数拥有局部特性且学习能力强,通过RBF核距离可实现对i和j间测度距离向高维空间的转换.

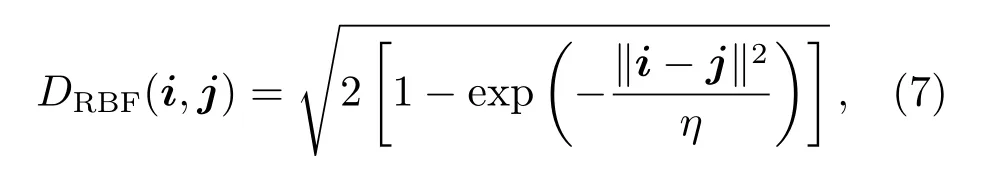
其中,η代表核函数宽度.按照(8)式计算新簇内数据点均值作为新的中心center′m,n m表示属于的数据点总数.

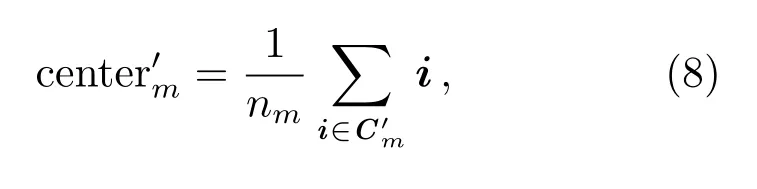
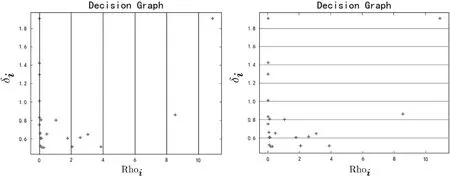
图2 随机生成数据集的Rho i划分和δi划分.左:Rho i划分;右:δi划分.θ=2,γ=0.2.Fig.2 Rho i andδi division of randomly generated data set.Left:Rho i division;Right:δi division.θ=2,γ=0.2.

步骤(7)计算数据集所有对象的误差平方和SSE:

直到SSE值不再发生变化,算法停止,否则回到步骤(6).

整体算法流程图如图3所示.

4 并行化设计

4.1 基于滑动窗口的数据集划分策略

为划定更全面的脉冲星识别范围,根据数据结构最大化地准确筛选候选体,采用滑动窗口理念[23]进行数据划分,将数据划分为L个数据块,每个数据块表示为Block(o)(1≤o≤L).拟通过从真实样本中挑选一组较完备的各类脉冲星候选体特征数据作为样本,用v表示,每轮划定Batchsize=w的窗口,按特定比例(v:w)加入到待检测数据,w表示滑动窗口Batchsize数.滑动窗口数据分配方法如图4所示.目前,聚类存在一基本假设,即处在相同聚类中的示例有较大的可能拥有相同标记.因此,根据各类数据分布的稠密或稀疏区域设定决策边界,从而确定脉冲星数据分布区域,进行对脉冲星信号与非脉冲星干扰信号的区域划分.通过计算各簇内部脉冲星样本分布密度以统计相似程度,选取脉冲星样本占有率大于某个比例的簇进入脉冲星候选体列表;聚类流程步骤(3)所排除的噪声点则有可能是特殊脉冲星.

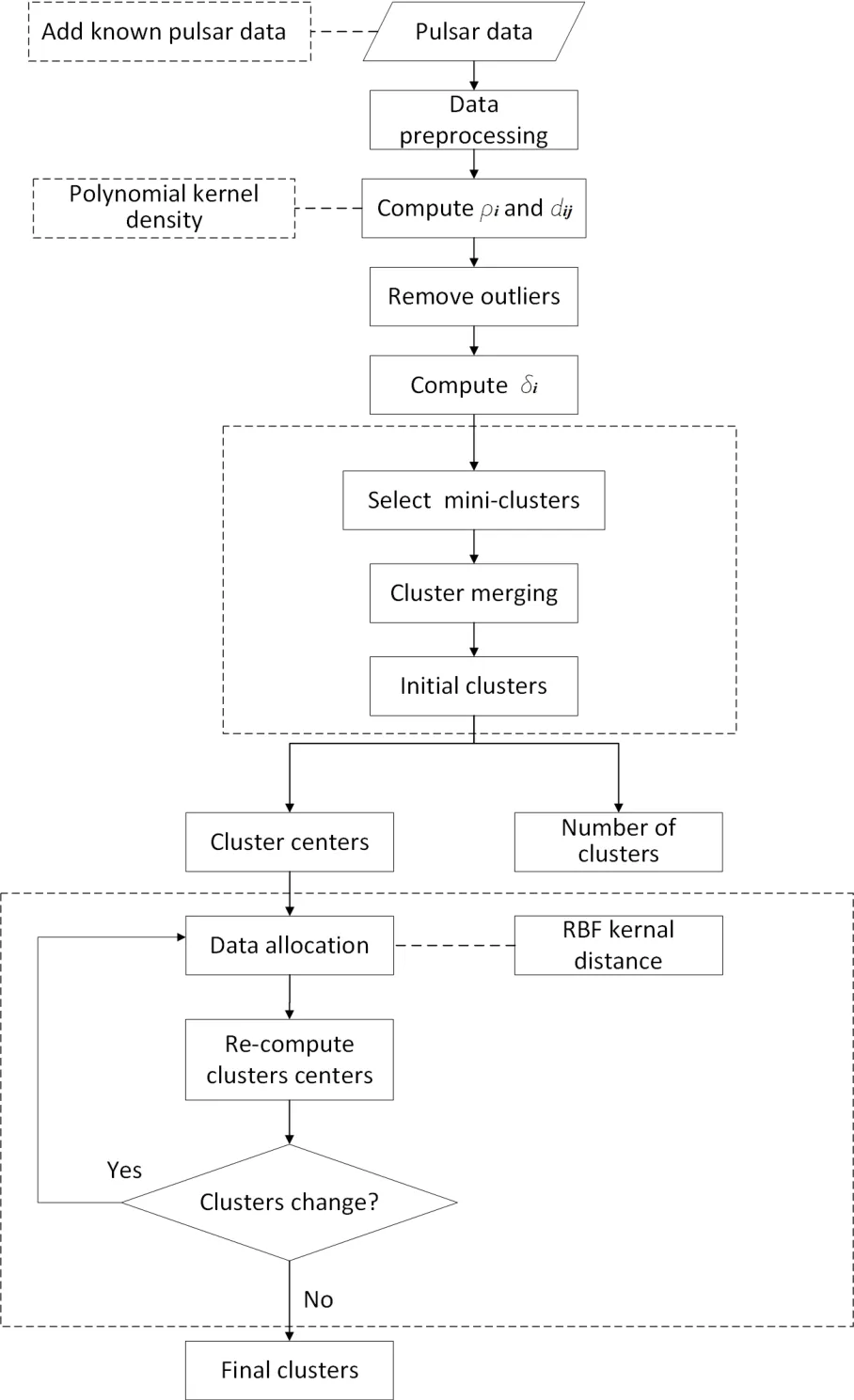
图3 混合聚类算法的流程图Fig.3 Flow chart of hybrid clustering algorithm

4.2 基于MapReduce/Spark模型的并行化设计方案

针对大规模的脉冲星数据处理,依据Sun-Ni定理,研究该聚类算法在实现MapReduce计算模型的并行化时是非常有必要的.一方面,可提高聚类结果的精确度;另一方面,能够降低数据比较的次数.Sun-Ni定理中引入了一个函数G(p)表示存储容量受限时工作负载的增加量,p表示并行节点数.该定律提出在满足固定时间加速比所规定的时间限制的前提下且拥有足够的内存空间时,对问题进行缩放能有效地利用内存空间.图5是基于MapReduce/Spark模型的并行化设计流程图,首先通过上述基于滑动窗口的方法将数据划分为L个数据块后并行执行.下一步,由Map1和Reduce1函数完成Block(o)(1≤o≤L)中数据点的密度计算以及初始聚类中心点(cluster centers)的选取.需要说明的是在Map阶段的输入项中,key是行号,value是当前样本各维度的值组成的列表.而在Reduce阶段的输出中,key.id即初始聚类中心.最后,Map2和Reduce2函数迭代完成Block(o)内每个数据点到cluster centers(o)的距离计算并重新标记其所属簇类(每个簇C m均有对应编号).其中用Reduce2函数计算出新的簇中心为下一轮聚类任务作准备.比较当前轮簇中心与上一轮对应簇中心之间的距离,若变化小于给定的阈值,则运行结束;否则将新簇中心作为下一轮的聚类中心.在聚类结束后,提取出脉冲星簇和噪声点.Spark作为一种大规模数据处理通用的计算引擎,其计算过程与MapReduce类似.

5 实验对比分析

单机实验的硬件环境为:处理器Intel Core i7-9700K@3.6GHz,内存48GB DDR4 3000 MHz,显卡Nvidia GeForce RTX 2080 Ti;软件环境为:Windows 10 64bit系 统 下Anaconda4.8+python3.8+numpy1.18.5框架.

5.1 数据划分

实验采用公开数据集HTRU2,其中共包含1639颗真实脉冲星样本和16259个由RFI产生的虚假样本.从该数据集的1639颗已知脉冲星中随机选取1600颗作为脉冲星样本集s,而剩余39颗被随机混入到虚假数据样本中形成待检测数据集.根据4.1节的数据划分策略,将滑动窗口大小Batchsize设置为2,单位大小为1161,待检测数据集按Batchsize被均分为(t1,t2,...,t13,t14),由此实验数据划分为{Block(1):[s,t1,t2],Block(2):[s,t2,t3],...,Block(13):[s,t13,t14],Block(14):[s,t14,t1]}共14个数据块.各个Block(i)分别进行聚类,当聚类完成后,选取脉冲星样本占有率≥50%的簇进入脉冲星候选体列表.

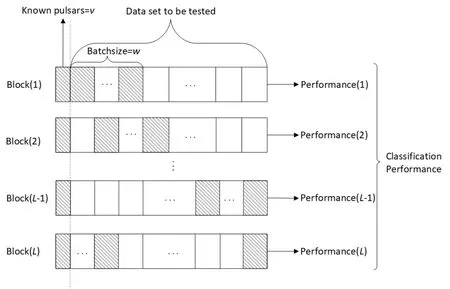
图4 基于滑动窗口的数据分配Fig.4 Data distribution scheme based on sliding window

5.2 评价指标

候选体分类常采用准确率(Accuracy)、精度(Precision)、召回率(Recall)和F1-分数(F1-Score)4个指标对算法进行评估.Accuracy能大致反映整体判断正确与否,但当数据不均衡时并不能客观地反映分类的性能.Precision用于判断正类样本数中真实正类样本数所占之比,Recall则是判断正确的正样本数与所有正类样本数之比.由于聚类的Precision和Recall往往相互矛盾,所以可选取F1-Score来综合度量这两个指标.表1表示分类的混淆矩阵.

结合4.2节并行化设计方法,则实验的评价指标采用总体Precision、Recall和F1-Score设定如下:

其中,TP表示被正确归类为正样本的数量,FN是被错误归类为负样本的数量,FP为被错误归类为正样本的数量,TPo、FNo和FPo则分别表示L个数据块中第o个数据块的TP、FN和FP值,UTP=TP1∪TP2∪TP3···TPL代表每个小数据块识别脉冲星的并集,Recallo和Precisiono分别表示单个数据块的召回率和精度,Recalltotal则表示实验的总体召回率.

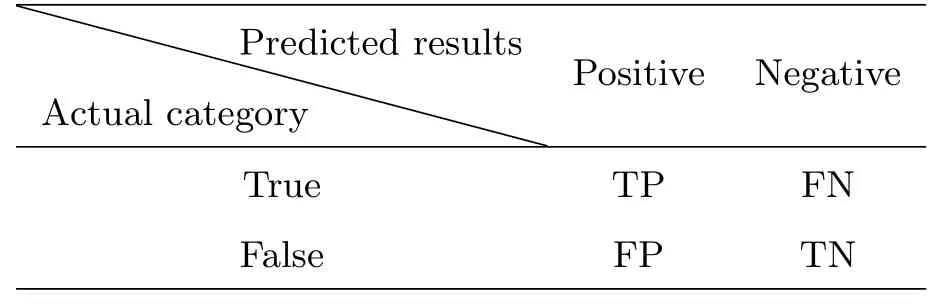
表1 混淆矩阵Table 1 Confusion matrix

5.3 参数设置

实验涉及的参数包括计算数据点密度的K近邻参数,密度的阈值threshold,Polynomial核参数c和d,RBF核参数η,筛选小簇的阈值λ,对密度区域划分的θ值以及对距离区域划分的γ值.具体设置如表2.

表2 算法参数Table 2 Parameters of algorithm

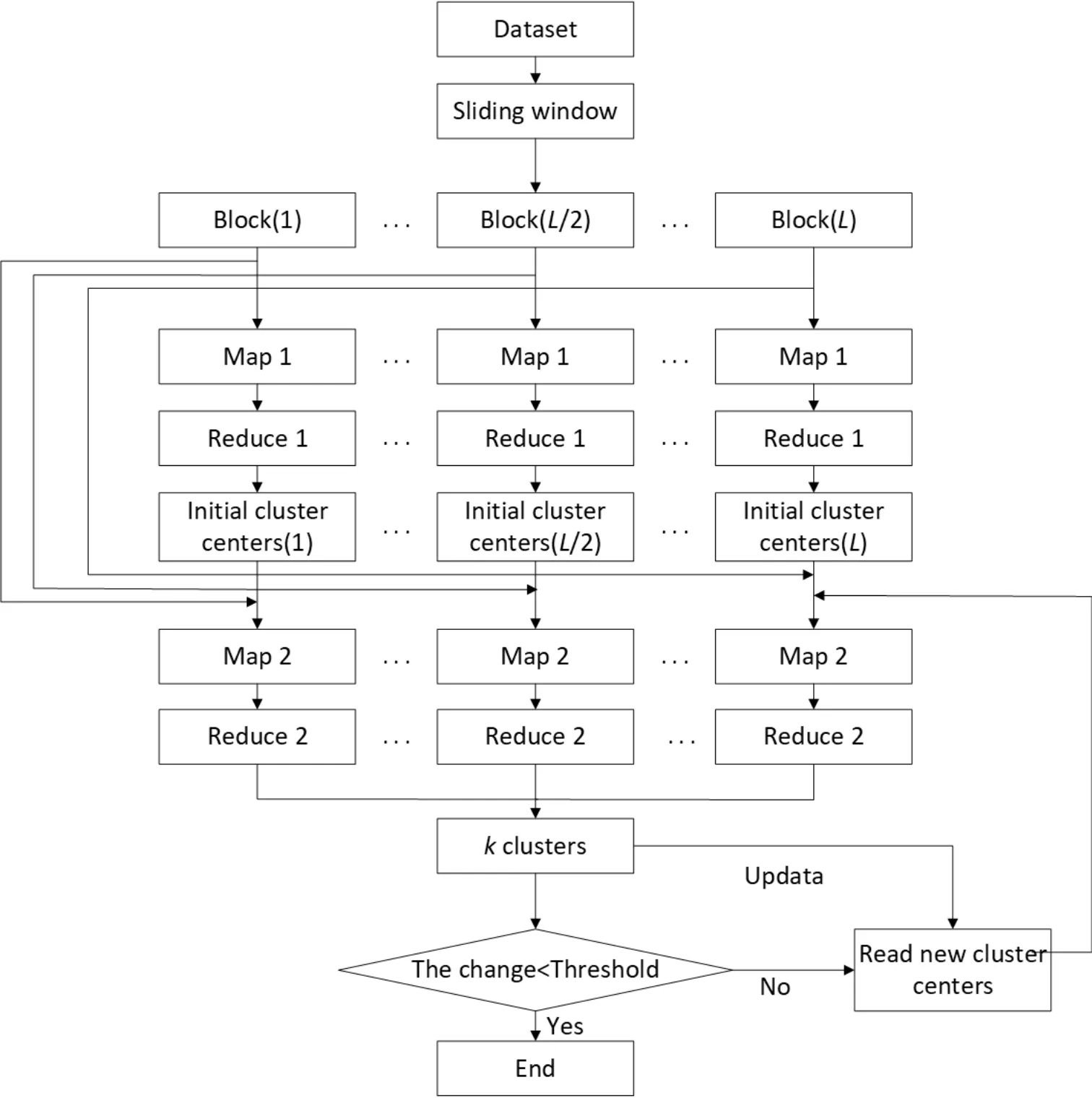
图5 MapReduce流程图Fig.5 Flow chart of MapReduce

5.4 聚类结果分析

表3显示了不同监督学习和无监督学习算法在HTRU2数据集上的性能对比.在无监督算法中,混合聚类算法具有最高的Recall值即90.5%.与有监督学习算法相比,该算法的Recall值仅低于GMO SNNNNNNNNN (Genetic,Synthetic Minority Over-sampling and Self-normalizing Neural Networks)[12],F1-Score低于GMO SNNNNNNNNN、Random Forest[24]和KNN(K-Nearest Neighbor)[25]算法,但高于SVM(Support Vector Machines)[11]和PNCN[11].另外,经多轮的对照实验(每轮随机挑选出39颗脉冲星形成待检测数据集),得出被该算法检测出的脉冲星数最高一次达到36颗,均值为34颗.由于混合聚类的无监督学习和快速收敛的优点,适用于大规模脉冲星数据快速分类挖掘的场景.实验结果表明,所提出的基于混合聚类的方案具有可行性和有效性.在实际脉冲星搜索场景下,随着相关参数、脉冲星样本集以及数据划分策略的优化,其聚类效果将进一步提升.

5.5 时间复杂度分析

设实验数据集的样本数为n,所提出算法与McDPC[16]、PNCN[11]的时间复杂度如表4所示.对于McDPC,计算ρi和δi时间复杂度为O(n2),基于不同密度水平的聚类时间复杂度也为O(n2),所以整个算法的时间复杂度为O(n2);PNCN时间复杂度取自其最坏情况下的计算量O(2nM K+F M K2/2),M为元素的特征数,F为类别数,M和F设定为常量.所提出混合聚类算法在不使用4.1、4.2节的并行化方案的情形下,其串行时间复杂度为O(n2+nk H M),H为迭代次数.由于k、H、M为常量,其复杂度简化为O(n2),这接近于McDPC但比PNCN高.然而,若运行在所设计的并行模型上,依据Sun-Ni定理,其复杂度变为O((G(p)z)2),其中G(p)为因子,z为Block(o)的样本个数且z≪n;当并行节点数p足够(p值趋近于被划分的数据块L达到某个阈值)且通信开销可忽略时,G(p)→1,即复杂度趋近于O(z2).可见,该算法的并行化方案理论上在确保聚类效果的同时较大地改善了算法执行时间.

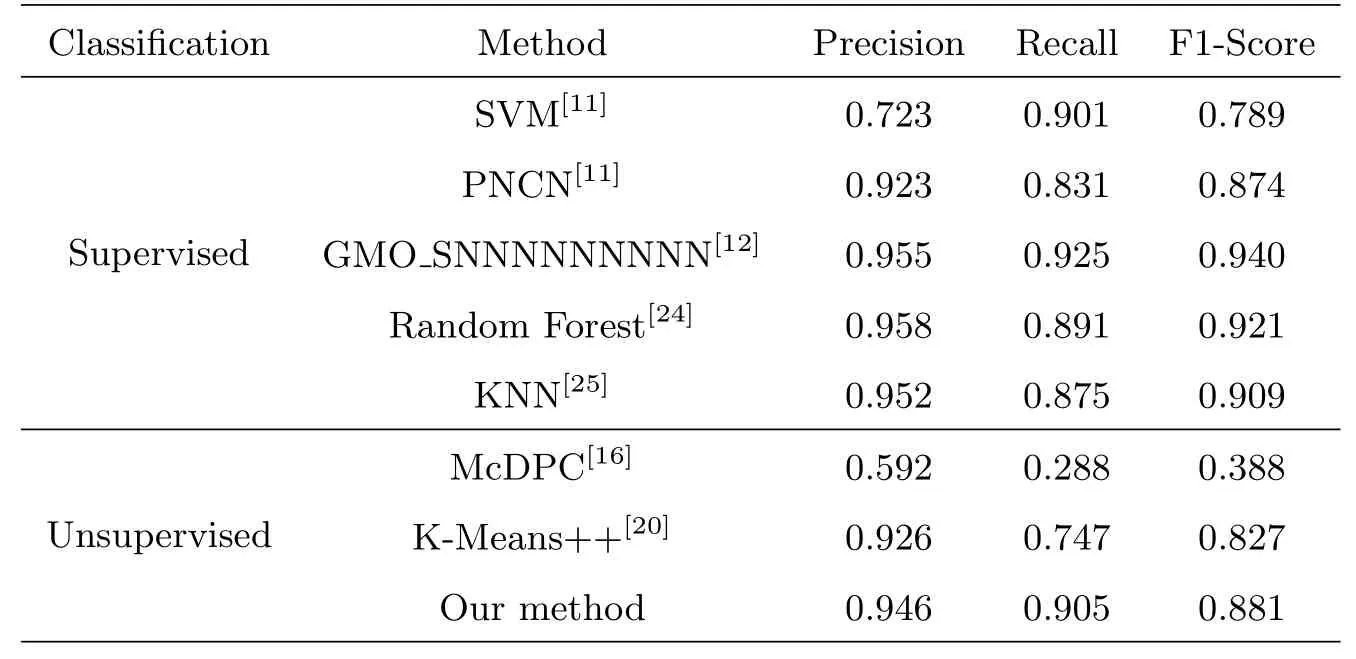
表3不同方法在HTRU2数据集上的效果Table 3 Results with different methods on HTRU2 data set

表4 算法复杂度Table 4 Time complexity statistics of various algorithms

6 总结与展望

为解决FAST天文大数据背景下的脉冲星候选体智能筛选问题,提出一种基于混合聚类分析算法的快速筛选方案.其新颖之处在于,结合了基于密度层次和划分的聚类方法的特点以提高聚类性能;为更好展现数据间分布的“疏密程度”,体现聚类结果中不同簇的数据结构差异,采用K近邻的局部Polynomial核函数方法改善密度计算,并且利用RBF核函数将数据转化至高维空间进行相似性度量;通过基于滑动窗口的分组策略与MapReduce/Spark并行化设计,进一步提升筛选召回率并减少执行时间.

对比实验分析和时间复杂度分析,证明所提出方案具有可行性和有效性,随着实际场景中数据分组与相关参数的优化,其各项性能指标会有更大提升.无监督聚类方法更适用于大量无标签数据集的分类以及脉冲星与非脉冲星样本数据比例极不均衡情形.下一步,将通过较完备的FAST实验数据继续对混合聚类方案进行改进;另一方面,研究该方案接入到PRESTO脉冲星搜索流程pipeline进行实际测试,为FAST观测的大量候选体信号筛选提供理论和实践参考.