含夹杂物轴承钢中裂纹的萌生与扩展

罗敏，汪久根，冯毅雄，冯照和

(1.浙江大学 机械工程学院，杭州 310027；2.杭州汽轮机股份有限公司，杭州 310022)

0 引言

轴承作为机械旋转体的支承结构，是工业机械中应用广泛的部件，研究滚动轴承的裂纹萌生、扩展方式及疲劳寿命对保证其可靠性至关重要。在轴承滚动接触表面光滑且润滑条件适合的情况下，轴承次表层微裂纹扩展引发的层裂在滚动接触疲劳失效中占主导地位。次表层的裂纹萌生往往始于材料缺陷，特别是夹杂物引发的应力集中现象促使裂纹萌生与扩展。因此，围绕轴承次表层分布的夹杂物展开研究，建立轴承滚子与滚道接触区仿真模型进行模拟具有一定的工程意义。

分析应力对接触疲劳的贡献，经历了静态应力、最大剪应力、最大正交剪应力与Mises应力的发展过程，目前常用Mises应力分析滚动接触疲劳失效。裂纹的萌生与扩展过程十分复杂且具有随机性，需用统计分析方法研究。轴承滚动体与内圈滚道的滚动接触过程中发生疲劳损伤累积，会在次表层萌生微裂纹，多个微裂纹的联合形成了向表面扩展的较长裂纹，裂纹到达表面产生剥落。文献[1]综述了非金属夹杂物对滚动轴承疲劳寿命的影响，介绍了麻点和剥落2种疲劳失效类型的理论分析方法和试验测试技术。

关于接触疲劳的研究已有80多年的历史，提出了多种方法分析夹杂物对疲劳过程的影响：文献[2]提出用最大能量释放判据来分析夹杂物边界上的裂纹萌生过程，建立了弹塑性多轴疲劳裂纹萌生有限元模型，对滚动接触疲劳裂纹的萌生寿命进行预测；文献[3]用Eshelby张量分析夹杂物的影响；文献[4]用格林函数分析夹杂物对材料力学性能的影响。

近年来，文献[5-15]较系统地分析了夹杂物对接触疲劳的影响：文献[5-6]用计算几何的方法分析了材料的拓扑随机性和材料性能的随机性对韦布尔分布斜率的影响，分布斜率1.29～3.36时，疲劳寿命与最大赫兹接触应力的9.35次方成反比；文献[7-8]分析了晶粒间的疲劳损伤累积，认为晶粒的边界对剥落失效与疲劳寿命的离散性有显著的影响；文献[9]建立三维有限元模型分析微观结构对滚动接触疲劳的影响，这与球轴承的接触问题一致；文献[10-11]用弹塑性有限元模型结合碳弥散模型分析了白层的产生及其方向，模拟了马氏体的退化，认为在应力集中区域中萌生裂纹；文献[12-13]模拟分析了夹杂物周围蝴蝶状裂纹的形成、萌生与扩展过程，与试验结果相吻合；文献[14] 提出一种结合损伤力学的内聚力模型，用于模拟多晶轴承钢在滚动接触循环加载下的裂纹萌生与扩展，模型中的损伤在晶界由内聚力元素受损断裂引发，最终获得的层裂方式和疲劳寿命分布与公开文献中的结果相符；文献[15]建立了基于连续损伤力学的有限元模型，研究深沟球轴承的滚动接触疲劳寿命，建立了相关寿命方程。这些工作为揭示滚动疲劳机理提供了新的认识，然而，针对轴承钢疲劳寿命的准确计算仍需进一步研究。

文献[16]分析了非金属夹杂物深度、径向载荷、表面摩阻力和滚道曲率半径对表面裂纹萌生的作用，径向载荷和表面摩阻力对裂纹萌生有显著的影响，而滚道曲率半径对裂纹扩展的方向没有影响。文献[17]试验分析了裂纹的萌生与扩展阶段，认为在早期就萌生了裂纹，并且主要是裂纹扩展阶段决定了疲劳寿命的长短。滚动接触疲劳不仅是滚动轴承的重要问题，对于列车的轮轨接触、摩擦无级变速器的寿命也是重要问题。文献[18] 研究了温度、摩阻力系数、材料的晶粒大小和接触应力对轨道接触疲劳的影响。目前，有限元分析已经是研究滚动接触疲劳的重要方法。

本文基于内聚力模型的损伤起始准则和损伤演化规律，利用VUMAT子程序结合连续损伤力学构造了新的损伤演化方式，实现循环加载下的损伤累积，拟建立基于内聚力模型的疲劳损伤累积失效模型，模拟含夹杂物轴承次表层裂纹从萌生至扩展到接触面的动态过程，以更好地分析、预测含夹杂物轴承钢滚动接触时的裂纹萌生与扩展，并且分析载荷和摩擦因数对裂纹萌生与扩展过程的影响。

1 基于内聚力模型的裂纹萌生与扩展模拟

1.1 内聚力单元的损伤起始准则

内聚力模型遵循的断裂准则为牵引-分离定理，通过应力-张开位移曲线定义单元失效方式。内聚力模型的双线性本构关系如图1所示，图中Tmax为内聚力单元进入损伤阶段前的最大牵引力，K0为单元刚度，GIC为材料断裂能，δin为损伤起始点，δfail为失效断裂点。牵引力为内聚力单元受到外部应力F作用后反馈的单元内力，用来维持单元的完整性。在起裂阶段，随着牵引位移δ的不断增加，牵引力随之增加,达到损伤起始点δin后，材料进入损伤阶段，材料刚度退化，对内聚力单元的拉力增大，反馈的牵引力反而减小，直到牵引位移达到δfail，牵引力减小到0，单元断裂失效。

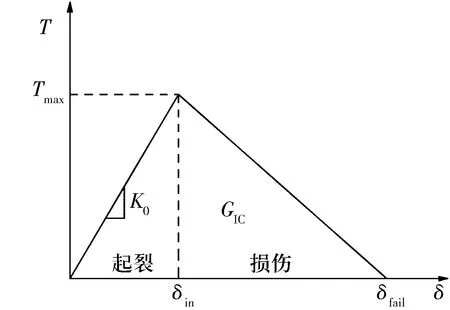
图1 内聚力模型的双线性本构关系

1.2 基于连续损伤力学的疲劳损伤累积过程

损伤演化模型用于描述内聚力单元进入损伤阶段后材料不断退化，内部牵引力不断下降至0的过程。为模拟高周循环载荷作用下的疲劳损伤累积失效过程，在材料本构应力应变关系中引入一个基于连续损伤力学的变量D，定义为材料的损伤变量，用于降低材料的刚度。初始牵引位移为0时材料没有损伤，此时初始总损伤值D为0；当材料完全损伤时，总损伤值D为1。

高周疲劳的内聚力模型认为总损伤为静态过载损伤和动态循环疲劳载荷损伤之和。单元静态损伤值D1可采用内聚力单元自带的基于位移的损伤演化来表示，定义动态循环疲劳损伤值为D2，获得总损伤值D为

D=D1+D2。

(1)

内聚力模型自带的基于位移的损伤演化是静态线性的，可表示为

(2)

当δ=δin时材料刚进入损伤阶段，D1=0，单元开始损伤；δ=δfail时单元损伤结束，D1=1，单元失效。

对于D2，由于轴承的高周疲劳中微观晶粒的塑性应变很小，假设这种疲劳损伤为准脆性损伤，非线性方程的广泛通用形式为

(3)

式中：N为循环次数；Δσ为相关应力的变化范围；τs为晶界的抗应力；σm为法向平均应力；m为损伤定律指数。

由于本文所研究的轴承滚子与内圈滚道接触模型的载荷为压力，因此单元节点均处于压缩状态，主应力对该模型主要产生的Ⅱ型滑开裂纹的扩展只能起到抑制作用。可假设沿单元切向作用的剪应力是造成疲劳损伤、裂纹萌生与扩展的唯一应力，此时法向平均应力σm对剪切裂纹的形成没有影响，由此可得动态循环疲劳损伤值D2的损伤演化方程为与切向应力有关的函数，即

(4)

式中：Δτs为作用于单元的切向应力变化范围。

则内聚力单元内部反馈的牵引力为

T′=(1-D)Tmax，

(5)

内聚力单元的刚度为

K′=K(1-D)，

(6)

式中：T′为材料损伤后内部牵引力;K′为材料损伤后更新的单元刚度；K为单元初始刚度。

在高周疲劳循环中，为提高计算效率采用Lemaitre提出的“jump-in cycles”算法，该方法已广泛用于基于连续损伤力学的滚动接触疲劳模拟。假设在损伤值增量ΔD为定值的前提下，一定的循环次数ΔN内应力变化范围保持不变，如图2所示。在每个循环段ΔN结束后对内聚力单元刚度K和总损伤值D进行更新，直到总损伤值D达到1，判断该内聚力单元失效。

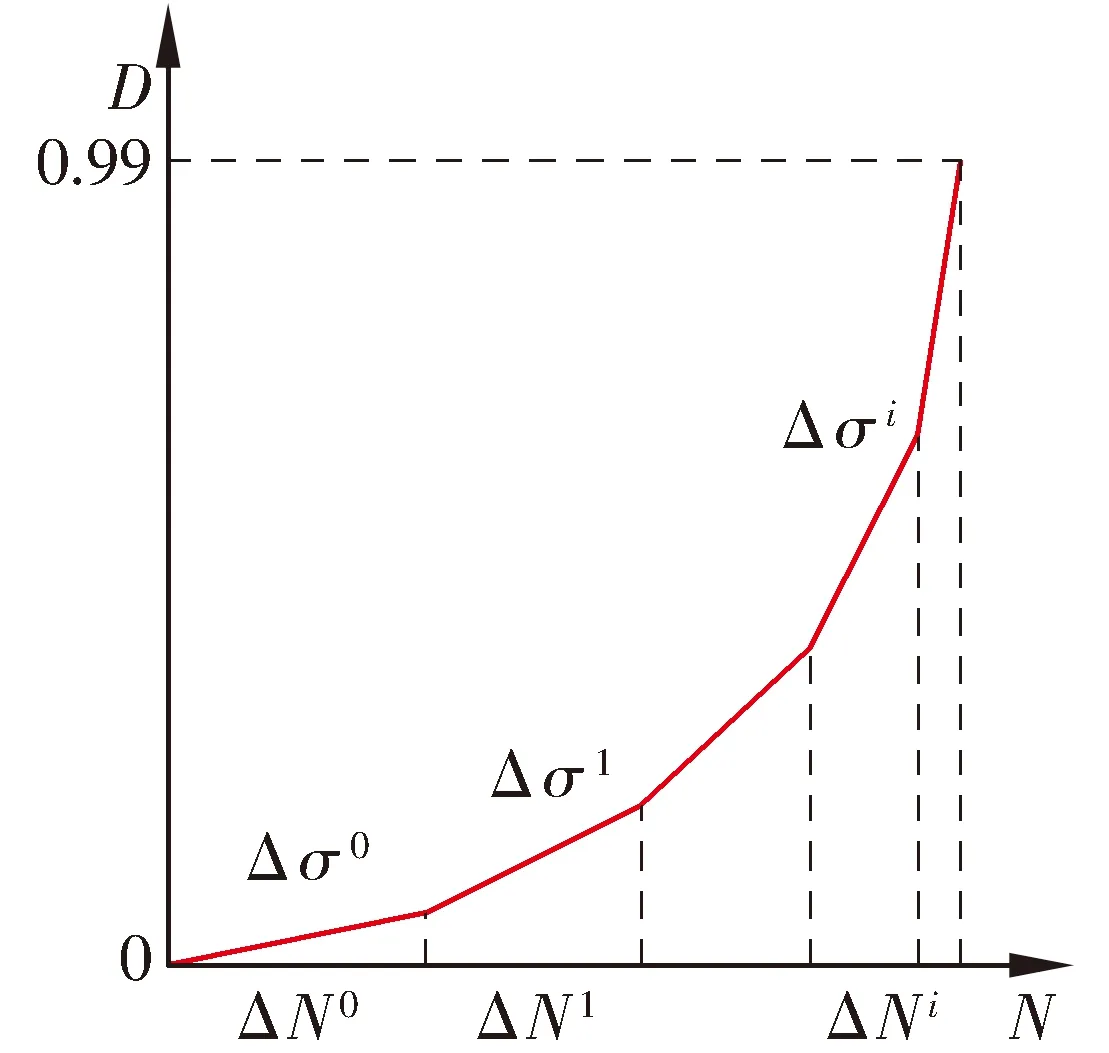
图2 分段线性损伤演化过程

选择损伤增量ΔD为0.2，疲劳累积失效模型的损伤演化步骤如下：

1)将每个内聚力单元的初始总损伤值和初始循环次数设置为零，即

(7)

式中：j为第j个单元,j=1,2,…,n；i为第i个循环段,i=1,2,…，n；n为内聚力单元个数。

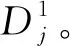
3)计算每个内聚力单元的动态疲劳损伤速率，即

(8)

4)选择具有最大动态疲劳损伤速率的内聚力单元作为当前循环段i的临界单元，即

(9)

5)当前循环段i中的循环数为

(10)

6)此时循环次数为

N=N+ΔNi。

(11)

7)在下个循环段开始时，内聚力单元的损伤值更新为

(12)

单元刚度更新为

(13)

重复步骤2—7，直到损伤值D达到临界值1判断单元失效。当内聚力单元失效时，单元内部分离，认为微裂纹在该失效位置处萌生，此时的循环次数Nin即裂纹初次萌生阶段。该循环过程持续进行，将有新的单元失效，可以模拟裂纹的扩展行为。直到当前失效单元存在z坐标为0的节点，即微裂纹扩展至轴承滚道表面时，认为将在该位置发生剥落现象，此时的循环次数Nfail即轴承总寿命。

2 有限元模型

2.1 轴承滚动接触有限元模型

滚子与内圈的滚动接触中，可将圆柱滚子轴承的内圈表面扩展成无限半空间，将滚子与滚道之间的法向接触等效模拟为赫兹接触，得到分布载荷为

(14)

式中：x为接触点的横坐标；a为接触半宽；pmax为最大接触应力。

采用ABAQUS软件建立NU308型内圈无挡边圆柱滚子轴承滚子与滚道接触区仿真模型，在模型中距离表面0.5a深度处设定直径为20 μm的圆形夹杂物，模型参数见表1。

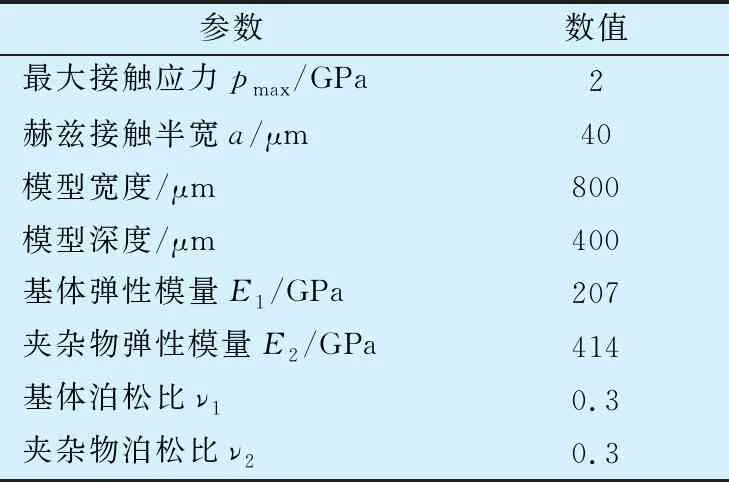
表1 仿真模型参数

2.2 模型载荷、边界及材料参数

研究滚动接触疲劳损伤累积导致的裂纹萌生与扩展过程，需要模拟滚子在内滚道上循环滚动的运动过程。如图3所示，通过使表面压力分布载荷在接触面上x轴坐标为-2.5a～2.5a区域内，以离散的步骤单向从右向左移动进行模拟，施加载荷的有效区域为-2a～2a，将一次循环分解为多个离散载荷。移动载荷的法向分量为

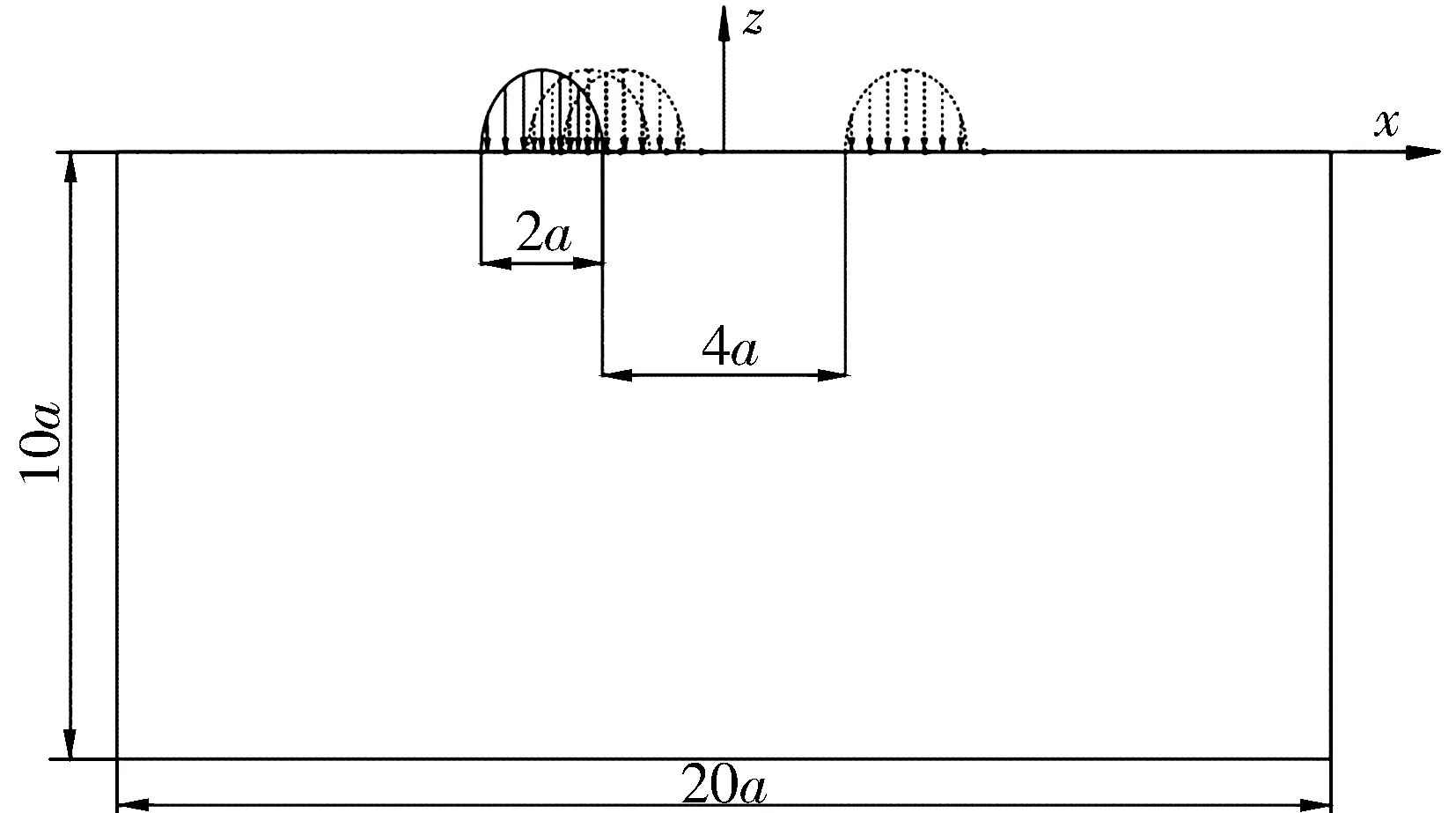
图3 滚动接触模拟载荷示意图

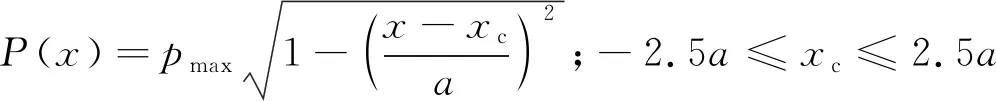
(15)

式中：xc为载荷中心的横坐标。

移动载荷的切向分量方向为从左向右，可表示为与法向分量相关的函数，即

t(x)=fμP(x)，

(16)

式中：fμ为摩擦因数。

将模型表面-2a～2a区域分割为10块，第1个分析步为第1块区域施加载荷，载荷分布方式为自定义场，以此进行每个分析步的载荷设置，并设置上个分析步的载荷不传递到下个分析步；以同样的方式在每个分析步中设置表面切向载荷。边界约束方式为模型底部完全固定，模型左右边界约束x轴方向自由度，在模型所有单元间插入厚度为0的内聚力单元。

内聚力单元的最大牵引力Tmax与钢材屈服强度相关，其弹性模量、剪切模量、密度与钢基体材料相同。计算获得相关参数，并结合GCr15的S-N曲线获得(4)式中参数τs和m的值，见表2。获得滚动轴承赫兹接触内聚力有限元模型，如图4所示。

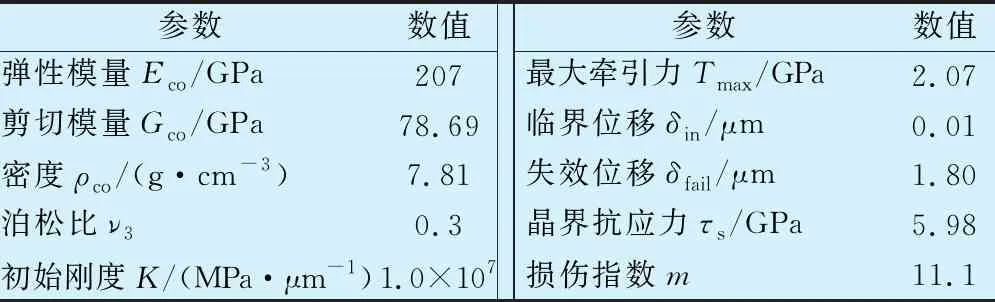
表2 内聚力单元参数

图4 滚动接触内聚力模型

2.3 损伤累积有限元分析流程

ABAQUS自带的内聚力模型在受载损伤过程中只考虑了静态过载损伤，需要通过子程序VUMAT将基于连续损伤力学的动态循环疲劳损伤与静态过载损伤结合，并联合ABAQUS自带的python脚本端口，提取每个循环段加载后ABAQUS程序计算结果ODB文件中每个单元的总损伤值、应力、刚度作为下个循环段的初始值，生成新的inp文件并提交ABAQUS进行下个循环段的计算。损伤值等于1时认为单元失效，子程序中根据损伤值更改状态变量并传入主程序进行单元删除，继续判断失效单元的节点z轴坐标是否等于0，不是则进入下个循环，是则结束循环,输出完整的疲劳损伤过程，分析流程如图5所示。

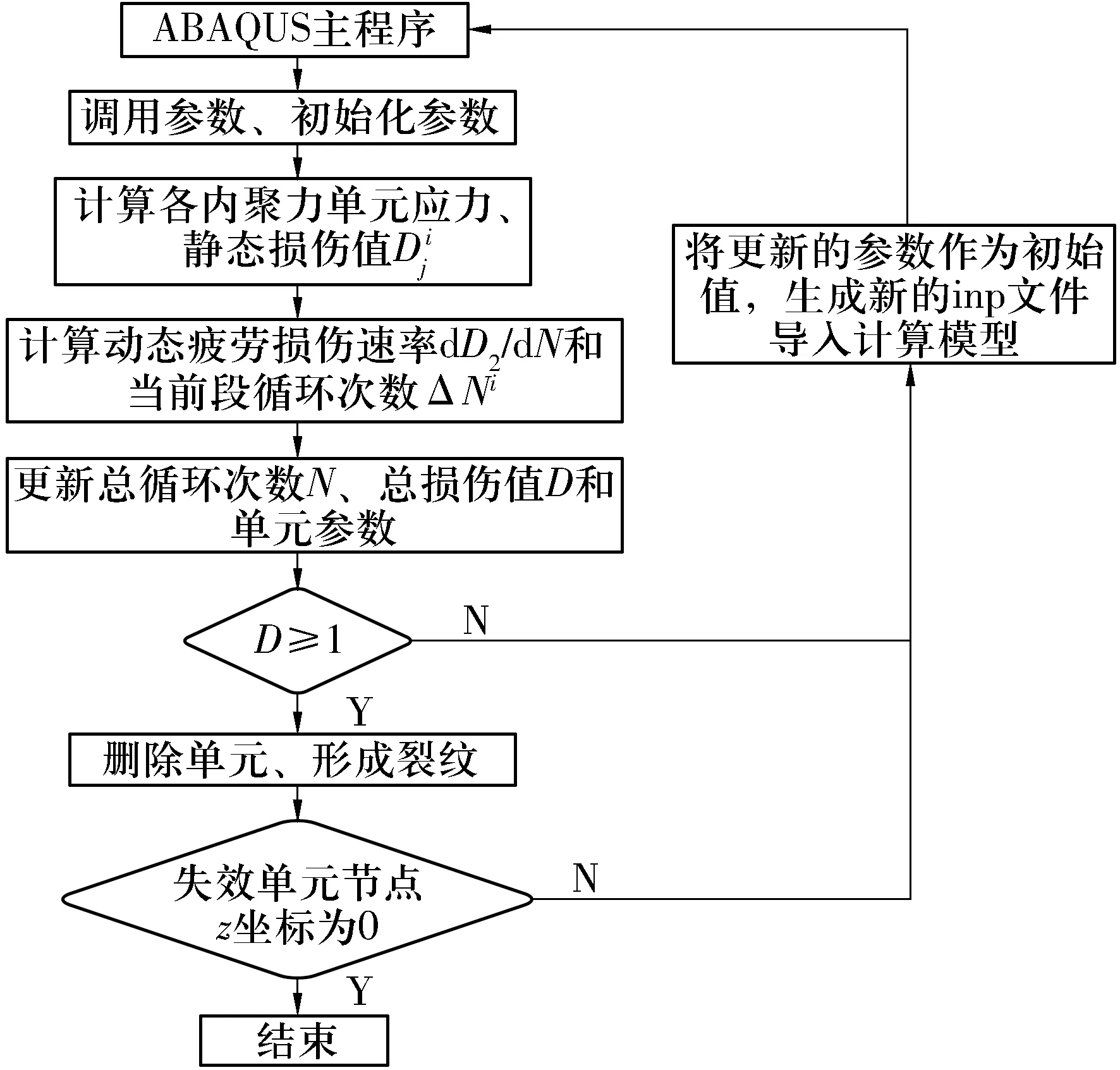
图5 损伤累积有限元分析流程

3 仿真结果与讨论

3.1 裂纹的萌生与扩展

有限元模型的仿真结果如图6所示。全过程包括裂纹的萌生、扩展、进一步扩展以及扩展至表面。

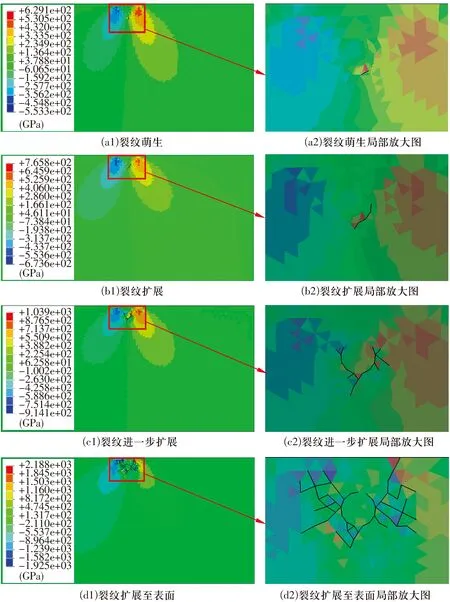
图6 疲劳裂纹的萌生与扩展(pmax=2.0 GPa)

随模型受载循环次数的增加，循环次数Nin为3.23×106时萌生了第1条裂纹，所处位置为夹杂物周围。随着循环过程继续，多个内聚力单元失效，初始微裂纹围绕夹杂物逐渐扩展且萌生了新的裂纹分叉。裂纹逐渐扩展为更长的裂纹并向表面延伸，循环次数Nfail为17.92×106时裂纹扩展到轴承滚道表面，预计将会在表面形成椭圆形剥落。裂纹扩展时期的循环次数占总循环次数的81.97%。这与文献[11,14]的轴承滚动接触仿真模型研究结论一致，与文献[17]的试验观测结果也基本相符，认为在接触应力较低的高周循环中，滚动接触的疲劳裂纹扩展阶段平均寿命占总寿命的比例较大。

3.2 载荷对裂纹萌生与扩展的影响

考虑载荷对裂纹萌生与扩展的影响，将载荷增大到2.5 GPa，仿真结果如图7所示。随着模型受载循环次数的增加，循环次数Nin为1.06×106时萌生了第1条裂纹，所处位置为夹杂物周围；循环次数Nfail为2.32×106时裂纹扩展到轴承滚道表面。裂纹扩展时期的循环次数占总循环次数的54.31%。相比载荷为2.0 GPa的情况，载荷增大为2.5 GPa后,裂纹萌生位置与扩展方式基本不变，但裂纹扩展寿命占总寿命的百分比明显减小。

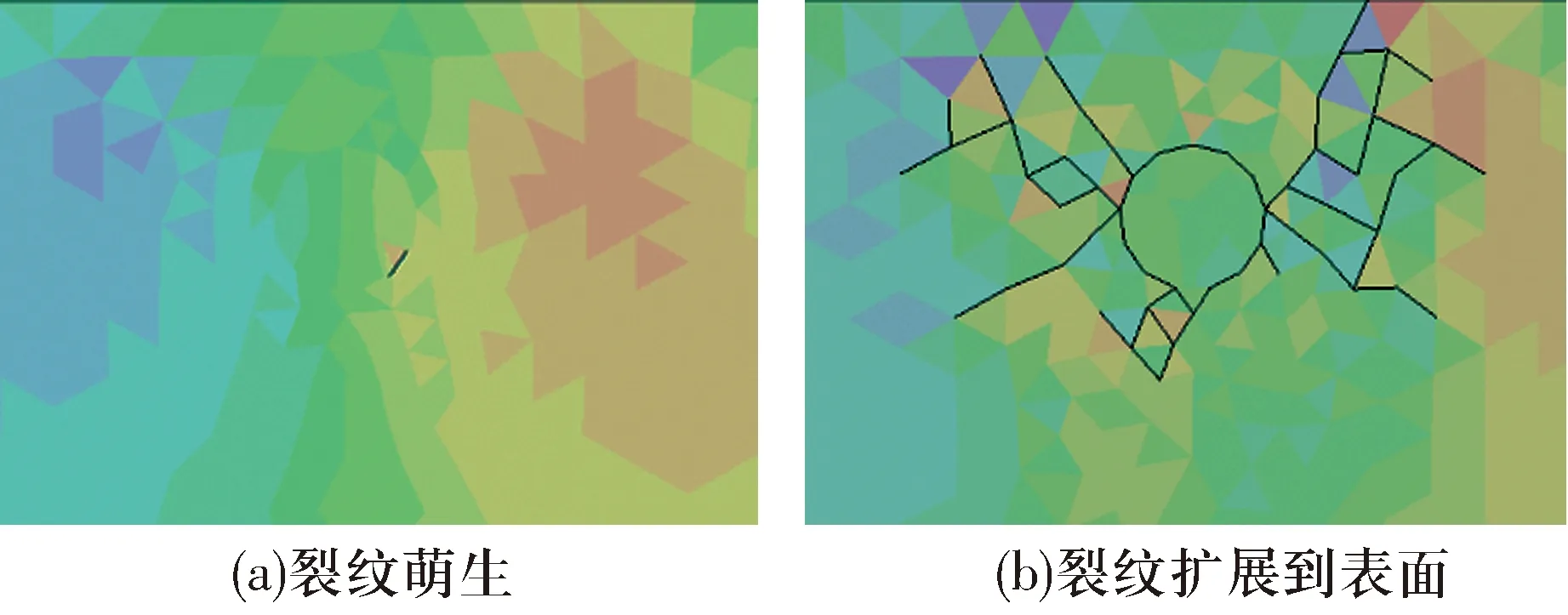
图7 更高载荷下疲劳裂纹的萌生与扩展(pmax=2.5 GPa)

3.3 摩擦因数对裂纹萌生与扩展的影响

考虑摩擦因数对裂纹萌生与扩展的影响，将摩擦因数增大到0.15，仿真结果如图8所示。循环次数Nin为3.02×106时萌生了第1条裂纹，所处位置相比摩擦因数为0.05时相对表面距离明显减小，位于夹杂物顶部；循环次数Nfail为12.74×106时裂纹扩展到轴承滚道表面。裂纹扩展时期的循环次数占总循环次数的76.30%。相比摩擦因数为0.05情况，摩擦因数增大到0.15后裂纹萌生位置距离表面更近，且裂纹扩展到表面时夹杂物右侧的裂纹明显更多，这是由于接触区摩擦力指向右。裂纹萌生寿命和扩展寿命都相对减小且裂纹扩展寿命占总寿命的百分比略有减小。

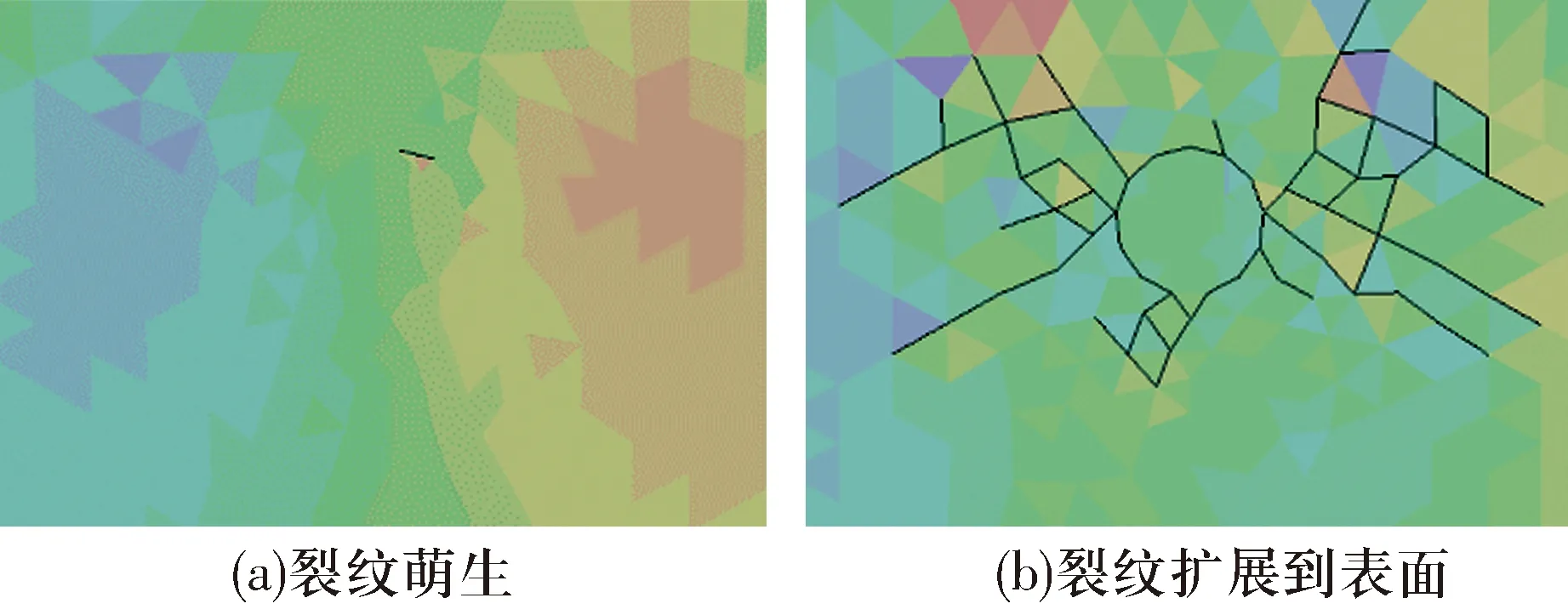
图8 更大摩擦因数下疲劳裂纹的萌生与扩展(fμ=0.15)

4 结论

建立了一种结合连续损伤力学的内聚力模型，用于模拟滚动接触循环加载下夹杂物周围的裂纹萌生与扩展，得出以下结论：

1)该模型可以模拟含夹杂物轴承次表层裂纹从萌生至扩展到接触面的过程，裂纹萌生位置为夹杂物周围，初始寿命Nin为3.23×106，总寿命Nfail为17.92×106,裂纹扩展时期的循环次数占总循环次数的81.97%。

2)在载荷较低的高周循环中，裂纹首先萌生在夹杂物周围，滚动接触的疲劳裂纹扩展阶段平均寿命占总寿命的比例较大。在较大的接触载荷作用下，裂纹萌生位置与扩展方式没有太大变化，但裂纹扩展寿命占总寿命的百分比明显减小。

3)增大接触区的摩擦因数，裂纹萌生位置更接近接触区表面及夹杂物右侧，即摩擦力方向的裂纹数量明显增多。裂纹萌生寿命和扩展寿命都相对减小且裂纹扩展寿命占总寿命的百分比略有减小。