考虑土体剪胀性的盾构倾斜隧道开挖面稳定性分析
胡阿平,孙望成,2,尹华东,朱远嫘,蒋 瑾
(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201;2.中铁五局集团第一工程有限责任公司,湖南 长沙 410117)
0 引 言
随着盾构施工技术逐渐完善,该方法在地铁隧道施工中得到广泛应用。在盾构隧道掘进中,保证掌子面的稳定性是盾构施工技术的关键问题。对隧道稳定性进行分析时,极限分析法由于计算简便、结果精确等优点得到广泛应用[1-3]。基于线性Mohr-Coulomb破坏准则,张翔等[4]通过构建隧道底部隆起的破坏模型,计算出浅埋隧道的围岩压力,并与实际工程数据对比,验证了该方法的有效性;贺志军等[5]综合考虑掘进深度和地表倾斜的影响,采用上限法得出了浅埋隧道的围岩压力;梁桥等[6]考虑土体非均质的特性,结合上限法,得到了土质隧道掌子面的极限支护力;黄阜等[7]采用极限分析上限法和空间离散技术,计算出了孔隙水作用下隧道掌子面最优上限解。然而,土体通常呈现非线性破坏。因此,一些学者考虑土体非线性破坏准则对隧道稳定性进行研究。于丽等[8]基于非线性破坏准则,通过构建的三维塌落破坏模式,分析了孔压效应下浅埋隧道的塌落范围和极限支护力;李得建等[9]将圆锥截交线公式引入三维被动圆锥破坏机制中,并基于非线性破坏准则,分析了超载作用下隧道开挖面的稳定性。罗伟等[10]采用非线性破坏准则,通过构建的斜坡地段隧道破坏机制,计算出坡顶荷载作用下隧道的围岩压力。
以上研究均假定土体服从关联流动法则,但是研究表明[11-12]土体材料通常服从非关联流动法则,关联流动法则仅是其中一个特例。安永林等[13]运用有限元分析法,研究隧道掌子面的稳定性,发现隧道倾角对掌子面稳定性有一定影响。在实际工程中,盾构隧道一般均存在倾角。因此,本文基于非线性Mohr-Coulomb破坏准则,在考虑土体的剪胀效应下,采用极限分析上限法求解了盾构倾斜隧道掌子面上所需的最优支护力,得到了掌子面的潜在破坏面。
1 基本定理
1.1 上限定理
极限分析上限定理表明:在一个相容的运动许可速度场中,材料处于极限荷载状态时,变形机构所承受的表面力和体积力必然不小于材料所承受的真实的破坏荷载。相关表达式为[14]:
(1)
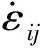
1.2 非线性Mohr-Coulomb破坏准则
研究表明[15-16]土体发生破坏时通常表现为非线性破坏。针对隧道稳定性进行分析时,考虑土体为非线性更加接近工程实际。非线性M-C破坏准则表达式为
τ=c0(1+σn/σt)1/m
(2)
式中:c0为初始粘聚力;σt为轴向抗拉强度;τ和σn分别为剪应力和正应力;m为非线性系数。
1.3 非关联流动法则
传统塑性理论假设土体材料产生变形时遵守关联流动法则。然而,对于土体的剪胀问题,使其遵守关联流动法则时,土体产生的剪胀值与实际值偏差较大。研究表明[17-18]土体材料通常遵守非关联流动法则。因此,修正后的初始粘聚力c0为
τ=ηc0(1+σn/σt)1/m
(3)
式中:η为剪胀系数。
相应的切线方程为
(4)
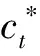
联立式(2)和式(3),此时土体的剪切强度参数之间关系为[17-18]
(5)
2 计算模型
本文根据已有文献[19-20]构建了盾构倾斜隧道开挖面破坏模式,如图1所示,由隧道开挖面AB和两条对数螺旋线AE、BE组成破坏体AEB,其中两条对数螺旋曲线交点E的夹角为2φ。在开挖面破坏时,破坏体AEB以角速度ω绕O点发生旋转破坏。H为隧道埋深,C和β分别为隧道的洞径和倾角,土体重度为γ,rOA=OA,rOB=OB。对数螺旋曲线AE、BE以及相应几何关系如下
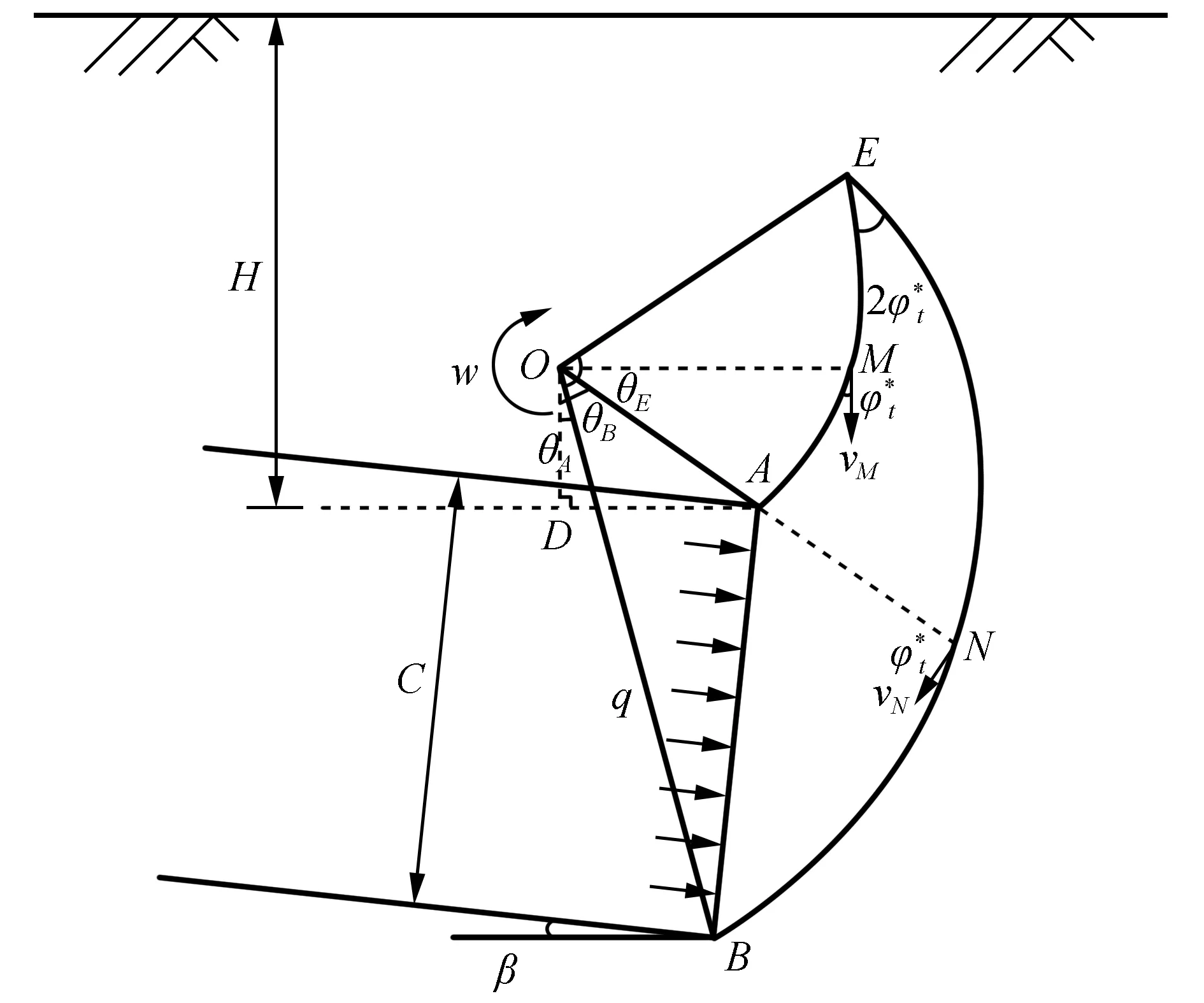
图1 盾构倾斜隧道开挖面破坏模式Fig.1 Failure mode of the excavation surface of the shield inclined tunnel
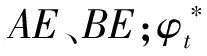
3 计算过程
3.1 外力功率
本文研究的外力为支护力和土体自重。在图1中,考虑土体重力作用,将破坏体ABE划分为AEN和BAN两部分做功,分别记为Pγ1和Pγ2。土体重力总功率为
(11)
式中:
假定支护力q均匀分布在掌子面上,则支护力功率PT表达式为
(16)
3.2 内能耗散率
土体内部能量损耗发生在速度间断线AE和BE上,分别表示为PV1和PV2。总内能耗散率为
(17)
式中:
(18)
(19)
3.3 上限解
令外功率等于内能耗散,即Pγ-PT=PV,求得支护力q的解析表达式:
(20)
(21)
基于Matlab软件中序列二次算法,使式(20)在式(21)约束下求解出隧道掌子面支护力的最优上限解。
4 结果分析
4.1 对比分析
文献[11]基于非关联流动法则,采用上限法计算出盾构隧道掌子面所需支护反力。本文令隧道倾角β=0,即不考虑倾角的影响,与之进行对比。参数按照文献[11]取值:C=8 m,γ=18 kN/m3,σt=30 kPa,h=30 m,c0=10 kPa,m=1.2,η=0.8。
如表1所示,在不考虑隧道倾角(β=0°)时,求得极限支护力为84.8 kPa,与文献[11]中计算值85.6 kPa比较,相对误差为0.9%,验证了本文方法的正确性和有效性。考虑隧道倾角的影响,令β=0°与β=8°进行比较,支护力相对误差为7.6%。考虑土体剪胀效应,取隧道倾角β=0°,令η=0.6与η=1.0进行比较,支护力相对误差为61.1%。由上可知,隧道倾角β和土体剪胀系数η对隧道开挖面支护力均有不同程度的影响,其中土体剪胀系数η影响尤为显著。
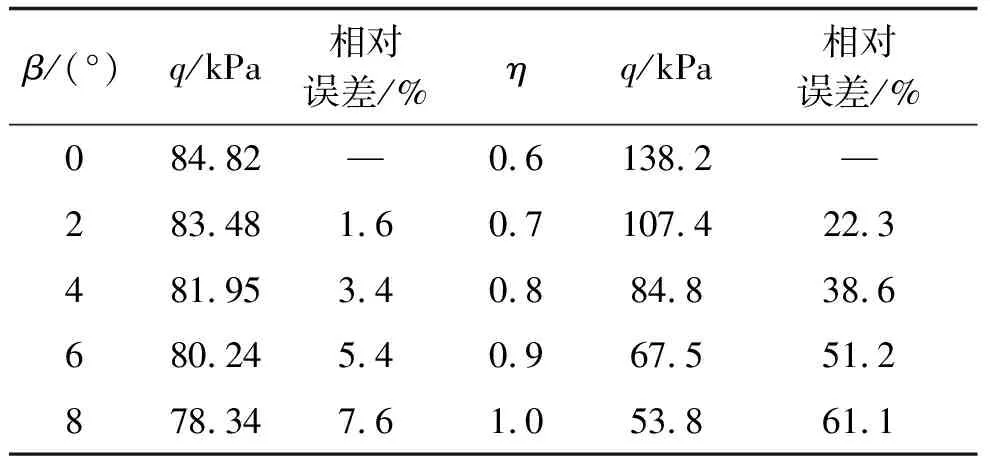
表1 结果对比Table 1 Comparison of results
4.2 各参数对极限支护力的影响
在考虑土体剪胀效应的盾构倾斜隧道稳定性分析中,研究非线性系数m、剪胀系数η、隧道倾角β、隧道洞径C、土体重度γ、初始粘聚力c0以及轴向抗拉强度σt对开挖面支护力q的影响。选取参数取值如下:隧道洞径C=8~10 m,隧道埋深h=30 m,土体重度γ=18~22 kN/m3,轴向抗拉强度σt=20~40 kPa,非线性系数m=1.1~1.5,剪胀系数η=0.6~1.0。
在图2(a)中可以看到,随着初始粘聚力c0逐渐增大,支护力q表现为减小的趋势;而随着非线性系数m逐渐增大,支护力q表现为增大的趋势。以m=1.3为例,求得c0=10 kPa与c0=18 kPa的支护力分别为167.1 kPa和49.2 kPa,相对误差为70.6%。当c0=10 kPa时,求得m=1.1与m=1.5的支护力分别为109.3 kPa和242.0 kPa,相对误差为121.4%;这表明,土体粘聚力c0越大对支护力的减小效应越显著;非线性系数m越大对支护力的增大效应越显著。在图2(b)中能看出,当剪胀系数η增大时,支护力q减小。以m=1.3为例,分别取剪胀系数η=0.6、η=0.8与η=1.0进行比较,支护力相对误差分别为57.5%、36.7%。由此可见,土体剪胀效应对支护力q的影响较为明显,在土体剪胀系数较小时,应加强盾构倾斜隧道开挖面的支护力度。在图2(c)中,随着轴向抗拉强度σt和土体重度γ逐渐增大,支护力q表现为增大的趋势。当土体重度γ=20 kN/m3时,轴向抗拉强度由20 kPa增加到40 kPa,支护力q由104.2 kPa增加到228.4 kPa,相对差值为119.2%。当轴向抗拉强度σt=30 kPa时,土体重度γ由18 kN/m3增加到22 kN/m3,支护力q由141.3 kPa增加到193.7 kPa,相对差值为37.0%。这表明轴向抗拉强度σt和土体重度γ均对支护力有明显的提高效应。在图2(d)中,随着隧道洞径C增大,支护力q增大;随着隧道倾角β逐渐增大,支护力q减小。以隧道倾角β=4°为例,隧道洞径C由6 m增加到10 m,支护力q由70.5 kPa增加到168.6 kPa,相对差值为139.0%。当隧道洞径C=8 m,隧道倾角β由0°增加到8°,支护力q由121.6 kPa减小到112.7 kPa,相对误差为7.3%。这说明,隧道洞径C大小的变化对支护力q影响较大,而隧道倾角β在小幅度变化时对支护力q影响较小。
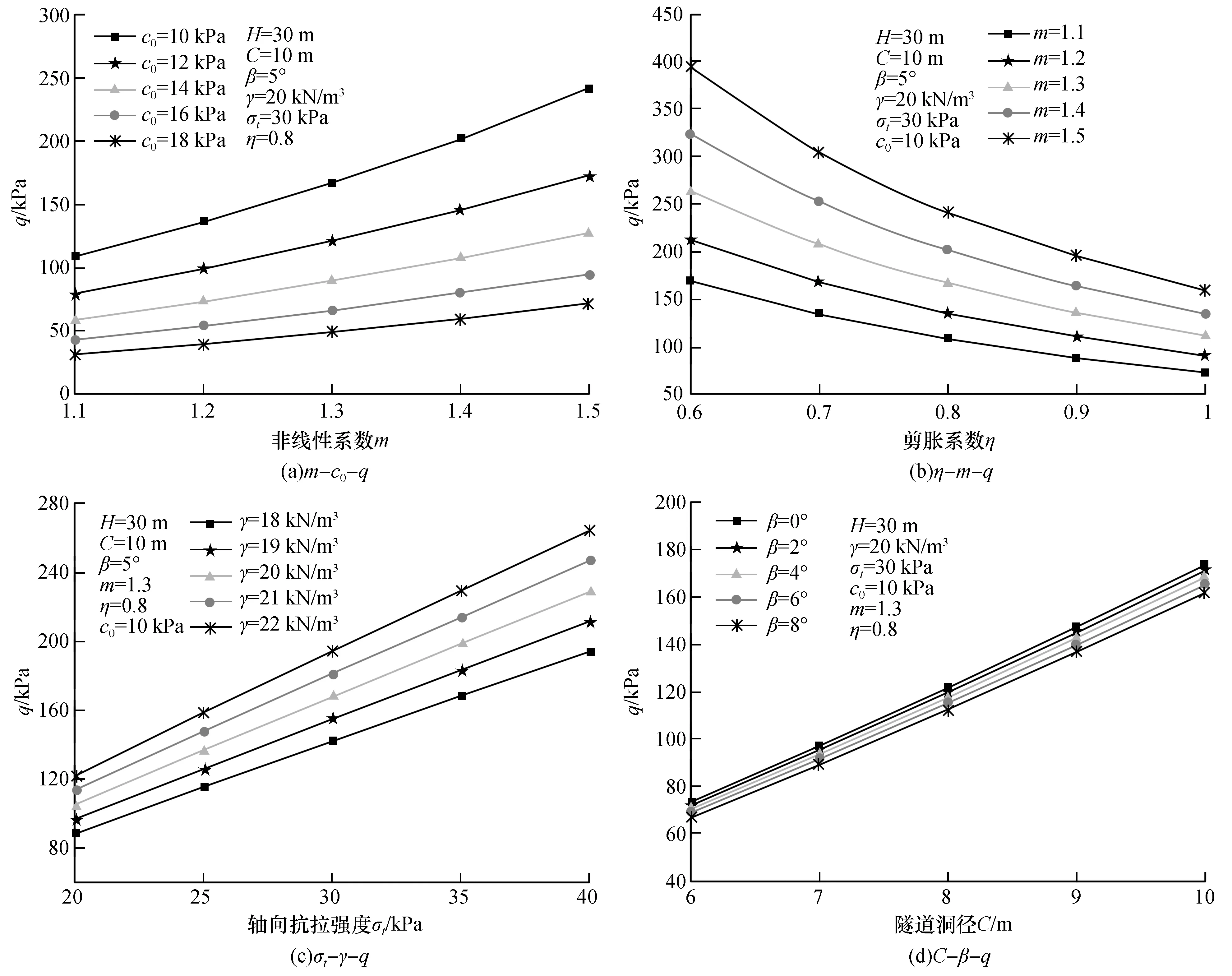
图2 各参数对支护力的影响Fig.2 The influence of various parameters on supporting force
4.3 各参数对破坏面的影响
图3反映了隧道倾角β、非线性系数m、剪胀系数η、初始粘聚力c0以及轴向抗拉强度σt对隧道掌子面破坏面的影响。从图3(a)中可以看出,随着β逐渐增大,破坏范围变化不大,破坏面位置向开挖方向延伸,破坏面顶角主要向开挖方向发展;在图3(b)和(e)中,随着m和σt逐渐增大,破坏范围显著增大,破坏面位置向开挖方向延伸,破坏面顶角主要向隧道上方发展;在图3(c)和(d)中,随着η和c0增大,破坏范围明显减小,破坏面位置向掌子面靠近,破坏面顶角主要向隧道方向靠近。以上表明,初始粘聚力c0、隧道倾角β、土体剪胀系数η、轴向抗拉强度σt以及非线性系数m均对破坏面有明显影响。在实际工程中,进行锚杆支护时,可根据破裂角的变化来确定锚杆支护的长度和角度。因此,隧道倾角β改变时需及时调整锚杆的支护角度,非线性系数m、土体剪胀系数η、初始粘聚力c0和轴向抗拉强度σt变化时需及时调整锚杆的支护长度,充分发挥锚杆在盾构倾斜隧道中的支护作用。
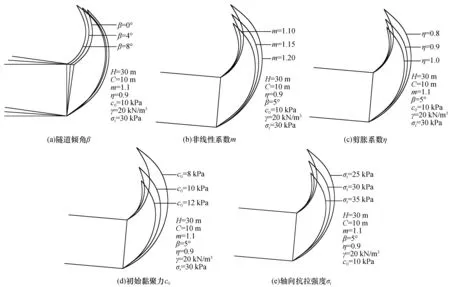
图3 各参数对破裂范围的影响Fig.3 The influence of various parameters on the rupture range
5 结 论
1)不考虑隧道倾角(β=0°)时,采用本文方法求解的支护力与文献计算值高度吻合,验证了本文方法的正确性和有效性。同时,对比发现剪胀系数η对支护力的影响程度大于隧道倾角β。
2)当隧道洞径C、非线性系数m、土体重度γ和轴向抗拉强度σt逐渐增大时,支护力q也随之增大。而随着隧道倾角β、初始粘聚力c0以及剪胀系数η增大时,支护力q减小。当m=1.3时,取η=0.6与η=1.0(关联流动法则)进行比较,支护力q相对误差达到57.5%;当c0=10 kPa时,取m=1.1与m=1.5进行比较,支护力q相对误差达到121.4%;当C=8 m时,取β=0°与β=8°进行比较,支护力相对误差为7.3%。因此,如果忽略非线性系数m和剪胀系数η的影响,求得盾构倾斜隧道开挖面的支护力会存在明显误差。
3)当隧道倾角β增大时,破坏范围变化较小,破坏面位置向开挖方向扩展,破坏面顶角主要向开挖方向发展;当非线性系数m和轴向抗拉强度σt增大时,破坏范围显著增大,破坏面位置向开挖方向扩展,破坏面顶角主要向隧道上方发展;当剪胀系数η和初始粘聚力c0增大时,破坏范围减小,破坏面位置向掌子面靠近,破坏面顶角主要向隧道方向靠近。

