十二股二维编织PBO 绳索结构强度仿真分析

王 哲,赵海涛,刘 扬,陈吉安

（上海交通大学 航空航天学院,上海 200240）

航空航天等高端领域对二维编织绳索的需求越来越迫切，使得二维编织绳索的应用得到迅速的发展。二维编织技术是一种通过沿织物成形方向取向的多根纤维束按照特定的规律倾斜交叉使纤维束交织在一起形成编织物的工艺[1]。通过传统的设计方法研制二维编织绳索成本比较高，随着有限元仿真技术的成熟，利用有限元仿真方法研究二维编织绳索的力学性能越来越受到学术界的青睐。

目前国内外有许多学者对聚对苯并噁唑（PBO）纤维展开了研。赵婷玉等采用射线辐照的方法研究了PBO 纤维增强有机硅压敏胶的性能，结果表明，辐照原位改性可以提升压敏胶的耐热性和高低温力学性能[2]。冉茂强等探讨了PBO 纤维拉伸性能测试的影响因素，得到了测试PBO 纤维拉伸性能的最佳条件，并在最佳条件下测定了其拉伸强度等性能参数[3]。刘姝瑞等进行了PBO 纤维性能研究，测定了纤维的紫外性能等多项性能，并观察了处理前后纤维表面形态的变化[4]。Zhang 等从PBO 纤维分布方面对纤维束强度进行了研究，假设单根纤维强度的分布函数符合矩形分布或正态分布，预测了纤维束的断裂过程，还利用威布尔分布对PBO 纤维束的断裂过程进行了预测，并与矩形分布和正态分布进行了比较[5]。

计算机有限元分析的应用推动了二维编织绳索的研究。马晓红等介绍了编织角及编织结构的变化对复合材料各种性能的影响、建模方法和二维编织成型原理、纤维在复合材料中的取向以及建立的实体模型仿真分析[6]。王奇志等通过有限元仿真的方法，对二维编织陶瓷基复合材料的偏轴拉伸力学性能进行了预测，提出了一种有效的数值模拟方法[7]。Gu 等通过对不同编织角的二维编织碳环氧复合管状绳索进行了渐进式全场变形仿真分析，研究绳索的扭转渐进损伤和失效机理，得出45°的编织角更有利于提高结构的扭转性能[8]。Miao 等提出了一种确定织物微观几何形状模型的静态松弛方法，模拟了二维编织过程，采用该方法生成了二维编织织物，并且该方法能够节省大量的计算资源[9]。

丁许等研究了编织角对芳纶纤维编织绳索拉伸性能的影响，发现编织角逐渐增大时纱线在编织绳索轴向的应力分量逐渐减小[10]。马晓红等对8 种不同工艺参数的碳纤维管状编织绳索进行研究，得出编织节距减小会加重纤维束磨损而出现织物表面的起毛现象[11]。Xu 等通过实验的方法对尼龙、聚酯、高模量聚乙烯的非线性力学特性进行了模型实验研究，采用扩展卡尔曼滤波器准确估计了系统绳索动态刚度的经验表达式参数[12]。魏雅斐等介绍了适用于柔性绳索的不同应变测试方法，总结了电测法和光测法的研究进展[13]。韩雷等通过实验研究了玄武岩纤维二维编织绳索拉伸性能，测得了绳索试件抗拉强度均值[14]。Vu 等采用有限元模拟的方法研究了合成编织绳索力学性能，并进行了拉伸实验的验证，结果表明，摩擦使得纤维束之间的负荷转移，导致应力的不均匀分布[15]。杨超越等对不同节距二维编织绳索进行研究，结果表明，拉伸性能随绳芯节距增加呈现先增大后减小的趋势[16]。

本工作根据十二股二维编织绳索的编织规律，建立不同结径比的十二股二维编织绳索模型，并截取模型的代表性体积单元，施加周期边界条件进行有限元分析，针对不同结径比的绳索进行拉伸实验，探究结径比对绳索强度的影响。

1 十二股绳索编织规律

二维编织机按编织物成形的方向分为竖直式编织机和水平式编织机，竖直式编织机的编织物按竖直方向成形，水平式编织机的编织物按水平方向成形，编织机的携纱器形成一个圆环，有偶数个携纱器，最少8 个，可以以4 的倍数递增。

本工作研究的十二股二维编织绳索采用竖直式编织机，主要由机器底盘、驱动器和携纱器组成，如图1（a）所示，机器底盘上有6 个驱动器，驱动器工作原理见参考文献[17]，驱动器带动携纱器做周期性循环运动，有红色和黄色各6 个携纱器，携纱器带动纤维束进行编织，得到绳索预制件。

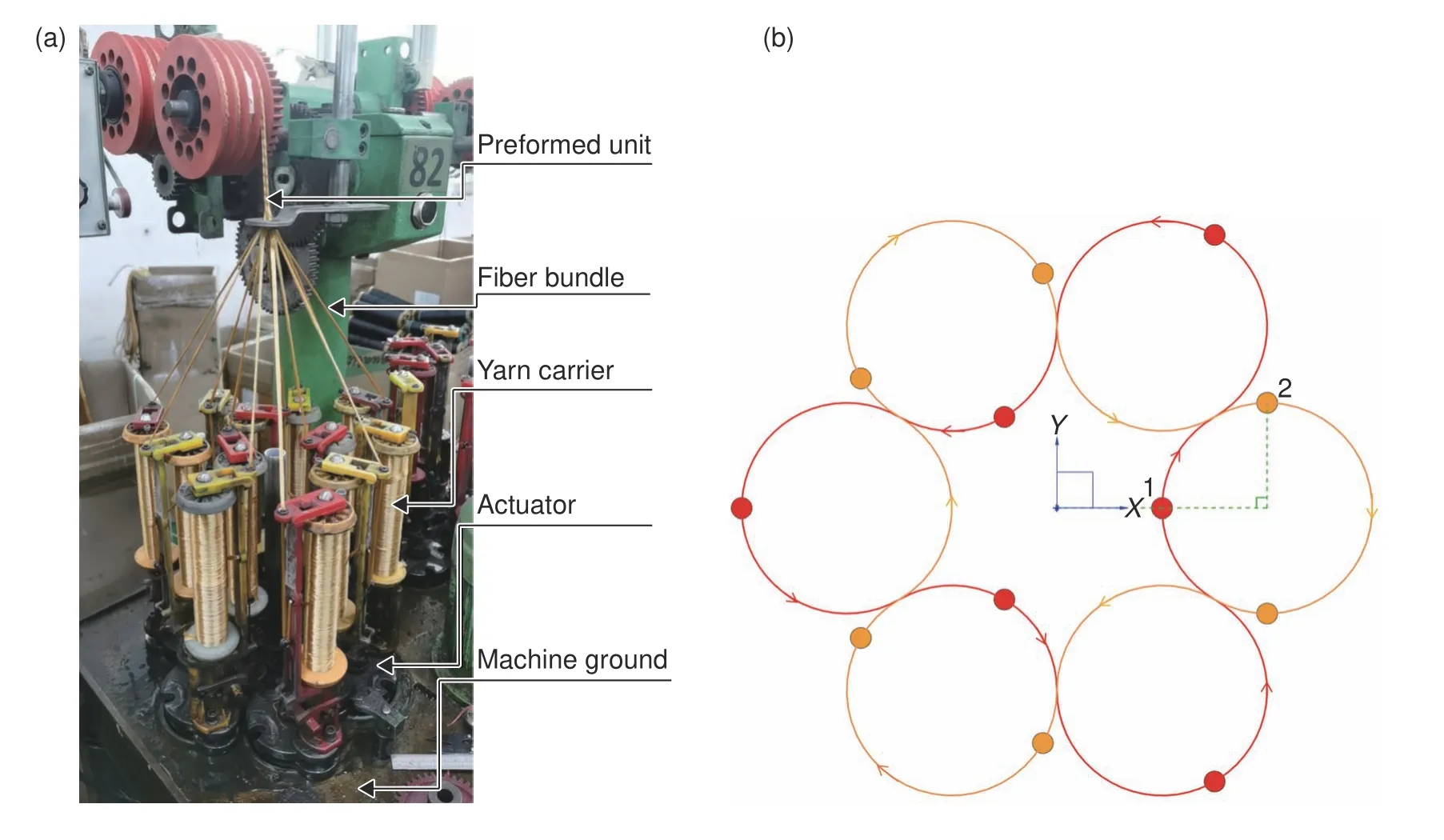
图1 圆形编织机（a）和携纱器运行轨迹（b）Fig.1 Circular knitting machine（a）and yarn carrier running track（b）

携纱器运行轨迹和初始位置的俯视图如图1（b）所示，有2 条运行轨迹，分别用红色和黄色实线表示，组成6 个相切的圆；红色和黄色实心点表示携纱器；携纱器沿着各自对应颜色的轨迹做周期性循环运动，线速度大小相同，箭头表示携纱器的运动方向；以6 个驱动器的对称中心为原点，建立平面直角坐标系，当携纱器1 在x轴上时，携纱器2 与携纱器1 相对所在驱动器中心夹角为90°，其他携纱器的位置可以根据周期性确定，假设某个携纱器沿着轨迹运动一圈回到原始位置视为一个周期，则同一种颜色的携纱器的相邻两个携纱器间隔为1/6 周期。

2 绳索材料和尺寸测量

十二股二维编织PBO 绳索具有优良的性能，绳索的性能主要取决于绳索的结构和所采用的纤维的材料。结构上，此类十二股编织绳索的横截面呈圆形，磨损多发生于绳股端点处，但因其圆形截面，使得磨损不如横截面呈方形的八股编织绳索明显，强度比一般捻制的绳索更高，由于采用两组相反方向纤维束编织而成，使得绳内的力矩平衡，不易发生自旋或者起皱；PBO 纤维是一种高性能有机纤维，具有优良的性能，与其他高性能纤维比较见表1。由表1 可以看出，PBO 纤维的强度、模量和断裂伸长率均最高，密度稍高于芳纶纤维但比碳纤维低，由于其性能优异，所以备受航空航天领域的广泛关注，具有广阔的应用前景[18]。

表1 PBO 纤维与其他高性能纤维的性能比较Table 1 Performance comparison between PBO fiber and other high performance fibers

为建立绳索的二维编织绳索模型，需要测量绳索的外形尺寸，如图2(a)所示，包括花结长度L（绳索最小循环段的长度）和绳索直径d；花结长度L和绳索直径d的比值L/d定义为结径比。

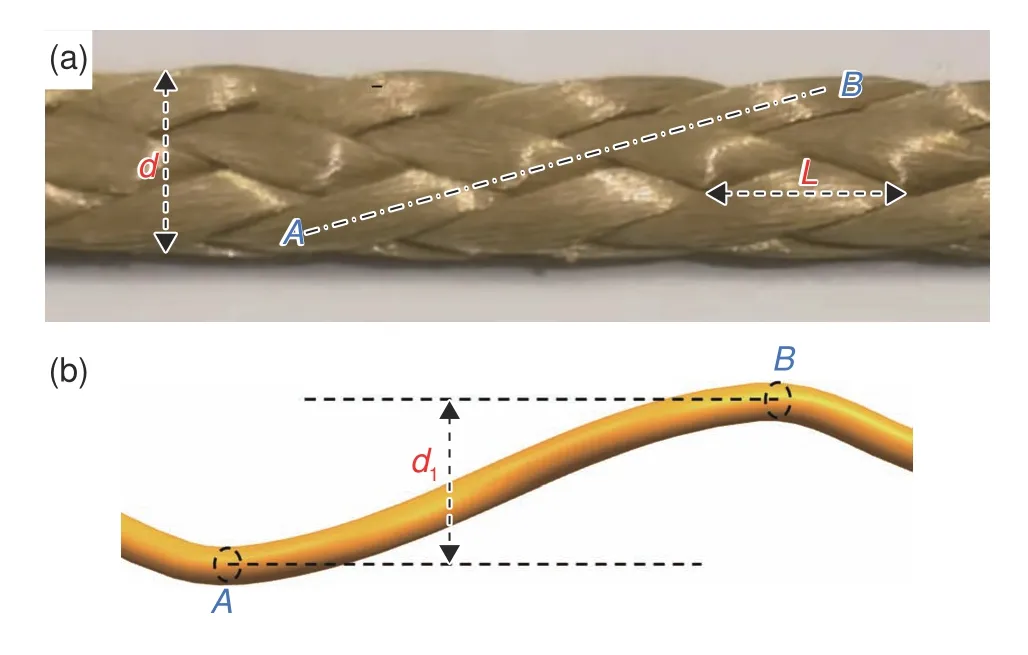
图2 绳索尺寸示意图（a）绳索的外部尺寸；（b）绳索的内部尺寸Fig.2 Schematic diagram of rope dimension（a）external dimension of rope；（b）internal dimension of rope

绳索为直径相同、花结长度不同的绳索。取纤维束AB作为研究对象，如图2（b）所示，纤维束中心线在A、B两点处的切线水平，绳索直径d和两切线之间的距离d1、纤维束半径r的关系为：

实际编织相同直径、不同结径比的绳索时，通过调节编织机和工艺可以使d1相同，采用同一批次的纤维束则可以保证纤维束半径r相同，只要d1和纤维束半径r均相同，根据式（1）即可编织出直径d相同的绳索。

选取5 种直径相同、结径比不同的十二股二维编织PBO 绳索作为研究对象，如图3 所示,各绳索直径均为d=4 mm，从上到下依次编号为1～5。

图3 不同结径比的绳索Fig.3 Ropes with different knot diameter ratios

各绳索的尺寸测量结果如表2 所示。

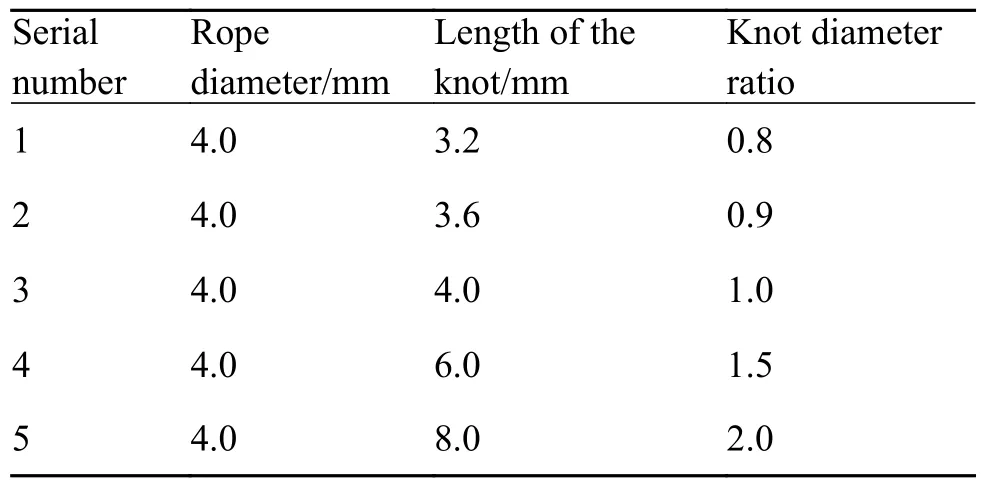
表2 各绳索尺寸测量结果Table 2 Measurement results of each rope size

3 绳索模型的建立

绳索的每股纤维束随着位置的变化成周期性变化，每6 个花结长度为一个周期，在实际绳索6 个花结长度中，等间距切取绳索的横截面确定其中一股纤维束截面的中心位置后，保证模型不重叠且交叉方式与实际一致，得到其中心线的三维轨迹，如图4(a)所示，然后假设纤维束横截面为圆形，扫掠得到如图4(b)所示的一股纤维束的模型，将其平移、旋转后得到绳索模型，如图4(c)所示。

图4 绳索模型建立过程示意图（a）纤维束中心线轨迹；（b）一股纤维束；（c）绳索模型Fig.4 Schematic diagram of rope model building process（a）fiber bundle centerline trajectory；（b）a bundle of fibers；（c）rope model

假设每股纤维束横截面为圆形的依据是：

（1）实际绳索横截面照片如图5（a）所示，从图5（a）可以看出，纤维束斜截面近似为椭圆，因为纤维束与绳索方向有一定的倾斜角度；几何上，如图5（b）所示，圆柱的斜截面近似为椭圆，所以纤维束横截面可以假设为圆形。

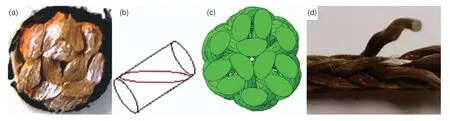
图5 纤维束横截面为圆形的依据（a）绳索横截面；（b）圆柱斜截面；（c）绳索模型横截面；（d）纤维束横截面Fig.5 Basis for round fiber bundle cross section（a）rope cross section；（b）cylindrical oblique section；（c）rope model cross section；（d）fiber bundle cross section

（2）在编织过程中，首先得到的是与实际绳索编织路径一致的绳索预制件，然后经过拉紧工序后得到最终绳索；拉紧工序使纤维束之间相互挤压，横截面会变形，所以可以假设纤维束横截面为圆形建立绳索预制件模型，有限元分析时对绳索预制件模型施加拉伸载荷，纤维束之间会相互挤压，横截面形状会逐渐趋向于与实际一致，如图5（c）所示。

（3）取出一股纤维束，再垂直于纤维束切线方向切，得到纤维束的横截面照片如图5（d）所示，可以看出，纤维束横截面近似为圆形。

为了使模型的体积与实际绳索的体积相同，首先采用量筒排水法测量出实际绳索6 个花结长度的实际体积，以此调整模型的体积，使6 个花结长度的绳索模型的体积与实际相符。

4 周期性边界条件的施加和材料损伤本构

4.1 RVE 模型

选取绳索模型一个花结长度作为代表体积性单元（RVE），通过对绳索RVE 上下表面施加周期性边界条件以实现对整股绳索的模拟，边界条件选取一般周期性边界条件[19]，得到结果如图6 所示，其中图6（a）为周期性边界条件施加后的RVE，图6（b）为有限元仿真模拟结果。

图6 代表性体积单元强度有限元分析（a）代表性体积单元；（b）有限元仿真模拟结果Fig.6 Finite element analysis of representative volume element strength（a）representative volume element；（b）finite element simulation results

4.2 周期边界条件

具有相对平行的成对界面的单胞模型中沿着X轴方向相对平行界面的周期性位移场如式（2）所示：

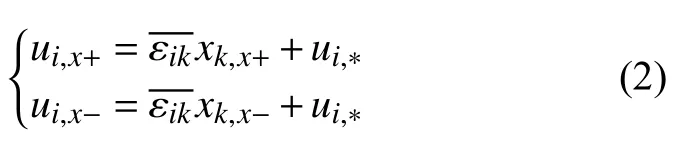
式中：上标x+和x−表示沿着X轴的正轴方向及负轴方向；ui,∗在周期性单胞模型相对面上相等，式（2）中两式相减得到：

式中：xk,x表示沿着X轴平行相对面的间距，对于一个周期结构xk,x是常数，当给定了平均应变载荷后，等式右侧为常数值，即两个相对平行的表面位移差为常数值，因此扩展到其他方向可以写成：

式（4）可以通过ABAQUS 中的多点约束（multi-point constrains，MPC）来实现，相邻RVE 之间可以满足应力连续和位移连续条件；本节研究的绳索是非常见的立方体单胞，其只在Y方向阵列，因此只需要在Y方向的对应平行面上施加周期边界条件即可，对于立方体的规则RVE 结构可以划分周期性网格，同时基本保证对应平行相对面的节点一一对应，本工作研究的绳索结构由于其螺旋的特殊结构无法保证对应面节点一一对应，这就导致了常用的周期性边界条件无法满足要求，因此采用一般周期性边界条件。

4.3 一般周期性边界条件

由于结构的复杂性，显然不适用周期性的网格划分，非周期性的网格将直接导致主平面单元的某个节点M位移到对应面的某个单元内，通过与包含节点M投影的单元节点位移插值，节点M的位移可表达为：

式中：矩阵u代表节点M的位移；矩阵N代表对应面上包含节点M的单元形函数；矩阵δ为节点M周围单元的节点位移。

单胞模型的网格选取四面体单元C3D4 进行划分，因此主平面单元节点M周围单元为三角形单元，因此节点M的位移可以表达为：

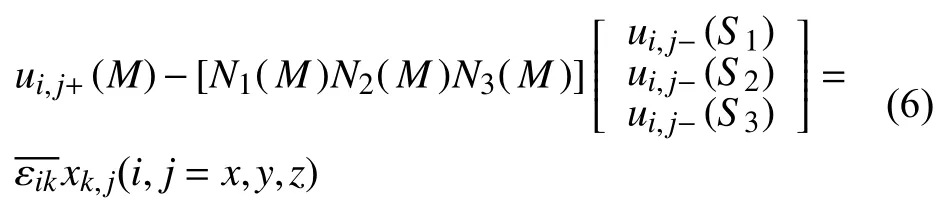
点M所对应的三角形单元的节点表示为Si(i=1,2,3)，位移插值函数为Ni(i=1,2,3)。三角形面积坐标与所处平面直角坐标联系如图7。

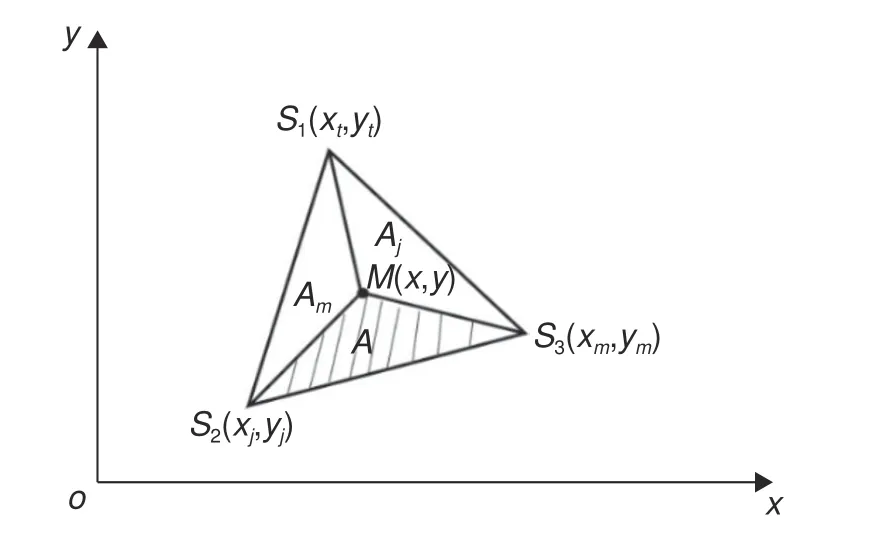
图7 三角形面积坐标与直角坐标之间的关系Fig.7 Relation between triangle area coordinates and cartesian coordinates

其中，S1(xi,yi),S2(xj,yj),S3(xm,ym)表示在直角坐标系中三角形单元顶点的位置，M(x,y)表示在直角坐标系中主平面单元节点M的位置，则△S1S2S3、△S2S3M、△S1S3M及△S1S2M面积A、Ai、Am、Aj在直角坐标系中可表示为：

其中

则面积坐标表达式为：

三角形单元的位移插值函数在面积坐标中可表示为：

4.4 材料本构模型

由于存在明显的塑性断裂过程，采用弹塑性延性损伤本构理论，塑性硬化采用各向同性硬化，采用ABAQUS 自带的延性损伤准则判断材料的损伤起始、扩展以及完全破坏。图8 为材料在延性损伤准则下的应力-应变关系。

如图8 所示，当材料损伤曲线上出现明显屈服应力软化和弹性退化时，表示出现了材料损伤，材料损伤由损伤变量D描述。断裂能Gf表示如式（12）：

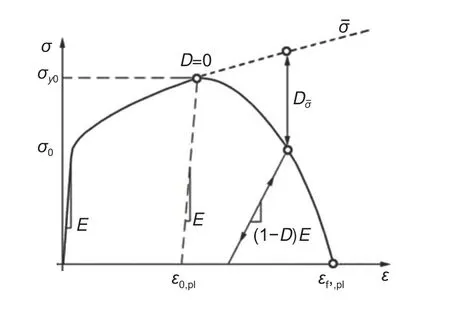
图8 材料损伤累积应力-应变关系曲线Fig.8 Cumulative stress-strain relationship curve of material damage

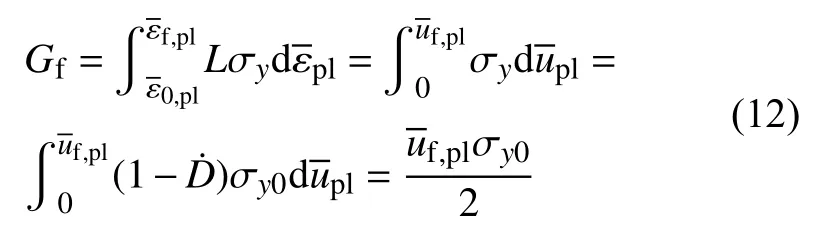
式中：L为单元特征长度，与单元网格尺寸有关；定义为材料完全损伤时的塑性位移。和分别表示损伤变量D为0（材料初始破坏）和1（材料完全破坏）时的等效塑性应变。σy0为材料的应力承载达到最大值时的屈服应力。其中，等效塑性位移经式（11）简化得：

5 绳索强度影响因素的有限元数值分析与实验

图9 为绳索局部示意图。绳索受到拉力时，纤维束C 受到相邻两个纤维束A、B 的挤压力，其大小相等、方向相反、作用线相隔很近，两挤压力作用的截面沿着相反方向发生错动，从而使纤维束C 发生剪切变形。由于绳索是周期性循环，且高度对称结构，所以每股纤维束都受到相邻纤维束的挤压力而形成剪切力，而拉力和剪切力大小影响绳索的强度且与绳索结构有关，绳索结构又由结径比决定，结径比越大相邻纤维束之间的夹角θ越小。

图9 绳索局部放大示意图Fig.9 Schematic diagram of partial enlargement of rope

因为绳索结构和纤维束之间的挤压力即接触面均非常复杂，本节运用第4 节的理论，对纤维直径相同、结径比不同的绳索模型进行有限元仿真分析，探究结径比与绳索强度的关系。

5.1 结径比对绳索强度的影响

绳索直径一定时，花结长度越小则结径比越小；图10（a）为纤维束直径相同、结径比依次增大的绳索模型，本节通过对该系列绳索模型仿真分析，探究结径比对绳索强度的影响，得到绳索模型能承受的最大拉力的仿真结果如表3 和图10（b）、（c）所示。

从表3 和图10（c）结果得出，纤维束直径相同时，随着结径比的增大，绳索能承受的最大拉力先增大后基本不变，因为绳索的结径比较小时，更偏向于因纤维束之间的挤压力而剪断，因为纤维的剪切强度远小于其拉伸强度，所以绳索能承受的最大拉力随着结径比的增大而先增大，当结径比增大到1.0 左右时，再继续增大结径比，纤维束之间的挤压力减弱，绳索更偏向于被拉断，因为纤维束直径相同，所以绳索能承受的最大拉力先基本不变。本工作编织方法得到的十二股二维编织绳索有特定的临界结径比[N] 值，假设绳索模型结径比用N表示，那么，如果N＜[N]，则更容易被纤维束之间的挤压力剪断；如果N=[N]，则绳索是处在被拉断和纤维束之间的挤压力剪断临界点；如果N＞[N]，则该材料的绳索受拉时更偏向于被拉断，即纤维编织而成的绳索存在一个特定的结径比，在该节径比下绳索破坏模式发生转变。

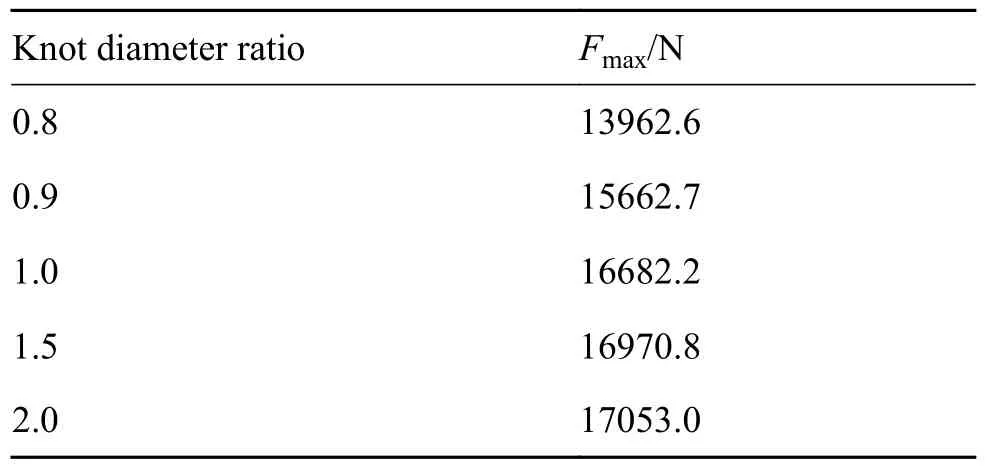
表3 不同花结长度的绳索模型能承受的最大拉力Table 3 Maximum tensile strength of rope models with different knot lengths

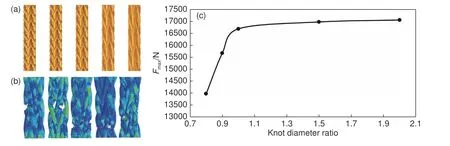
图10 绳索模型及其有限元分析结果（a）纤维束直径相同、结径比依次增大的绳索模型；（b）仿真结果；（c）绳索模型能承受的最大拉力Fig.10 Rope model and its finite element analysis results（a）rope model with the same fiber bundle diameter and increasing knot diameter ratio；（b）simulation results；（c）maximum tensile force that the rope model can bear

5.2 不同结径比的绳索拉伸实验

实验仪器采用SUNS 单轴拉伸试验机及缠绕式夹具，将绳索的下端固定不动，上端与拉伸机夹具连接随夹具向上运动，受到的拉力逐渐增大，直到拉断，拉伸机实时记录此拉力的变化过程。

通过对第2 节中不同结径比的绳索进行拉伸实验，每种结径比的绳索做3 次实验，得到绳索承受的最大拉力，然后分别求平均值，实验结果如表4 所示。

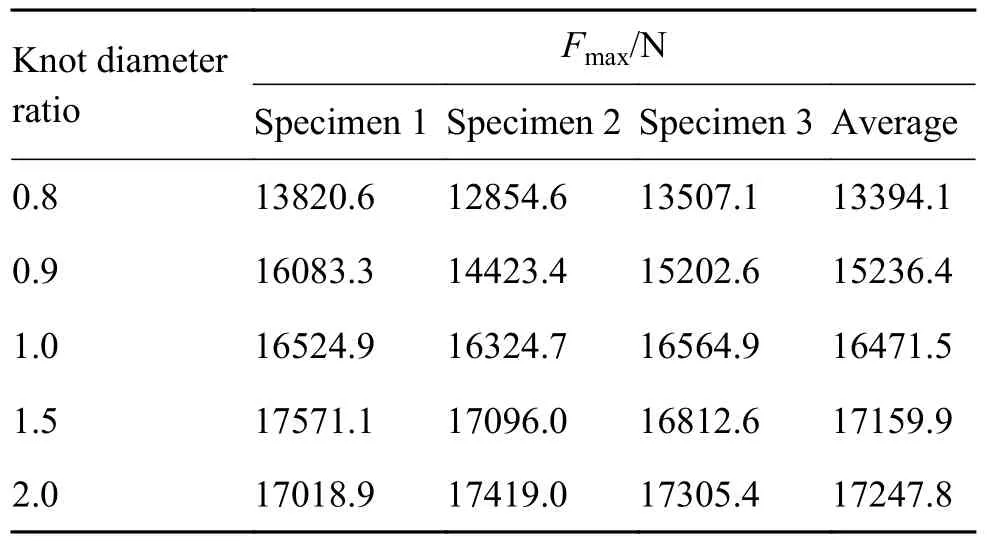
表4 绳索的拉伸实验结果Table 4 Tensile test results of rope

各试件能够承受的最大拉力实验值的平均值与模拟结果对比，如图11 所示，可以看出，实验结果与模拟结果一致：随着结径比增大，绳索能够承受的最大拉力先显著增大后基本不变。

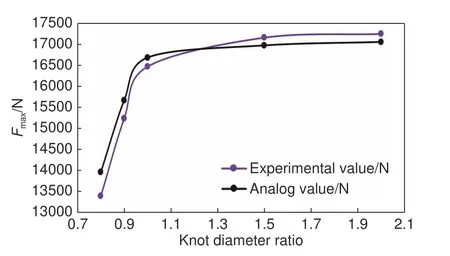
图11 模拟结果和实验结果对比Fig.11 Comparison between simulation results and experimental results

6 结论

（1）实际十二股编织PBO 绳索在受到拉力时，绳索抗拉性能受拉力和各股纤维束之间挤压力形成剪力两个因素影响。

（2）通过施加周期性边界条件进行有限元模拟，绳索直径一定，当结径比较小时，纤维束之间的挤压力而产生的剪切力为影响绳索强度的主要因素，绳索强度随着结径比的增大而增大；而结径比增大到某一特定值时，再继续增大结径比纤维束之间的挤压力减弱，绳索破坏因素转为被拉断，即绳索存在一个特定的临界结径比，大于该结径比下材料抗拉强度才能充分发挥，但结径比过大的绳索容易松散，适中的结径比更具实用性。

（3）纤维束横截面假设为圆形，不可避免会使模型中存在空隙，实际绳索是紧密结构，而模型建立时已经尽可能紧凑将空隙降到最小，使得模拟值与实验值基本一致，能反映出实际规律。