平面外弯矩作用下T 形圆管节点热点应力分布

袁智深，姚尧，卢微然，舒兴平

（1.中南林业科技大学土木工程学院，湖南长沙 410004；2.浙江树人大学城建学院，浙江杭州 310015；3.湖南大学土木工程学院，湖南长沙 410082）

相贯节点疲劳断裂是钢管结构重要的失效形式之一，疲劳裂纹通常萌生于节点相贯焊缝焊趾处的应力幅极大值点［1］.研究表明，在结构杆件内力作用下，应力沿相贯焊缝环向呈现明显的不均匀分布.当承受轴力Fax、平面内弯矩Mipb和平面外弯矩Mopb三种基本形式内力作用时，应力分布情况也明显不同.因此，受杆件内力形式和节点几何参数的影响，应力幅极大值点的位置不尽相同，可能位于相贯线的冠点、鞍点或其之间任意位置［2］.实际工程中相贯节点往往会承受两种或三种基本荷载共同作用，在这种复杂组合荷载作用下的热点应力极值求解问题尚未完全解决.目前，国际上主要有两种思路来解决这一问题：第一种为简化方法，需建立与基本荷载作用下热点应力极值的相关方程，如线性叠加方程［3］、API 叠加方程［4］和YAO 叠加方程［5］等；第二种为精确方法，需建立热点应力分布方程后取极大值［6］，而详细了解热点应力沿相贯线的分布情况是这一方法建立的基础.国内外展开了大量基本荷载作用下相贯线关键点（如冠点和鞍点）的热点应力研究［7-8］，而对热点应力分布研究相对较少.伦敦大学学院利用有限元分析数据拟合了两套热点应力分布计算公式［9-10］，然而由于有限元模型采用壳单元建立，在某些情况下与试验误差较大［2］，因此，未被规范采纳.目前，国内外规范均未给出热点应力分布的计算方法.

本文以基于试验结果的径向拉伸模型为基础对T 形圆管相贯节点在平面外弯矩作用下的热点应力分布进行有限元参数分析，并根据有限元数据拟合了T 形圆管相贯节点的标准化热点应力分布曲线计算公式，最后，将本文拟合公式、UCL 公式计算结果与试验数据进行对比，以验证本文公式的可靠性，从而为复杂组合荷载作用下的热点应力极值求解问题提供基础.

1 有限元模型的建立及验证

1.1 计算简图

图1 所示为T 形圆管相贯节点的计算简图及其几何参数符号.其中，L、l分别为主管和支管长度；D、d分别为主管和支管外直径；T、t分别为主管和支管壁厚.主管两端为刚接，支管端部施加荷载（轴力Fax、平面内弯矩Mipb或平面外弯矩Mopb），荷载在杆端产生的最大正应力称为名义应力σnm，名义应力可根据材料力学知识获得，对于平面外弯矩Mopb作用下的情况，可按式（1）计算.

图1 T形钢管相贯节点计算简图及几何参数Fig.1 Calculation diagram and geometric parameters of CHS T-joints

式中：W为支管截面模量.

1.2 建模及网格划分方法

在常用的结构分析有限单元中，有壳单元和实体单元，而三维20 结点实体单元是节点疲劳应力分析的推荐单元［11-13］，它是三维8结点实体单元的高阶单元，单元每个结点具有沿坐标系x、y、z轴的3 个平动自由度，如图2 所示.本文的有限元分析均采用SOLID95 实体单元作为分析单元.该单元能够适应不规则的形状，并且不损失精度，具有塑性、蠕变、应力刚化、大变形以及大应变的能力，同样适合解决大应变、大变形的非线性问题［14］.

为了保证网格连续性并获得较高的网格质量，本文考虑薄壁管结构的杆件特点，提出了径向拉伸算法来实现壳单元与实体单元间的转换.图3 展示了采用壳面网格划分、拉伸、焊接的径向拉伸建模流程，该算法利用了法向量拉伸的特点，进行了边界的适应性和内部的均匀性修正，以保证相贯线处相贯单元的连续性和质量，算法的基本原理详见文献［2］.利用该算法建立的T 形相贯节点整体网格模型以及局部焊缝网格如图2 所示，由图2 可看出，整个径向拉伸网格保持了很好的连续性和规则性.

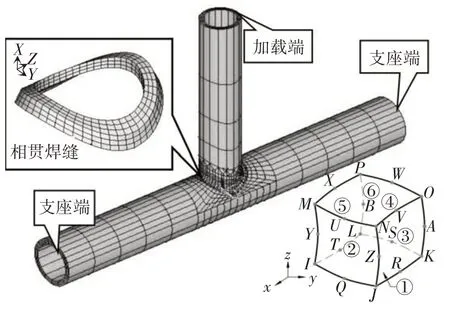
图2 T形节点有限元整体模型Fig.2 Overall model of T-joint for FEA

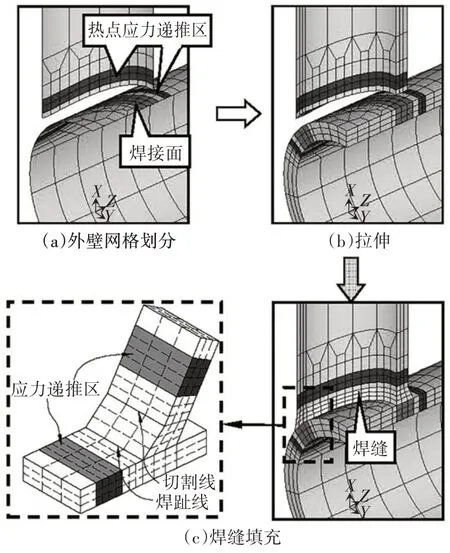
图3 T形节点有限元建模步骤Fig.3 FEA modeling process of T-joint

需要注意的是，相贯焊缝形状对热点应力的影响不容忽视［15］，研究表明，与不考虑焊缝形状的相贯节点相比，相贯焊缝形状可以使热点应力降低5%.本文建立的有限元模型基于这一结论，精确模拟了实际建造时的相贯焊缝形状.

支座和荷载通过杆端单元的端面结点施加.主管端部刚性支座通过约束主管端面所有单元结点的3 个方向的平动自由度（ux、uy、uz）来模拟.支管端部弯矩采用耦合法施加，即将支管端面的所有单元结点通过刚臂耦合于端面的弯矩作用点，作用于刚臂一端的荷载根据刚臂长度分配到相连另一端的各对应端面结点.

1.3 热点应力的获得

受试验测量技术的限制，焊趾位置的应力难以直接测量得到，目前国际焊接协会（IIW）规范以及国际管结构发展与研究委员会（CIDECT）规范均采用焊趾外一定距离点的应力插值作为热点应力σhs［16-17］.试验时通常在垂直焊趾方向排列2～3 个微型单向应变片组成应变片组来捕捉焊趾外的应力，如图4 所示，各应变片到焊趾的距离应满足热点应力递推区间的要求［16］.σhs采用两点应力线性递推至焊趾得出［17］，递推公式如式（2）所示.

图4 应变片组大样Fig.4 Detail of a set of strain gauges

式中：L1、σ1表示近端应变片到焊趾的距离和垂直于焊趾的应力；L2、σ2表示远端应变片到焊趾的距离和垂直于焊趾的应力.

为了清晰地了解热点应力沿相贯线的环向分布情况，在管外壁沿相贯线等间隔布置应力测点，如图5 所示.采用支管圆心角来定位测点，本文选取相贯线冠点为起始点，其对应支管圆心角δ为0°，逆时针方向为正，相贯线鞍点对应的圆心角为90°和270°.

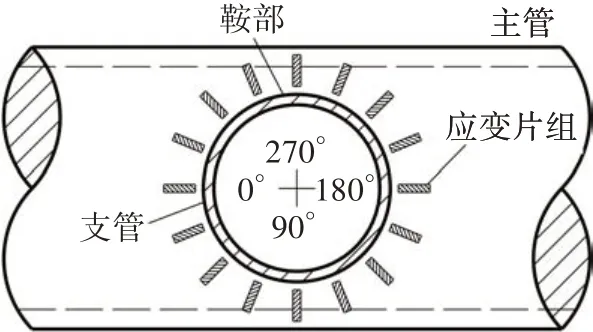
图5 应力测点布置图Fig.5 Layout of stress measuring points

有限元建模时同样采用了与前述规范及试验［16-17］一致的应力测量方式，有限元模型主、支管焊趾外应力递推区设置了额外的沿相贯线环向分布的应力测量网格环，如图3 中应力递推区的网格所示，然后利用外推法获得焊趾处的热点应力.

目前，普遍采用无量纲的应力集中系数SCF 来描述应力集中程度，例如，相贯线上对应支管圆心角δ点的热点应力为σhs（δ），其应力集中系数SCF（δ）可由式（3）表示.

相贯线上应力的不均匀分布本质上是由于相对刚度分布不均所造成的，因此，研究相贯线上的应力分布情况的关键在于相贯线上各点应力的相对关系，本文选择相贯线上某一点作为应力参照点，参照点应力集中系数用符号SCFref表示，并建立其他点应力集中系数SCF（δ）与SCFref的比值曲线，定义为热点应力分布系数DIS：

理论上相贯线任意点均可选为参照点，现有研究对相贯线上关键点的SCF 已经有了非常成熟的认识，因此，本文的参照点选取原则为不受主管长细比影响的关键点，对于平面外弯矩Mopb作用的情况，选择相贯线鞍点的应力集中系数SCFopb，cs为应力分布计算的参照点热点应力，因此，对应的应力分布系数可表示为：

式中：DISopb为Mopb作用下的应力分布系数.

1.4 有限元结果的试验验证

为了检验径向拉伸模型是否能够精确地捕捉节点相贯线处的应力，并在计算精度和计算效率之间达到最佳平衡，本节通过调整网格密度对有限元结果进行了收敛分析.通常网格密度越高，捕捉到的应力可靠性越高.

选取文献［3］中节点试件的几何参数：L=4 130 mm，D=508 mm，d=406.4 mm，T=12.7 mm，t=9.525 mm

为模型参数，对其分别建立了三个不同密度网格模型并对比分析得到的SCF，模型应力递推区沿三个方向（环向×径向×法向）的单元数量如图6 和表1 所示，对应的2#焊缝区分别采用48×3×3、48×1×1 和48×6×6 的网格矩阵，3#焊缝区分别采用48×3×3、48×3×1 和48×3×6 的网格矩阵.不同密度网格模型计算得到的热点应力SCF 如图7 所示.为了检验有限元方法算得的真实应力的精度，本节未将SCF 环向分布曲线转换为应力分布系数DIS曲线的形式.

表1 近焊趾区网格密度Tab.1 Mesh density of region near weld toe

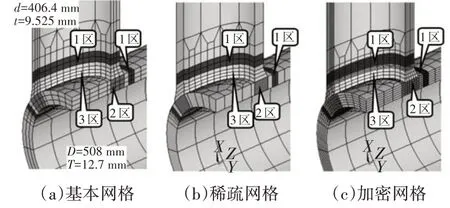
图6 近焊趾区网格密度Fig.6 Mesh density of region near weld toe

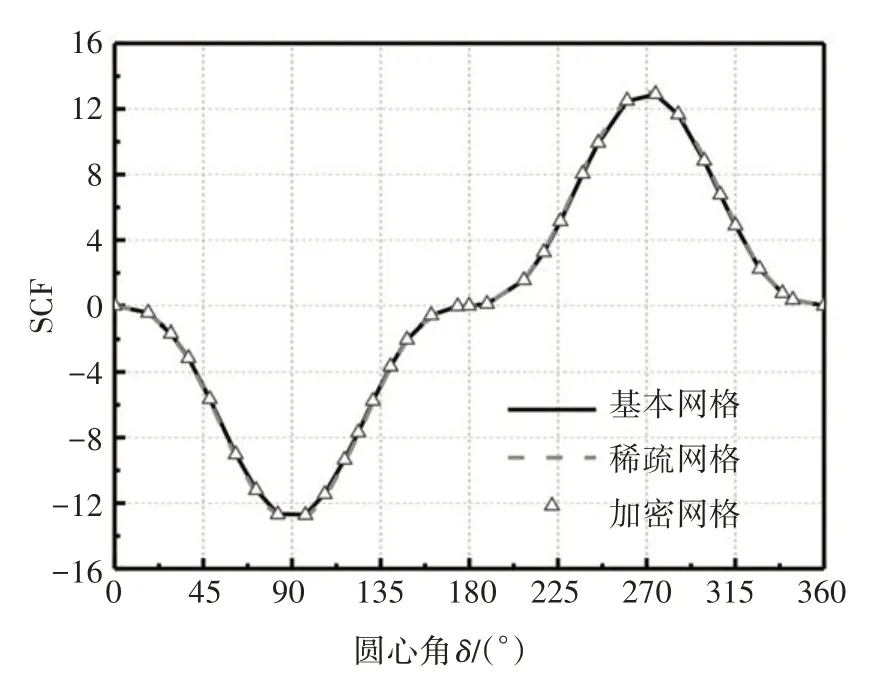
图7 不同密度网格模型SCF环向分布Fig.7 SCF distribution for models of different grid density

对比三组模型的SCF 计算结果可以看出：三组密度网格模型计算结果相差不超过5%，计算结果收敛，稀疏网格模型的计算结果与基本网格、加密网格略有差别，而基本网格和加密网格模型的SCF 环向分布曲线基本重合.由于基本网格模型的网格密度能更好地兼顾计算精度与运算效率的要求，因此，后续分析均采用基本网格.

为了检验有限元计算结果的可靠性，利用上述有限元建模方法对南洋理工大学（NTU）试验［3，18］和伦敦大学学院（UCL）试验［19］中的三组试件进行建模，并与试验结果进行了对比.试件节点参数如表2所示，对比结果如图8 所示.对比表明：有限元计算结果与试验结果吻合良好，验证了上述有限元建模方法的可靠性.

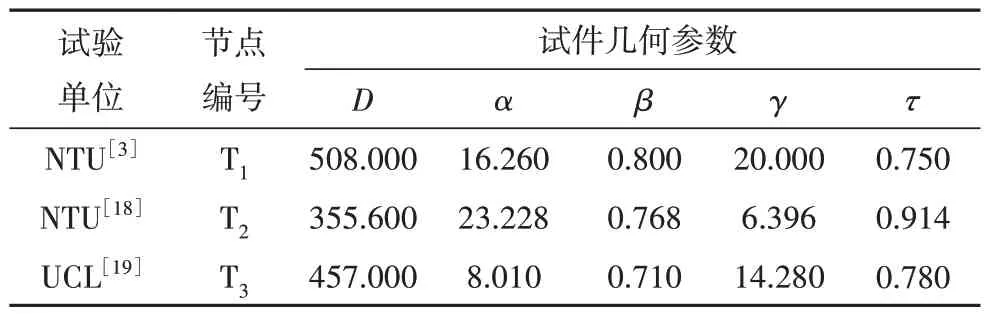
表2 试件节点参数Tab.2 Parameters of DIS test specimens

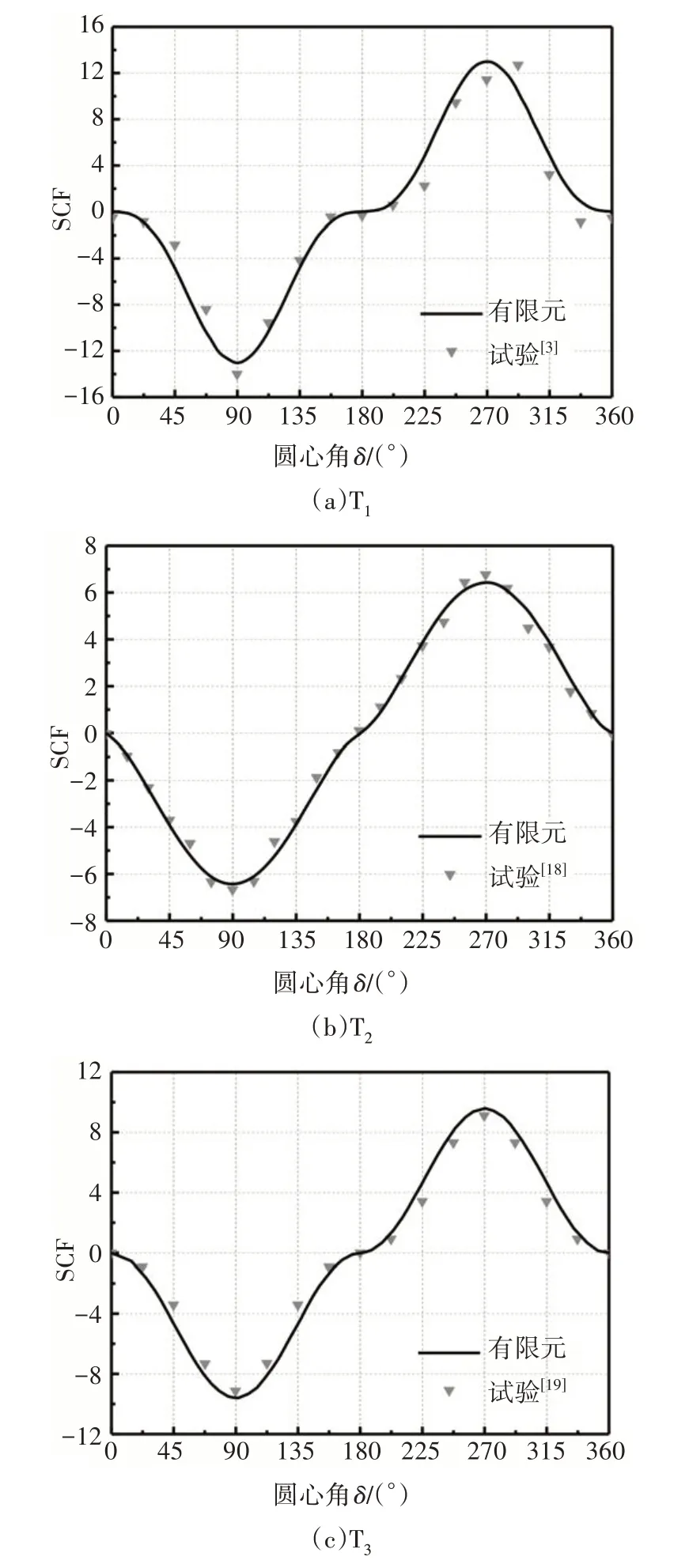
图8 有限元计算结果与试验结果对比Fig.8 Comparison between FEA calculation results and test results

2 参数分析

表3 正交分析的无量纲参数取值Tab.3 Value of dimensionless parameters in orthogonal analysis

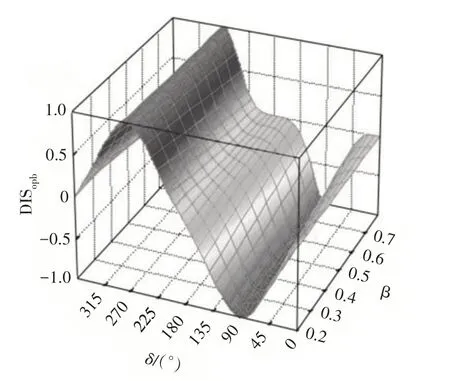
图9 β-DIS曲面Fig.9 β-DIS curved surface

图10 γ-DIS曲面Fig.10 γ-DIS curved surface

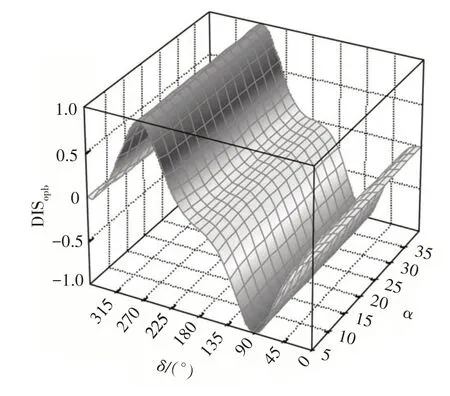
图11 α-DIS曲面Fig.11 α-DIS curved surface

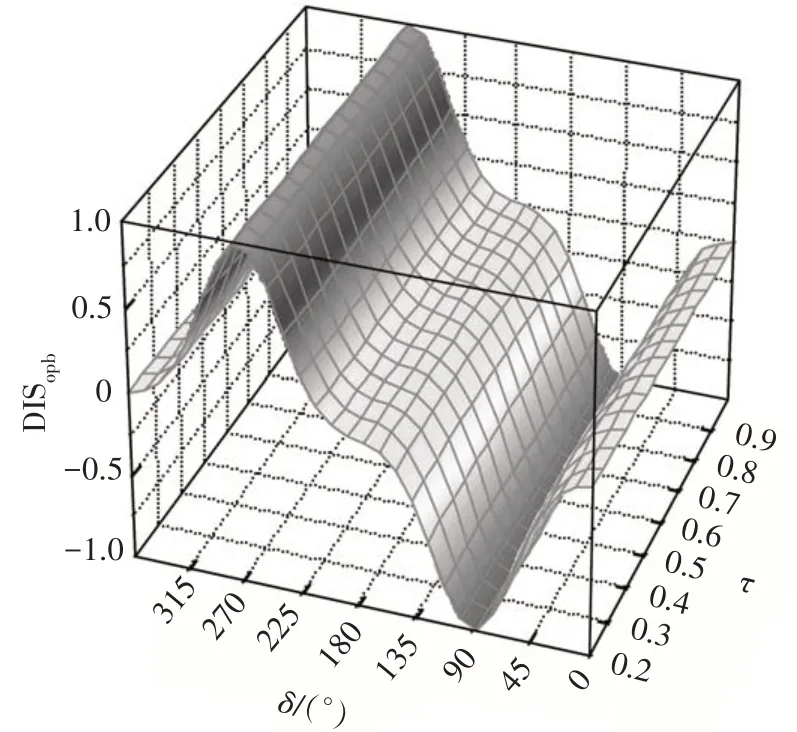
图12 τ-DIS曲面Fig.12 τ-DIS curved surface

2.1 支主管外径比β和主管径厚比γ的影响

图9、图10分别给出了管径比β-DIS和主管径厚比γ-DIS 关系曲面.从图中可看出，平面外弯矩Mopb作用下，DIS分布曲线与其名义应力产生的正弦三角函数分布曲线的整体单调性保持一致，沿相贯线冠点连线（0°-180°连线）反对称，然而，某些情况下，曲线的形状尤其在冠点附近处，与正弦曲线差异明显.

随着β、γ的增大，DISopb曲线冠点位置逐渐出现反弯点，并发展至倾斜的反弯段，当进一步发展至β≥0.6 或γ≥25 时，其反弯段几乎为水平平台段，反弯段宽度逐渐扩展至冠点±30°，鞍点附近的曲线斜率相应变大.

导致这一变化趋势的主要原因是：随着β增加，相贯线鞍点越接近主管侧壁中线，鞍点附近主管的局部刚度增加；而随着γ增加，主管壁厚变小，主管局部刚度减小，但冠点附近减幅更大，两者均导致主管在相贯线鞍点的局部刚度较冠点相对变大，因此，鞍点附近的应力集中增大，而冠点附近应力集中相对减小.

2.2 主管长细比α和支主管壁厚比τ的影响

图11、图12 给出了主管长细比α-DIS 和支主管壁厚比τ-DIS 的关系曲面.由图可以看出，随着α、τ改变，DISopb曲线形状几乎没有改变，其对DISopb的影响可忽略不计.

综上所述，不同几何参数对DIS 曲线形状的影响不同，在4 个无量纲几何参数中，受β、γ的影响较大，而受α、τ影响较小.β、γ改变了DISopb曲线冠点附近的应力分布趋势，当参数大于一定值时，冠点呈现出明显的反弯平台段，平台段宽度达到冠点±30°.

3 参数公式拟合及可靠性分析

3.1 参数公式拟合

DIS 曲线基本满足波浪分布，波幅、周期和冠点平台段是影响曲线形状的关键点，从热点应力分布参数分析结果可以得出DIS 曲线符合以下几个规律：1）Mopb作用下的曲线单调性同正弦三角函数；2）曲线波幅为2，周期为2π；3）冠点比鞍点附近的应力分布更加平缓.

三角函数的指数形式可以同时满足上述原则.如图13所示，当指数大于1时，函数极值点附近的曲线更尖锐，函数值等于0 附近的曲线逐渐趋于平缓，指数越大，平台越宽.根据分布曲线的反弯点平台位置以及周期，假定Mopb的基本函数形式为sinδ，函数周期为2π，显然，基本函数满足应力分布规律，当k≠1 时函数连续且一阶导数连续.在热点应力分布有限元参数分析数据的基础上，拟合了T 形圆管相贯节点在平面外弯矩作用下的热点应力分布系数公式如下：

图13 三角函数曲线Fig.13 Trigonometric function curve

式中：形状修正系数Kopb=|sinδ|k，k=0.109β1.264γ1.662+0.094.

诸多问题的出现严重影响和制约了水景设计的发展.水景一旦形成，应综合考虑长期的实用性，体现景观的生态功能，防止水质恶化[15].如何运用专业技能平衡水景在小尺度空间设计中存在的诸多弊端和居民对水景的需求之间存在矛盾，营造赏心悦目的绿色水景，创建一个安全、优美、舒适的人居环境是小尺度空间中水景应用急需探讨和解决的问题，也是设计工作者面临的重大课题[16].

3.2 公式可靠性分析

国内外对管节点热点应力分布的研究较少，目前仅伦敦大学学院（UCL）的Hellier 等［9］和Chang等［10］分别建立了两套热点应力分布计算公式，计算公式及其适用范围如表4所示.

表4 现有SCF分布计算公式Tab.4 Existing SCF distribution curve formulae

Hellier 公式和Chang 公式均建立于有限元参数分析结果的基础上，有限元模型采用壳单元.Hellier公式和Chang 公式仅以一个T 形相贯节点试验［19］进行了验证，节点参数如表2 中节点T3所示，其可靠性和适用性有待更多试验验证.因此，本文在此基础上引入了南洋理工大学（NTU）试验［3，18］，如表2 中节点T1、T2所示.

根据表2 中试件的几何参数分别计算了Hellier公式计算值SCFhellier（δ）及Chang 公式计算值SCFchang（δ），然后根据标准化原则将SCFhellier（δ）、SCFchang（δ）及试验测量值SCFE（δ）标准化为DIShellier、DISchang、DISE，并用本文拟合公式（6）计算了表2 中试件的应力分布系数值DIS本文公式，最后将DIShellier、DISchang、DIS本文公式（统称为DISF）与DISE进行比较，以验证本文公式的可靠性.

根据公式计算结果绘制了本文公式DIS 曲线、Hellier公式DIS曲线及Chang公式DIS曲线并对试验数据描点，如图14所示.需要说明的是，对于T3节点，Hellier公式和Chang 公式的DIS曲线完全重合.通过对比各公式曲线与试验数据点可看出：本文公式曲线与Hellier公式曲线在所有情况下均基本反映了试验点的变化趋势，而Chang 公式曲线则存在以下主要问题：1）节点T1、T2的Chang 公式曲线在冠点不连续且有明显突变，即冠点位置的计算结果不等于0，某些情况下（如表2中的γ较小的节点T2），冠点附近的DIS达到0.8，与实际严重不符；2）分布曲线关于π/2 呈现轻微不对称，这与实际不符；3）Chang 公式中参数C0、C1、C2的表达式过于复杂，不便于实际工程应用.

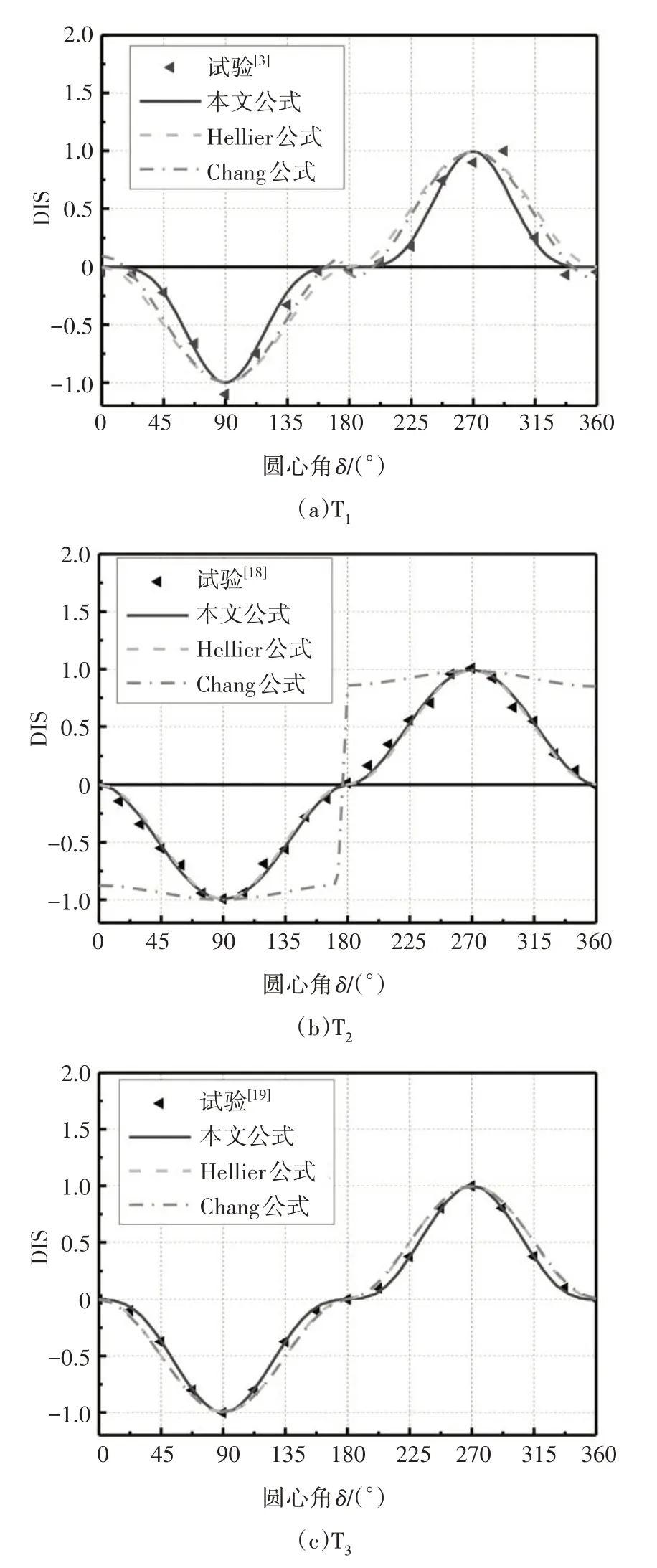
图14 DIS曲线对比Fig.14 Comparison between DIS curves

为了进一步比较DISF与DISE的吻合程度，对其比值R=DISE/DISF进行了量化统计分析，对比了三个公式的R分布，由于Mopb作用时冠点的理论应力值为0，Mopb作用时冠点相邻点的试验应力值较小，这些位置的R值没有意义，对比时剔除了这些数据点.表5给出了Mopb作用时节点鞍点及冠点的R值主要统计参数（最大值Rmax、最小值Rmin、均值μR、标准差σR以及变异系数VR）.

表5 R样本分析的主要统计参数Tab.5 Main statistical parameters of R sample analysis

可以看出：Mopb作用时，Hellier 公式和Chang 公式相应的μR均大于1.0，其中Chang 公式计算值明显大于试验值，本文公式对应的μR基本等于1.0；同时Hellier公式和Chang公式对应的σR均超过0.40，其中Chang公式对应的σR甚至超过了0.60，本文公式的离散性明显好于其他两个公式，表明Mopb作用时本文公式较Hellier 公式和Chang 公式更好地反映了试验情况.

总体而言，本文公式在均值和离散性两个方面均与试验结果吻合良好.

4 结论

本文在径向拉伸模型的基础上对T 形圆管相贯节点在平面外弯矩作用下的热点应力分布进行了有限元参数分析，根据有限元参数分析结果拟合了热点应力分布系数DIS 计算公式，将本文计算公式、Hellier 公式、Chang 公式与试验数据分别进行了对比，得到以下结论：

1）不同密度网格有限元模型对比显示，热点应力的计算结果均具有很好的收敛性，基本网格满足计算精度的要求.

2）有限元计算结果显示，Mopb作用下的DIS 曲线形状满足正弦三角函数形式，波幅为2，函数周期为2π；几何参数分析结果表明，不同几何参数对DIS 曲线形状影响不同，其中受α、τ影响较小，而随着β、γ的增大，DISopb曲线冠点位置逐渐出现反弯点，并呈现反弯平台段，平台段宽度逐渐扩展至冠点±30°，鞍点附近的曲线斜率相应变大.

3）将公式与试验对比结果分别进行了样本的统计分析，结果显示本文公式在Mopb作用下均表现出较好的均值和较低的离散性，较Hellier公式和Chang公式可靠性更高，也与试验结果更为接近.

4）本文建立的T 形圆钢管相贯节点在平面外弯矩作用下的DIS 计算公式具有较高的可靠性，为实际工程提供了设计依据，也为后续研究组合荷载下热点应力极值奠定了基础.