适用于随机车流的二维桥梁动态称重应用

谭承君，赵华†，张斌，郭泓捷

（1.湖南大学土木工程学院，湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082）

超载车辆严重威胁公路桥梁的安全运营.针对超载现象，世界各国推出了一系列惩罚措施进行控制，但如何高效识别超载车辆是各国交通部门面临的挑战.传统的静态称重是最直接、最准确的检测方法，但该方法效率低，且在一定程度上阻碍交通.为解决此问题，20世纪中期，欧洲率先提出了车辆动态称重（Weigh-in-motion，WIM）技术，即车辆在行驶过程中被称重［1］.早期的WIM 系统通过埋置在路面的传感器识别车辆轴重信息，因此也被称为路面称重系统.该类方法因传感器截面尺寸小，车辆-传感器相互作用时间短等，导致车辆轴重识别精度不高［2］.此外，在安装、更换传感器时，WIM 系统需在路面开挖基坑，中断交通，且传感器也存在耐久性问题［3］.

针对WIM 技术的不足，桥梁动态称重（Bridge weigh-in-motion，BWIM）技术被提出.该方法通过测量移动车辆荷载作用下的桥梁响应信号，利用反问题求解方法反算出车辆轴重等信息.BWIM 系统中的称重传感器安装于桥梁下方.与WIM 系统相比，BWIM 系统具有以下优点：1）质量轻，体积小，方便运输和转移；2）安装及测试隐蔽，能够检测真实交通状况；3）桥梁长度比路面称重系统中的秤台长，车桥相互作用时间长，因此称重精度受车辆动态载荷的影响小；4）安装、测试、更换时不需中断交通［4-5］.

全球多个地区已开展了BWIM 技术现场应用研究，试验桥梁也包含有混凝土简支T 梁、正交异性钢桥面、斜拉桥、混凝土连续箱梁等［6-9］.经过40年的发展，目前BWIM 技术不仅发展成为车辆静态称重的有效补充手段，同时也能为交通监控、交通运输管理等方面提供有力数据基础［10］.近来，Gonzalez 等［11］和Obrien 等［12］基于机器学习或数理统计方法，利用BWIM 数据提出了有效的桥梁损伤检测方法，进一步提升了BWIM技术应用范围.

BWIM 技术一般基于Moses 算法［13］识别车轴重量.Moses 算法是根据桥梁结构影响线，利用桥梁响应信号来计算车轴轴重.传统Moses 算法通常将桥梁视为一维结构，与实际桥梁的二维结构受力特性不符.为此，Quilligan等［14］和Yu等［15］将一维Moses算法扩展到二维空间，提出了利用结构影响面来考虑桥梁的二维特性，但获取结构影响面十分困难，现实中难以实现.此外，龙波［16］提出了利用车道影响线来提高宽桥中Moses算法识别精度，即不同车道拥有不同的影响线.Zhao 等［17］考虑了桥梁的横向分布效应，提出了基于多条结构影响线的二维BWIM 算法.虽然这些方法考虑了桥梁结构的二维特性，但仍然无法解决BWIM 技术实际应用中最大的挑战——多辆车同时经过桥梁时的轴重识别难题.

宫亚峰等［18］基于桥梁弯矩影响面来处理多车并存时每个车轴识别问题.但如上所述，结构影响面在实际应用中难以准确获得，极大地限制了该方法的工程实际应用.Chen 等［19］提出了一种基于长距离光纤布拉格光栅传感器的BWIM 系统，该系统利用传感器信号所形成的面积来计算车轴轴重.目前该方法仅仅通过室内简化模型进行了验证，其实际应用可行性还有待进一步验证.

本文提出了一种不考虑影响面的2D-BWIM 算法.该方法通过获取桥梁每片梁的影响线以及实时的横向分布系数来提高随机车流中车轴识别精度.同时针对多车并存，该算法提出了基于横向分布系数的迭代方法.本文首先基于理论分析，推导了2DBWIM 算法的计算公式，然后通过基于实际桥梁的标定试验以及三次随机车流试验验证该算法的准确性和可行性.

1 BWIM现场试验

现场试验桥梁为3×12.8 m 的三跨全预应力混凝土简支T 梁结构，位于美国亚拉巴马州78 号高速公路.该试验由本文作者参加完成，详见文献［20］.试验桥梁立面图如图1所示.桥梁上部结构由4片T梁构成（见图2），且每片T梁跨中梁底安装一个应变传感器，称之为称重传感器.此外，为了获得行驶过桥的车辆有效信息，每个车道布置有一对FAD（Free of Axle Detector）传感器.

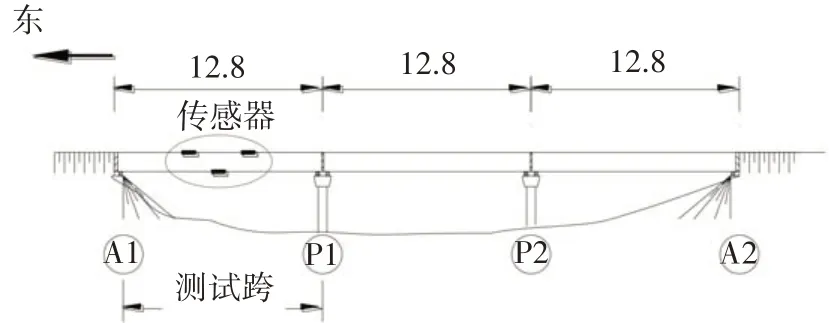
图1 试验桥梁立面图（单位：m）Fig.1 Elevation of the test bridge（unit：m）

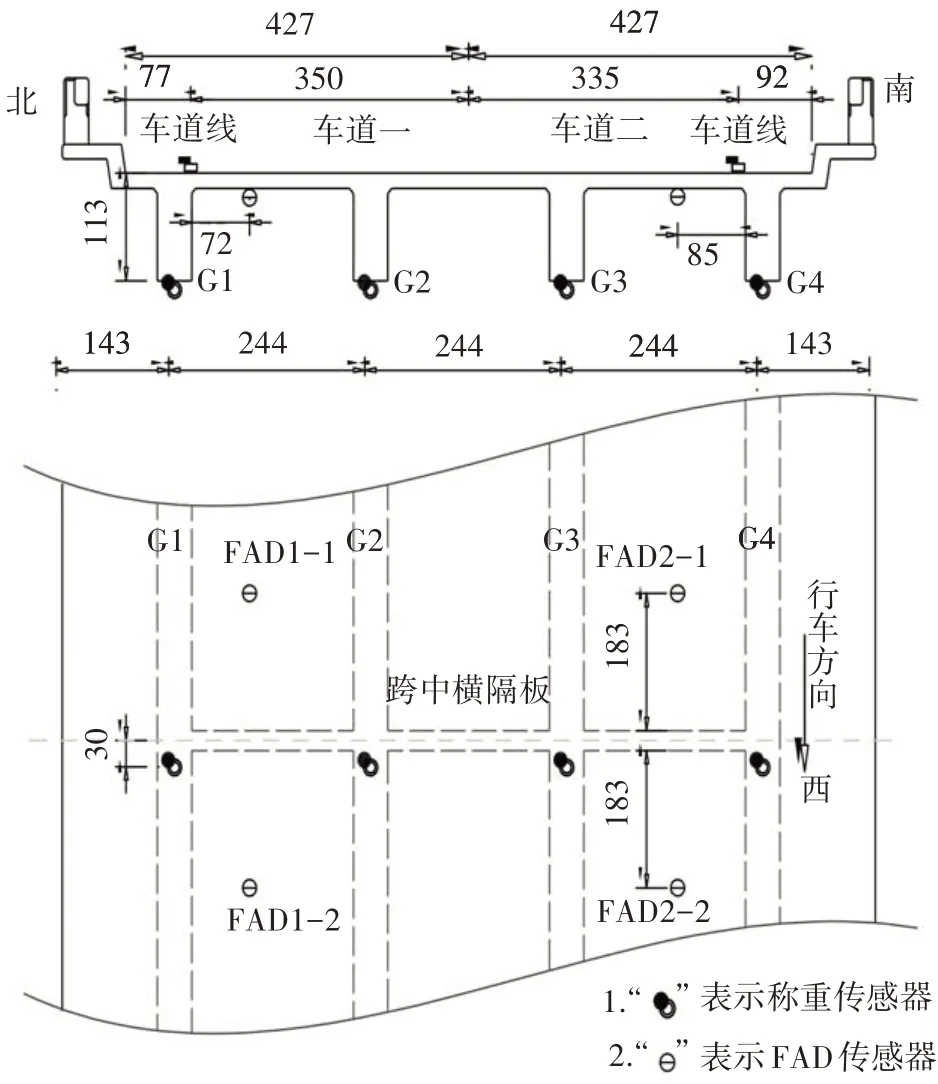
图2 传感器布置示意图（单位：cm）Fig.2 Schematic diagram of sensor layout（unit：cm）

1.1 标定试验

标定试验车辆为两辆5轴车，具体参数如表1所示（标记为车辆A 和B）.标定试验过程可详见文献［17］.车辆A 和B 分别沿车道一、二重复5 次跑车试验（共计20趟）.此外，试验中车辆A 和B同时经过试验跨一次.试验采样频率为500 Hz.

1.2 随机车流试验

随后，课题组开展了该桥在实际车流下的BWIM 系统测试研究.如图3 所示，为了检测BWIM系统识别精度，在测试期间，经过测试桥梁的所有卡车（忽略小车）均会在距离试验跨不远处被当地交警拦下，利用可携带地磅进行静态称重.因此，该随机车流试验仅仅关注卡车，相互影响车道数为两个车道，且车辆沿同一方向行驶，试验过程中均为正常交通状况.随机车流试验共进行3 次，每次持续几小时，表2 记录了试验所有卡车分布情况，其中，共记录了8次多车过桥事件.

表2 随机车流测试中卡车分布情况Tab.2 Distribution of trucks in random traffic

图3 随机车流BWIM系统测试Fig.3 BWIM test under random traffic

2 2D-BWIM 算法理论

2.1 桥梁结构影响线

Obrien 等［21］提出了利用最小二乘法来获得目标桥梁实际影响线，计算公式见式（1）.

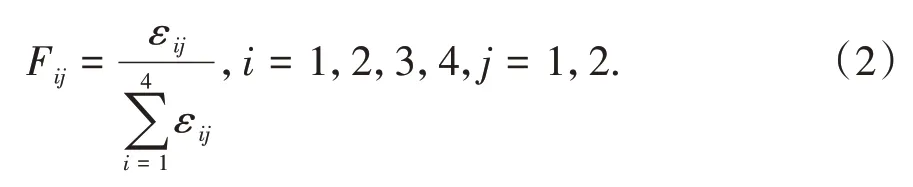
式中：εij为车辆沿车道j经过桥梁时，桥梁最大响应时刻梁i#的响应值（因为响应幅值大时受噪声信号和桥梁振动的影响相对更小）.显然，Fij为车道荷载下横向分布因子，车辆在不同车道时，其分布因子是不同的.根据上述标定试验跑车20 趟（每个车道10趟），车道一的梁1#～4#的横向分布系数（平均值）分别为0.36、0.40、0.21、0.03；车道二的梁1#～4#的横向分布系数（平均值）分别为0.08、0.22、0.43、0.27.

当车辆沿车道j经过桥梁时，对于每一片梁，根据公式（1）可以得到：

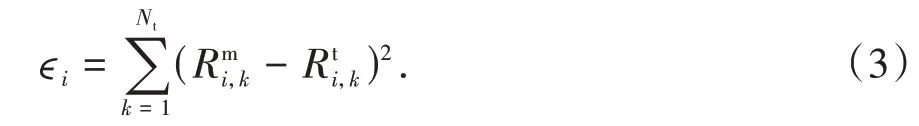
式中：Na为车轴数目；As为车轴重量；Ik-Ps为k时刻下第s车轴对应结构影响线的坐标值；Ps为第s车轴与第1 个车轴之间的采样滞后点，可以通过Ps=Ds f/v计算得到，其中Ds为第s车轴与第1 个车轴之间间距，f为采样频率，v为车速.因此，上述公式（3）可以另表述为：

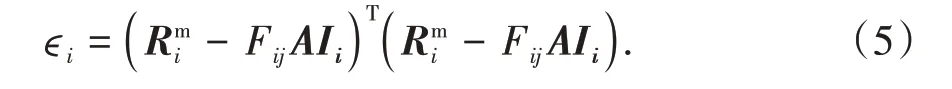
由此，通过标定试验可获得每片梁的实际影响线：

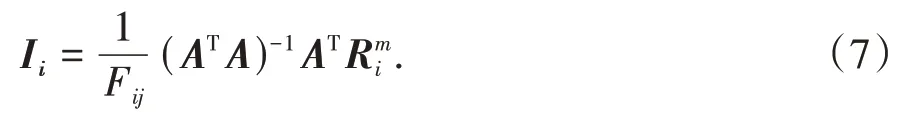
如式（7），由于不同车道荷载下Fij有所不同，因此，不同车道荷载下计算的Ii也不相同.理论上，在标定试验中，无论是车道一或车道二，根据公式（7），都能获得梁1#～4#对应的结构影响线，但一般来说，响应幅值越大，其抗信号干扰能力越强，保真度越高，因此，梁1#、2#的影响线通过标定车辆沿车道一的跑车来获得，而梁3#、4#的影响线通过标定车辆沿车道二的跑车来获得.相对应地，梁1#、2#的影响线仅用于车道一的移动荷载识别，而梁3#、4#的影响线仅用于车道二的移动荷载识别.图4 为标定试验中所得到的梁1#～4#的平均影响线.

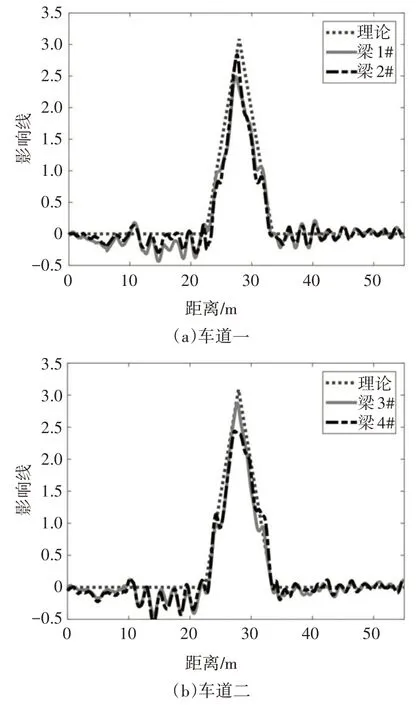
图4 桥梁结构影响线Fig.4 Bridge structural influence lines

2.2 移动荷载识别

已知桥梁影响线求轴重时，上述公式（5）中和Ii是已知的，A未知.同理，为了获得最小ϵi，可对A求导，并令其为0，从而得到轴重计算公式：

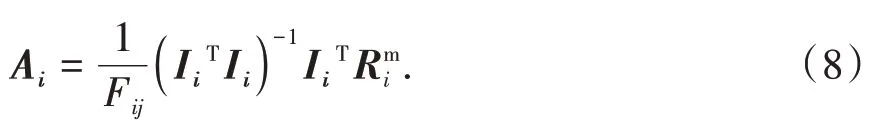
由公式（8）可知，理论上可以通过一片梁的影响线来计算轴重.为了降低偶然误差，可以利用梁1#、2#的影响线来共同计算车道一车辆荷载.一般情况下可以通过平均梁1#、2#的计算荷载作为车道一的最终车辆轴重.但是考虑到响应幅值越大其受噪声信号和桥梁振动的影响相对越小，保真度越高，因此本文对更大的幅值响应信号分配更高的权重，即按横向分布系数进行权重分配，计算公式见式（9）.

在随机车流中，根据公式（9）可以直接计算出单辆车经过桥梁时的轴重信息.为解决多车同时过桥的轴重识别难题，在2D-BWIM 算法基础上，本文提出了一种迭代方法，具体如图5所示.

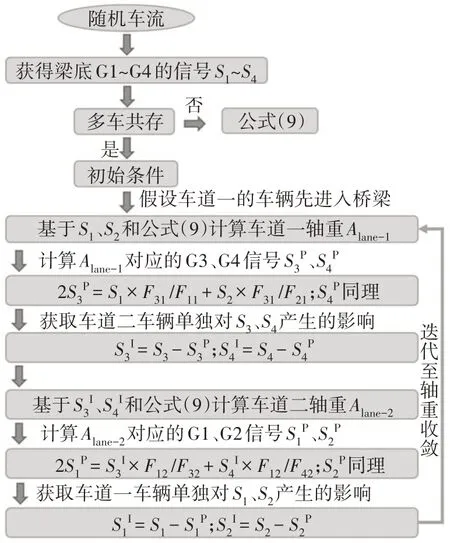
图5 多车事件中2D-BWIM算法（G1～G4为图2中梁）Fig.5 2D-BWIM algorithm in multi-vehicle presents（G1～G4 represents the girder as shown in Fig.2）

当多车事件发生时，BWIM 系统首先认为梁底响应信号仅为率先进入桥梁的那一辆车所产生.为了阐述方便，假设车道一的车辆先进入桥梁.根据公式（9），利用梁1#、2#响应信号S1、S2来计算车道一的初始轴重Alane-1，显然该计算结果将大于真实值，因为梁1#、2#部分响应信号由车道二的车辆所造成.同时，该算法提出一个假设，即梁底响应按照横向分布系数成比例缩放，因此，可以计算得到初始轴重Alane-1对梁3#、4#造成的响应信号同时，为了获得车道二车辆单独作用下对梁3#、4#造成的响应信号，将桥梁简单视为线弹性结构，可以利用梁3#、4#实测响应信号S3、S4分别减去计算生成信号得到车道二计算轴重的输入信号信号被放大（初始Alane-1被放大），输入信号与真实值相比降低了.因此，车道二初始轴重将明显小于其真实值，但经过迭代算法，Alane-1将逐渐减小而Alane-2将逐渐增加，直至轴重识别结果稳定，迭代结束.

如上所述，本文提出的迭代方法基于一个假设（即单辆车过桥事件中，梁底响应按照横向分布系数成比例缩放），下面将对该假设的准确性、有效性进行验证.图6 记录了标定试验中标定车辆A 沿车道一经过桥梁时所采集的信号.FAD1-1 和FAD1-2 信号均显示了5 个明显的峰值信号，对应于车辆A 的5个车轴经过对应传感器的时刻，根据FAD1-1 与FAD1-2中对应峰值信号时间间隔及其实际距离，则可以获得该车辆的实际速度，然后根据FAD1-1 或FAD1-2 信号中峰值信号时间间隔和车速便可以计算出车辆的轴距参数［8］.

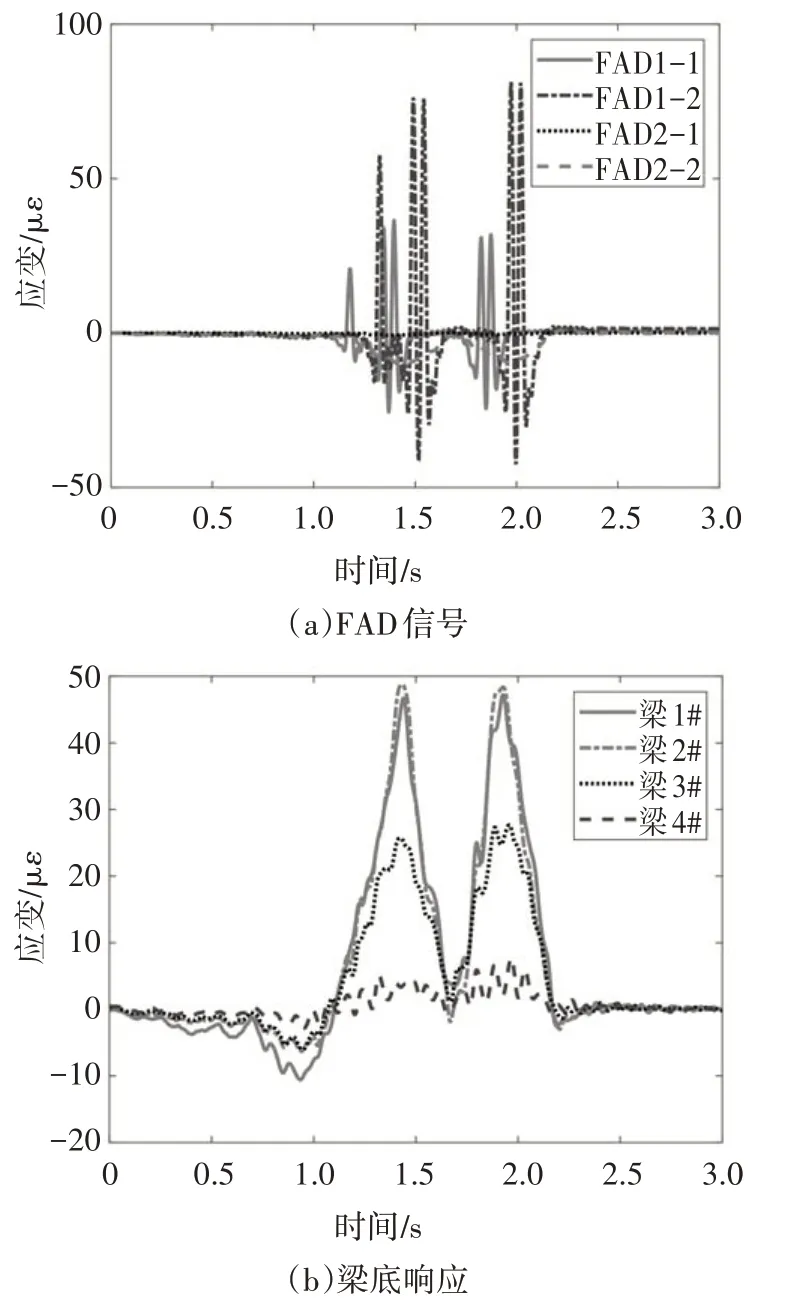
图6 标定试验车道一跑车信号Fig.6 Calibration test on lane 1

图7 显示了该趟跑车下基于假设计算出的生成信号与实测信号之间的差异，即利用梁1#、2#响应信号以及横向分布系数计算梁3#、4#的生成响应信号.其中“计算1”结果根据该趟的横向分布系数获得，“计算2”结果根据车道一的10 趟标定试验平均横向分布系数获得.由图7 可见，梁3#、4#中“计算1”与“计算2”之间的差别甚小，而且它们与实测结果也都非常接近，其绝对误差值很小.本文利用平均误差值来量化基于此假设下的计算误差：

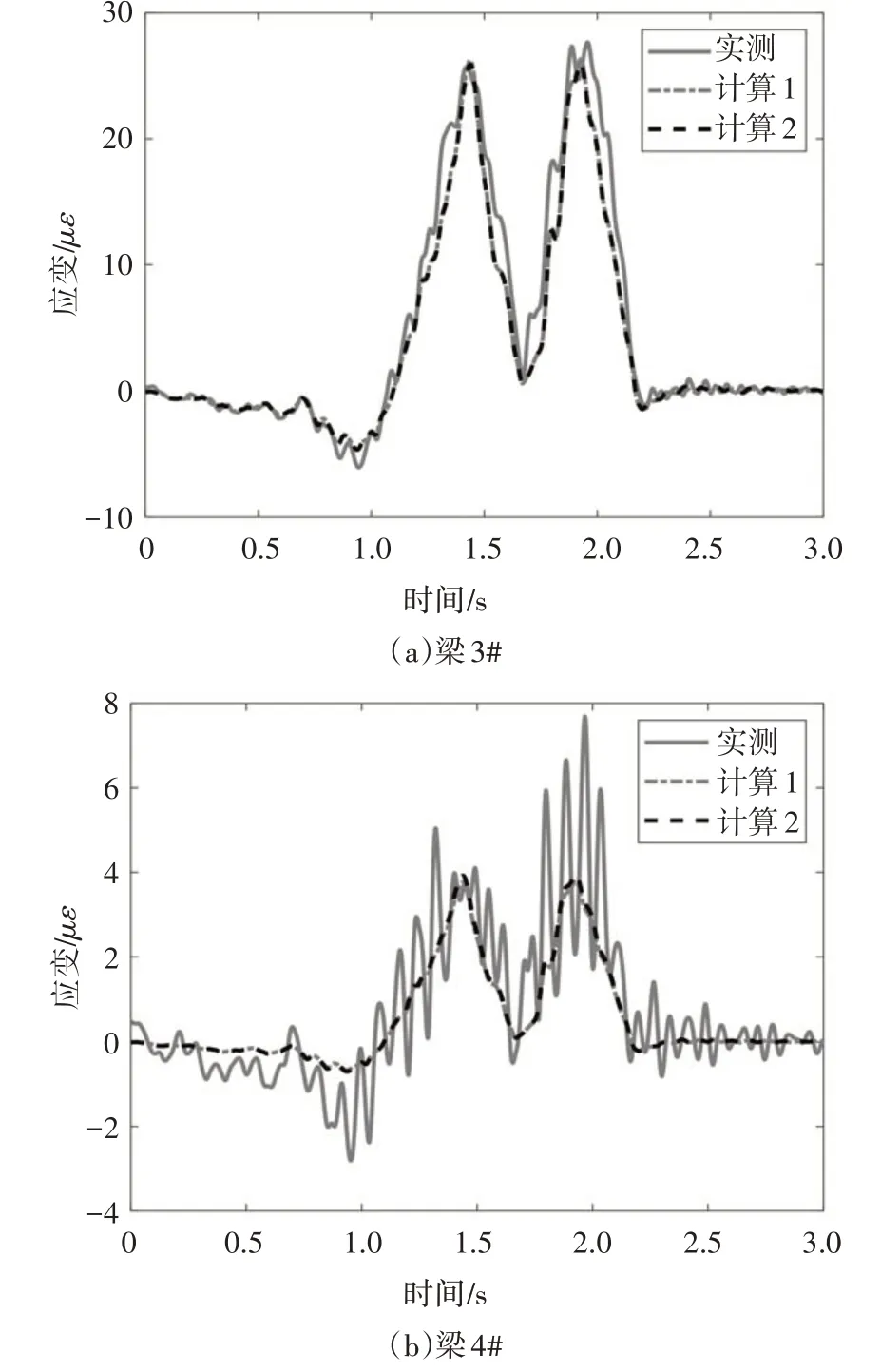
图7 理论与生成信号之间的差异Fig.7 The difference between the theoretical signal and the generated signal

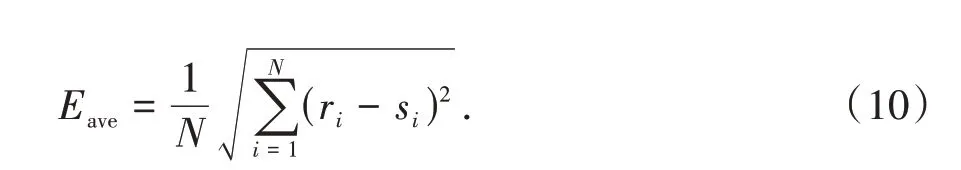
式中：ri为计算生成信号；si为实测信号；i为时间步长；N为信号采集长度.值得一提的是，多车并存事件中，每一辆车的实时横向分布系数无法通过公式（2）获得.考虑到多车并存时，各个车道的车辆均不会明显偏离其车道中心线，车辆行驶轨迹与标定试验相差不大（标定试验中车辆大致沿车道中心线行驶）.因此，针对多车并存事件，各车道的横向分布系数可以采用标定试验中平均横向分布系数计算，即采用“计算2”结果.根据公式（10），该趟跑车平均误差如图8第1趟所示.

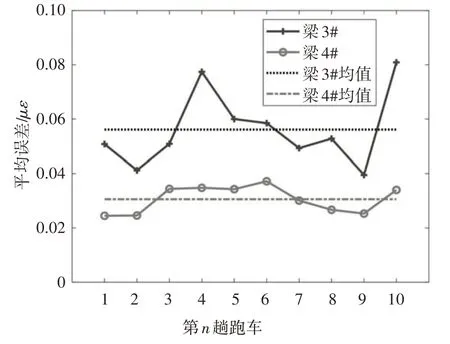
图8 车道一预测信号误差分布Fig.8 Generated signal error distribution on lane 1

此外，图8绘出了标定试验中车道一其余9趟计算生成信号的误差结果.对于这10 趟标定试验，梁3#、4#平均误差值分别为0.056 13με、0.030 59με，其标准差分别为0.013 74με、0.049 18με，可见，基于该假设计算生成的响应信号的绝对误差值均非常小，结果离散度也很小.这些结果亦表明，基于横向分布系数，利用主响应信号预测非主响应信号的准确性很高，其绝对应变误差值非常小，而BWIM 系统计算轴重算法与梁底信号应变绝对值相关.因此，可初步得到以下结论，迭代方法提出的假设对后续BWIM系统中移动车辆轴重及总重的识别精度影响较小.

2.3 多车并存时2D-BWIM算法的验证

为了进一步验证多车共存时2D-BWIM 算法中迭代方法的准确性，以标定试验中两辆标定车同时经过桥梁（标定车A 沿车道二行驶，标定车B 沿车道一行驶）的工况为例，利用2D-BWIM 算法识别移动车辆A 和B 的轴重及总重.图9 记录了该工况下FAD 传感器信号和梁底响应信号.如图9 所示，车道一、二的FAD 信号均显示5 个明显峰值，且发现车道二的标定车A较先进入桥梁.

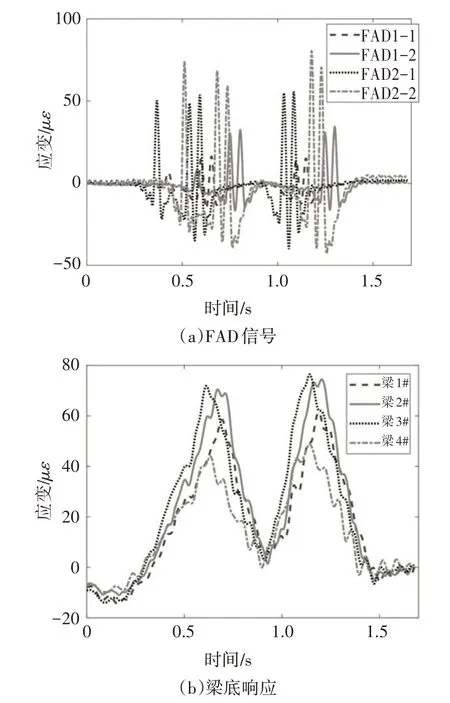
图9 标定车A和B同时过桥信号Fig.9 Signals of two calibration trucks cross the bridge

利用图5 算法对该多车并行工况进行轴重识别，其结果如图10所示.与上述分析一致，车道二的车辆率先驶入桥梁，因此车道二初始轴重识别结果明显大于其理论值，反之，车道一初始轴重小于理论值，经历7 次迭代，最终车道一和车道二总重识别误差分别为-3.26%和2.68%，其单个轴重识别误差分别不超过-5.89%和-6.11%，进一步验证了图5 算法的可行性与准确性.

图10 迭代中轴重识别结果Fig.10 Axle weight recognition results in iteration

3 随机车流试验结果分析

随机车流试验中传感器布置与标定试验一致，可以通过FAD 传感器来识别行驶车辆的车道分布、速度、车轴数量和车轴间距.三次随机车流测试中，绝大部分车辆车速位于55～105 km/h，组轴（轴距非常近，约1.4 m）轴距识别最大误差为16.0%，其误差平均值和方差分别为7.1%和3.9%；非组轴轴距识别最大误差为8.4%，其误差平均值和方差分别为0.7%和1.7%.车轴轴距识别精度较高，在可接受范围内.

3.1 随机车流中单辆车过桥事件测试结果

针对上述三次随机车流测试中每一趟单辆车过桥事件，分别利用传统Moses 算法以及本文提出的2D-BWIM 算法对其进行轴重识别，车辆总重识别结果如图11所示.结果表明，随机车流测试中Moses算法存在较大的识别误差，且结果离散度较大.其原因主要有以下两点：1）当仅有一辆车经过目标桥梁时，车辆可能严重偏离行驶，即车辆行驶中心线与对应车道中心线偏离较远；2）一些卡车处于空载状态，车皮重较轻（比如2、3 轴车），因此，尽管识别绝对误差值可能不大，但其误差百分比可能较大.本文提出的2D-BWIM 算法考虑了车辆过桥时实时的横向位置，因此，该2D 算法能够大幅提高车辆总重识别精度.对三次随机车流测试中所有单辆车过桥事件进行统计分析，Moses 最大识别误差为47.3%，而2D-BWIM算法总重识别误差在13.7% 以内，Moses 与2DBWIM 算法对车辆总重识别误差平均值分别为7.9%、3.1%，识别误差方差分别为13.5%、4.8%.

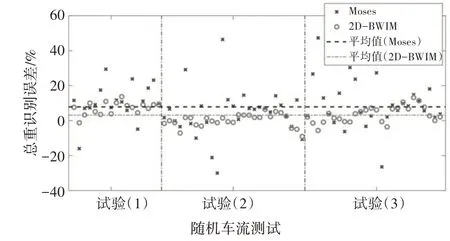
图11 随机车流中车辆总重识别误差Fig.11 The result of total weight identification errors under random traffic

图12 通过箱形图绘出了随机车流测试中单个车轴轴重识别误差分布图.箱形图是一种常见的统计图，能够表现出一组离散数据的上边缘、下边缘、中位数和两个四分位数，以及数据异常点.由图12可见，相较于Moses算法，2D-BWIM 算法的轴重识别精度更高，且具有明显的较小离散型.（2D-BWIM 算法，Moses算法）在试验（1）（2）（3）中的轴重识别误差中位数分别为（7.8%，13.1%），（1.0%，3.9%）和（3.6%，7.2%）.综合三次随机车流试验，2D-BWIM 算法和Moses算法识别误差箱形图中的上边缘、上四分位数、中位数、下四分位数和下边缘分别为（25.6%、8.3%、3.6%、-1.1%、-17.6%）和（53.6%、16.9%、6.9%、-1.8%、-35.7%）.由此可见，尽管剔除了一些奇异值，Moses算法针对随机车流中的轴重识别精度离散程度依然很大，本文提出的2D-BWIM 算法考虑了车辆实时的横向位置，其轴重识别精度明显高于传统Moses 算法，且算法保真度较高，轴重识别误差离散程度非常小.

图12 随机车流中车辆轴重识别误差箱形图Fig.12 Box plot of recognition errors under random traffic

3.2 随机车流中多车并存事件测试结果

多车事件是指某一辆车未完全驶出桥梁时，有另外一辆车已驶入桥梁.由于试验桥梁跨径小，多车事件均为一、二车道上同时各出现一辆车.图13 显示了试验中两次多车事件的现场照片.3 次试验中多车事件的轴重及总重识别结果如表3所示.8次多车事件均为一辆卡车与另外一辆小（货）车同时经过桥梁的情形，其中1、2、8 工况的卡车沿车道一（快车道）行驶，小车沿车道二行驶，其余工况的车道分布与之相反.事实上Moses 算法没有处理多车并存时的特定办法，仅仅是认为该卡车单独经过桥梁（认为另一车道上无车辆经过）.由于小车本身重量较轻，Moses算法对其总重识别结果可能影响不大，而对车辆轴重识别结果影响可能更为突出.如表3所示，本文提出的2D-BWIM 算法能够显著提高其中卡车的轴重识别精度.针对表3中8趟多车并存工况，Moses算法轴重的识别误差平均值和方差分别为3.12%和26.33%，2D-BWIM 算法轴重的识别误差平均值和方差分别为1.53%和7.34%.其中，Moses算法最大轴重识别误差高达58.3%，而2D-BWIM 算法的轴重最大识别误差仅为-13.5%.多车事件中，由于多辆车同时作用，因此无法根据文中公式（2）来计算每一辆车的实时横向分布系数，本文利用了标定试验值进行计算.不可否认，多车事件中实际横向分布系数与标定试验存在一定的差异，但由于多辆车并存时，车辆的偏离程度很小，因此这种差异不大，结果也表明，该方法识别的轴重精度在可接受范围内.

图13 随机车流中多辆车同时过桥照片Fig.13 Multi-presents photo under random traffic

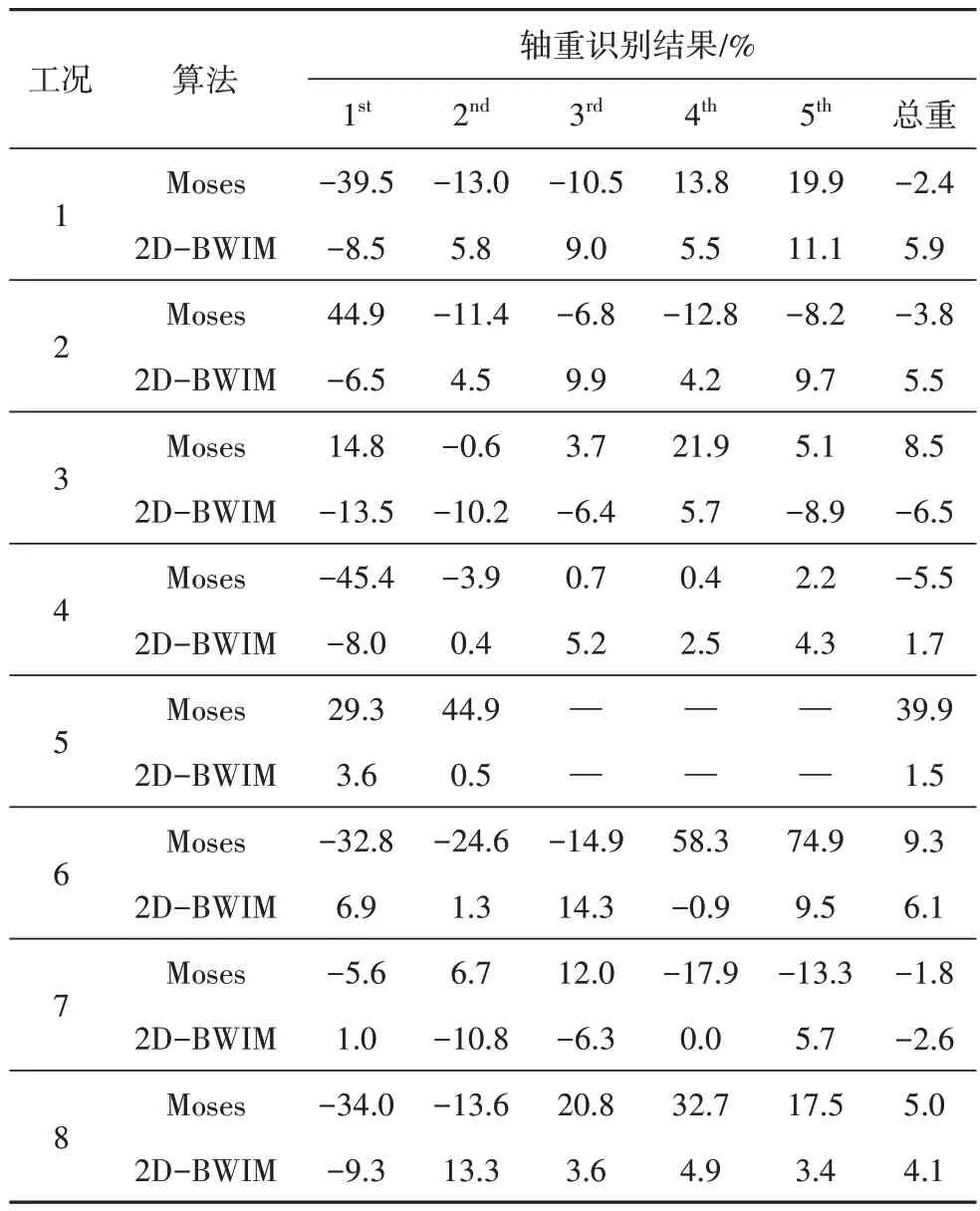
表3 随机车流中多辆车同时过桥时轴重识别结果Tab.3 Axle weight recognition result in multi-presents

4 结论

1）基于桥梁的二维结构特性，本文提出了一种适用于随机车流的2D-BWIM 算法，并通过理论推导、标定试验以及随机车流试验综合验证了该算法的可行性及准确性.

2）针对单辆车经过目标桥梁的情况，相较于传统Moses 算法，2D-BWIM 算法考虑了车辆的实时横向位置，因而能够显著提高车辆轴重及总重识别精度.根据3次随机车流测试结果，（Moses、2D-BWIM）算法的总重识别误差平均值及方差分别为（7.9%、3.1%）和（13.5%、4.8%）.

3）基于一种假设，2D-BWIM 算法提出了多辆车同时经过桥梁的轴重识别算法，在随机车流试验中显现出了良好的识别精度.由3 次随机车流试验的多车过桥事件结果可知，（Moses、2D-BWIM）算法的轴重识别误差平均值及方差分别为（7.34%，1.53%）和（26.33%，3.12%）.

4）分析结果表明，相较于传统Moses 算法，2DBWIM 算法能够有效提高过桥车辆轴重及总重的识别精度.该算法不受桥梁跨径限制，但是，目前2DBWIM 算法仅在拥有两个车道（车辆沿同一方向行驶）且车辆均正常行驶情况下进行了验证，该方法针对其他复杂交通状况以及更多车道的桥梁的有效性还有待进一步研究.