基于点云数据与工程知识的桥梁形态变化识别方法

熊文，李刚，张宏伟，张立奎，操川

（1.东南大学交通学院，江苏南京 211189；2.安徽省交通控股集团有限公司，安徽合肥 230088）

将三维激光扫描技术运用于桥梁空间变形识别时，一般需在不同时间点对桥梁结构进行数字化扫描并得到其形态点云模型，通过不同时期点云配准［1］，得到对应点间距离差值即为该时间段内桥梁空间形态变化.因此，点云配准算法的可靠性决定了桥梁形态变化识别结果的准确性.尤其对于百万数量级点云模型的大跨度桥梁形态分析，其精度与效率间的平衡控制面临着巨大挑战［2］，配准方法的科学性直接影响桥梁状态评估的准确性［3］.

点云配准的本质是将待配准点云Q根据某一空间转换矩阵进行变换，变换后与参考点云P处于同一坐标系［4］；该空间转换矩阵包含旋转矩阵R和平移矩阵T.目前点云配准常用“迭代最近点法”，即ICP（Iterative Closest Point）算法［4］.该算法基于最小二乘的最优匹配，其不断重复“确定对应关系的点集—计算最优刚体变换”的过程，直至达到某一匹配收敛准则.具体来说，针对待配准点云Q与参考点云P中的所有邻近点对（pi，qi），求解出使某一误差函数最小的旋转矩阵R与平移矩阵T，该误差函数为邻近点对中对应点的距离方差之和；理论上矩阵求解时点对越多，则配准精度越高［5-7］.

为不断提升ICP 算法的精准性与适用性，许多学者从算法本身展开研究.Besl和Mckay［8］基于欧式距离最近点对应原则，以对应点间距作为误差指数，利用四元数法求解转换矩阵.Chen 和Medioni［9］以点面距离作为误差指数，同样通过迭代得到转换矩阵.在提高算法效率上，部分学者基于特征度量对算法进行改进.Sharp等［10］提出基于欧几里得不变特征的算法；邹际祥［11］利用KD-tree 进行最近邻搜索.在提高算法精度上，Jost 和Hugli［12］提出迭代中逐步增加点的多层次ICP 配准方法；Zhang［13］通过施加距离与夹角约束，排除不适合参与配准的点对；Dorai 等［14］则利用可信程度约束排除错误点；Simon等［15］提出旋转矩阵与平移矩阵相互独立的计算方法.

ICP 算法在点云初始对齐形态较好且数据复杂性较低时能够得到较好的配准结果［4］.但是，该算法用于桥梁形态点云配准时，其“针对点云中所有对应点对进行配准”的特性可能会造成结果的不可靠性，其原因在于：桥梁点云中总有一些点发生绝对位置变化（刚体位移），若这些点也参与配准，则配准后点云间的配准残差不仅包括各点真实变形值（弹性连续位移），也包括发生位置变化（刚体位移）的点在配准时所引起的变化误差.若将存在配准误差的残差值作为各点变化量，则桥梁形态变化识别结果与真实情况不符，甚至不遵循常规的结构力学原理，最终导致桥梁状态的错误评估.

针对上述技术难题，提出一种基于点云模型与工程知识的桥梁形态变化识别方法.该方法首先获取不同时间点的桥梁三维点云模型，根据桥梁运营空间形态变化特征，将桥梁结构中位置/坐标稳定点视为相对不动点，仅使这些不动点参与配准迭代过程.进而以上述优化后的点云模型为分割与配准主体，完成桥梁形态变化的精准识别，并基于结构力学基本规则对结果进行验证.最后，以一座大跨连续刚构桥的实际工程应用为例，证明了该方法用于桥梁服役状态评估时的合理性与适用性.

1 基于工程知识的点云配准算法

1.1 配准原理

传统ICP 配准算法使用点云中所有点对参与配准，未考虑已发生位置变化的点对配准过程的影响，可能会造成变形识别的不准确［16］.本文提出一种基于工程知识的点云配准算法，即根据既有工程知识，指定桥梁特定位置点为相对不动点来参与配准的三维点云配准算法.

由于荷载传递与分配以及桥梁结构体系特征，桥梁不同位置所发生变形的程度可能具有显著的差异性.根据实际工程知识与结构变形规律，可预断某些特定位置点云变形相对其他位置明显较小，将此处点云视为相对不动点并参与配准，能够大幅度降低干扰点对配准过程的影响，从而显著提高配准精度.

由于单体构件不同位置处变形差异更具规律性，更易选择相对不动点，因此，该算法用于桥墩、主梁等单体构件配准时，预期效果更佳.例如，梁桥长期运营后，其变形规律一般表现为墩顶水平位移大于墩底水平位移，同时主梁跨中竖向挠度大于支座处竖向挠度.显然依据上述工程知识，仅需选择墩底与梁端点云为相对不动点参与整体桥梁结构的配准过程.

1.2 配准算法

图1 给出了所提出配准算法的基本流程.该算法可视为不定迭代次数的循环过程.根据每次获取的构件空间变形，判断该次配准结果是否达到此配准算法下的最高准确度.图1 中旧构件点云与新构件点云分别为较早与较晚时间点采集得到.由于某时间段内新点云所发生变形建立于旧点云之上，故配准过程一般将旧点云作为参考点云，而将新点云作为待配准点云.

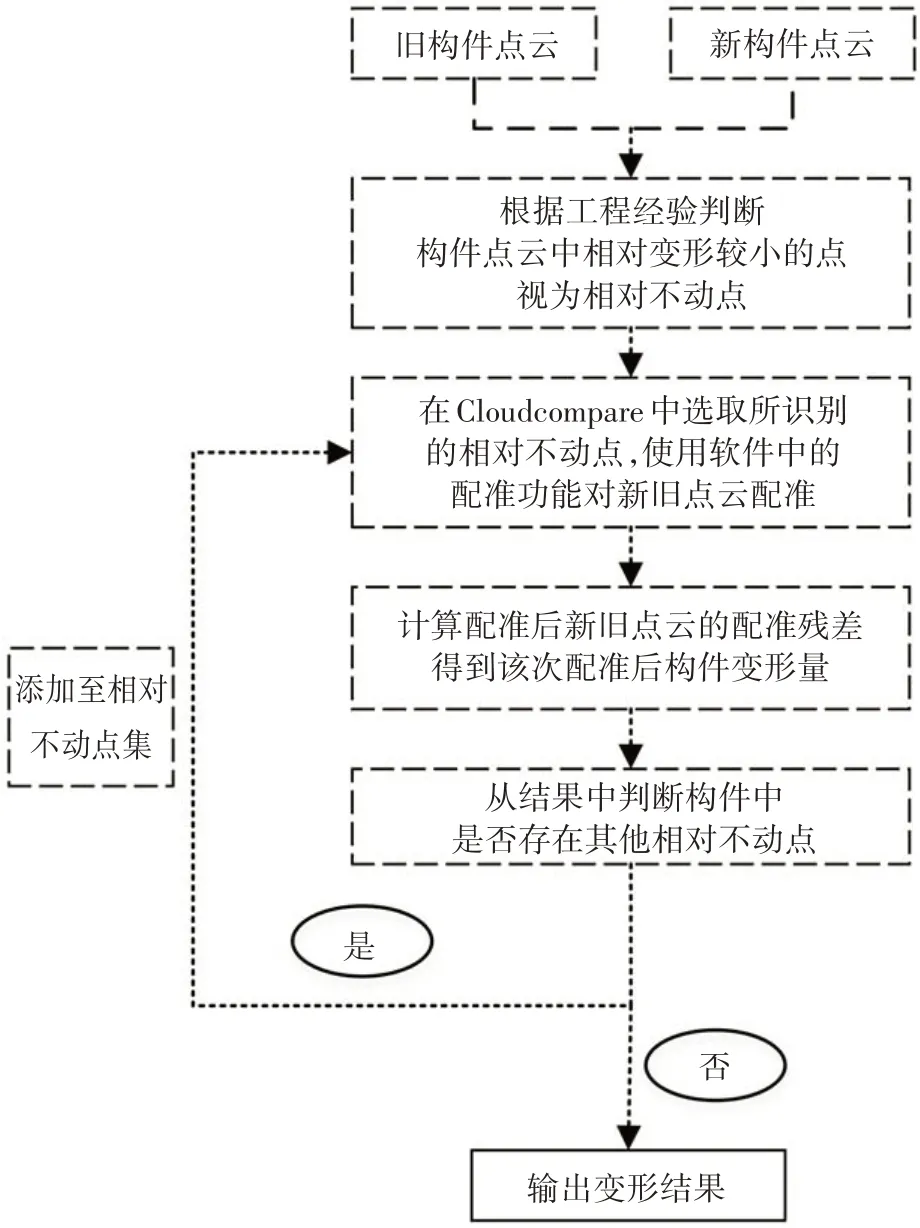
图1 配准算法流程Fig.1 Flowchart of registration algorithm

分割得到单体桥梁构件点云后，根据该构件结构特征以及工程知识，判断构件变形较小的点云区域，并将其视为相对不动点.以图2 为例，选择主梁两端处点云作为相对不动点，以此计算空间转换矩阵点对，得到相应空间转换矩阵.将该空间转换矩阵应用于新点云，完成其沿坐标系平动与绕坐标系转动的空间变换，即可实现该次配准下新旧点云坐标系的统一.

图2 基于工程知识的相对不动点选取Fig.2 Selection of fixed point cloud based on engineering knowledge

新旧点云坐标系统一后，仅需计算两点云对应点间距离，即配准残差，即可得到该时间段构件各处空间变形增量，点云中不同颜色代表其空间变形程度.

最后，判断变形结果中是否存在其他未发生变化或变形可忽略的点云区域.若存在，则在下次循环中将该点云补充并入相对不动点集，重复配准过程，得到新的变形结果；若不存在，则结束当前循环，输出该次变形结果.

2 基于工程知识的桥梁形态变化识别

2.1 形态变化识别流程

基于所提出的工程知识点云配准算法，图3 给出了桥梁形态变化识别的完整流程，包括配准前处理、配准算法运行、识别结果验证与导出三大模块.

图3 形态变化识别流程Fig.3 Flowchart of shape change identification

首先按一定规则将点云分割为独立构件单元.分割过程包括结构骨架化以及通过识别关键节点划分不同构件.然后使用所提出的基于工程知识的配准算法对新旧点云进行配准，得到桥梁各构件空间形态变化数值，同时利用形态变化识别结果对配准算法中的相对不动点集进行更新，力争所有符合条件的相对不动点均参与配准.最后依据工程知识，使用节点平衡法则对结果做出验证，以保证识别结果的合理性与可靠性.符合节点平衡法则的将直接输出结果；不符合的则继续更新相对不动点集，重新运行配准算法，直至输出结果符合该项准则.其中，随着成功应用案例的不断积累，对不同桥型、不同场景、不同目的下优化后的相对不动点集进行科学归纳，形成不动点集数据库，从而采用深度学习算法实现待测桥梁点云配准时相对不动点集的智能选择.即将基于点云数据的桥梁空间形态识别所需的工程知识转化为经过优化的不动点集数据库.此时，点云配准的关键环节转化为不动点集的智能识别，可进一步提高该方法形态变化识别的准确性与科学性.流程中各环节具体方法将在2.2～2.4节详细说明.

2.2 点云分割与配准

桥梁构件作为桥梁整体的一部分，其构件内部变形常被桥梁整体刚体变形“覆盖”［16］.直接从桥梁整体角度识别构件变形较困难.点云分割可将构件点云从桥梁整体点云中分离，以聚焦构件自身内部变形行为；现阶段已有多位学者提出不同的点云分割算法［17-19］.

本文基于通用点云处理软件CloudCompare 进行分割.首先进行桥梁结构骨架化，即提取桥梁结构不同构件外轮廓；然后根据桥梁骨架识别相应节点，即确定构件界面关键节点；最后利用关键节点将整体点云分割为独立构件点云.

以某一跨主梁点云分析为例，首先沿结构纵向且与桥梁中心线重合构建一条辅助线（见图4）；然后沿该线按某一较小间距批量生成一组正交截面（见图5）；利用该组截面截取桥梁点云，得到一组对应正交云片，即可形成桥梁骨架（见图6）.

图4 辅助线构建Fig.4 Establishment of auxiliary line

图5 正交截面生成Fig.5 Generation of orthogonal sections

图6 桥梁骨架Fig.6 Skeleton of bridge structure

完成桥梁骨架化后，即可在高密度桥梁骨架中直观分辨梁体构件的关键节点，即梁端起止点.图7中a—b间点云则构成单个主梁构件.

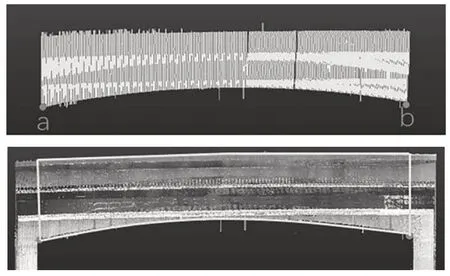
图7 关键节点识别与梁体构件分割Fig.7 Identification of key points and segmentation of bridge girder

同理，在点云骨架中亦可定位桥墩构件关键节点，图8中点c与点d即为桥墩两侧墩梁连接节点，据此可准确分割得到桥墩点云模型.

图8 关键节点识别与桥墩构件分割Fig.8 Identification of key points and segmentation of bridge pier

分割得到各单体构件后，根据结构力学知识及实际工程经验，由于支座提供较大刚度的竖向支撑，梁端竖向挠度应明显小于梁体其他位置；而对于桥墩，墩底侧向变位又应明显小于桥墩其他位置.因此，应用基于工程知识的配准算法时，分别选取梁体端部以及桥墩底部区域作为配准相对不动点，计算点对间空间转换矩阵，完成不同时间点采集的同一构件点云（新旧点云）间的局部配准（见图9）.

图9 点云配准Fig.9 Point cloud registration

2.3 形态变化识别

一旦得到新旧点云空间转换矩阵，将其作用于新点云，即可实现新旧点云坐标系的统一.此时两点云间计算得到的配准残差，即为本次配准后该构件在该时段内所发生的形态变化.通过两点云间对应点间距云图和标尺即可直观且定量得到桥梁构件各位置的形态变化（见图10）.

图10 配准残差Fig.10 Registration residual

一次配准后，将识别结果中未发生位置变化或变化可忽略的、且未参与前次配准的点并入相对不动点集，再进行二次配准，直至无须更新相对不动点集.此时识别结果具备此配准算法下的最高精度.

2.4 识别结果验证

桥梁形态变化与其结构特征紧密相关，即荷载作用下桥梁变形必然遵循一定的力学规则.合乎规则的形态变化识别结果被认为是合理的；反之，违背规则的识别结果必然不能反映真实的形态变化，需要进一步优化配准过程，直至结果合理.

本文推荐采用“桥梁节点平衡准则”来判定识别结果的可靠性，即以识别所得各构件形态变化是否符合桥梁关键节点处力学平衡条件这一准则，判定识别的准确性.如图11 所示，该图为某次配准得到的两跨连续梁主梁与桥墩的形态变化识别结果.根据结构力学知识，桥墩识别出纵向偏移/弯曲，在墩梁固结节点A 处引起图中所示纵向弯矩；而主梁仅识别出整体竖向位移，在墩梁固结节点A 处引起竖向压力.A 处弯矩ΣMA无法达到力学平衡，同时A 处各构件间的结构变形也不连续，因此该形态变化识别结果被判定为不合理.

图11 形态变化识别结果不合理Fig.11 Irrational deformation identification results

图12 为补充相对不动点集后再次配准的结果，从各构件形态变化识别结果可看出，节点B 处同时承受来自桥墩的纵向正弯矩以及来自主梁的纵向负弯矩，恰好可满足ΣMB=0 的力学平衡条件，同时桥墩与主梁变形在B 处均保持连续.因此该形态变化识别结果被判定为可靠.

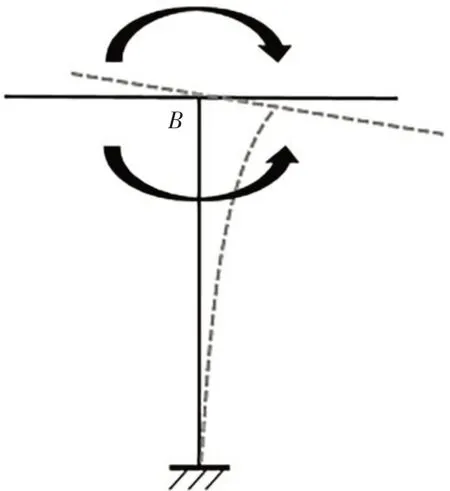
图12 形态变化识别结果合理Fig.12 Rational deformation identification results

合理可靠的形态变化识别结果可直接输出，一旦违背“桥梁节点平衡准则”，则需重新选择参与配准的初始相对不动点集，重复配准直至结果合理.

3 工程应用

3.1 背景桥梁简介

工程应用选择山区某多跨高墩刚构桥（如图13所示）.桥梁全长1 010 m，由左右两幅组成；主桥布置为：六跨预应力混凝土连续刚构（4×120 m）＋连续箱梁（66 m×2），长度为612 m.2～4 号墩为墩梁固结体系，其余桥墩设置盆式橡胶支座；现浇箱梁采用C55 混凝土；预制箱梁、现浇接头与湿接缝等采用C50 混凝土；刚构处主墩采用C55 混凝土，连续梁处主墩采用C40 混凝土，承台与桩基采用C25 混凝土.桥梁曲线部分，其桥墩横向按曲梁径向布置，且左、右幅桥墩在同一条直线上.

图13 背景桥梁Fig.13 Background bridge

根据该桥定检报告，多年运营后该桥多跨主梁腹板与翼缘板均存在明显纵向裂缝；且依据桥面测点高程数据，主梁已发生不同程度的跨中下挠现象.亟须对桥梁空间形态变化进行精准识别并以此评估其安全状态.

3.2 现场激光扫测

研究团队分别于2017 年和2018 年利用三维激光扫描技术两次对该桥进行点云模型的数字采集.由于该桥梁体量庞大，且所处地势复杂，难以仅通过某一个视角获得所有形态信息.为保证数据完整性，确保桥梁各构件关键位置信息不缺失，采取多次扫测结合点云拼接的实施方案，即选取各桥墩底部（近点）、各跨跨中（近点）以及桥梁侧面（远点）分别设站（如图14 所示），若因地形限制导致设站困难，则依据就近原则将三维激光扫描仪临近设置.图15 以“×”示出全部测站位置.

图14 扫测方案Fig.14 Laser scan plan

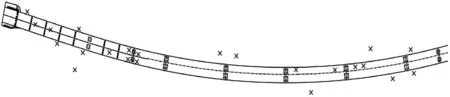
图15 测站位置Fig.15 Locations of scan stations

另外，为确保较好的激光扫描反射效果，激光发射方向与扫测面尽量保持较大夹角，同时反射面避免深色系颜色.事实上，对于常规桥梁，浅色的混凝土表面以及常规涂装的钢结构表面均可保证较好的激光反射效果.

3.3 点云模型处理

三维激光扫测直接获取的点云模型为独立多站源数据，需多站拼接才可得到完整结构点云.图16所示为2017 年与2018 年扫测后经拼接生成的全桥点云模型.

基于桥梁检测报告，对跨中竖向下挠较严重的2～4 跨主梁以及对应桥墩进行重点分析.经过辅助线构建、骨架化、关键点识别与点云分割后，得到各跨主梁与桥墩的单体点云模型（如图17所示）.

图17 单体点云模型Fig.17 Point cloud models for single components

然后针对2017 年与2018 年所采集分割的单体点云模型进行两两配准.配准时，主梁选取梁端区域节点作为相对不动点集；桥墩选取墩底区域节点作为相对不动点集.

3.4 识别结果与分析

配准后每个构件得到独立的空间转换矩阵，用该转换矩阵对待配准点云（2018年数据）进行空间变换，使其与参考点云（2017 年数据）处于同一坐标系下.此时计算两组点云模型中对应点的距离即为该构件在1 年内所发生的形态变化.主梁形态变化识别结果如图18所示.

图18 第1 列为各跨主梁点云的形态变化矢量图.若将其中竖直向上与竖直向下变形的点分别分离，即可得到第2 与第3 列的点云图；图中竖直向上与竖直向下的点云几乎中心对称并分布在梁体对角线的两侧.基于基本力学知识，各跨主梁可被视为已发生不同程度的竖向弯曲与侧向扭转，即处于弯扭耦合状态.图19 进一步绘出各跨主梁的整体弯扭形态，其中“+”表示该区域点云向上位移，“-”表示该区域点云向下位移.也就是说，2017至2018年，除了检测报告指出的跨中弯曲引起的竖向下挠外，还发生了明显的侧向扭转，从而导致主梁处于复杂的弯扭耦合状态.显然，该弯扭耦合的形态变化是传统测量手段无法准确识别的.

图18 主梁形态变化识别结果Fig.18 Change identification of girder deformations

图19 主梁弯扭耦合Fig.19 Coupling of bending and torsion of girders

图20为桥墩构件在1年内所发生的形态变化识别结果.从位移矢量图中可以看出，所有桥墩的形态变化均表现出相似特性，即越靠近墩底，变形越小；越靠近墩顶，变形越大；且均同时发生横桥向与纵桥向的水平变形/侧弯.

图20 桥墩形态变化识别结果（双柱墩）Fig.20 Change identification of pier deformations

3.5 结果验证

利用结构工程知识判断上述识别结果是否可靠.首先从横桥向分析主梁与桥墩的变形行为，如图21 所示，桥墩发生横桥向位移/侧弯的同时，其相连主梁发生轴向扭转.此时，主梁扭转产生的扭矩与桥墩侧弯产生的弯矩相互平衡，即墩梁节点处横桥向满足节点平衡条件，且变形连续，横桥向完成其可靠性验证.

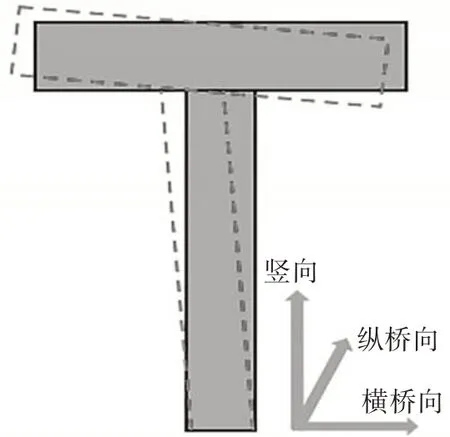
图21 横桥向验证Fig.21 Verification along transverse direction

另外，对于连续梁桥，还可利用竖平面曲线分析桥梁整体形态变化的连续情况.如图22所示，第2、4跨主梁向下竖弯，第3 跨向上竖弯，且在桥墩处竖弯变形连续；同时两桥墩均向第3 跨方向发生纵桥向侧弯，即墩梁节点处纵桥向变形连续，且满足节点平衡条件，纵桥向完成其可靠性验证.

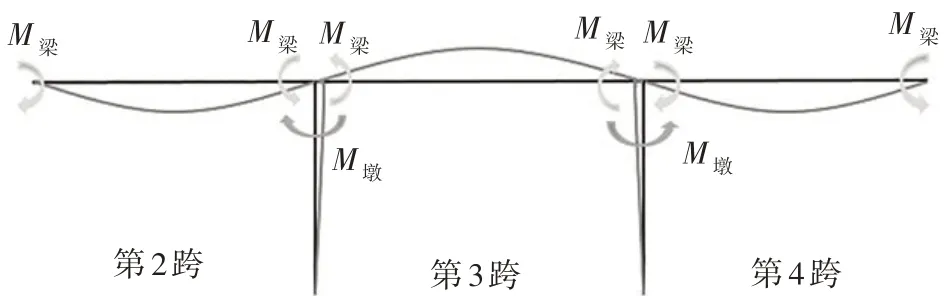
图22 纵桥向验证Fig.22 Verification along longitudinal direction

4 结论

1）提出一种基于工程知识的点云配准算法，其基于传统ICP 配准算法，根据实际工程知识，仅选取相对不动点集参与配准.该算法可同时提高配准效率与精度.

2）提出一种基于点云数据与工程知识的桥梁形态变化识别方法.首先利用结构骨架化对桥梁构件进行单体分割，然后基于工程知识对配准相对不动点集进行优化，进而针对新旧构件点云配准，得到该时段内构件的形态变化，最后利用结构工程知识验证其可靠性.

3）将所提出方法应用于实际工程，得到背景桥梁各关键构件一年内发生的形态变化，并利用“桥梁节点平衡准则”，包括节点力学平衡与变形连续，验证其识别结果的可靠性.

4）基于点云数据与工程知识的桥梁形态变化识别方法为桥梁检测/监测与评估提供了新思路与新技术，可精准分析桥梁结构整体变形与构件局部形态变化，并以此评估桥梁隐性失效.

5）该项技术适用于山区桥梁、跨江桥梁、市政涉水桥梁等多种桥梁，还可用于智慧建造、施工监控、养护评估等多个环节；但具体应用时，仍需根据结构布置、构件形式、桥址环境等因素进行扫描专项设计与进一步的数据处理方法优化.