一种考虑低压侧直供潜力的输配电网规划方法研究

郭露方，张宝丹，吴广大，姜志筠，包鹏宇，吴国鼎，郑子健，胡 钋

（1.武汉大学电气与自动化学院，湖北武汉 430072；2.云南开放大学机电工程学院，云南昆明 650223）

0 引言

随着中国经济发展进入新发展阶段，电力负荷需求不断增加。为了满足日益增长的负荷需求，必须加快电网建设进度，不断扩大电力系统的规模，确保电力可靠供应。为避免大规模重复建设和投资浪费，电网规划必须解决优化电网结构[1-2]、合理平衡区域负荷和协调220 kV 与110 kV 变电站布点关系等问题。

传统的送电方式[3-4]大都采用从220 kV 降压到110 kV 再降压到35 kV，10 kV 或6 kV 的送电方式，也有220 kV 变电站采用三卷变压器10 kV 低压侧直接向负荷供电（简称10 kV 直供负荷）。由于变电站的位置、容量及供电范围关系到待规划区域电网的网架结构和空间布局，在满足一定的容载比条件下，在规划过程中220 kV 变压器低压侧直供负荷大小，会直接影响110 kV 变电站的规模，进而影响整个110 kV 站点布局和网架结构，同时配电网规划结果也会影响上级输电网规划结果，因此，在规划过程中考虑上级电网的直供潜力，输电网和配电网在规划建设时相互配合，可减少不必要的重复降压，提升投资经济效益，提高设备利用率。

输电网与配电网规划问题从数学角度出发，可以视为一个包含多个约束条件的非线性混合整数规划问题[5-7]，具有多目标、非线性等特点。文献[8]以系统运行成本和投资建设成本为经济性目标，并加以最小缺电成本的安全性目标，给出了泛函形式的电网规划模型。文献[9]根据网络结构熵理论在输电网扩展规划中考虑负荷均衡性从而达到提高电网运行可靠性和经济性的目的。文献[10]输电网规划中，引入不确定理论使规划方案能适应不确定因素带来的影响。这些输电网规划过程中考虑了多种影响因素，但未考虑与下级配电网的配合，因此无法保证未来配电系统的供电可靠。文献[11]基于供电变电站和高压线路通道N-1 供电安全性最大化，同时考虑到高压联络线路费用的最小化，提出了基于供电分区优化的高压配电网目标网架规划优化模型和方法。文献[12]通过年最小收入计算，对电网改造方案可靠性和经济性进行评估，将可靠性和经济性统一考虑并应用到城市配电网规划中。文献[13]采用层次空间推理的方法，提出了城市配电网多级网格划分手段，从而使配电网规划更加精细。这些配电网规划研究过程中没有考虑与输电网之间的协调，可能导致最终配电网规划方案与输电网之间的负荷转移路径不足，影响整个电网运行的整体可靠性和经济效益。文献[14]从全局角度对系统进行优化，以输配系统整体供电成本最低为目标函数，建立了输配两级电网基础调度模型。文献[15]从技术和经济效益上分析在变压器低压侧采用大电流设备提升10 kV 低压侧的直供能力，为220 kV 变电站的规划建提供新的参考。文献[16]提出一种优化的低压侧接线方式，优化后的接线方式能够提高供电可靠性，具有扩建灵活、土地资源利用率高的特点。目前输配电网联动的研究[17-20]主要集中在运行调度的匹配上，并且有关直供能力的研究多集中在理论技术分析和供电可靠性上，对于规划层面上的输电网与配电网在布局和规模上的相互匹配以及直供负荷对电网结构和资源配置结果的影响研究较少。

本文通过充分发掘低压侧直供潜力，在规划过程中考虑输电网与配电网的网间匹配，综合考虑上下级输配电网之间的连接关系，合理配置各个等级电网的变电站及线路资源，建立输配电网联动规划模型，以实现电网规划方案具有较低的建设投资、较高的设备利用率以及合理的安全裕度，优化输电网与配电网规划的目的。此外，由于现代启发式算法[21-27]在求解电网规划问题时通常存在计算效率不高与易陷于局部最优等问题，故而采用群体最优值交叉操作的量子粒子群算法（Quantum Particle Swarm Optimization，CR-QPSO）对其进行求解，以提高全局搜索能力，在寻优过程中建立粒子信息记忆集，有效解决了现代启发式算法在求解电网规划问题时存在的效率不高及未成熟收敛等问题，提高了收敛速度。

1 考虑直供能力的配电网规模估算模型

由于考虑变压器低压侧直供负荷能力，负荷的供电来源不再是单一维度，呈现出不同电压等级序列的特点。对于220/110/10 kV 电压等级序列，110 kV 配电网的电源来源为上级220 kV 输电网，由于220 kV 变电站可采用三卷变压器10 kV 低压侧直接向负荷供电的方式，10 kV 配电网的电源来源包括上级220 kV 输电网和上级110 kV 配电网。对于1个变电站内总容量为720 MVA 的3 台主变压器，直供侧设置3×10=30 个出线间隔，每个出线间隔负荷在4～6 MW 范围之内，则直供侧的直供能力与1 个110 kV 站点的供电能力相匹配。主变低压侧直供负荷占下网负荷的比例不同，就会在规划层面直接影响配电网站点规模和负荷分布情况。

考虑变压器低压侧直供负荷能力时，主变下网负荷包括2 类负荷即常规负荷lR和直供负荷lD，其满足集合关系，即：

式中：LR为常规负荷集合；LD为直供负荷集合；L为2 类负荷汇总形成规划区总负荷集合；M，N分别为常规负荷和直供负荷个数。

考虑变电站直供占比时，220 kV 和110 kV 站点的规模N220，N110估算分别为：

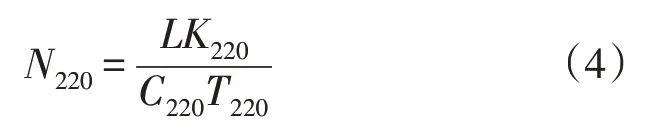
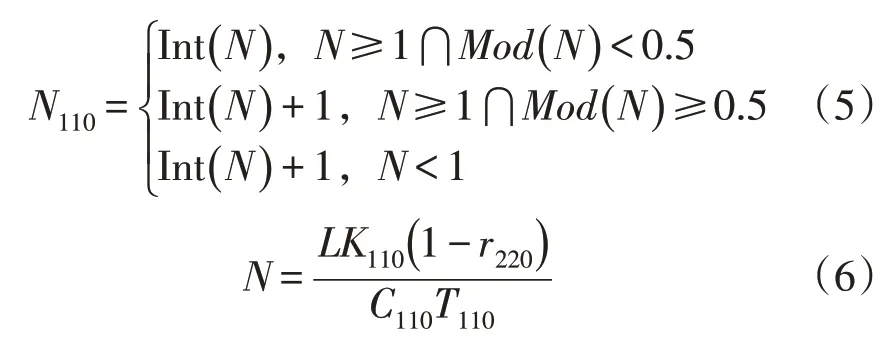
式中：K220，K110分别为220 kV 和110 kV 变电站的容载比；C220，C110分别为220 kV 和110 kV 变电站的主变容量；T220，T110分别为220 kV 和110 kV 变电站站内主变台数；r220为220 kV 变电站的直供占比。

2 输配电网规划模型及其分解

输电网和配电网的规划模型可以表示为：

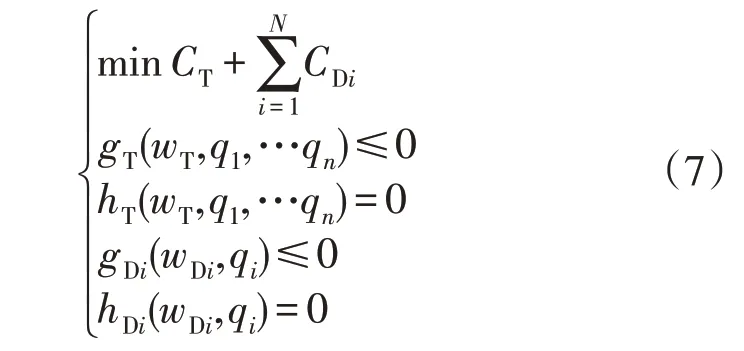
式中：i=1,2,…,N为与输电网连接的第i个配电网；CT和CD分别为输电网和各配电网的目标函数；gT和hT分别为输电网侧不等式约束和等式约束；gD和hD分别为配电网侧不等式约束和等式约束；wT和wD分别为输电网和配电网的内部网络参数；q为输电网与配电网的功率传递信息。

为了更好地满足输电网侧和配电网侧不同电压等级间的规划调度需求，建立考虑上级输电网和下级配电网的变电站与网架联动规划模型，该模型能够综合考虑上下级输配电网之间的连接关系，考虑上级电网的直供潜力，合理配置各个等级电网的变电站及线路资源。

综合考虑变电站与网架的输配电网联动规划，随机确定配电网和输电网的待选变电站建成状态，根据已有变电站和新建变电站确定直供范围，选择直供负荷，建立直供负荷集和常规负荷集，计算直供占比并进行输配电网的规模估算，若发生变化，更新输电网和配电网的规模，重复上述规划步骤；否则，根据已选的输电网变电站和配电网变电站，进行网架规划，最终输出输电网和配电网的整体规划方案。

2.1 变电站规划

变电站规划模型采用经济性评估指标即输电网侧新增变电站规划投资成本和配电网侧新增变电站规划投资成本等，模型以投资成本CS最低作为目标函数。

1）目标函数。变电站规划模型目标函数可表示为：

式中：CTS为输电网侧变电站规划投资成本；CDS为配电网侧变电站规划投资成本。

CTS，CDS可表示为：

式中：YTS，YDS分别为输电网变电站运行周期和配电网变电站运行周期；NTS，NDS分别为输电网待选变电站个数和配电网待选变电站个数；分别为为输电网变电站和配电网变电站建设费用；Bij值为1 时表示新建站点，为0 时表示不新建站点；d为贴现率。

2）直供范围划分。参考输电网变电站与已选配电网变电站的距离，取其最小距离的1/2 作为输电网变电站直供半径，划分直供范围，并从中随机选取负荷进入直供负荷集，由上级输电网直供，其余负荷进入常规负荷集，由配电网变电站供应。

2.2 网架规划

2.2.1 输电网侧规划模型

输电网侧规划模型采用经济性评估指标即输电网侧新增线路规划投资成本和运行成本等，模型以综合成本CT、新增输电线路年成本和年运行成本最低作为目标函数。

1）目标函数。输电网规划模型目标函数为：

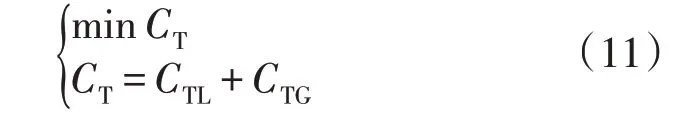
式中：CTL为输电线路投资成本；CTG为发电机组运行成本。

发电机组运行成本CTG经分段线性化后为：

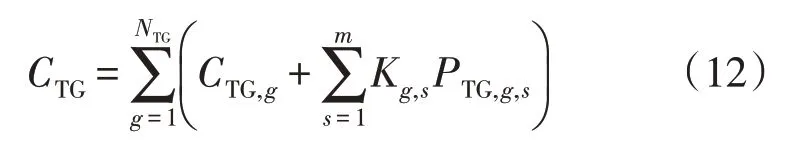
式中：NTG为机组台数；m为总分段数；Kg,s为第g台机组分段线性化之后第s分段煤耗系数；PTG,g,s为第s分段出力；CTG,g为第g台机组最小出力运行时的煤耗成本。

输电线路投资成本CTL为：

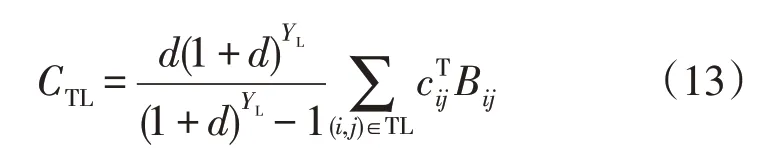
式中：TL为新建线路集；为输电网节点(i,j)间线路的建设费用；YL为线路运行周期。

2）约束条件。输电网规划模型满足以下4 个约束。

网络的潮流约束为：

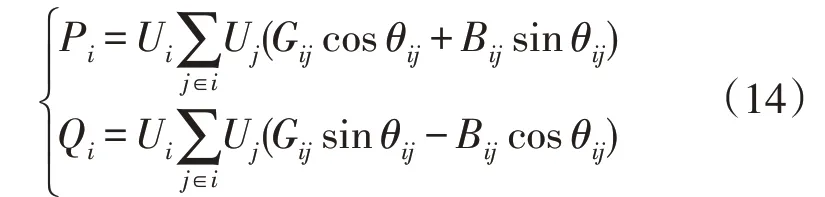
式中：Pi和Qi分别为节点i的有功和无功注入量；Gij和Bij分别为节点导纳矩阵的实部和虚部；θij为节点i和j之间的相角差。

系统安全约束为：

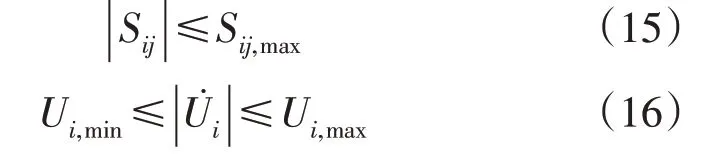
式中：Sij,max为线路容量限值；Ui,max和Ui,min为节点i的电压上、下限值。

火电机组组出力上、下限约束为：

2.2.2 配电网侧规划模型

配电网侧规划模型包括线路投资总成本和配电网运行总成本，模型以配电网年综合费用CD最低为目标函数。

1）目标函数。配电网规划模型目标函数可表示为：

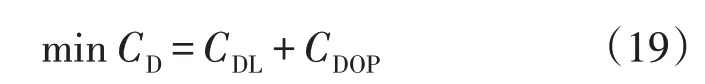
式中：CDL为线路投资总成本；CDOP为运行总成本。

规划建设总成本CDL可表示为：

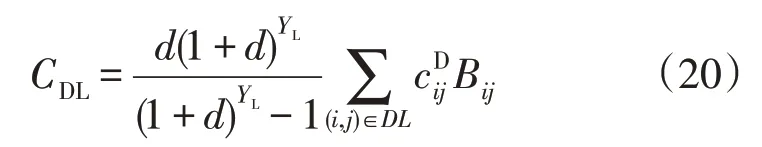
运行总成本CDOP包括等效电源出力成本CDG和网损成本Closs，可表示为：

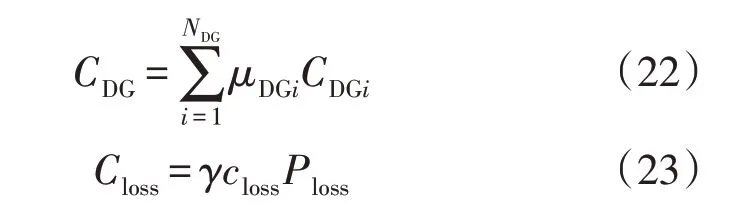
式中：μDGi为成本系数；γ为网损成本系数；closs为单位网损费用；Ploss为网损功率。

2）约束条件。配电网与输电网潮流约束条件一致。

配电网侧节点电压约束为：

线路传输载流量约束为：

式中：Im，分别为第k条线路上的电流大小和电流上限值。

配电网在建设和布局上的约束有系统连通性约束和辐射状约束。

2.2.3 输配电网规划模型分解

由于对网架规划模型直接求解计算量太大，运算比较复杂，因此根据输电网与配电网在其连接处的耦合关系即输电网与配电网连接处功率保持一致，进行信息交互。当规划过程中考虑上级电网直供能力时，上级输电网节点作为等效电源向下级传输的功率包括下级配电网等效负荷和直供负荷，于是，输电网与配电网在连接处传递的信息包括连接处配电网等效负荷信息和直供负荷信息。为此，引入反馈变量f=(f1,f2,…,fN)T，表示从配电网侧反馈至连接处的上级电网直供负荷，从配电网角度向上级的传输功率表示为Pd=(Pd1,Pd2,…,PdN)T，从输电网角度向下级的传输功率表示为Pt=(Pt1,Pt2,…,PtN)T，满足式（26）关系，即：

因此建立差值约束条件，即：

根据拉格朗日罚函数形式将该约束松弛至目标函数中，得到输配电网规划目标函数为：

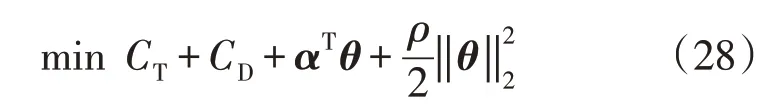
式中：α为乘子变量；ρ为惩罚因子。

输配电网规划目标函数的耦合约束可以将输配电网规划问题分解为输电网规划和配电网规划2个子优化问题，2 个子问题相互迭代，实现分布式求解，输出最优结果。

输电网侧和配电网侧的模型分别为：

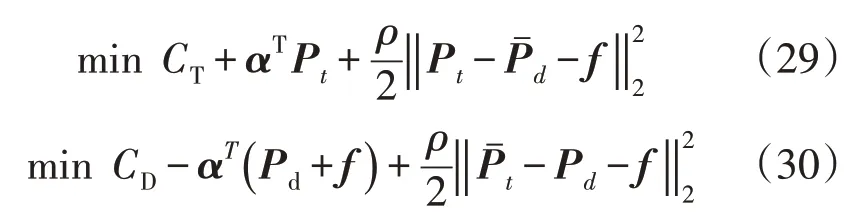
式中：为配电网侧向上级的传输功率在迭代过程中为确定值；为输电网侧向下级的传输功率，在迭代过程中为确定值。

求解流程为：（1）设置内、外层最大迭代次数m，k，模型参数初始化；（2）在输电网规划问题中，从配电网角度向上级的传输功率为Pd作为已知参数，Pt作为优化变量求解，求解结果作为已知参数传递到配电网规划问题进行求解；（3）进行内层迭代收敛判断：

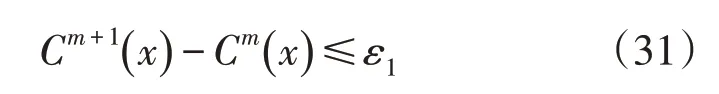
式中：C(x)为输配电网规划目标函数；ε1为内层收敛精度。

若式（31）满足，进行下一步，否则返回流程（2）；（4）进行外层迭代收敛判断：

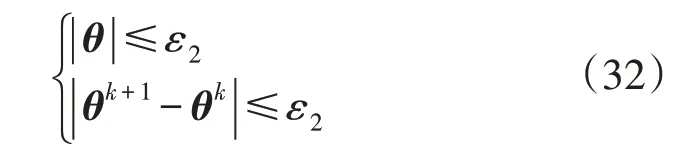
式中：ε2为外层收敛精度。

若式（32）满足，输出结果，否则进行下一步；（5）系数更新，返回流程（2）。

α的更新公式为：

3 基于CR-QPSO算法的模型求解

量子粒子群算法可以表述为：定义1 个D维求解域，种群个体数为n，即X=(X1,X2,…,Xi,…,Xn)，对应表示n种规划方案，每个个体均对应1 个D维解，即第i个种群个体为Xi=[xi1,xi2,…,xiD]T，通过所设置的适应度函数，计算个体粒子的适应度值，个体极值也为1 个D维解Pi=[Pi1,Pi2,…,PiD]T，表示第i个种群个体迭代过程中最优的规划方案，同理群体极值为Pg=[Pg1,Pg2,…,PgD]T表示整个种群在迭代过程中最优的规划方案。

根据个体极值和群体极值的状态信息，个体粒子采用蒙特卡洛法模拟运动状态，通过种群迭代过程不断更新自身位置，更新公式为：

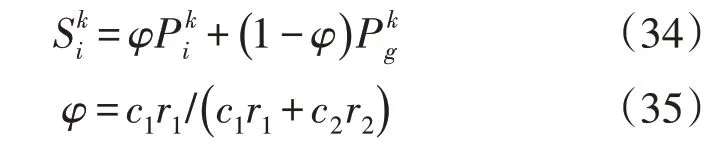
式中：i=1,2,…,n；k为迭代次数；为第k次迭代时第i个粒子根据个体极限和群体极限产生的随机位置；φ为[0，1]内随机数；c1和c2分别称为自身认知因子和社会学习因子，均为正数；r1和r2均为区间[0,1]内随机数。

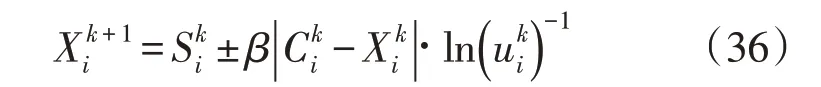
式中：β为收缩扩张系数；为第k次迭代时粒子历史最优位置均值；为0-1 均匀分布随机数；为第k次迭代时第i个粒子的状态信息。

整体规划方案求解流程如图1 所示。

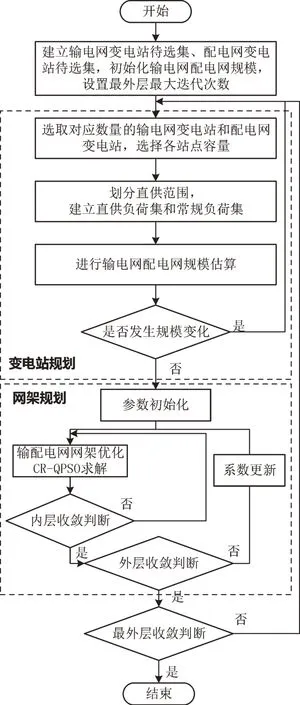
图1 整体规划方案求解流程Fig.1 Overall planning solution process

在整体规划方案求解流程中，最外层循环包括变电站规划和网架规划，变电站规划求解包括变电站选取状态和容量，其中只有1 层循环结构；网架规划求解包括线路建设状态，采取分布式求解，其中有内层和外层2 层循环结构。

此外，为增加迭代后期种群粒子跳出局部最优解的能力和求解速度，对量子粒子群算法进行2 个改进。

1）君主交叉拓展最优集。为了提高跳出局部最优解的能力，利用种群内的最优粒子，用最优粒子作为君主粒子，并随机生成交叉位点，然后将君主粒子与种群内次优粒子进行交叉，产生1 个新粒子，将该粒子与君主粒子、次优粒子组成最优集。在种群迭代过程中粒子更新位置时将从最优集中随机选择最优粒子进行自身位置更新。

2）建立粒子记忆集。为了提高求解速度，在种群迭代过程中记忆所有不满足约束条件的粒子信息，并将其保存至粒子记忆集，若在后续迭代过程中该粒子信息属于记忆集，则直接进行下一次寻优，不再进行约束判断，从而加快寻优速度。

4 算例分析

某市待规划区域占地面积75 km2，包括39 个负荷点，总负荷815.5 MW，15 个可选下级配电网变电站，4 个可选上级输电网变电站，220 kV 变电站容量选择为2×240 MVA，110 kV 变电站容量选择为2×50 MVA，参考国家电网公司输变电工程多维立体参考价，220 kV 变电站建设成本为9 890 万元，110 kV变电站建设成本分别为2 911 万元。电力线路均为双回线，输电网侧线路315 万元/km，配电网侧线路149 万元/km。等效机组出力运行参数设置a=0.02元（/MW）2h，b=20 元/MWh，网损成本为0.45 元/kWh，规划成本设置资金贴现率为5%，资金回收周期为20 a。

整体规划方案求解中，变电站规划过程中220 kV变电站容载比通常设置在1.6～1.9 之间，本文设置容载比应大于1.6，不超过2，110 kV 变电站容载比通常设置在1.8～2.1 之间，本文设置容载比应大于1.8，不超过2.1。最外层最大迭代次数设置为50，初始输电网和配电网变电站规模选取为4，15。网架规划过程中，内外层最大迭代次数为20，50。拉格朗日乘子初始设置为0.8，惩罚因子设置为1，CR-QPSO 求解中初始参数设置：最大迭代次数为50，种群规模为30，认知因子取0.5，社会学习因子取0.5，收缩扩张系数取1.2，收敛系数取0.01。输电网规划过程中潮流计算采取最优潮流方式，即在满足所有运行约束条件下得到发电成本达到最优值下的潮流分布。

4.1 规划拓扑对比

为了比较考虑直供负荷对规划结果的影响，将有无直供负荷的规划结果进行对比。当规划过程中考虑直供负荷因素时求解得到规划结果，输电网规划方案如图2 所示，配电网规划方案如图3 所示。

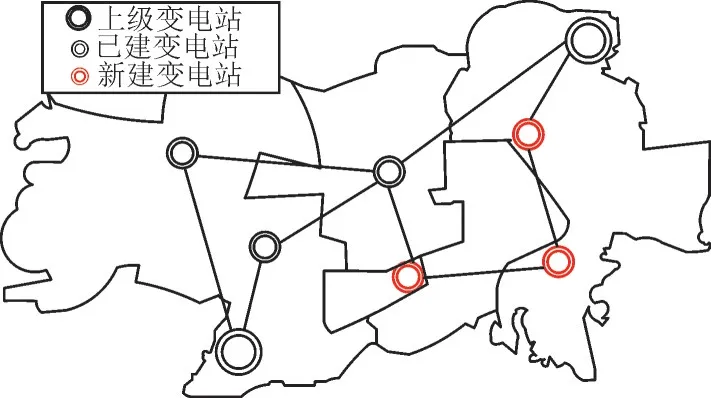
图2 有直供负荷情况下输电网规划拓扑图Fig.2 Planned topology diagram of transmission network with direct supply load

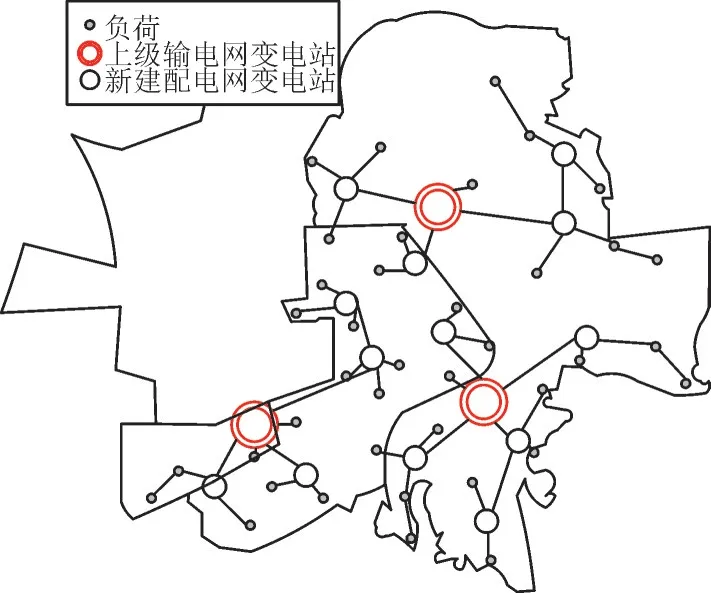
图3 有直供负荷情况下配电网规划拓扑图Fig.3 Planned topology diagram of distribution network with direct supply load

在规划过程中考虑直供负荷时，输电网侧新增了3 个站点，直供负荷集包括4 个负荷，负荷值合计58.7 MW，配电网侧新增了13 个站点，常规负荷集包括35 个负荷，负荷值合计756.9 MW。当不考虑直供负荷时，输电网规划结果无变化，配电网规划方案如图4 所示。配电网侧常规负荷集包括所有负荷，新增了15 个站点，站点规模大于考虑直供负荷时的站点规模。

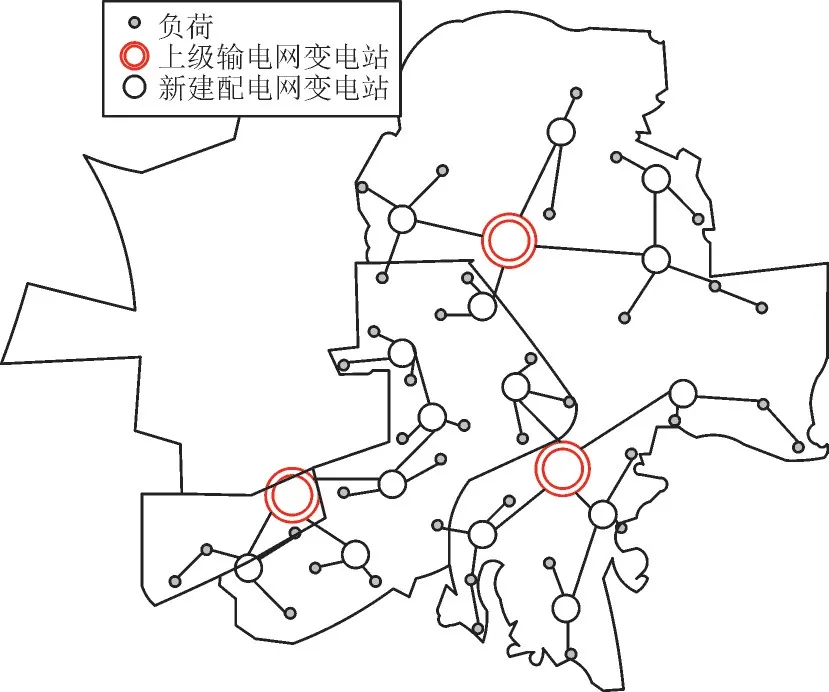
图4 无直供负荷情况下配电网规划拓扑图Fig.4 Planned topology diagram of distribution network without direct supply load

4.2 规划方案经济性对比

采用带直供负荷情况下的规划结果，将输电网与配电网规划方案进行经济性对比，结果如表1 所示。

由表1 可知，考虑直供负荷时输电网侧总成本中运行成本占比较大，主要来源于发电机组发电运行成本。配电网侧由于站点规模较大，线路建设较多，因此规划建设成本和线路投资成本在总成本中的比重上升，占比为31.9%。不考虑直供负荷时配电网侧规划建设成本和线路投资成本在配电网侧总成本中的占比为34.4%，相较于考虑直供负荷时有所增加。通过对比可知，当输配电网规划过程考虑直供负荷时，规划建设成本和线路投资成本均有所减少，相较于不考虑直供负荷时的规划建设成本减少比例达到13.3%，总规划成本减少主要来源于规划过程考虑直供负荷导致配电网侧站点规模变化，此外网架的优化使得电网运行成本也有所降低。通过输配电网规划过程考虑直供负荷因素，增加了可选择规划方案的范围，改善电网建设成本，从而使电网规划方案得到进一步优化。

4.3 容量可选规划方案对比

当110 kV 变电站容量选择为2×50 MVA 和2×63 MVA 时，110 kV 变电站建设成本分别为2 911万元和3 205 万元，同时考虑直供负荷对规划结果的影响，得到规划方案，输电网规划方案如图5 所示，配电网规划方案如图6 所示，并与4.2 节容量固定情况下的规划方案进行对比。

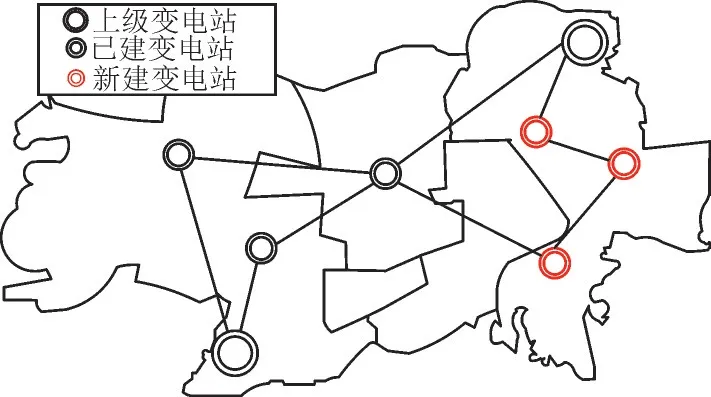
图5 容量可选情况下输电网规划拓扑图Fig.5 Planned topology diagram of transmission network with optional capacity

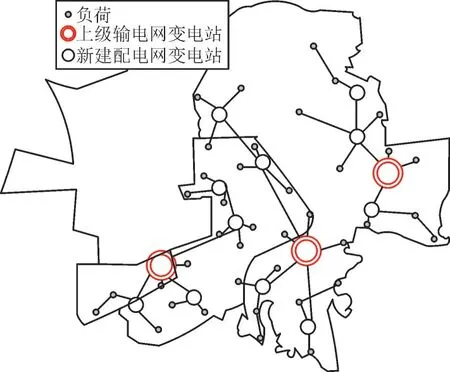
图6 容量可选情况下配电网规划拓扑图Fig.6 Planned topology diagram of distribution network with optional capacity

当在规划过程中110 kV 变电站容量可选时，此时输电网侧的站点选择发生了变化，由于配电网侧容量选择方案的差异，导致配电网的站点规模和输电网侧直供负荷的选择均发生变化，即使输电网侧投资成本有所增加，但使整体规划方案更优。

配电网侧的站点分布进行进一步优化，此时直供负荷集包括7 个负荷，负荷值合计106.3 MW，配电网侧新增了11 个站点，容量选择为2×50 MVA 的有4 个，容量选择为2×63 MVA 的有7 个，常规负荷集包括32 个负荷，负荷值合计708.7 MW。

将容量可选规划方案与容量固定规划方案进行对比分析，结果如表2 所示。

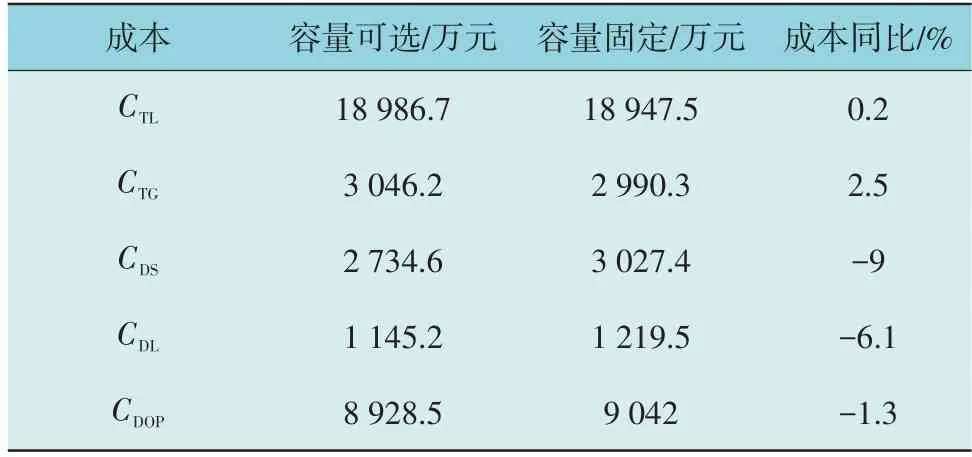
表2 输配电网规划方案经济性对比Table 2 Economic comparison of transmission and distribution network planning

由表2 可知，虽然输电网侧投资成本同比增加2.5%，但由于变电站所选容量的进一步优化和配电网侧110 kV 变电站布局和规模的改变，导致配电网侧规划建设成本同比减少9%，线路建设成本同比减少6.1%，综合成本相较于固定容量情况下减少，提升规划经济效益，整体规划方案得到进一步优化。

5 结论

本文提出了一种考虑变压器低压侧直供负荷的电网规划方法，得出主要结论如下：

1）通过建立考虑变压器直供占比的电网规模估算模型，并将其纳入到输配电网联动规划中，可以充分利用变压器低压侧直供能力，优化变电站投资建设。

2）通过引入输电网与配电网的反馈变量，实现输配电网连接处的运行匹配。将整体规划模型分解为输电网规划模型和配电网规划模型，优化求解。

3）采用群体最优值交叉操作的CR-QPSO 算法求解模型，扩大了搜索范围，提高了非线性优化问题的寻优能力，此外，通过建立粒子记忆集，避免了粒子的无效更新，提高了模型求解速度。

4）考虑直供负荷进行输配电网规划可合理控制总体投资，优化上下级电网的站点规模，避免重复降压，节省电网投资成本，提高经济效益。