基于小口径弹药的柔性安保机构设计

刘演龙，陶伟琪，陈云友

(1.海装广州局， 广州 510000； 2.重庆长安工业(集团)有限责任公司， 重庆 401120)

1 引言

微电子技术的发展，推动着小口径弹药引信不断走向小型化、集成化和智能化，现代武器装备对弹药设计，要求在弹药有限体积内尽可能增加炸药装药量，以提高其毁伤效能，这就进一步压缩了引信空间。采用MEMS技术可以减小引信安全系统体积，使得引信有更多的空间可以容纳其他传感装置，有效实现引信小型化，增大弹丸装药量、降低生产成本，提高弹药的精度和杀伤力，快速促进智能、灵巧型弹药的发展。现在，MEMS在引信中的应用已经相当广泛。其中，美国MK19 40 mm枪榴弹、MkII 25 mm空爆弹应用的起爆开关微引信系统都是MEMS集成应用于引信的典型代表。而MEMS安全系统结构多为近似平面结构，该系统能在高动态环境下，感知过载并实现结构运动，确保系统安全。早在2002年，Robinson等就开始着手研究MEMS安全系统，并在2005年完成改进设计，该装置在一定的回摆和旋转加速度驱动下有着良好的性能，但因尺寸较大，实际应用受限。2004年，美国海军水面作战中心(Naval Surface Warfare Center)展示了可用作引信安保机构集成化冲击传感器的MEMS冲击开关，该开关无需电源驱动，在感受到冲击加速度高于预设阈值时即可可靠锁定为闭合状态。其后，Steven和Ostrow等，分别在2006年和2012年利用电热技术驱动安全系统，通过表面微加工技术成功地将其尺寸降至毫米级。但这2个团队设计的安全系统都因结构强度低，在高过载条件下可靠性差，引信使用失效率高。经过近几年的发展，2015年Hu T等完成了由4个电热执行器和推进剂组成的可移动结构电热安全系统研制和试验，使得失效率大幅降低。为了提高安全保险系统的可靠性，他们同样引入了互锁机构，成功地将芯片尺寸减小到8 mm×8 mm×0.5 mm，但未能与点火装置结合，导致S&A系统并不完整。本文针对现有的MEMS安全系统结构，开展了针对柔性材料在高动态环境中的响应机制研究，对其进行了理论分析和模型建立。通过COMSOL有限元分析软件对结构设计、材料选型等进行理论计算和仿真建模，得到优化的安全系统结构，并提高柔性安全系统作用可靠性。

2 MEMS系统工作原理

以垂直于弹轴的MEMS悬臂梁式后坐保险机构为例，根据设计要求，后坐保险机构在柔性安全系统中承担着区别正常发射和意外跌落2种环境条件下的不同功能，确保引信在跌落过程中不被触发而在射击条件下可靠解险。设定各器件符合胡克定律，悬臂梁式后坐保险机构不同于传统的单片式设计，传爆序列形成一条直线，可节省传递过程的爆轰能量。其基本运动模型可以等效于弹簧质量阻尼系统，如图1(a)、(b)所示。由于质量块的质量远大于弹簧的质量，同时阻尼力远小于系统工作时的惯性力，为简化分析过程，可忽略弹簧的质量与阻尼对系统响应的影响，将加速度环境下的后坐保险机构等效为一个无阻尼单自由度受迫振动系统，简化后的物理模型如图1(c)。

为了使设计得到的后坐保险装置满足要求，需满足跌落环境下最大的响应位移小于正常发射环境下最小的响应位移。根据上述结论作图，如图2。由图2可见4 ms脉宽下正常发射位移响应曲线与0.15 ms脉宽下跌落位移曲线。

从图2中可以看出，当系统固有角频率较低时，系统正常发射的最小响应位移随系统固有角频率的增加急剧减小，之后随着固有角频率的增加几乎保持不变；但系统跌落时最大响应位移始终随系统固有角频率的增加而缓慢减小，由此证明位移对系统固有角频率不敏感。

由两条曲线的交点坐标可知，在系统固有角频率较小(小于6 276.12 rad/s)时，后坐保险机构在发射环境条件下的最小位移始终大于跌落环境下可能出现的最大位移。

图1 安保机构物理模型示意图

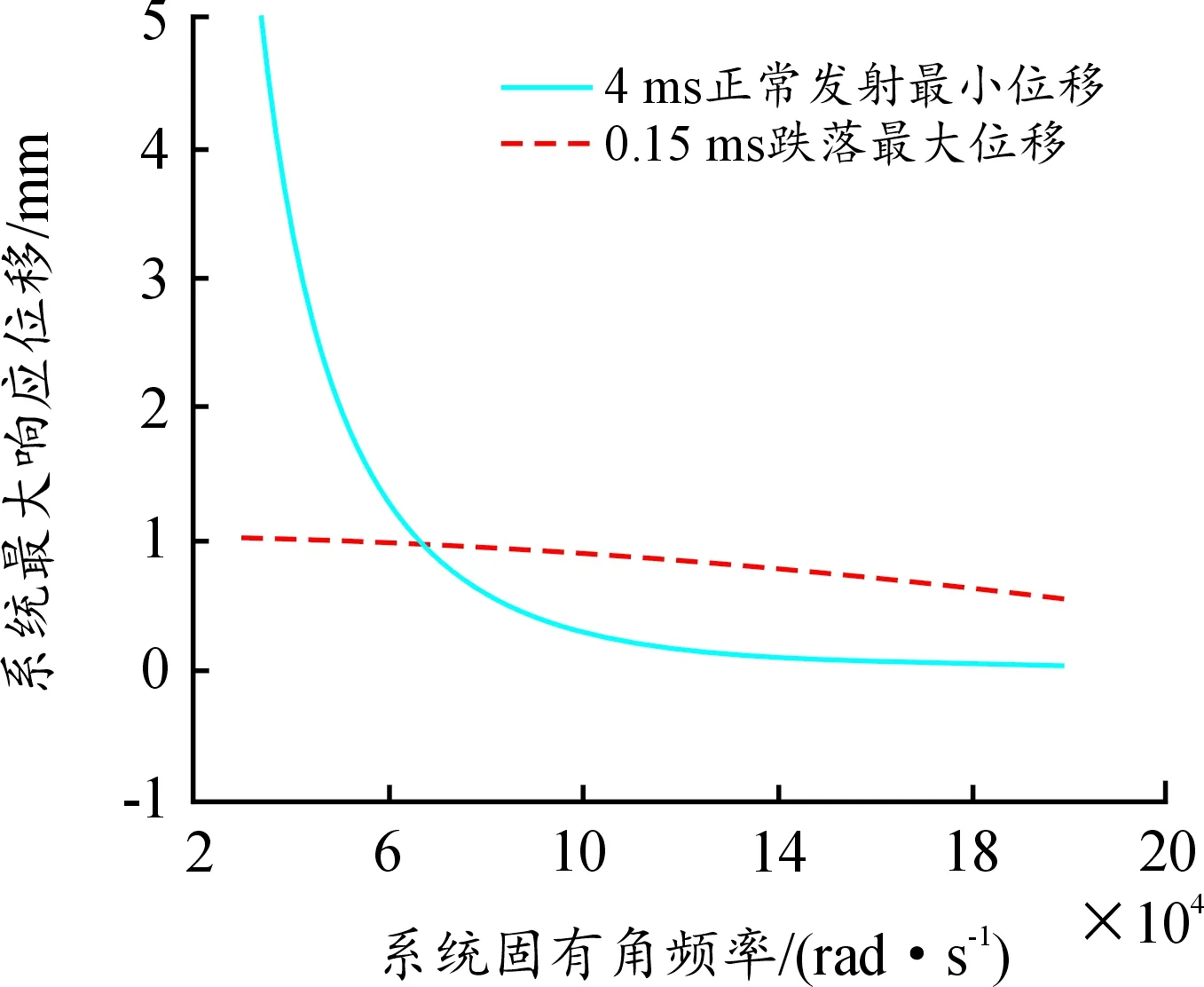
图2 跌落环境下最大的响应位移曲线和正常发射环境下最小的响应位移曲线

3 仿真分析

后坐保险机构模型见图3，根据理论分析得出，若后坐保险机构的悬臂梁固有频率小于6 276.12 rad/s时，后坐保险机构的最低发射条件下的位移响应始终大于跌落环境下可能出现的最大系统位移。由于柔性材料的特点，柔性悬臂梁的固有频率较小，所以较于刚性悬臂梁可以极大地缩小后坐保险系统所占用的体积。

根据理论分析满足的固有频率，建立悬臂梁后坐安全机构的实体模型，并对悬臂梁的尺寸进行了初步选择：长2 mm，宽0.8 mm，厚0.6 mm。该设计尺寸理论上满足要求。隔爆滑块厚度0.8 mm，即悬臂梁与隔爆滑块重叠处形变量大于0.8 mm，即可视为保险稳定解除。

图3 后坐保险机构模型示意图

意外跌落时，分别选取0.1 ms,15 000以及0.15 ms,15 000进行瞬态动力学仿真，得到悬臂梁最远端点A处的位移随时间的变化趋势如图4所示。由图可知，0.1 ms,15 000加速度的最大位移为0.48 mm，而0.15 ms,15 000的最大位移达到了1.25 mm。这证明了理论分析所得的结论：在意外跌落时，对于固有频率一致的器件，加速度脉宽越大，后坐保险机构的位移越大。

图4 悬臂梁最远端点A处的位移响应曲线

对于脉宽为0.15 ms的加速度，其最远端的最大位移为1.25 mm。由于悬臂梁与隔爆滑块重叠区域为悬臂梁长度的0.6倍，因此重叠末端的最大位移应小于最远端A点位移的一半，约为0.5 mm(如图5)。此时隔爆滑块依然被卡住。

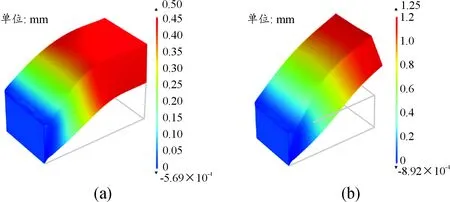
图5 15 000g跌落加速度下后坐保险系统的位移云图

由PDMS的物理性质可知，其拉伸强度为2.24 MPa，跌落时应力云图如图6。跌落状态下最大应力出现在悬臂梁后坐保险机构的固定端，为0.8 MPa，远小于PDMS材料的极限拉应力。在意外施加的跌落加速度后，由于柔性材料的弹性影响，悬臂梁会很快回复到初始状态。此时后坐保险系统工作正常，保证了跌落状态下引信的安全状态，形成稳固的第一道保险。

图6 15 000g跌落加速度下后坐保险系统的应力云图

而在正常发射时，选取4 ms,12 000和6 ms,12 000两种发射加速度进行仿真。其位移响应曲线如图7，在加速度达到最大值(即2 ms、3 ms)前，脉宽越大，悬臂卡锁的位移越小。由图7可知，4 ms、12 000加速度的最大位移为5.65 m，6 ms、12 000加速度的最大位移为5.04 m。在1 ms时间后，悬臂梁位移距离均超过2 mm，此时后坐保险机构稳定解锁，隔爆滑块不再受悬臂梁卡锁的固定而开始在离心力作用下下滑，第一道保险解除。

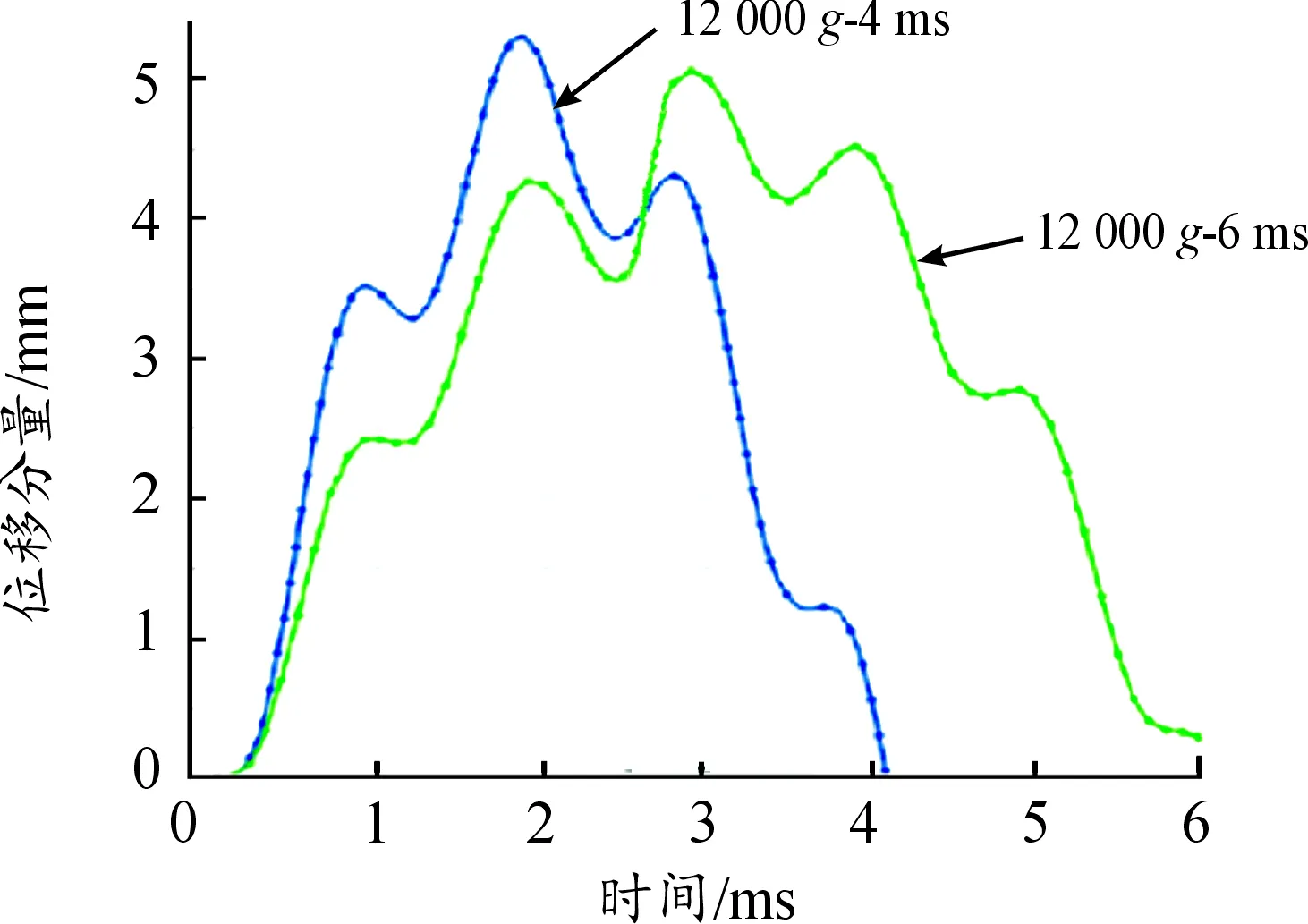
图7 正常发射时悬臂梁最远端的位移响应曲线

当位移达到最大时，后坐保险机构所受的应力如图8所示。从理论分析的结果可知，仿真时选取的发射状态下加速度所得出的应是理论最小应力。其中最大应力出现在悬臂梁的固定端，为1.92 MPa。该数值接近于PDMS材料的拉伸强度，所以应考虑正常发射中，出现更大的应力机构作用情况：由于柔性材料的物理属性，悬臂梁可能会在固定端发生断裂，在后坐力的作用下掉入安全系统于底板的狭缝中。此时隔爆滑块不再有悬臂梁结构阻挡，依然可以稳定解除保险。

图8 位移最大时后坐保险机构的应力云图

简化模型分析证明，该悬臂梁式后坐保险机构满足理论分析得出的固有角频率范围，可以区分正常发射工作状态和意外跌落状态。意外跌落时，悬臂梁可以有效阻挡隔爆滑块的移动，起到定位作用；正常发射时悬臂梁变形不再阻挡隔爆滑块的移动，从而保证发射时安全系统的可靠解保。

4 工艺设计

目前，MEMS制造工艺主要有光刻、剥离、腐蚀、刻蚀、氧化、掺杂、气相沉淀和真空镀膜等。2004年，美国海军水面作战中心采用深硅刻蚀工艺对SOI(Silicon on Insulator绝缘体上硅)晶元进行加工，所制备的传感器芯片经键合后，其峰值形态达到了与普通集成电路相同的水平。该中心于2009年展示了另一种可抗50 000冲击的MEMS碰撞测试开关，推动了MEMS设计及工艺技术的不断进步。

本文所设计的柔性安全系统结构为Φ14 mm×0.8 mm的微型电子器件，结构相对简单，但工艺精度要求高，适合采用纳米加工技术。由于设计目的要求该MEMS器件应满足批量生产的需求，而传统的刻蚀技术和纳米结构制备效率无法达到生产需求，所以采用纳米压印技术进行该MEMS器件的制备。

纳米压印技术的核心是对图形的转移，其原理主要为：利用传统的光刻技术，以硅片为基底，构筑所需的纳米结构图案；之后基板上的模板被压入可流动聚合物中，再利用反应离子刻蚀(Reactive Ion Etching,RIE)技术去除图形区域内残留的聚合物；最后采用金属镀膜技术，在基底和聚合物上沉积金属膜，溶去聚合物，纳米结构图案就被转移到了基底上，见图9。

图9 纳米压印过程示意图

根据设计需求，本MEMS器件结构简单，所采用的材料PDMS与硅片之间具有良好的黏附性，所以应采用热压印工艺进行制作。根据前文设计所体现的该柔性MEMS安全系统的结构特征，选取了纳米压印工艺中的热压印技术对该MEMS器件进行加工。根据传统的纳米压印工艺和以柔性材料为模板的压印工艺流程设计了加工柔性MEMS的具体方法。

5 结论

1) 本文所设计的柔性MEMS安全系统，扩大了水平基板式MEMS系统引信后坐保险机构轴向行程，将传统的惯性销式保险机构优化为悬臂梁式，提高了可靠性。

2) 利用SolidWorks和COMSOL等软件建立的柔性MEMS安全系统三维模型，通过仿真分析和力学响应计算，验证了该模型的合理性。

3) 采用了纳米热压印技术，利用PDMS优良的表面黏附特性，设计出简洁、合理的加工流程，可应用于后续小口径弹药引信验证。