鄂尔多斯西南缘及邻区三维速度结构全波形反演

李俊毅， 侯卫生,2*， 郭飚， 沈旭章,2， 郑文俊,2,

1 中山大学地球科学与工程学院， 广东省地球动力作用与地质灾害重点实验室， 广州 510275 2 南方海洋科学与工程广东省实验室(珠海)， 广东珠海 519082 3 中国地震局地质研究所地震动力学国家重点实验室, 北京 100029

0 引言

鄂尔多斯西南缘位于我国青藏地块、鄂尔多斯地块、秦岭造山带几个不同构造体系的交界位置.受青藏高原和华南地块的共同作用，鄂尔多斯西南缘发育了一系列的活动断裂(邓起东等, 1999; 黄柳婷等, 2020)，使得该地区的新生代构造与早期构造相叠加，构造环境极其复杂.研究该区域深部速度结构，对于了解其复杂的构造格局以及物质运移等热点科学问题均有着十分重要的研究价值.

地震成像是获得地球深部结构的最直接、有效的方法之一.近年来，地球物理学家们在鄂尔多斯地块及其邻区开展了一系列的成像研究工作，现已取得了众多重要研究成果.主动源地震勘探剖面揭示了鄂尔多斯上地壳具有轻微的横向各向异性，莫霍面深度从西部逐渐向东部变浅(张先康等, 2003; Jia et al., 2014).地震体波层析成像研究表明了鄂尔多斯西缘上地幔速度结构存在明显的横向不均一性(郭飚等, 2004; Cheng et al., 2014; 高翔等, 2018 )；大地电磁成像研究发现鄂尔多斯内部中下地壳及上地幔存在低阻体(Dong et al., 2014; 韩松等, 2016; 李晨晶等, 2017)；背景噪声反演的研究也取得了这一区域较为一致的相速度分布特征(陈强森等, 2013; 冯红武等, 2019; 付媛媛和肖卓, 2020)；剪切波分裂研究表明：鄂尔多斯西缘的快波方向主要表现为NW-SE方向，存在岩石圈的垂直连续变形(Wang et al., 2016; 常利军等, 2016).接收函数研究对于认识该区域构造细节提供了更详细的约束(Tang et al., 2015; 黄柳婷等, 2020).为了获得更详细的深部结构，前人采用了多种成像方法结合的方法进行研究.Bao等(2015)综合背景噪声和地震面波数据得到了研究区较高分辨率vs模型.陈洁等(2020)采用接收函数方法，进行Kirchhoff偏移成像，结合该区域内已有的地震面波频散进行联合反演，获得了沿107.6°E南北向剖面鄂尔多斯地块的地壳内部精细结构.此外，GPS观测的水平速度场表明青藏高原向东扩张的运动存在明显的顺时针旋转，研究区运动方向呈现出由北东向至东向渐变的趋势(Zhang et al., 2004; Gan et al., 2007; Wang and Shen, 2020)，震源机制解反演的地壳应力场结果也有着类似的结果(Xu et al., 2016; Han et al., 2019).GPS水平速度场的速度方向与地壳应力场的最大应力方向基本一致，表明高原地壳物质存在持续向东的扩张趋势，而这种持续性的扩张势必对鄂尔多斯地块及相邻区域产生影响.为了明确青藏高原东北缘持续扩张对相邻地块相互作用的构造运动模式，Guo等(2016)通过深地震反射剖面结合多种数据，详细分析了青藏高原与鄂尔多斯地块之间构造过渡带的演化过程.Tian等(2021)利用接收函数方法论述了陇西盆地与六盘山上下地壳受青藏高原与鄂尔多斯板块相互作用导致的地壳变形模式，认为地壳内部存在解耦，但是地壳解藕发生的位置仍存在争议.因此，对于鄂尔多斯西南缘开展三维速度结构成像研究，不仅能为前人已取得的一些深部研究结果提供有力的地震学证据，还能对该区域探讨深部速度结构和浅部构造耦合提供重要的成像制约.

虽然地震成像方法众多，但基于传统射线理论的地震成像方法难以满足当代三维速度结构成像研究所需的精度要求.全波形反演方法因能充分利用地震记录中走时、振幅和相位等信息来建立高精度的地下速度结构模型，自提出以来就备受关注.全波形反演方法的基本理论提出至今已有近40年的历史(Tarantola and Valette, 1982; Tarantola, 1984, 1986, 1988).受限于三维非均匀介质中地震波场建模的巨大计算量和存储要求，天然地震全波形反演方法的实际应用主要局限于二维，三维速度结构研究较少.此外，地震波场建模计算所需的高资源消耗及高质量地震记录，限制了全波形反演方法在利用天然地震数据研究大陆壳幔结构的应用.不过随着并行计算技术的发展以及高密度地震台阵的布设，相关学者们应用该方法完成了许多构建大陆尺度壳幔结构的全波形反演研究(Fichtner et al., 2009, 2013; Tape et al., 2010; Krischer et al., 2018; Tao et al., 2018).近年来，使得全波形反演在构建高分辨率三维速度结构的研究和应用中越来越流行(Zhang et al, 2021).

本研究收集并整理了研究区内所布设的流动地震台站数据，利用全波形反演方法重构了鄂尔多斯西南缘及邻区地下的三维速度模型，结合前人资料分析并讨论了研究区的壳幔速度结构特征.

1 数据与方法

1.1 地震数据获取与处理

本文的计算域范围为29.5°N—42.5°N，100°E—111°E，吸收边界宽1.5个经纬度.计算域覆盖了青藏高原东北缘，部分阿拉善地块，鄂尔多斯西部以及部分华南地块.本研究使用的地震数据均来自于流动台站记录到的地震数据.为了保证记录数据具有足够的信噪比，从中提取了2013年12月至2016年1月发生在鄂尔多斯西南缘及周边邻区的8个4.7级以上的地震事件，共677个流动地震台站的10098个地震记录.本研究参与计算所采用8个地震事件的震源机制解均是从IRIS(http:∥ds.iris.edu/spud/momenttensor)上获得.经过去除缺道、信噪比过低和分布在计算域边界与吸收边界之间的台站数据后，最终使用了539个地震台站的6030个高质量地震记录进行全波形反演.相应的计算域、吸收边界、流动台站以及事件分布如图1所示.

图1 台站及地震事件分布图Fig.1 The distribution of seismographic stations and seismic events

1.2 全波形反演

全波形反演方法获取高精度三维速度结构模型时，以一个良好的初始模型来模拟地震波场，可以尽量避免产生明显的波形周期跳跃的问题(Virieux and Operto, 2009; Prieux et al., 2013).本文以FWEA18模型(Tao et al., 2018)作为初始模型.该模型是用Crust1.0(Laske et al., 2013)修正莫霍面深度后的EARA2014模型(Chen et al., 2015)经全波形反演得到的三维速度结构模型.采用该模型作为本研究的初始模型，不仅可以作为模型先验信息对模型进行约束，保证收敛方向的稳定性，还可以减少构建区域尺度的长周期三维初始模型的计算资源消耗.

任何反演都离不开正演，全波形反演也不例外.本研究的正演模拟和伴随模拟采用了SES3D(Gokhberg and Fichtner, 2016)计算模块.SES3D是利用谱元法模拟球面上的弹性波传播和波形反演的程序包.本研究在进行谱元模拟时，将每个单元内的位移场由4个点的拉格朗日多项式进行网格插值，即每个单元包含(4+1)3=125个网格点.模拟网格的单元总数为1485万，自由表面上的水平网格单元间距约为3.8 km，纵向网格单元间距约为4.2 km，滤波的最小周期为10 s.以上所有运算均通过天河二号超级计算机进行计算，本研究使用了384个核参与并行计算，对于每个地震事件的正演模拟时间大约40 min，而对于每个地震事件的伴随模拟时间需要1 h左右.

在通过波场模拟获得合成波形之后，确立合成波形与实际观测地震记录的走时、振幅等信息差异的目标函数是全波形反演的关键.本研究采用了滑动窗口通过傅里叶变换将数据从时间域转换到时频域，利用频率域数据随时间变化的特征，得到包含波形相位信息的时频目标函数(Fichtner et al., 2008, 2009)，其总相位失配Xp表示为

(1)

其中，Xp是时频域内所有相位差的积分，W是关于滑动窗口所选波形的加权函数，φsyn和φobs分别表示合成地震记录和观测地震记录的相位.

相比基于单个互相关走时差的目标函数，以式(1)作为目标函数的优势在于提取频率和相位信息时，不需要识别和分离各个地震震相，可直接对满足预设条件的体波、面波等所有类型的地震波进行窗口选择拾取.这不仅减缓了全波形反演的非线性，同时还增加了相位信息(Fichtner et al., 2009; 蒋梦凡等, 2021)，能最大限度地重构地下三维速度结构.

然而，该目标函数在高频窗口选择拾取时，会存在波形周跳的现象(Krischer et al., 2018).所以，在短周期的窗口拾取时需要谨慎处理.本研究采用了LASIF(Krischer et al., 2015)为全波形反演开发的窗口拾取程序，通过合成波形最短到时和最长到时以及计算周期确定选窗范围后，利用时窗滑动对窗口进行拾取，再根据归一化互相关系数、走时偏移量、包络拟合情况以及振幅能量等预设条件，对合成波形与实际波形相差太大以及未达到预设条件的时窗进行消除，以得到满足所有预设条件的波形窗口.

在迭代优化过程中，本研究采用了带有高斯先验的最速下降法来实现模型的迭代更新.由于目标失配函数求解得到的原始梯度通常包含高频奇点和小尺度数值振荡(Krischer et al., 2018)，因此引入了平滑算子用于消除那些不需要的模型梯度特征.同时，为了解决最速下降法收敛速度缓慢的问题，本研究增加了线性搜索，即每次迭代对不同步长进行搜索，通过不同步长的模型波形拟合情况来选择最优步长.模型参数更新公式如下：

(2)

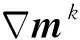
2 模型评估

2.1 模型迭代情况

在进行模型迭代优化时，为了避免陷入局部最小值，通常采用多尺度反演策略.即利用相对较长周期的地震数据拟合波形，当合成波形能够在预设条件内准确预测相位后，逐渐增加较短周期的地震信息，以此来获得模型高频结构(Bunks et al., 1995; Fichtner et al., 2013; Krischer et al., 2018).本研究分别在两个不同频段上完成了模型的迭代优化.模型迭代情况如图2所示，蓝线代表20～40 s长周期的模型迭代情况；绿线代表10～40 s短周期的模型迭代情况；橙红色五边形代表搜索步长不是当前迭代最优步长或搜索方向有误而弃用的实验模型.相对波形总失配比是后续模型得到的波形失配总量相对于每个频段初始模型时的波形失配总量的比值.

图2 模型迭代与相对波形失配比关系图Fig.2 The relationship between model iteration and relative waveform misfitting ratio

经20次的迭代更新，获得了最终的速度模型.随着模型更新次数的增加，新模型的相对波形总失配比一直保持持续下降的趋势，证明每次更新得到的新模型波形拟合能力在逐渐增强.对于20～40 s的长周期频段，本研究进行了9次模型更新，弃用了5个实验模型.前6次的模型更新，相对波形总失配比下降速度较快.从第6次模型更新后，整体失配效果并不随迭代次数的增加而显著改善.因此，在继续更新了三次后，本研究选用第9次模型更新所获得的模型作为10～40 s短周期数据反演的初始模型继续进行反演.对于10～40 s短周期频段，本研究进行了11次模型更新，弃用了7个实验模型.由于短周期数据存在大量高频信息，为了保证模型的有效更新，在更新5次后，本研究缩小了模型更新步长，来保证模型更新的稳定性.第15次更新后，模型的相对波形总失配比仍在下降，但是模型更新开始不会显著提高模型的波形拟合效果.此外， 20次更新后的模型仍可以减小波形总失配比，但是在震源周围产生了明显的局部数值震荡.因此，我们在第20次迭代之后终止了模型更新.

2.2 波形拟合情况

为了验证最终模型的波形拟合能力，我们将初始模型正演模拟得到的合成波形与最终模型正演模拟得到的合成波形进行对比(图3).图3a为不同震中距的部分台站与相对应地震事件的射线路径，图3b为相对应台站波形拟合情况.其中，蓝线为初始模型正演模拟得到的合成波形，红线为最终模型正演模拟得到的合成波形，黑线为台站实际记录到的地震波形.为了更好地分析波形相对应的台站，图3a中每个台站与地震事件间射线路径的颜色与图3b中台站的颜色一致.

图3 部分台站波形拟合图(a) 不同震中距部分台站与相对应地震事件的射线路径； (b) 相对应的台站波形拟合情况.Fig.3 Waveform fitting on some stations(a) Ray paths of some stations with different epicentral distances and corresponding seismic events (b); (b) Waveform fitting on corresponding station.

从图3来看，相较于初始模型正演模拟得到的合成波形，最终模型正演模拟得到的合成波形的相位和振幅以及波形互相关系数均得到了一定的改善，说明最终模型得到的合成波形更接近台站实际观测到的真实波形.对于部分台站的波形，如CA.15601，CA.61027，CA.61067，CA.62412，CA.64036，最终模型正演模拟得到的合成波形几乎与实际波形一致.然而，模型更新后，台站CA.51507波形基本上没有变化，说明最终模型可以保留初始模型中波形拟合好的模型细节.图4给出了模拟期间不同频段上，CA.61062和CA.15709两个台站的三分量波形拟合情况，两个台站与对应地震事件的分布见图3.相较于初始模型正演模拟得到的合成波形，最终模型所得到的地震波形在两个频段上的相位和振幅均得到了明显改善.除了面波之后到达的长周期尾波外，最终模型的合成波形都可以在相位和振幅上与实际记录相匹配.此外，本研究所采用方法对面波拟合能力较好，其主要原因是面波能量强，可保证模型更新过程中的低频约束.而对于多次波以及一些未知震相，尽管本研究选用的时频目标函数不会受数据振幅的影响，但由于这些震相体现的是模型中不易稳定的高频结构，所以仍会存在一些波形拟合不足的情况.

图4 不同频段三分量波形拟合情况(a) CA.61062台站20～40 s的三分量波形拟合情况; (b) CA.61062台站10～40 s的三分量波形拟合情况; (c) CA.15709台站20～40 s的三分量波形拟合情况; (d) CA.15709台站10～40 s的三分量波形拟合情况.Fig.4 Waveform fitting of three components in different frequencies(a) Three component waveform fitting of CA.61062 station in 20～40 s; (b) Three component waveform fitting of CA.61062 station in 10～40 s; (c) Three component waveform fitting of CA.15709 station in 20～40 s; (d) Three component waveform fitting of CA.15709 station in 10～40 s.

为了定量分析最终模型相较于初始模型在不同频段下波形拟合情况，本研究分别统计了初始模型和最终模型在每个流动台站的波形归一化互相关系数(图5).黑线代表初始模型波形互相关系数统计结果，红线代表最终模型波形互相关系数统计结果.图5表明无论是在20～40 s的长周期频段(图5a)，还是在10～40 s的短周期频段(图5b)，最终模型的波形互相关系数都比初始模型的波形互相关系数高.这说明最终模型得到的合成波形更加贴合台站记录到的实际波形.20～40 s长周期频段的互相关系数峰值在0.8(图5a)，而10～40 s短周期频段互相关系数无明显峰值，主要分布在0.1～0.8之间(图5b).这说明20～40 s长周期频段的波形拟合结果明显优于10～40 s短周期频段的波形拟合结果.其原因为短周期数据中携带大量高频的地质结构信息，而这些高频的波形数据较难拟合，导致最终模型的短周期互相关系数较长周期互相关系数低.

图5 波形互相关系数直方图Fig.5 Histograms of cross correlation of waveform

3 模型结果分析及讨论

本研究依托全波形反演方法，获得了鄂尔多斯西南缘及邻区的三维速度结构.经过20次模型更新，最终模型相较于初始模型的波形拟合能力得到了一定的提升.为了明确最终模型速度结构反映的地质意义，还需结合相关研究对鄂尔多斯地块西南缘及邻区的速度结构特征进一步讨论分析.本研究以AB、CD、EF、GH、IJ等5个垂向剖面分析最终模型的速度结构特征(垂向剖面位置见图1).此外，为了对比本研究对于初始模型的变化，我们也在这5个垂向剖面位置将初始模型与最终模型P波和S波速度结构进行对比.图6和图7分别为初始模型的P波和S波速度垂向剖面，图8和图9分别为最终模型的P波和S波速度垂向剖面，图10和图11分别为最终模型相对初始模型的P波和S波相对速度垂向剖面.每个垂向剖面图的灰色填充区代表地表高程，黑色虚线代表地块分界线.

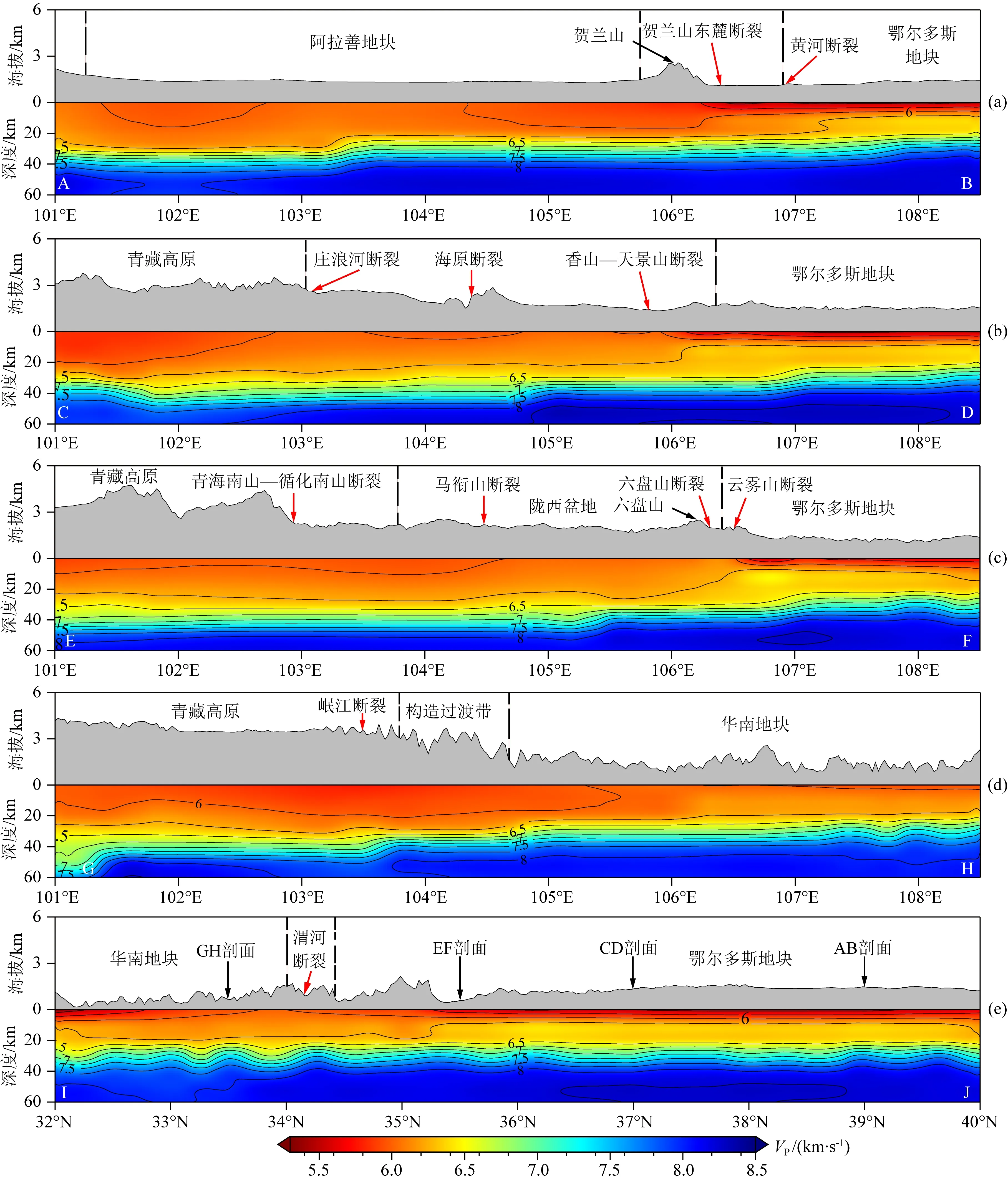
图6 初始模型P波速度垂向剖面(a)—(e)分别表示AB、CD、EF、GH、IJ的垂向剖面.图中数字代表地震波速，单位为km·s-1.Fig.6 Vertical sections of P-wave velocityfrom initial model(a)—(e) Denote the vertical profiles of AB, CD, EF, GH and IJ respectively. The number in the figure represents the seismic wave velocity.The unit is km·s-1.

图7 初始模型S波速度垂向剖面(其他说明同图6)Fig.7 Vertical sections of S-wave velocityfrom initial model (Others are the same as Fig.6)

图8 最终模型P波速度垂向剖面(其他说明同图6)Fig.8 Vertical sections of P-wave velocityfrom final model (Others are the same as Fig.6)

图9 最终模型S波速度垂向剖面(其他说明同图6)Fig.9 Vertical sections of S-wave velocityfrom final model (Others are the same as Fig.6)

图11 S波相对速度垂向剖面(其他说明同图6)Fig.11 Vertical sections of S-wave relative velocity (Others are the same as Fig.6)

3.1 速度结构分析及讨论

从P波的模型对比情况来看(图6与图8)，最终模型和初始模型的速度结构没有显著差异，仅在贺兰山附近以及各地块交界的构造过渡带部分区域速度结构发生了一些改变.相较于初始模型，S波速度结构最终模型的变化十分明显，尤其是对于地壳部分的改变更为显著(图7和图9).这反映了P波对于地下介质各向异性的敏感程度不如S波.因此，最终的模型分析主要是围绕S波速度结构特征来展开.需要注意的是，鄂尔多斯地块和华南地块的沉积层P波和S波速度结构基本没有发生变化.此外，对于剖面中存在的断裂，在初始模型中均未发现速度异常(图6和图7)，但经模型更新后，断裂附近对应的速度结构均出现明显的速度异常(图8和图9).

AB剖面是沿北纬39°跨越阿拉善地块、贺兰山和鄂尔多斯地块的垂直剖面(图9a).AB剖面显示相较于阿拉善地块，鄂尔多斯地块地壳速度结构沉积层呈明显低速，沉积层下速度结构迅速转换为明显高速，表现出古老克拉通稳定的岩石结构特征.而阿拉善地块内部壳幔速度结构相较于鄂尔多斯地块复杂，主要是由于阿拉善地块具有复杂的地质演化历史(Zhao et al., 2001; Yuan and Yang, 2015)，形成了复杂的速度结构特征.CD剖面为沿北纬37°跨越青藏高原和鄂尔多斯地块的垂直剖面(图9b).在该剖面中，鄂尔多斯地块内部沉积层呈明显低速，沉积层的高速结构中又存在不连续分布的低速体，上地幔速度结构连续.这表明沉积层下方原本呈稳定克拉通的岩石结构发生了一定改变.EF剖面是沿北纬35.5°跨越青藏高原、陇西盆地、六盘山和鄂尔多斯地块的垂直剖面(图9c).该剖面中鄂尔多斯地块内部速度结构与CD剖面具有相似特征.在陇西盆地下方20 km处存在明显的低速体，接收函数结果表明该低速体有可能为陇西盆地上地壳沿六盘山断裂逆冲到鄂尔多斯地块上形成的残余上地壳物质(Tian et al., 2021).此外，六盘山和鄂尔多斯地块交界处的云雾山断裂东西两侧速度结构存在明显差异，反映了明显的构造分界特征.GH剖面是沿北纬33.5°跨越青藏高原和华南地块北部的垂直剖面(图9d).GH剖面显示华南地块北部地壳速度结构不存在明显低速沉积层和高速层，上地幔速度结构连续.有成像结果表明华南地块与鄂尔多斯地块一样均为稳定的古老克拉通(Tao et al., 2018)，但本研究结果表明华南地块北部并没有呈现出古老克拉通的速度结构特征.

IJ剖面是沿东经108°跨越鄂尔多斯地块和华南地块(图9e).该剖面显示鄂尔多斯地块地壳速度结构低速沉积层明显，地块内部下地壳中存在不连续分布的低速体，上地幔速度结构连续.华南地块内部(33°N以南)壳幔速度结构与鄂尔多斯地块相似，低速沉积层明显，沉积层下速度结构迅速转换为高速，呈现出古老克拉通的结构特征.在鄂尔多斯地块内部北纬38°处附近，壳幔结构都存在明显速度差异，北部地壳部分呈高速，上地幔呈低速，南部地壳呈低速，上地幔呈高速.这一结果与前人接收函数、大地电磁、层析成像和联合反演的研究结果相吻合(Tian et al., 2011; Dong et al., 2014; 高翔等, 2018; 陈洁等, 2020).值得注意的是，Tang等(2015)利用接收函数发现在北纬35°附近，鄂尔多斯地块下方20 km处存在一宽0.5°的低速体，并认为该低速体的存在可能表明稳定的鄂尔多斯克拉通的岩石结构受青藏高原的挤压作用而产生了改变.本研究的最终模型在鄂尔多斯地块下方20 km处也观测到相似的低速体，进一步佐证了鄂尔多斯地块中下地壳的改变.

此外，图9中断裂下方的速度结构均出现明显异常，由于受模型精度所限，本研究结果虽然无法清晰地反映出其断裂形态，但是断裂的延伸方向与断裂下方速度异常的分布方向大致相同.其中黄河断裂、庄浪河断裂和云雾山断裂附近，东西两侧速度结构存在明显差异，清晰地揭示了地块与构造过渡带间构造分界.

3.2 相对初始模型速度结构分析及讨论

为了直观对比最终模型和初始模型速度结构的模型更新情况，图10和图11展示了最终模型相对于初始模型的P波和S波的相对速度结构.P波和S波相对速度结构对于研究区内大部分构造单元的速度结构变化情况相同，但对于局部构造过渡带的速度变化略有不同(图10d与图11d).P波速度与S波速度在地壳部分相较于上地幔处改变明显，地壳部分速度更新量较大，上地幔速度更新量较小.此外，山脉、断裂、构造过渡带以及地块内部下方模型的更新量较大，而地块边缘的模型更新量较小.贺兰山、六盘山、陇西盆地、鄂尔多斯地块以及华南地块内部下方的P波和S波相对速度均明显降低.而阿拉善地块西部以及部分地块过渡带相较于初始模型，P波相对速度明显增加，S波相对速度明显降低，这反映了对初始速度模型的更新变化.在断裂附近，P波相对速度变化并不明显，相对速度均存在少量降低(图10).但是，除渭河断裂附近相对速度少量变化外，其余断裂附近S波相对速度明显降低(图11).这说明在反演过程中，S波速度结构受断裂影响明显.

4 结论

本文采用基于伴随谱元的全波形反演方法，经过20次模型更新，获得了鄂尔多斯西南缘及邻区的P波和S波三维速度结构，结合前人研究成果对研究区内速度结构特征进行分析，揭示了鄂尔多斯地块西南缘与相邻地块以及构造过渡带的地壳和上地幔顶部的速度结构特征，得到以下结论.

(1)本研究获得的三维速度结构模型相较于研究区现有的模型波形拟合效果更好.除了一小部分波形细节外，最终模型正演模拟的合成波形基本都可以在相位和振幅上与实际记录到的波形相匹配.

(2)鄂尔多斯地块以及邻区的地壳和上地幔顶部存在地震波速明显的横向变化.从分布的位置来看，这种不均匀性主要分布于不同地块之间的构造过渡带，且在地块内部也存在少量分布.

(3)鄂尔多斯地块地壳沉积层呈明显低速，地块轮廓清晰可见；在沉积层之下，鄂尔多斯地块和华南地块内部呈现明显高速，表现出古老克拉通稳定的岩石结构，但华南地块北部地壳并未体现相似的速度结构特征.相较于鄂尔多斯地块和华南地块，阿拉善地块内部壳幔速度结构复杂，反映了其具有更复杂地质结构.

(4)在北纬38°以北，鄂尔多斯地块内部部分地壳速度结构呈高速，上地幔呈低速，而地块南部地壳速度结构则具有相反的特征.此外，鄂尔多斯地块内部存在的不连续低速体，进一步表明鄂尔多斯古老稳定克拉通的岩石结构已经发生了改变.

(5)断裂附近的速度异常说明断裂对速度结构具有显著影响.其中，黄河断裂、庄浪河断裂和云雾山断裂附近，东西两侧速度结构差异明显，反映了明显的构造分界特征.

致谢文中图件均使用GMT(Wessel et al., 2013)进行绘制，感谢ETH的Lion Krischer博士对于编写相关代码的指导和帮助，感谢广州天河超算中心提供的计算平台，感谢两位审稿专家提出的建设性意见.