电子互连导电胶的力学性能及胶连点跌落冲击行为

熊 蘅，马宇宏，司博文，肖革胜，树学峰

（太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024）

电子产品的无铅化使得电子互连材料由传统的锡铅焊料逐渐向无铅焊料和导电胶转变[1-3]。导电胶具有工艺温度低、加工成本低及导电性优良等优点[4-5]，在半导体表面封装、印刷电路板及压电陶瓷等领域具有广泛的应用前景。由于电子产品在其生产运输和日常使用过程中易受到跌落冲击载荷作用[6]，而跌落过程中封装芯片与基板之间的细小互连点是最容易失效破坏的关键部位，因此有必要开展导电胶互连点的跌落冲击力学响应研究。

目前，已有诸多学者通过改变胶体基体、固化剂、导电填料的类型等对导电胶的性能进行了多方面的优化[7-10]。Zhan 等[8]基于自烧结银微粉框架研究了其在低温固化导电胶中的应用，结果表明，应用表面改性银粉作为导电填料在较低温度下具有良好的导电性与黏合强度；Springer 等[10]通过动态机械热分析仪对5 种不同导电胶进行了黏弹性材料的表征测试，获得了相关材料参数，并采用广义麦克斯韦模型描述了导电胶的黏弹性行为。此外，对于电子封装结构跌落冲击时互连点的研究多集中于无铅焊点[11-14]。杨雪霞等[11]分析了3 种不同形状无铅互连焊点对球栅阵列封装板级封装跌落冲击载荷下可靠性的影响，结果表明，沙漏形焊点具有相对较好的抗跌落冲击性能；He 等[13]建立了基于位错密度的无铅焊点在跌落冲击下的黏塑性本构模型，并对焊点的黏塑性变形进行了数值模拟；Long 等[14]采用分离式霍普金森压杆研究了SAC305 无铅焊料在高应变率下的动态行为，用应变率相关的Johnson-Cook 模型对其动态行为进行了描述。目前关于较高应变率下导电胶动态力学行为的测试表征以及封装结构跌落冲击下胶连点动态力学响应的研究较少。

本研究将对不同应变率下电子封装中典型各向同性导电胶（isotropic conductive adhesive，ICA）的力学性能进行测试，从而获得其应变率相关的本构关系。鉴于实际封装结构及其使用工况的复杂性，进一步通过数值模拟研究导电胶互连封装结构的跌落冲击力学行为，对导电胶互连点在同一高度不同角度、不同高度同一角度跌落冲击下的可靠性进行分析，研究结果对于胶连电子器件封装结构的优化设计及提高其跌落工况下的服役可靠性具有重要意义。

1 实 验

1.1 实验材料及试样制备

本实验所用材料为上海安巅新材料科技有限公司加工的AS-6509B 导电银胶（银含量为60%）。该导电银胶为环氧树脂基、120 ℃中温固化ICA，产品无溶剂，可以很大程度上减少在固化过程中产生的孔洞数量，主要成分有导电银粉、环氧树脂、树脂固化剂（酸酐类）、偶联剂等。

试样制备前，将导电银胶从低温恒温试验箱内取出，静置于室温中解冻0.5 h。同时，预热高温恒温试验箱，以减缓实验时环氧树脂与固化剂之间的反应。使用 ∅4.5 mm 的医用注射器将导电胶注入∅5 mm 的耐高温塑料软管中，静置2～3 min 后将其放入高温恒温试验箱中；试样在120 ℃恒温试验箱中固化2 h 后自然冷却；将固化后的导电银胶试样从试管中取出，进行打磨抛光处理，得到尺寸为 ∅5 mm ×5 mm 的圆柱体试样。图1 为固化后的导电胶试样和扫描式电子显微镜（scanning electron microscope，SEM）下的微观表面形貌。

图1 各向同性固化导电胶试样(a)及其SEM 图像(b)Fig. 1 Test sample (a) and SEM image (b) of cured ICA

1.2 固化导电胶的静动态力学性能实验

采用万能试验机（ETM105D）对固化导电胶试样进行两种不同应变率（0.01 s−1和0.10 s−1）下的准静态测试，每种应变率下进行3 组重复实验，选取其中1 组代表性结果用于后续研究，得到 ICA 的准静态真应力-应变曲线，如图2(a)所示。

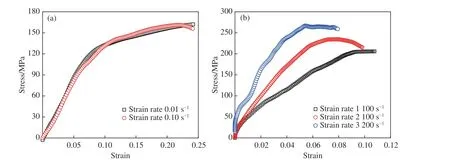
图2 各向同性固化导电胶的准静态(a)和动态(b)真应力-应变曲线Fig. 2 Quasi-static (a) and dynamic (b) true stress-strain curves of cured ICA

采用分离式霍普金森压杆装置[15]对固化导电胶进行动态压缩测试，应变率控制在1 000～3 500 s−1范围内。实验在室温下进行，每组应变率下进行3 次重复实验，选取其中一组代表性结果用于后续研究，得到了3 种动态应变率下的真应力-应变曲线，如图2(b)所示。应用文献[16]中的方法确定相应的动态屈服强度，具体结果见表1。

表1 不同应变率下固化导电胶的动态屈服强度Table 1 Dynamic yield strength of cured ICA at different strain rates

2 跌落冲击数值模拟

2.1 有限元模型和材料属性

参照JESD22-B111 标准[17]，建立了导电胶互连封装结构自由跌落模型。只考虑在印制电路板（printed-circuit board，PCB）中心位置安装一块封装件，然后通过4 个M3 螺柱固定在刚性基座上[18]，如图3(a)所示。PCB 板距离基座10 mm，基座下面是撞击平台。封装结构模型从上到下分别为PCB 板、铜盘、导电胶胶连点、铜垫、基板、芯片和封装树脂，如图3(b)、图3(c)所示。PCB 板为132 mm×77 mm×1 mm 的均质板，共有49 个胶连点，相邻胶连点间距为1.27 mm，胶连点为直径0.56 mm、高度0.58 mm的圆柱体；芯片为5.08 mm×5.08 mm×0.25 mm 的正方形薄片，基板为10 mm×10 mm×0.26 mm 的均质薄板；基板一侧与PCB 板一侧的铜盘均为直径0.56 mm、高度0.02 mm 的薄片，环氧树脂厚度为0.54 mm。

图3 导电胶互连封装结构自由跌落模型Fig. 3 Free drop model of ICA packaging structure

基板、PCB 板属性为横观各向同性[19]，相关参数见表2。其中：Ex、Ey、Ez分别为x、y、z方向的弹性模量；Gxz、Gyz、Gxy和γxz、γyz、γxy分别为xz、yz、xy面内的剪切模量和泊松比。螺柱、芯片、铜盘、环氧树脂均视为线弹性材料，基座与撞击平台均视为刚体，具体参数见表3[18-19]。其中：E、γ、 ρ分别为材料的弹性模量、泊松比和密度。导电胶的相关材料力学参数见表4，其中，C和P为材料常数。

表2 基板和PCB 板的横观各向同性参数Table 2 Transversely isotropic parameters of substrate and PCB board

表3 各材料的力学参数Table 3 Mechanical parameters of materials

表4 ICA 的力学参数Table 4 Mechanical parameters of cured ICA

2.2 载荷条件和跌落工况

在自由跌落碰撞过程中，忽略空气阻力和摩擦力的影响，只对模型施加重力，对撞击平台完全固定约束。为了节省计算时间，刚性基座与撞击平台直接接触，但给模型施加相应的初始速度（4.43 m/s），相当于从1.0 m 高的地方无初始速度自由跌落。分析步长设置为10 ms。

首先，模拟导电胶互连封装结构随基座在同一高度（重心下降1.0 m）、0°～30°范围内6 个不同角度跌落工况下胶连点的力学响应；然后，选取同一跌落角度（5°），研究5 种不同高度跌落工况下胶连点的力学响应。除水平跌落外，其他角度均定义为小角度跌落，且同一小角度跌落均有两种不同跌落方式，一种为基座短边跌落，另一种为基座长边跌落。跌落角度为15°时两种不同跌落方式如图4 所示。

图4 同一角度两种跌落方式示意图Fig. 4 Schematic diagrams of two drop modes at the same angle

3 实验和数值模拟结果

3.1 固化导电胶的应变率效应及本构关系

由图2(a) 可知，选取的ICA 在准静态低应变率下无明显的率效应，说明其在准静态时具有一定的韧性，同时可得到固化导电胶的弹性模量和静态屈服强度分别为1 630 和130 MPa。由图2(b) 可知，在动态较高应变率下ICA 的率效应明显，整体呈现脆性破坏状态，说明在较高应变率下表现出了明显的韧脆转变，且应变率越高，破坏时的应变越小。这是因为固化导电胶基体是黏性的环氧树脂基体，高应变率加载下其黏性变形不能充分释放，导致破坏时产生了更高的载荷和相应更低的应变。

为了描述冲击载荷作用下导电胶胶连点的力学行为，采用理想塑性模型，选取只考虑应变率效应的Cowper-Symonds 本构进行理论表征

通过式(2)和实验数据对固化导电胶进行本构参数拟合，如图5 所示。通过拟合得到的直线方程求得C和P的具体值。固化导电胶密度为4 050 kg/m3，泊松比设为0.4[20]，导电胶的相关力学参数见表4。

图5 各向同性固化导电胶的本构参数拟合结果Fig. 5 Constitutive parameters fitting curve of cured ICA

3.2 关键胶连点位置及 z向最大应力

关键胶连点是封装结构所有胶连点中受力变形最大的位置，胶连点受力主要由PCB 板上、下弯曲引起，所以有必要研究PCB 板的弯曲变形。图6(a)为基座从1.2 m 高度水平跌落后胶连点产生最大z向应力时PCB 板的位移云图，图6(b)为基座长边5°跌落后胶连点产生最大z向应力时的位移云图。图6 中，S为位移，Sz表示z方向的位移。水平跌落时，由于结构具有对称性，PCB 板的弯曲变形呈板中心对称，关键胶连点位于封装件的4 个边角处；而小角度跌落时，PCB 板的弯曲变形则无法呈板中心对称，关键胶连点会出现在某一单侧的边角处。因此，本研究中的所有跌落工况，关键胶连点均位于4 个边角处的胶连点上。

图6 PCB 板的z 向位移云图Fig. 6 z-axis displacement contour of PCB board

不同跌落工况下关键胶连点的z向最大应力见表5，其中： σ0、 σ1和 σ2分别为水平跌落、基座短边5°跌落和基座长边5°跌落时的z向最大应力， σ11和 σ12则为1.0 m 高度小角度跌落时基座短边跌落和基座长边跌落时的z向最大应力。研究发现， σ0均为正值， σ2和 σ12均为负值。 σ0为正值是因为水平跌落时，PCB 板受重力等因素影响向下弯曲的幅度比向上弯曲的幅度大，所以关键胶连点受拉应力更大；而 σ2和 σ12为负值则是因为基座长边跌落时，短时间内的两次碰撞会使PCB 板形成如图6(b)所示的弯曲变形，一侧向上凸起，另一侧向下凹陷，从而导致胶连点处受到更大的压应力。

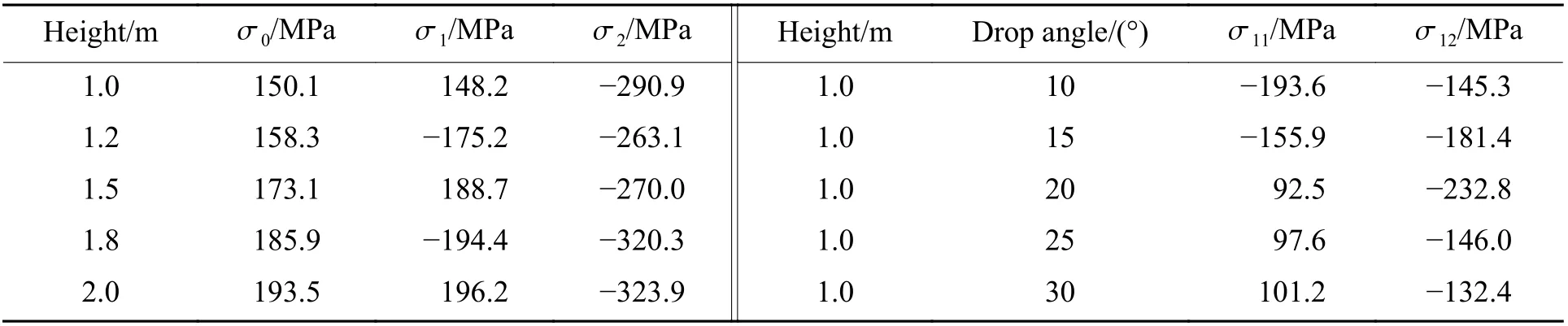
表5 不同跌落工况下的 z向最大应力Table 5 Maximum z-axis stress under different drop conditions

3.3 不同跌落角度下的应力、应变分析

图7 给出了导电胶封装结构随基座在1.0 m 高度、不同角度跌落时，关键胶连点的最大等效应力和最大等效塑性应变（PEEQ）。水平跌落时，最大等效应力为128.7 MPa，导电胶未发生屈服，无相应的塑性应变；基座长边跌落角度为5°、20°时，关键胶连点处的受力变形较大，说明这两种跌落工况下PCB 板发生的变形相对其他工况更加剧烈；基座长边跌落角度为25°、30°时，其最大等效应力均小于水平跌落下的等效应力，且未发生塑性变形，因为这两个角度跌落时，碰撞后的动能大多用于结构的整体旋转，而不是使PCB 板发生弯曲变形，所以相应胶连点处的应力和应变不大。

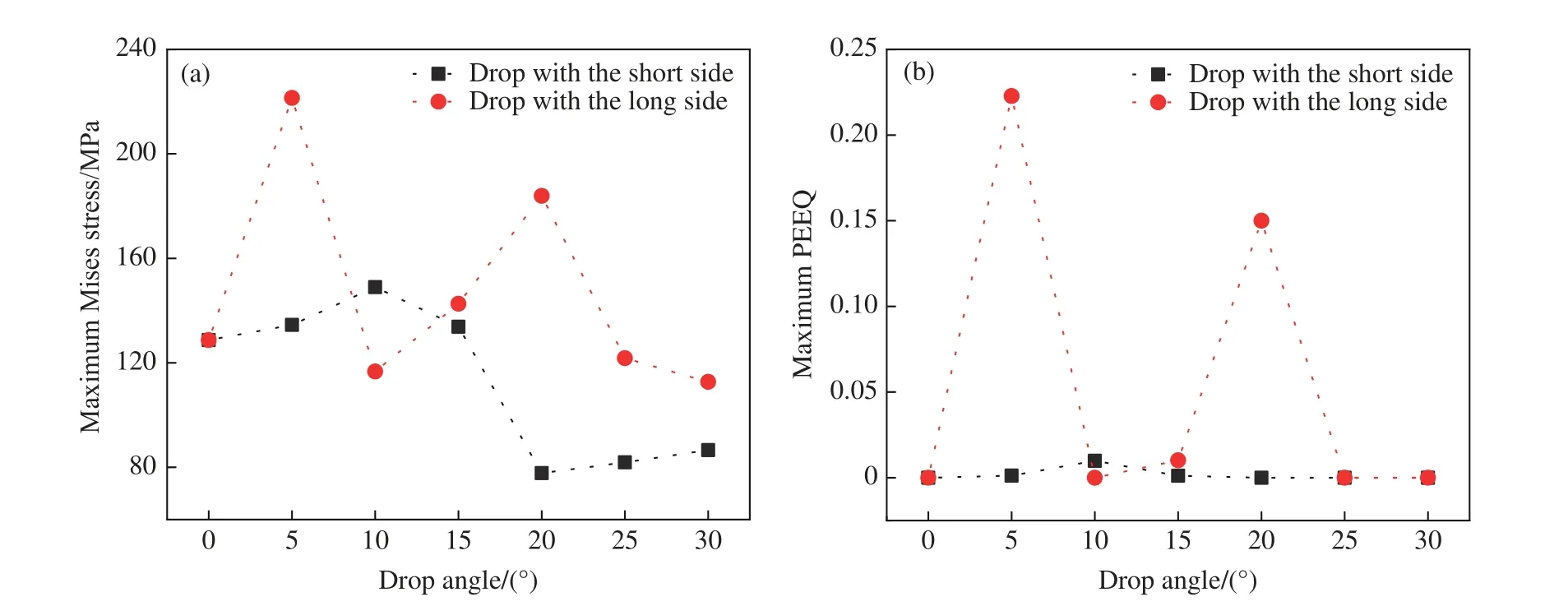
图7 不同跌落角度下的最大等效应力(a)和最大等效塑性应变(b)Fig. 7 The maximum Mises stress (a) and maximum PEEQ (b) at different drop angles

从图7 可以看出：对比水平跌落，基座短边跌落时，5°、10°和15°跌落产生的应力、应变均更高；基座长边跌落时，5°、15°和20°跌落产生的应力、应变也比水平跌落时大。这说明对导电胶互连封装结构而言，水平跌落并不是最危险的工况，小角度跌落时相对更加危险。

3.4 不同跌落高度下的应力、应变分析

为了验证小角度跌落时其他跌落高度下关键胶连点是否更容易被破坏，特选取5 种不同跌落高度，研究水平与5°跌落时关键胶连点等效应力、应变的最大值，如图8 所示。水平跌落时，随着高度的增加，应力基本呈线性上升，而应变则在后期上升相对较快；水平跌落时，撞击后PCB 板的弯曲变形模式为上下周期振动，跌落高度越大，则碰撞后PCB 板的弯曲程度更大，胶连点受力变形也就越大。基座短边跌落角度为5°时，不同跌落高度下的最大等效应力均大于水平跌落时，但在1.8 m 跌落高度下，最大PEEQ 反而比水平情况下低，这是由于水平跌落时，PCB 板周期振动过程中多次导致导电胶发生屈服，累积的应变更高。

图8 不同跌落高度下的最大等效应力(a)和最大等效塑性应变(b)Fig. 8 The maximum Mises stress (a) and maximum PEEQ (b) at different drop heights

当基座长边跌落角度为5°时，不同跌落高度下的最大等效应力和PEEQ 均大于水平跌落和基座短边跌落角度为5°时，说明这3 种跌落工况中基座长边跌落最危险。值得注意的是，基座长边跌落角度为5°时，跌落高度为1.0 m 下的最大等效应力和PEEQ 比跌落高度为1.2 、1.5 m 下更大，这是因为跌落高度为1.0 m 时的第2 次碰撞时间滞后于另外两种，使得PCB 板在第1 次和第2 次碰撞时产生应力波协同作用，进而导致关键胶连点产生了更大的应力。

4 结 论

在动态较高应变率下固化导电胶呈现脆性破坏状态，其动态屈服应力和应变具有明显的应变率效应。导电胶互连封装结构跌落冲击时，关键胶连点出现在4 个边角处，同时小角度跌落比水平跌落更容易导致胶连点发生破坏。通过分析不同跌落高度下关键胶连点的应力和应变，可以判断出小角度跌落时基座长边跌落方式更危险。