基于复合神经网络的多元水质指标预测模型

王昱文，杜震洪*，戴震，刘仁义，张丰

（1.浙江大学 浙江省资源与环境信息系统重点实验室，浙江 杭州 310028；2.浙江大学地理信息科学研究所，浙江 杭州 310027）

基于复合神经网络的多元水质指标预测模型

王昱文1，2，杜震洪1，2*，戴震1，2，刘仁义1，2，张丰1，2

（1.浙江大学 浙江省资源与环境信息系统重点实验室，浙江 杭州 310028；2.浙江大学地理信息科学研究所，浙江 杭州 310027）

长江流域在我国水资源配置体系中具有重要地位，对其进行水质预测尤为重要。基于现有研究结果，结合循环神经网络（recurrent neural network，RNN）中的门控循环单元（gate recurrent unit，GRU）模型与全连接神经网络（fully connected neural network，FCNN），提出了改进的多元水质指标预测（MWQPP）模型，并用其预测长江流域水体的pH、溶解氧（DO）、高锰酸盐指数（CODMn）、氨氮（NH3-N）。基于长江流域2011—2018年23个水质监测点7 566条原始数据，经对比实验，证明了用MWQPP模型预测得到的均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和决定系数（R2）均优于传统水质预测模型，有效提升了水质预测的精度，具有较好的鲁棒性，为水质预测和流域管理提供了科学支撑。

水质预测；人工神经网络；门控循环单元（GRU）；全连接神经网络（FCNN）

我国水系主要分为长江、黄河、松花江、珠江、海河、淮河和辽河七大流域。其中，长江流域指长江干流和支流流经的区域，长江作为我国第一大河，干流全长超过6 300 km，自西而东流经11个省（直辖市、自治区），支流展延至8个省（自治区），流域面积达1.80×106km2，覆盖全国约19%的区域。因此，长江流域在我国水资源配置中具有重要地位，其水质变化深刻影响社会经济的发展，对其进行水质预测与评估显得尤为重要。然而，目前大多研究主要集中于水质评估，针对长江流域水质预测的研究不多。

现有的水质预测方法主要有水质模拟模型、时间序列分析、回归分析、传统机器学习、人工神经网络等。水质模拟模型是早期广泛使用的一种水质研究方法，通过选取一系列水质指标，建立数学模型，预测未来水质变化，如WASP模型［1］、QUAL模型［2］、SWAT模型［3］等。这些模型可以较准确地模拟基本水质规律，但往往只适用于小范围水域，如特定的水库、湖泊、河流等，通用性欠佳。时间序列分析，运用加权平均等数学方法建立模型，其中的自回归方法常被用于中、短期水质预测，如自回归（AR）模型［4］、自回归差分滑动平均（ARIMA）模型［5］等。其优点是无须依赖外生变量；但存在以下限制：只能用自身的历史数据进行预测，且需要足够长历史序列；数据必须具有自相关性；数据必须为平稳性序列，否则要先进行差分运算，易造成信息损失；只能捕捉线性关系，对非线性关系捕捉不佳。回归分析，用回归方程拟合自变量和因变量的关系，在预测水质时，往往需先分析水质指标之间的相关系数，再据此回归预测特定指标，常用的有线性回归模型、岭回归分析、多元回归分析［6］等。对于受多种因素互相作用影响的水环境，考虑多变量的回归分析具有独特优势，当情况简单时预测效果较好，然而即使是非线性回归，每个单元也需进行线性组合，因此回归分析难以很好地表达高度复杂的数据。

传统机器学习以机器模拟人的学习机制，在学习过程中不断完善。常用的有支持向量回归［7］、随机森林、决策树等，也有将机器学习算法与各种参数优化算法相结合，如变分模态分解（VMD）［8］、遗传算法（GA）［9］等。因机器学习算法高度非线性，非常适合水质预测，能从原始特征中学习高级特征，从而更好地拟合数据波动，但模型的解释性较差。人工神经网络是实现机器学习的一种手段，其由多个神经元连接而成，通常可划分为输入层、隐藏层、输出层，随着计算机运算能力的提升，人工神经网络逐渐在各个领域得到推广。因人工神经网络具有非线性和自学习能力，在水质预测中具有独特优势，例如王晓萍等［10］利用反向传播（back propagation，BP）神经网络预测了钱塘江水质指标；宓云軿等［11］采用LM-BP神经网络和支持向量机预测了化学需氧量的变化情况；SAIFUL等［12］在红树林河口区海水水质指数预测中，发现引入ANN较多元线性回归结果更好；RAJAEE等［13］综合比较了ARIMA等水质模拟模型与SVR、ANN及多方法复合模型之间的差别，发现加入神经网络后水质预测性能得到了提升；TA等［14］将CNN运用于溶解氧的预测，获得了较传统BP神经网络更好的结果。

目前用于水质预测的人工神经网络主要有全连接神经网络（fully connected neural network，FCNN）、循环神经网络（recurrent neural network，RNN）、基于长短期记忆神经网络（long short-term memory networks，LSTM）模型改进的RNN等。例如NOORI等［15］提出的结合SWAT的FCNN模型，WANG等［16］利用CNN-LSTM复合模型预测了城市污水的化学需氧量。近年来，有学者将门控循环单元（gate recurrent unit，GRU）模型引入水质预测领域，如TU等［17］提出的CNN-GRU复合模型，但GRU模型的应用仍较少。

针对长江流域的研究现状和传统水质预测方法的不足，本研究使用多模块GRU，在长期记忆和反向传播中保留长期序列信息，避免梯度消失问题的发生，考虑指标间的互相影响，并联输入多层全连接（FC），以提高模型稳定性，最终构建了针对长江流域的多元水质指标预测（multivariate water quality parameter prediction，MWQPP）模型。同时设计了相关实验和模型评级体系，并与多元线性回归、随机森林、全连接神经网络、LSTM神经网络等模型进行了对比，证明MWQPP模型具有较高的准确性和良好的鲁棒性。

1 研究方法

1.1 全连接神经网络

BP神经网络是最传统的神经网络之一，使用的是反向传播算法。FCNN是其基础模型，可分为输入层、隐藏层、输出层，隐藏层常有多层，每一层的输出为下一层的输入，以非线性函数进行激活。

在BP神经网络训练中，用损失函数反映每次迭代（epoch）的前向计算结果与真实值之间的差距，用梯度下降法更新权重，逼近损失函数的最小值，利用BP原理求解梯度，指导下一迭代的训练不断向最优解靠拢。常用的有均方差损失函数、指数损失函数、交叉熵损失函数等。BP神经网络的训练流程如下：

Step 1 用自定义的参数初始值，进行前向传播，计算输出的预测值；

Step 2 用损失函数计算预测值和标签值（真实值）之间的误差；

Step 3 计算损失函数的导数，根据梯度最小方向，反向修正前向传播中的权重；

Step 4 多次迭代，当损失函数值满足要求或迭代次数达到上限时，停止训练。

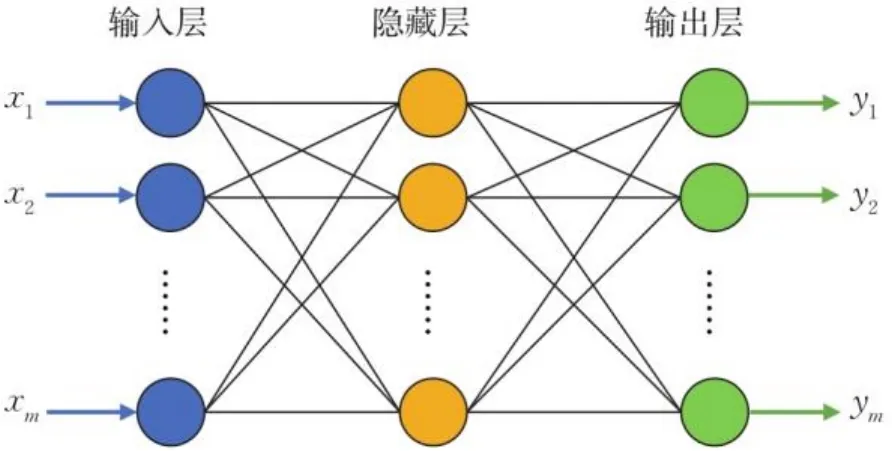
图1 FCNN结构Fig.1 The structure of FCNN

1.2 门控循环单元

RNN模拟了生物的循环反馈系统，由于能关联上下文信息，非常适合处理序列数据，其在自然语言处理、时间序列预测等领域大放异彩。但是，当序列较长时，标准RNN易出现梯度消失（gradient vanishing）或梯度爆炸（gradient exploding）等问题。

为解决上述问题，HOCHREITER等［18］引入了门机制，提出LSTM，在RNN基础上增加了3个门控（gate）单元，分别为遗忘门（forget gate）、输入门（input gate）、输出门（output gate），用于记忆之前的信息，但复杂的结构令网络训练成本升高。CHO等［19］对LSTM进行了优化，提出基于GRU的神经网络，门控单元由原来的3个变为2个，分别为重置门（reset gate）和更新门（update gate），从而提高了网络训练效率。

图2 GRU结构原理Fig.2 The structure principle of GRU

2 实例分析

2.1 研究区域及数据来源

长江流域覆盖19个省（直辖市、自治区），年平均水量达9 959×108m2，约占我国水资源总量的36%；单位面积（km2）水量约60×104m3，是全国平均值的2倍，充沛的水资源为我国地区社会经济的平稳发展提供了有力保障。国家地表水环境质量监测网在长江流域内设置了约500个监测断面，时刻关注其水质情况。本研究共涉及湖南长沙新港、湖南岳阳城陵矶、湖南益阳万家嘴、湖南常德沙河口、湖南常德坡头、湖南岳阳岳阳楼、湖北宜昌南津关、湖北武汉宗关、湖北丹江口胡家岭、江苏扬州三江营、江苏南京林山、重庆朱沱、河南南阳陶岔、安徽安庆皖河口、贵州赤水鲢鱼溪、江西九江蛤蟆石、江西九江河西水厂、江西南昌滁槎、四川乐山岷江大桥、四川广元清风峡、四川宜宾凉姜沟、四川攀枝花龙洞、四川泸州沱江二桥等23个水质监测站，共7 566条原始数据。

原始数据源自环保部环境监测总站地表水水质自动监测发布网站发布的2011—2018年水质监测数据，以周（w）为单位，对pH、溶解氧（DO）、高锰酸盐指数（CODMn）、氨氮（NH3-N）等4项水质指标进行预测。《地表水环境质量标准GB3838—2002》将水质从高到低划分为Ⅰ～Ⅴ类，其中包含对上述4项指标的评判标准，本研究所用数据集的最小值、最大值及对应评价标准如表1所示。

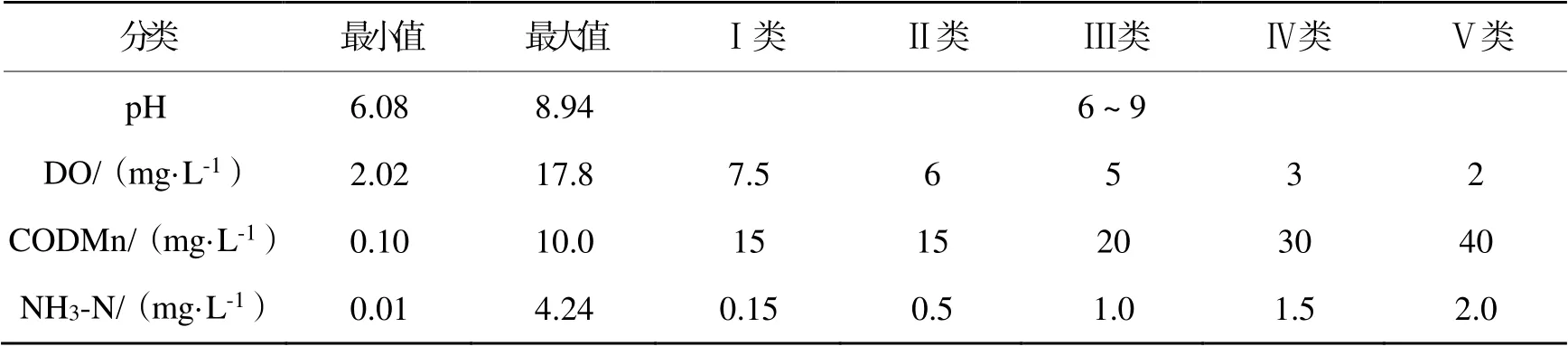
表1 《地表水环境质量标准GB3838—2002》中水质指数评价标准Table 1 Water quality index evaluation criteria of Environmental Quality Standard for Surface WaterGB3838-2002

2.2 数据预处理

由于数据集中个别指数空缺、部分周数据缺失，因此首先用线性插值法填补缺失数据。

接着，从上述样本数据集中随机抽取其中的80%作为训练集，10%作为验证集，10%作为测试集。

最后，基于训练集对输入数据进行标准化预处理，从而规范数据，提高神经网络的训练效率和模型精度。因为不同维度的输入指标具有不同的量纲和取值范围，数据间差异很大，若不进行标准化预处理，则会影响模型的运算结果。

本研究采用z-score标准化方法对原始水质指标进行预处理。z-score标准化也叫标准差标准化，依据原始数据的均值（mean）和标准差（standard deviation）进行计算，处理后的数据符合标准正态分布，即均值为0，标准差为1。计算式为

2.3 多元水质指标预测模型

基于预处理后得到的数据，设计GRU-FC复合神经网络。为提高模型梯度下降的效率与稳定性，集成小批量梯度下降（mini-batch gradient descent，MBGD）和自适应矩估计（adaptive moment estimation，ADAM）优化算法，构建多元水质指标预测（multivariate water quality parameter prediction，MWQPP）模型。MBGD与ADAM算法分别通过不同原理实现模型训练过程的优化。

MBGD算法将数据集划分为多个小批量（mini-batch）数据，一次只训练其中一个，这样可在每个mini-batch训练结束后更新权重和偏差，一代训练中可以调整多次，使梯度下降速度更快；同时由多个数据共同决定梯度的下降速度，训练过程较随机梯度下降法更稳定，不易产生大的振荡。本模型的mini-batch设置为64。

ADAM算法将动量（momentum）梯度下降算法与均方根传递（root mean square prop，RMSProp）算法相结合，其中动量用指数加权平均代替梯度，RMSProp用权重w和偏置b的梯度的微分平方加权平均代替梯度，以减少梯度下降过程中的摆动，加快逼近速度。

在模型结构上，MWQPP模型可分为输入层、多模块GRU层、并联FC层、输出层。

首先，将4项水质指标输入各自独立的GRU模块，模块内使用多层GRU，pH、DO、CODMn、NH3-N的GRU层数对应的单元数分别为（32，16）（32，8，4）（16，8）（64）。

其次，将4个GRU模块的输出数据进行并联操作，然后输入FC层，使用多层FC层模拟各水质指标之间的关系，调节模型的稳定性。共使用3层FC层，各层神经元个数分别为16，64，4，激活函数为缩放指数线性单元（scaled exponential linear unit，SELU），其中最后一层为输出层，用于输出目标时刻的水质指标预测值。

本模型以堆叠的方式组合各神经网络层，用均方误差（mean square error，MSE）作为损失函数。模型构建流程如下：

Step 1 对数据集进行筛选、标准化等预处理操作；

Step 2 根据选定的滑动窗口大小d，划分训练集、验证集、测试集；

Step 3 构建长江流域多元水质指标预测模型，设置相关超参数，初始化模型；

Step 4 训练预测模型，利用BP算法更新神经网络梯度，监测损失函数值，当其保持稳定时，自动停止训练；

Step 5 利用训练好的模型预测水质指标，计算各水质指标的模型评价指标。

模型整体结构如图3所示。

图3 多元水质指标预测（MWQPP）模型神经网络结构Fig.3 Neural network structure of MWQPP model

2.4 实验与分析

2.4.1 实验环境与设计

硬件环境：处理器Intel（R）Core（TM）i5-8300H CPU@2.30GHz，内存16.00 GB；软件环境：操作系统Microsoft Windows 10（64 bit）。使用Python API TensorFlow建立人工神经网络模型。

为借助其他研究成果验证本模型的有效性，实验还建立了多元线性回归（multiple linear regression，MLR）、随机森林（random forest，RF）［20］、FCNN［21］、LSTM［22］和CNN-GRU［17］水质预测模型，用于横向对比分析。

参考已有研究进行对比模型设计，并针对本研究样本数据进行调优。其中，RF模型中设置的决策树为100棵；FCNN模型包含了6层FC层，各层神经元数分别为32，64，128，64，8，4；LSTM模型包含双层LSTM循环神经网络，各层单元数分别为16和4；CNN-GRU模型包含二维卷积层与GRU层，过滤器维度为3，数量为1，GRU层单元数为64。

2.4.2 模型评价体系

用平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）、平均绝对百分比误差（mean absolute percentage error，MAPE）和决定系数（R2）等评价指标构建模型评价体系。各评价指标的计算式为：

2.4.3 误差评价

用所构建的MWQPP模型对验证集数据进行预测，以平均相对误差（mean relative error，MRE）指标为例，训练过程中模型的误差变化情况如图4所示。

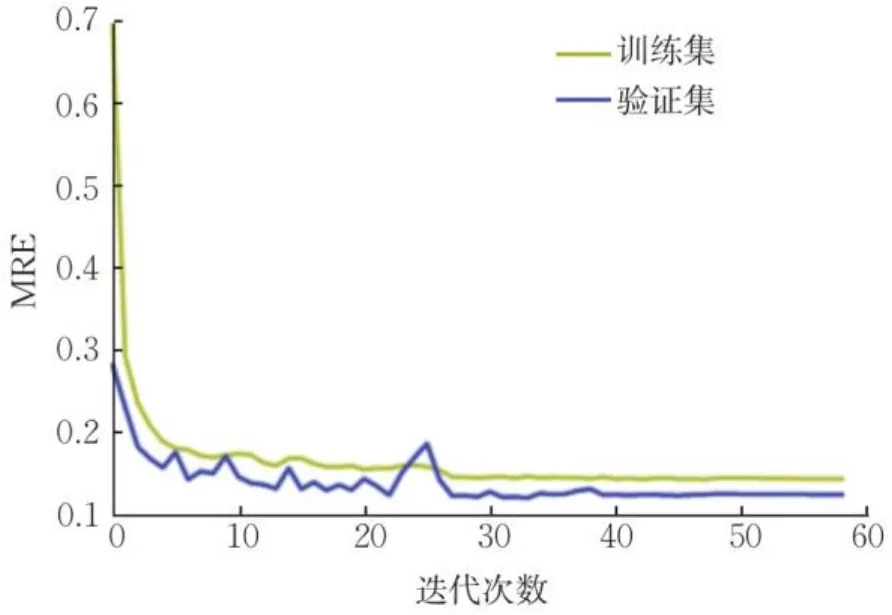
图4 训练过程MRE变化折线图Fig.4 MRE line chart of training process

同时，为进一步评价本模型的准确率与可靠性，选择部分当前常见的水质预测方法进行对比。考虑历史序列较短（8 w），预测范围较广，因此没有选择水质模拟模型和时间序列分析方法，而是选择了FCNN、LSTM、CNN-GRU、RF、MLR模型进行对比实验，横向比较6个模型的平均预测结果。表2列出了6个模型在pH、DO、CODMn、NH3-N水质指标上的误差评价结果。

表2 水质指标预测模型结果评价与比较Table 2 Result evaluation and comparison of water quality parameter prediction models

对预测结果进行反归一化处理，将预测结果缩放至真实量级，从而直观判断预测的实际误差。图5展示了某水质监测点位预测值与真实值的比较情况，横坐标为采样年份及周数，纵坐标为水质指标值。MWQPP模型对pH和DO这两项水质指标的预测精度较高，而对CODMn还有更进一步的提升空间。通过模型横向比较可知，MWQPP模型除pH的RMSE略大于MLR模型及pH的R2略小于MLR模型外，均较FCNN、LSTM、CNN-GRU、RF、MLR模型具有更小的MAE、RMSE、MAPE和更大的R2。计算MWQPP、FCNN、LSTM、CNN-GRU、RF、MLR模型的各指标平均MAPE，分别为0.130，0.200，0.140，0.138，0.155，0.144，可见MWQPP模型的精度至少提升了6%。

总之，从误差评估结果看，MWQPP模型的表现更均衡、更优良，在长江流域水质指标预测上的适用性更强。

2.4.4 鲁棒性评价

为验证模型的鲁棒性，即模型对数据的敏感性，随机挑选1个监测点位，以MAPE为误差指标，比较各模型在2011—2018年间每年的预测精度，并对比其预测误差的稳定性，结果如图6所示。可见，MWQPP模型的预测误差较稳定，而其他模型的预测误差更大，且误差波动更剧烈，这证明了MWQPP模型具有较好的鲁棒性。

图5 某点位水质指标各模型预测值与真实值比较Fig.5 Comparison of predicted values and true value at one certain point

同时，随机挑选10个监测点位，以MAPE为误差指标，比较各模型在不同点位上的预测误差，结果如图7所示。可见，MWQPP模型在不同点位上的预测误差较稳定，而其他模型在不同指标或点位上波动较大，这从另一角度证明了MWQPP模型的鲁棒性更好。

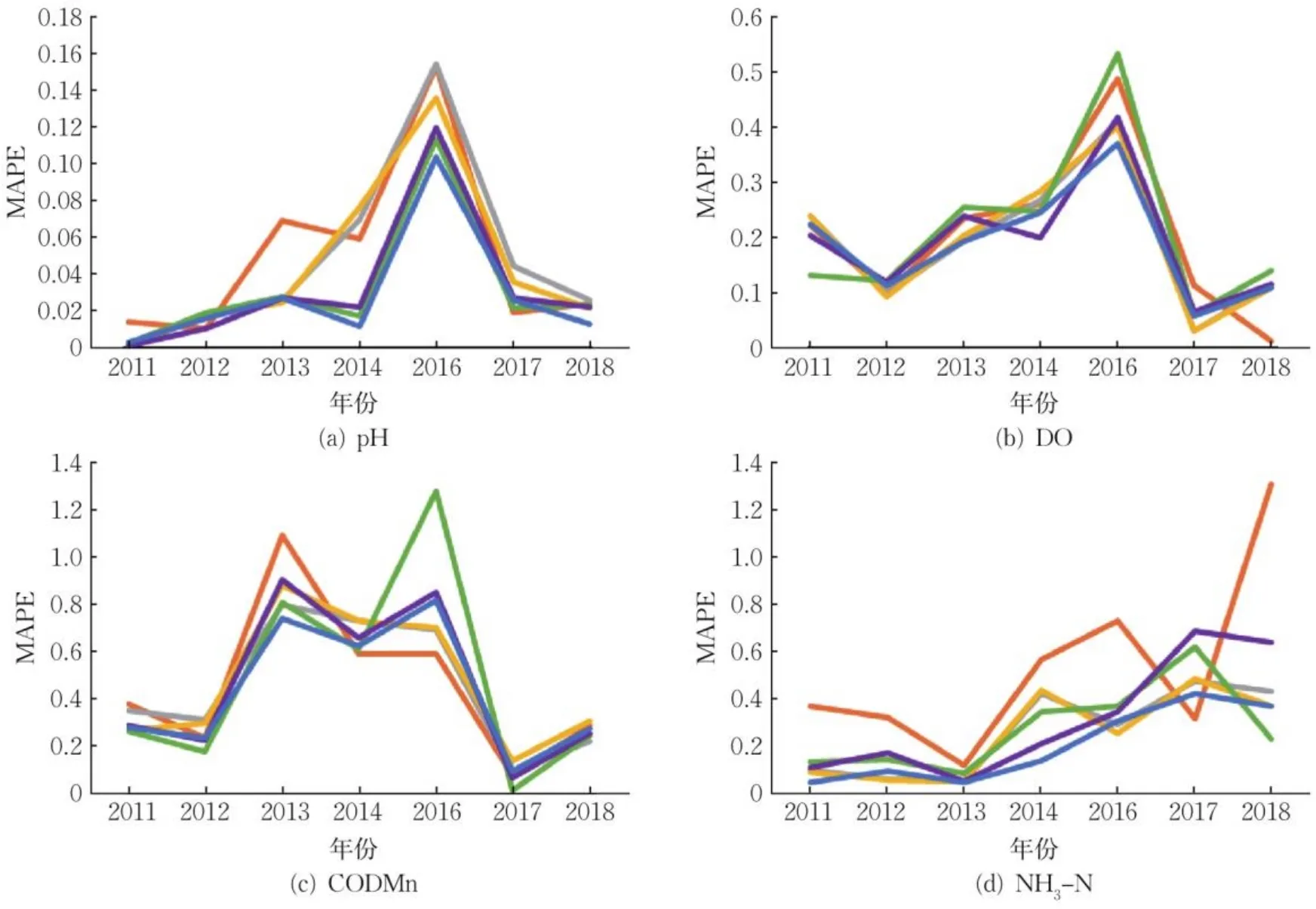
图6 某点位水质指标逐年预测MAPE比较Fig.6 Comparison of MAPE of each year at one certain point

图7 多点位水质指标预测MAPE比较Fig.7 Comparison of MAPE at several points

此外，对原测试集内3种不同比例的数据添加白噪声，形成3组新测试集。分别对原测试集的20%，40%，60%数据加入高斯白噪声，使用各对比模型进行预测与评价，用MAPE指标衡量各模型之间的鲁棒性差异，实验结果如表3所示。由表3可知，相较其他模型，MWQPP模型的噪声比例在20%～60%时，预测结果波动较小，MAPE小于0.02，且变化速率小，较稳定，可见MWQPP模型更为健壮，具有更好的抗噪性。

表3 不同噪声下各模型预测结果的MAPE对比Table 3 MAPE of different models under different noises

3 总结与展望

水质指标预测有助于把握水质的未来变化，该项工作有助于为长江流域水环境保护与水资源规划提供科学的决策依据，帮助相关部门针对性地制订水环境治理方案，为水资源保护与规划提供科学支持。

面向目前长江流域水质预测的现状，参考传统水质预测模型的优缺点，针对水质指标的非线性特点，基于人工神经网络理论，将GRU与FCNN相结合，提出了MWQPP模型。通过模型评价与横向比较，证明了MWQPP模型较FCNN、LSTM、CNN-GRU、RF、MLR模型能更均衡、更准确地预测长江流域pH、DO、CODMn、NH3-N等4项水质指标，且鲁棒性更佳，能较好地拟合水质指标数据的时间波动。

基于目前的研究趋势与工作成果，在对水质指标预测的进一步研究中，可考虑将神经网络与其他数据处理方法相结合，提高模型的预测性能，如在数据预处理时，对输入数据进行参数优化或分解重构，进一步提取数据特征；或结合机器学习等多种预测方法，构建复合预测模型；或引入注意力（attention）机制等新型人工神经网络方法，探索深度学习的更优实践方式。

［1］BERNHARD L， HØJSTRUP J. Evaluation of the wind-resource estimation program WAsP for offshore applications［J］. Journal of Wind Engineering and Industrial Aerodynamics，2001， 89（3/4）：271-291. DOI：10.1016/S0167-6105（00）00082-9

［2］MARTIN N， MCEACHERN P M，YU T， et al. Model development for prediction and mitigation of dissolved oxygen sags in the Athabasca River，Canada［J］. Science of the Total Environment，2013， 443：403-412. DOI：10.1016/j.scitotenv.2012. 10.030

［3］BAUWE A， ECKHARDT K U，LENNARTZ B. Predicting dissolved reactive phosphorus in tile-drained catchments using a modified SWAT model［J］. Ecohydrology and Hydrobiology， 2019，19（2）： 198-209. DOI：10.1016/j.ecohyd.2019.03.003

［4］秦文虎，付亚涛. 基于向量自回归模型的水质异常检测研究［J］. 安全与环境学报， 2018，18（4）： 1560-1563. DOI：10.13637/j.issn.1009-6094.2018.04.056

QIN W H， FU Y T. Water quality abnormity inspection and detection via the vector auto-regressive model［J］. Journal of Safety and Environment， 2018，18（4）： 1560-1563. DOI：10.13637/j.issn.1009-6094.2018.04.056

［5］CHEN W， XU H L，CHEN Z S， et al. A novel method for time series prediction based on error decomposition and nonlinear combination of forecasters［J］. Neurocomputing，2021， 426： 85-103. DOI：10.1016/j.neucom.2020.10.048

［6］马晋，何鹏，杨庆，等. 基于回归分析的地下水污染预警模型［J］. 环境工程， 2019，37（10）：211-215. DOI：10.13205/j.hjgc.201910036

MA J， HE P，YANG Q， et al. Early warning model for groundwater pollution based on regression analysis［J］. Environmental Engineering， 2019， 37（10）：211-215. DOI：10.13205/j.hjgc.201910036

［7］LI X， CHENG Z， YU Q， et al. Water-quality prediction using multimodal support vector regression： Case study of Jialing River， China［J］. Journal of Environmental Engineering， 2017，143（10）：04017070.

［8］白云，李勇. 基于VMD-LSSVR的河水水质预测方法［J］. 安全与环境学报， 2020，20（3）： 1162-1168. DOI：10.13637/j.issn.1009-6094.2019.0727

BAI Y， LI Y. A prediction model of the river water quality based on the VMD-LSSVR［J］. Journal of Safety and Environment， 2020，20（3）： 1162-1168. DOI：10.13637/j.issn.1009-6094.2019.0727

［9］薛同来，赵冬晖，韩菲. 基于GA优化的SVR水质预测模型研究［J］. 环境工程，2020， 38（3）：123-127，128. DOI：10.13205/j.hjgc.202003021

XUE T L， ZHAO D H，HAN F. SVR water quality prediction model based on GA optimization［J］. Environmental Engineering， 2020， 38（3）：123-127，128. DOI：10.13205/j.hjgc.202003021

［10］王晓萍，孙继洋，金鑫. 基于BP神经网络的钱塘江水质指标的预测［J］. 浙江大学学报（工学版）， 2007，41（2）： 361-364. DOI：10.3785/j.issn.1008-973X.2007.02.037

WANG X P， SUN J Y，JIN X. Prediction of water quality index in Qiantang River based on BP neural network model［J］. Journal of Zhejiang University（Engineering Science）， 2007，41（2）： 361-364. DOI：10.3785/j.issn.1008-973X.2007.02.037

［11］宓云軿，王晓萍，金鑫. 基于机器学习的水质COD预测方法［J］. 浙江大学学报（工学版），2008， 42（5）：790-793. DOI：10.3785/j.issn.1008-973X.2008.05.013

MI Y P， WANG X P，JIN X. Water COD prediction based on machine learning［J］. Journal of Zhejiang University（Engineering Science）， 2008，42（5）：790-793. DOI：10.3785/j.issn.1008-973X.2008.05.013

［12］SAMSUDIN M S， AZID A，KHALIT S I， et al. Comparison of prediction model using spatial discriminant analysis for marine water quality index in Mangrove Estuarine Zones［J］. Marine Pollution Bulletin， 2019，141： 472-481. DOI：10.1016/j.marpolbul.2019.02.045

［13］RAJAEE T， KHANI S，RAVANSALAR M. Artificial intelligence-based single and hybrid models for prediction of water quality in rivers： A review［J］. Chemometrics and Intelligent Laboratory Systems， 2020，200： 103978. DOI：10.1016/j.chemolab.2020. 103978

［14］TA X X， WEI Y. Research on a dissolved oxygen prediction method for recirculating aquaculture systems based on a convolution neural network［J］. Computers and Electronics in Agriculture， 2018，145： 302-310. DOI：10.1016/j.compag.2017.12.037

［15］NOORI N， KALIN L，ISIK S. Water quality prediction using SWAT-ANN coupled approach［J］. Journal of Hydrology， 2020，590： 125220. DOI：10. 1016/j.jhydrol.2020.125220

［16］WANG Z， MAN Y，HU Y， et al. A deep learning based dynamic COD prediction model for urban sewage［J］. Environmental Science （Water Research amp; Technology）， 2019，5（12）：2210-2218. DOI：10.1039/C9EW00505F

［17］TU J C， YANG X Q，CHEN C B， et al. Water quality prediction model based on GRU hybrid network［C］// 2019 Chinese Automation Congress （CAC）. Hangzhou： CAC，2019： 1893-1898. DOI：10.1109/CAC48633.2019. 8996847

［18］HOCHREITER S， SCHMIDHUBER J. Long short-term memory［J］. Neural Computation， 1997， 9（8）：1735-1780. DOI：10.1162/neco.1997.9.8.1735

［19］CHO K， VAN MERRIËNBOER B，BAHDANAU D， et al. On the properties of neural machine translation： Encoder-decoder approaches［EB/OL］.［2014-10-07］https：//arxiv.org/abs/1409.1259. DOI：10.48550/arXiv. 1409.1259

［20］BILALI A E， TALEB A，BROUZIYNE Y. Groundwater quality forecasting using machine learning algorithms for irrigation purposes［J］. Agricultural Water Management， 2021，245： 106625. DOI：10.1016/j.agwat.2020.106625

［21］刘世存，杨薇，田凯，等. 基于多层全连接神经网络的白洋淀水质预测［J］. 农业环境科学学报， 2020，39（6）： 1283-1292. DOI：10.11654/jaes.2020-0288

LIU S C， YANG W，TIAN K， et al. Water quality forecasting based on multilayer fully connected neural network for Baiyangdian Lake［J］. Journal of Agro-Environment Science， 2020，39（6）： 1283-1292. DOI：10.11654/jaes.2020-0288

［22］ZHOU J， WANG Y Y，XIAO F， et al. Water quality prediction method based on IGRA and LSTM［J］. Water，2018， 10（9）：1148. DOI：10.3390/w10091148

Multivariate water quality parameter prediction model based on hybrid neural network

WANG Yuwen1,2, DU Zhenhong1,2, DAI Zhen1,2, LIU Renyi1,2, ZHANG Feng1,2

（1. Zhejiang Provincial Key Lab of GIS，Zhejiang University，Hangzhou310028，China；2. Department of Geographic Information Science，Zhejiang University，Hangzhou310027，China）

The Yangtze River basin plays an important role in Chinese water resources allocation. What proves common knowledge is that it is particularly important to predict the water quality in the Yangtze River basin. Based on the existing research, the recurrent neural network (RNN) model with gate recurrent unit (GRU) and fully connected neural network (FCNN) are combined in this study to improve a multiple water quality parameter prediction (MWQPP) model. It is proposed to predict the four water quality parameters, such as pH, dissolved oxygen (DO), permanganate index (CODMn) and ammonia nitrogen (NH3-N) in the Yangtze River basin. Based on 7 566 raw data of 23 water quality monitoring points in the Yangtze River basin from 2011 to 2018, the comparative experiments show that the root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE) and coefficient of determination (R2) obtained from the MWQPP modelapos;s prediction results are better than traditional models, such as the multiple linear regression model, the random forest model, FCNN model and LSTM model, and the MWQPP model also has better robustness than these traditional water quality prediction models. As we can say, the MWQPP model can provide scientific, reasonable and effective support for water quality assurance and water management in Yangtze River basin.

water prediction; artificial neural network; gate recurrent unit (GRU); fully connected neural network(FCNN)

P 208

A

1008⁃9497（2022）03⁃354⁃09

10.3785/j.issn.1008-9497.2022.03.013

2021⁃01⁃14.

国家自然科学基金资助项目（41922043，41871287，42001323）；国家重点研发计划项目（2018YFB0505000）.

王昱文（1996—），ORCID：https：//orcid.org/0000-0003-1119-7120，女，硕士研究生，主要从事时空大数据挖掘研究.

通信作者，ORCID：https：//orcid.org/0000-0001-9449-0415，E-mail：duzhenhong@zju.edu.cn.