基于慢特征分析方法研究陆地表面气温变率的驱动力
朱丽飞 孙诚 李建平 张静 刘雨森 宫湛秋
1 北京师范大学全球变化与地球系统科学研究院, 北京100875
2 中国海洋大学物理海洋教育部重点实验室/海洋高等研究院/深海圈层与地球系统前沿科学中心, 青岛266100
3 青岛海洋科学与技术国家实验室海洋动力过程与气候功能实验室, 青岛266237
1 引言
19 世纪末以来,全球平均表面温度(GMST,Global Mean Surface Temperature)呈现出百年尺度的增暖趋势,并且自1970 年代以来增温趋势明显加快(IPCC, 2007)。全球表面温度普遍升高,但由于下垫面热力性质的不同存在差异。陆地区域的变暖速率一般要快于海洋。在1880~2018 年期间,全球平均陆地表面气温(LSAT, Land Surface Air Temperature)增加了1.41°C,而同期全球平均表面温度上升了0.86°C(IPCC, 2013)。全球陆地的变暖也存在区域差异,20 世纪以来,相比于南半球,北半球的增温起始时间早,增温速度快,扩展范围广(Ji et al., 2014)。这种全球百年尺度的增温趋势与辐射强迫有关,主要原因是大气层中温室气体浓度的变化,尤其是人类活动导致的CO2浓度增加所引起的温室效应的加剧(Wild, 2016)。
在1951~2012 年期间,全球平均表面温度(GMST)每10 年增长0.12°C,但在1998~2012年期间,全球平均地面增温速率减缓,出现了气候变暖暂时的“停滞”(宋斌等, 2015; 林霄沛等,2016; 苏京志等, 2016; 徐一丹等, 2019)。一些研究表明气候系统内部的自然变率对温度变化趋势有重要的调节作用(Wu et al., 2011; 徐一丹等, 2019)。在年际时间尺度上,热带太平洋的厄尔尼诺—南方涛动(ENSO, El Niño-Southern Oscillation)现象对全球平均温度有重要的影响(Lin and Qian, 2019)。在年代际时间尺度上,太平洋年代际振荡(IPO/PDO, Interdecadal Pacific Oscillation/Pacific Decadal Oscillation)表现出与ENSO 空间结构相类似的特点(朱益民和杨修群, 2003; 杨修群等, 2004)。全球变暖减缓时期,海表温度(SST, Sea Surface Temperature)呈现异常的空间分布格局,主要表现为热带东太平洋海表温度持续冷却(Kosaka and Xie, 2013),这一现象与ENSO 循环中拉尼娜冷事件以及PDO 的冷位相有关(刘珊等, 2019)。除了太平洋,大西洋对全球平均温度的变化也有重要贡献(Sutton and Hodson, 2007)。通过年代际海气动力耦合的作用,北大西洋涛动(NAO, North Atlantic Oscillation)超前北大西洋海温多年代际振荡(AMO, Atlantic Multidecadal Oscillation)和北半球平均温度(NHT, North Hemisphere Temperature)15~20 年,20 世纪90 年代开始的NAO 年代际减弱对后期的全球变暖减缓有重要贡献(龚道溢等,2001; Sun et al., 2015; 苏京志等, 2016)。这种年代际尺度的超前关系可以用大气强迫对海洋环流的累积效应来解释。此外,有学者利用旋转经验正交函数(REOF, Rotated Empirical Orthogonal Function)的方法研究GMST 的变率,发现大西洋通过AMO对GMST 的年代际变率贡献最大,而太平洋地区主要通过ENSO/PDO 及其遥相关,太平洋海温变率对GMST 的贡献相比大西洋要小的多,并且发现AMO/PDO/ENSO 三个海温模态加上长期趋势后可以很好地拟合全球平均海温(Global Sea Surface Temperature)(Chen and Tung, 2018),并被视为重要的海洋变率。尽管辐射强迫和气候系统内部变率对全球气温的变化有显著影响,但在区域尺度上不同因子的作用差异还有待进一步阐明。
气候模式模拟的结果表明全球和区域尺度温度的变化是外部辐射强迫和气候内部变率相互作用的产物(Meehl et al., 2013; Yu et al., 2020; Xiao et al.,2020)。气候系统是一个复杂的非线性系统,其背后的物理机制有时很难解释。气候系统变化的驱动力和因果关系分析是气候动力学的一个基本问题。不同领域的研究者已经提出了一些新的方法来研究动力系统的驱动力,这些方法能够将隐含在观测或模拟的非平稳时间序列中的驱动力提取出来。具有代表性的方法主要有:Granger 因果关系、条件互信息和转移熵、收敛交叉映射(CCM, Comvergent Cross Mapping)(Granger, 1969; Schreiber, 1997;Sugihara et al., 2012; Tsonis et al., 2015)以及慢特征分析(SFA, Slow Feature Analysis)(潘昕浓等,2016, 2017)。SFA 可以从快速变化的动力系统中提取缓慢变化的驱动力,能够有效地估计系统内在的驱动力(Wiskott, 2003; Konen and Koch, 2011)。其优势是不需要了解所研究系统的具体的数学模型,利用长期的观测数据,可以直接提取观测数据背后的驱动力,并且该方法可以有效地克服随机噪音的干扰。该方法最初是在神经生物学领域发展起来的,后来推广到物理、工程学和气候变化等其他领域。已有研究利用SFA 方法和小波分析,重建了北半球月平均地表气温异常时间序列的驱动力,发现该驱动力包括两个独立的自由度,分别与22 年太阳活动周期和AMO 气候变率有关 (Yang et al., 2016)。随后,有学者提出了一种在平稳区域对非平稳系统产生影响的情况下重构驱动力的新方法(Zhang et al., 2017),且数值分析表明,原始和重构驱动力之间的相关系数可以达到0.97,后利用该方法应用在北半球月平均地表气温时间序列中,结果同样证明其基本强迫周期与太阳黑子和AMO 的周期一致。也有学者基于最长仪器观测的英格兰中部温度CET 数据集,同样结合SFA 方法和小波分析,得出气候变化的驱动力有3.36 和22.6 两个自由度,它们分别与ENSO 生命周期和太阳黑子循环周期有关(Wang et al., 2017)。另有研究在中欧LSAT的站点观测数据基础上提取驱动力,发现其与NAO 有显著正相关关系(Wang et al., 2019)。
已有研究结果表明SFA 方法在提取非平稳系统的慢变驱动力以及研究长期气候变化的驱动因子等方面有非常明显的优势。以往利用SFA 提取非平稳系统慢变驱动力的研究多是针对某个区域平均的时间序列(Schreiber, 2000; Yang et al., 2016;Zhang et al., 2017; 范开宇等, 2018; Tsonis et al.,2019; Zhang et al., 2019)。一维时间序列的分析方法在分析包含时—空协同演变信息的多维数据方面有局限性(胡淑娟, 2006; 刘海涛等, 2007; 胡淑娟等, 2020)。由于不同地区气候的慢变驱动力在时间演变上并不一致,在全球范围内,不同地区气候慢变驱动力之间的关系以及全球气候慢变驱动力的空间结构差异,这些问题还尚未得到较好的解释,所以有必要对不同空间尺度上的慢变驱动力进行诊断。以LSAT 为例,从多维时空角度在全球范围内提取LSAT 的慢变驱动力,为理解全球气温慢变驱动力的空间特征提供了思路。基于此,将SFA 方法拓展到时空三维的LSAT 场中,包括时间、经度、纬度三个维度,在全球范围内提取LSAT 的慢变信号。具体来说,就是将格点资料中每个格点的LSAT时间序列首先进行独立的SFA 分析,而后再从全球范围对LSAT 慢变驱动力的空间特征进行整体分析。
本文将过去100 多年来观测记录的原始气温场提取的慢变驱动力信号分别与全球辐射强迫(GRF,Global Radiation Forcing)、 AMO、 PDO 和Niño3.4 气候指数进行相关分析,与原始观测结果做对比,并选择显著区域平均LSAT 的驱动力进行分析。通过分析GRF 和不同气候指数对全球观测LSAT 异常以及气候系统慢变驱动力的影响,证明气候外部强迫与内部变率(主要是海洋内部变率)对LSAT 的重要影响。最后为了验证结果的可靠性,使用模式模拟结果来验证GRF 与三大气候指数对LSAT 的重要影响。
文章第二部分介绍数据来源与研究方法;第三部分介绍LSAT 观测数据与SFA 方法提取的慢变驱动力分别与GRF、AMO、PDO、Niño3.4 气候指数做相关分析的结果;第四部分介绍模式验证得到的结果。第五部分介绍了本研究得到的主要结论和引发的讨论。
2 数据与方法
2.1 数据来源与介绍
全球逐月陆地表面气温数据来自物理科学实验室(PSL, Physical Sciences Laboratory)特拉华大学气温与降水数据集(University of Delaware Air Temperature & Precipitation)V3.01 版本https://psl.noaa.gov/data/gridded/data.UDel_AirT_Precip.html[2020-05-22]。该数据为格点数据,包括1900~2010 年全球气温和降水高分辨率站点(陆地)月数据。哥特华大学的Cort Willmott 和Kenji Matsuura收集了大量来自GHCN2(全球历史气候网络)和公共档案的数据。数据集覆盖全球包括南极洲在内的陆地,补充了国际海洋大气综合数据集(ICOADS)。文中使用该数据集中的逐月陆地表面气温数据,且与影响因子做相关分析时未做任何滤波或者平滑处理。
AMO、PDO、Niño3.4 逐月海温指数来源于世界气象组织下属的气象数据检索平台Climate Explorer( http://climexp.knmi.nl/selectindex.cgi?id=someone@somewhere [2020-05-22])。
AMO 是北大西洋SST 模态的主要信号,在50~70 年波段具有显著的波谱峰值。有关研究表明,AMO 是影响区域至半球尺度气候的气候系统内部变率。本研究中AMO 被定义为北大西洋地区赤道以北至极地(0°~60°N,0°~80°W)的海温减去60°S~60°N 区域海面平均温度,数据来源于NCDC 的ERSST V5 数据集。
ENSO(El Niño、La Niña 和南方涛动)被认为是热带太平洋上一种自然的海洋—大气耦合模态(Deser et al., 2010),对全球的气候有重要的影响(Newman et al., 2003)。本研究中采用Niño3.4 指数表示ENSO 事件,定义为HadSST1 数据集分析得 到 的 Niño3.4 区 域( 5°N~5°S, 170°W~120°W)范围内的平均海表温度异常,正值代表El Niño,负值代表La Niña。
太平洋年代际涛动(Pacific Decadal Oscillation,PDO)是北太平洋区域海温的主导模态,其相位的变化可以影响北太平洋甚至是北半球大气环流的变化。PDO 处于正位相时,北太平洋海水变冷,负位相则反之。本文中PDO 指的是北太平洋地区20°以北逐月海表温度异常正交函数分解第一模态(EOF1)的时间序列(Mantua et al., 1997; Kosaka and Xie, 2013)。Messié and Chavez(2011)对全球SST 异常进行EOF 分解,发现全球SST 年际到年代际尺度的变率主要由ENSO、AMO 和PDO 三个海温模态所主导(解释方差合计接近30%)。因此,本文分析的AMO、ENSO 和PDO 三个海温模态在时间和空间是相对独立的。
全球辐射强迫数据来自于CMIP5 GISS-E2 Global Radiative Forcing (Fi) Data (Miller et al.,2014;https://data.giss.nasa.gov/modelforce/[2020-05-22])。其是以年为单位的连续辐射强迫。辐射强迫包括太阳辐射、温室气体、火山活动、臭氧、气溶胶、土地利用变化等辐射传输总和,也叫全球总辐射强迫,用GRF 表示,在这里代表气候系统的大部分外部因素。
2.2 方法
SFA 方法能够提取非线性平稳系统的慢变驱动力信号。其是将实际观测数据嵌入到m维的空间里,进行一系列的变换与重组,利用最小二乘法求出数学模型的常数,进而提取慢特征变量,得到系统的驱动力。对于未知动力系统的给定时间序列{x(t)}t1,···,tn,这里t表示时间,n表示时间序列的长度,SFA 算法的基本步骤如下:
(1)将{x(t)}嵌入到一个m维状态空间中,进行空间重构,

式中k=m+m(m+1)/2。
(3)将公式(3)统一到一个球面上,生成零均值、单位协方差的坐标分量,即


以上是提取驱动力步骤的简单介绍,具体可以在Yang(2016)和范开宇等(2018)的文章中找到。值得注意的是:如果一个驱动力包括多个成分,系统本身的可预测性和嵌入维数m的大小可能会改变提取结果(Konen and Koch, 2009, 2011)。
数据处理过程:对逐个格点上的LSAT 原始序列去除年循环,然后设置嵌入维度数m为13(对应的驱动力分辨率为一年)(Yang et al., 2016; 潘昕浓等, 2016),时滞参数τ为1,利用SFA 方法,将资料中每个格点的LSAT 时间序列首先进行独立的SFA 分析,提取其慢变驱动力;而后从全球范围对LSAT 慢变驱动力的空间特征进行整体分析。此外,SFA 提取的外强迫和实际外强迫相差一个放大因子和平移系数 (Wang et al., 2011) ,因此本文重点探讨SFA 提取的外强迫和实际外强迫之间相关性的强弱。
2.3 模式模拟
历史海温驱动的AGCM 试验,即AMIP(Atmospheric Model Intercomparison Project),其根据海表温度和海冰数据反演出真实的大气辐射强迫,是一个专门为大气环流模式所设计的试验计划(冯娟和李建平, 2012; 安然等, 2019),同时也是全球大气环流模式的标准输出实验协议。它为从事全球气候模式的诊断分析、验证、比较和数据交流提供了一个基本平台。AMIP 模型配置能够使研究更加专注于大气模型,而不会增加气候系统中海洋—大气反馈的复杂性,可以说是一个“理想的海洋”。该模式综合了10 个集合的平均结果,可以大大减少大气内部过程对LSAT 的影响,从而保留了辐射和海温等外强迫对LSAT 的影响。模拟试验过程中的外部辐射强迫部分,采用观测(记录)到的太阳活动和大气成分变化(包括温室气体、气溶胶和火山气溶胶)来驱动所有的历史强迫实验(Xu et al., 2020)。CAM5(Community Atmosphere Model 5)是CESM 的大气模式,依托美国国家海洋大气局(NOAA)地球系统研究实验室(ESRL)平台,用AMIP 观测辐射通量做强迫来模拟全球表面温度。所以,模式的结果很大程度上能够反映LSAT 的慢变驱动力。
本文使用该模式输出的百年尺度LSAT 与GRF、AMO、Niño3.4 和PDO 指数进行相关分析。在没有海洋—大气反馈的作用下,分析LSAT 发展变化的内部驱动机制,得出LSAT 不仅受外辐射强迫,还受年际以及年代际SST 自然变率的影响。模式结果再现了LSAT 的观测结果,验证了其受到GRF、AMO、Niño3.4、PDO 的区域影响。
3 结果与分析
本文利用SFA 方法探讨了LSAT 的慢变信息,我们所使用的是1900~2010 陆地气温的观测资料,时间分辨率为逐月。因此,利用SFA 方法提取的LSAT 慢变信号在时间尺度上主要包含了年际和年代际尺度等低频信号。结果发现,较原始观测数据,使用SFA 方法提取的全球LSAT 的慢变驱动力时间序列,与GRF、AMO、Niño3.4 和PDO 指数的相关性有了很大的提高,这进一步证明LSAT 不仅受到外部强迫作用,还受到海洋作用的显著影响。
3.1 全球辐射强迫对LSAT 的影响
地球从自身以外获取能量的主要途径是太阳辐射,可以说太阳辐射是地球表面热量的主要能量来源。自工业革命以来,全球温室气体浓度不断增加,全球地表温度也随之上升。目前已有大量关于温室气体浓度增加导致全球增温及其内部物理机制的研究(Kang et al., 2010)。本文重点是从全球辐射强迫和海洋作用的角度来分析地表增温的时空特征。总辐射强迫空间分布图显示,在全球大部分地区是增加的趋势,只有在东南亚地区和北美中部地区是下降趋势(Miller et al., 2014)(图略)。
需要说明的是,SFA 方法由于受到嵌入维度m和时滞参数τ的制约,提取出的慢变驱动力的始末年份可能失真,故在提取结果中删除了始末年份,保留1901~2009 年的驱动力结果。为使结果具有可比性,统一选取1901~2009 年时间段的观测LSAT、GRF 和三大SST 模态进行分析。
图1a 表明,GRF 对全球大部分地区观测LSAT存在普遍影响,例如非洲、南美洲北部和东部、欧亚大陆东南部、南极洲大部分地区、格陵兰岛东部和澳洲中部地区。在这些地区,区域平均LSAT与GRF 的相关系数都在0.5 以上。不同的是,南极洲东半球部分区域LSAT 受到GRF 的异常影响。图1b 显示,与观测结果相比,SFA 方法提取的慢变驱动力与GRF 的相关系数明显增大,特别是欧亚大陆中部、非洲中部和南极洲地区。GRF 可能在很大程度上影响甚至决定LSAT,甚至说GRF是LSAT 的重要慢变驱动力之一。为了进一步探究LSAT 和GRF 的关系,文中选择两个显著相关地区,即欧洲中部地区(30°~60°N,30°~60°E)和北非地区(0°~30°N,0°~30°E)的区域平均LSAT 和GRF 进行具体分析。由于文中使用的GRF数据是以年为单位,相应地对1901~2009 年LSAT 和驱动力时间序列求年平均,将其转化成以年为单位的数据,再进行相关分析。
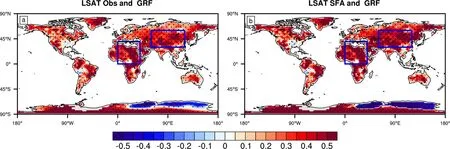
图1 1901~2009 年(a)观测LSAT、(b)SFA 方法提取的LSAT 慢变驱动力与逐年GRF 的相关系数的空间分布。蓝色方框内为相关系数显著增加的区域,分别为北非地区(0°~30°N,0°~30°E)、欧亚大陆中部地区(30°~60°N,30°~60°E)。黑色打点区域代表通过95%的信度水平检验Fig. 1 Correlation of (a) the original observed LSAT(Land Surface Air Temperature) and (b) the LSAT slow driving force extracted by the SFA(Slow Feature Analysis) method with the annual GRF(Global Radiation Forcing ) for 1901-2009. In the blue boxes, the regions with significantly increased correlation coefficients are Central Eurasia (30°-60°N, 30°-60°E) and North Africa (0°-30°N, 0°-30°E). Regions above 95% confidence level are black spotted
欧亚和非洲作为世界上最大的两个大陆,其在一定程度上可以代表大陆LSAT 的发展趋势。图2显示,中欧和北美大陆LSAT 与GRF 显著相关,1901~2009 年期间,GRF 呈现增加的趋势,特别是自工业革命时代二十世纪七十年代以来,全球辐射强迫增加迅速,同样LSAT 也呈现快速上升的趋势,这与全球变暖的大背景一致。表1 显示,二者的相关性十分显著,欧洲中部地区观测LSAT 与GRF 的相关系数为0.58,SFA 提取的慢变驱动力信号为0.71,解释方差增长17%;北非地区观测LSAT 和SFA 提取的慢变驱动力与GRF 的相关系数分别是0.64 和0.70,而解释方差相差8%。以上结果表明,SFA 提取的慢变驱动力与GRF 的相关性明显增强。而且,在1901~2009 年期间,GRF出现四次显著下降(红色实线向下尖端),在每次总辐射突然下降后不久,LSAT 也出现下降的现象。这也进一步说明GRF 对LSAT 有显著影响。

表1 区域平均的LSAT 与逐年GRF 的相关系数和解释方差Table 1 Correlation coefficient and explanatory variance of the regional mean LSAT and the annual GRF
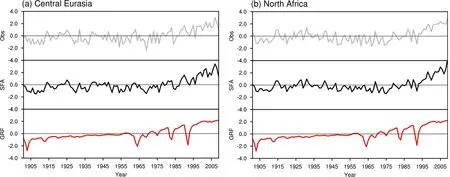
图2 1901~2009 年(a)欧亚大陆中部地区(30°~60°N,30°~60°E)、(b)北非地区(0°~30°N,0°~30°E)区域年平均LSAT 与逐年GRF 的标准化时间序列。红线表示GRF,灰线表示观测LSAT,黑线表示SFA 方法提取的LSAT 慢变驱动力Fig. 2 Normalized time series of the regional mean annual LSAT in (a) Central Eurasia (30°-60°N, 30°-60°E) and (b) North Africa (0°-30°N,0°-30°E) and annual GRF for 1901-2009. The red lines represent the annual GRF. The gray line represents the original observed LSAT. The black line represents the LSAT slow driving force extracted by the SFA method
3.2 AMO 对LSAT 的影响
相关研究表明,AMO 作为气候系统的内部变率之一,对区域和半球尺度的气候都有影响(Knight et al., 2006; Zhang et al., 2007; 杨韵等,2018),特别是北半球平均LSAT 和北极海冰异常的多年代际变化。有学者研究证明,北大西洋海温对北半球SAT 有重要调控作用。观测和数值模拟试验表明,在年代际尺度上,AMO 可以影响北半球大部分地区LSAT,其年时间序列的波峰与去趋势后的北半球地表温度的波峰变化在很大程度上是同步的(Li et al., 2013)。有研究利用经验正交函数分析(EOF , Empirical Orthogonal Function)得出LSAT 的EOF4 与AMO 有显著相关性,EOF4能够解释LSAT 的年代际变化,特征区域主要集中在北半球(Dai et al., 2015)。AMO 作为接近最大时间尺度的气候内部自然变率,对全球地表温度有显著的影响。将全球LSAT 的观测数据和驱动力时间序列分别与AMO 指数做相关,以此来进一步分析AMO 对全球LSAT 的影响。
如图3a 所示,AMO 与北半球大部分陆地表面气温显著相关,如大西洋周边和东亚地区。图3b中SFA 提取的慢变驱动力与AMO 有更强的相关性,在低纬度地区和北半球中高纬度地区表现十分明显,尤其是北大西洋周边地区(格陵兰岛、北美洲东南部)、东亚、南美洲和非洲部分地区。
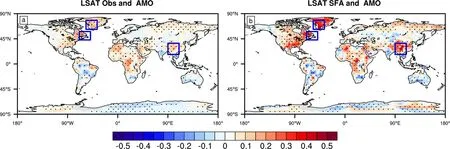
图3 同图1,但为1901~2009 年(a)观测LSAT、(b)SFA 方法提取的LSAT 慢变驱动力与逐月AMO 指数的相关系数的空间分布。蓝色方框区域分别为东亚地区(17°~37°N,90°~110°E)、北美洲东部(43°~63°N,49°~69°W)和格陵兰岛地区(58°~78°N,37°~57°W)Fig. 3 As in Fig. 1, but for correlation of (a) the original observed LSAT and (b) the LSAT slow driving force extracted by the SFA method with the monthly AMO (Atlantic Multidecadal Oscillation) index. The blue boxes represent East Asia (17°-37°N, 90°-110°E), eastern North America(43°-63°N, 49°-69°W), and Greenland (58°-78°N, 37°-57°W)
AMO 通过“大气桥”和“海气耦合桥”影响下游欧亚大陆气候(Li and Bates, 2007; Wang et al.,2009; 李双林等, 2009, 2015; 罗菲菲和李双林,2015)。有研究表明AMO 和东亚地区(具体区域范围:20°~40°N,90°~120°E)LSAT 在同期达到最大相关,年均值相关系数达到0.6 以上,且证明AMO 可能通过西向波列影响东亚表面温度(Xie et al., 2019)。
AMO 还可能通过海洋—大气之间的耦合作用影响周边地区LSAT。有研究表明,北美大陆的冬季增温与AMO 正位相期间出现的两个低压异常中心有关,欧洲大陆夏季温度正异常可能与北大西洋暖海温有关(Sutton and Hodson, 2005, 2007)。此外,还有研究表明AMO 对大西洋周边地区(北美洲东北部、格陵兰岛、冰岛)的热通量和LSAT 有显著相关关系,并且利用信息流理论的因果方法证明AMO 是后两者的因(Gong et al., 2020)。
月尺度分辨率的AMO 与对应时间分辨率的观测LSAT 之间的相关系数并不大,最大相关系数不超过0.3,而利用SFA 方法提取的LSAT 慢变驱动力信号与AMO 的相关系数可以达到0.44。这也进一步说明AMO 对LSAT 有着重要的影响。本文列出三个显著相关区域,分别是东亚地区(17°~37°N,90°~110°E)、北美洲东部(43°~63°N,49°~69°W)、和 格 陵 兰 岛 地 区(58°~78°N,37°~57°W)LSAT 与AMO 的时间序列,以进一步探究AMO 对局地LSAT 的影响。
图4 显示,在年代际尺度上,AMO 指数在1901~2009 年期间存在一个“负—正—负—正”的位相变化,而三个地区的LSAT 也出现了这样的变化特征。在1925~1945 年,AMO 处于正位相,而LSAT 高于平均温度,出现变暖。并且,在1901~1920 年和1990~2009 年LSAT 和AMO 的峰谷变化基本一致,但是在观测LSAT 时间序列中,由于许多天气噪音干扰,这种变化特征并不明显。特别是从长达百年的时间维度上可以看出,SFA 提取的LSAT 慢变信号和AMO 在多年代际尺度上存在着十分密切的联系。并且,相比于观测数据,SFA提取的慢变驱动力信号与AMO 的相关系数显著增大,解释方差也有明显增加。
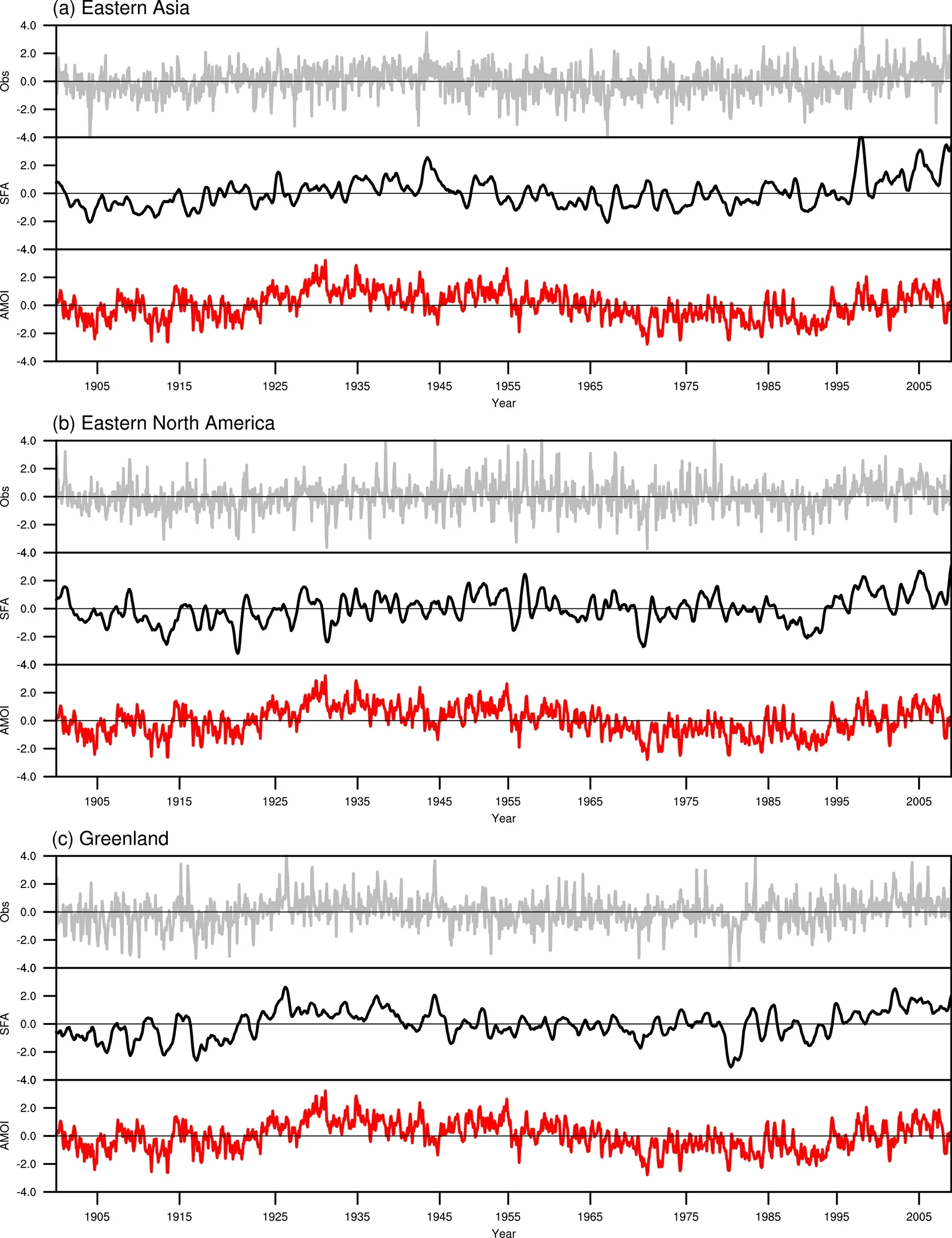
图4 同图2,但为(a)东亚地区(17°~37°N,90°~110°E)、(b)北美洲东部(43°~63°N,49°~69°W)、(c)格 陵兰岛地区(58°~78°N,37°~57°W)区域月平均LSAT 和逐月AMO 指数。红线表示逐月AMO 指数,灰线表示观测LSAT,黑线表示SFA 方法提取的LSAT 慢变驱动力Fig. 4 As in Fig. 2, but for the regional mean monthly LSAT in East Asia (17°-37°N, 90°-110°E), eastern North America (43°-63°N, 49°-69°W),and Greenland (58°-78°N, 37°-57°W) and the monthly AMO index(AMOI). The red lines represent the monthly AMOI. The gray line represents the original observed LSAT. The black line represents the LSAT slow driving force extracted by the SFA method
东亚地区与大西洋地区虽未毗邻,但是它们之间却存在着重要联系。表2 显示,东亚地区平均LSAT 观测时间序列与AMO 的相关系数只有0.13,但是SFA 提取的慢变驱动信号与AMO 指数的相关系数可以达到0.33,解释方差也增加了9%,并且在多年代际尺度上总体变化趋势和峰谷的位置基本一致。可见,SFA 方法能够有效地去除数据中的天气噪音信号,能够真实体现陆地温度的驱动力信号。
图3 表明AMO 对北美洲东部和格陵兰岛这些大西洋周边地区有很大的影响。曾有研究通过气候模式模拟得出,大西洋通过重新分配内部海洋的热量可以产生类似于观测的多年代际变率,而AMO作为内部海洋变率,可以作为北半球温度多年代际变率的可靠解释(Sutton and Hodson, 2007)。AMO通过影响海洋以及沿海陆地的热通量,进而影响北大西洋沿岸地区LSAT 变化。表2 显示,北美洲东部、格陵兰岛地区平均LSAT 时间序列与AMO 的相关系数分别为0.25 和0.18,而SFA 提取出的驱动力与AMO的相关系数则分别达到0.44 和0.39,解释方差分别增加13%和12%。这进一步证明AMO 可能是大西洋周边地区LSAT 多年代际变率的驱动力之一。

表2 同表1,但为逐月AMO 指数Table 2 As in Table 1, but for the monthly AMO index
AMO 对北半球LSAT 有显著的影响,主要集中在大西洋周边(北美洲东北部、格陵兰岛)、亚洲东南地区和非洲部分地区。在选择的三个地区中,SFA 提取的LSAT 慢变驱动力与AMO 的相关性显著提高,解释方差明显增长,进一步证明AMO对LSAT 有显著影响。
3.3 El Niño 对LSAT 的影响
在典型的El Niño 年,赤道太平洋东西海温出现异常,温度、气压梯度减小,赤道东风减弱,Walker 环流减弱,对流旺盛区和上升支东移,Hadley 环流相应减弱,西太平洋副热带高压的位置比往年偏南,西太平洋地区由于对流减弱,往往更加干旱;而东亚地区季风出现异常,进而引起LSAT 出现变化。强El Niño 年还能引起北太平洋和北美地区大气环流的变化,冬季盛行期间阿留申低压和“太平洋—北美”PNA(Pacific-North America)大气遥相关型的500 hPa 位势高度出现异常(马杰, 2007),进而导致北美洲温度发生异常变化。
图5a 显示,全球大部分地区LSAT 与Niño3.4指数显著相关,特别是太平洋周边和低纬度地区,包括澳洲部分地区。具体来说,北美洲北部、东南亚部分地区、南美洲、非洲、印度次大陆和澳洲地区的LSAT 与Niño3.4 指数具有一致显著的相关关系,欧洲东北部、北美洲南部和南极洲部分地区则呈现显著且一致的相关性。图5b 显示,在北美洲、印度次大陆、南亚地区、非洲和澳洲等地区,SFA 提取的慢变驱动力与Niño3.4 指数的相关系数的绝对值明显增大,进一步证明ENSO 对这五大地区的LSAT 有很大的影响。
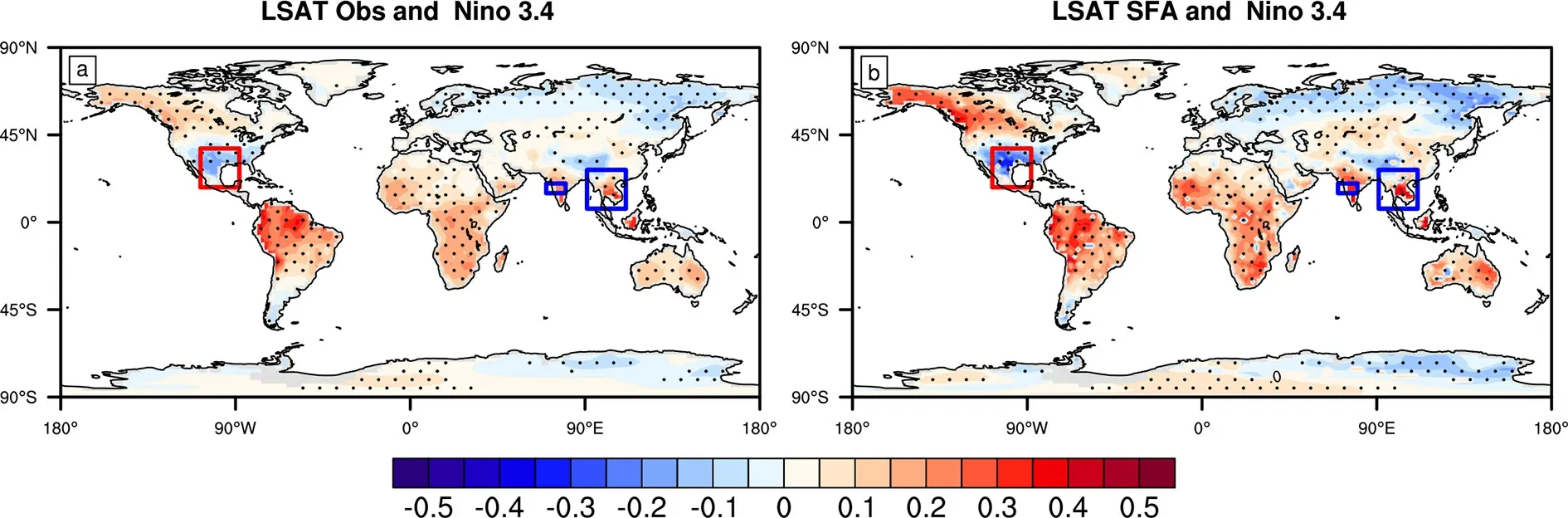
图5 同图1,但为1901~2009 年(a)观测LSAT、(b)SFA 方法提取的LSAT 慢变驱动力与逐月Niño3.4 指数的相关系数的空间分布。方框区域分别为北美洲南部(18°~38°N,88°~108°W)、印度地区(15°~20°N,70°~80°E)、中南半岛(7°~27°N,91°~111°E)Fig. 5 As in Fig. 1, but for correlation of (a) the original observed LSAT and (b) the LSAT slow driving force extracted by the SFA method with the monthly Niño3.4 index. The boxes represent southern North America (18°-38°N, 88°-108°W), India (15°-20°N, 70°-80°E), and the Indo-China Peninsula (7°-27°N, 91°-111°E)
当赤道东太平洋异常增暖(El Niño)时,北美洲南部和欧洲东北部LSAT 出现负异常。有研究表明太平洋地区存在PNA 大气遥相关模式,当北太平洋出现异常加深的阿留申低压时,西风增强且赤道太平洋中部降水增多,随着西风的增强,北美洲南部的温度则出现负异常(Yeh et al., 2018)。
在印度次大陆和东南亚地区,有学者提出海洋充电-放电的理论,El Niño 在冬季达到鼎盛时,印度洋在冬季后期和春季出现异常温暖的现象,从而加强亚洲夏季西南季风,导致印度和东南亚地区的陆地温度出现正异常(Timmermann et al., 2018)。基于此,有学者利用NAO 和ENSO 对东亚夏季风进行经验模型的预测(Wu et al., 2009)。
为了进一步研究ENSO 对局地LSAT 的影响,本文选取了三个地区,分别是北美洲南部(18°~38°N,88°~108°W)、印度地区(15°~20°N,70°~80°E)和中南半岛(7°~27°N,91°~111°E),以此来分析这些地区的LSAT 与Niño3.4 指数的相关性。
图6 说明三个地区与Niño3.4 指数特征非常相似,都有十分明显的年际变化特征,并且,SFA提取的LSAT 慢变驱动力信号依旧存在明显的年际变化特征,甚至在逐月时间尺度上,与Niño3.4 指数有很好的相关性。表3 显示,北美洲南部地区观测LSAT 与Niño3.4 指数的相关系数仅有-0.16,而SFA 提取的慢变驱动力信号与Niño3.4 指数的相关系数达到-0.32,相关系数的绝对值增加了将近一倍,解释方差增加了8%;印度次大陆的观测LSAT 与Niño3.4 指数也只有0.26,SFA 提取的慢变驱动力信号与其相关系数达到0.45,解释方差增长将近13%;同样,中南半岛地区的观测LSAT和驱动力与Niño3.4 指数的相关系数分别为0.19和0.32,解释方差增加了7%。以上结果表明,SFA 提取的慢变驱动力信号与Niño3.4 指数之间的相关系数的绝对值明显增大,解释方差也有大幅度的增长,进一步说明El Niño 在年际尺度上对这些地区LSAT 有很强的影响。
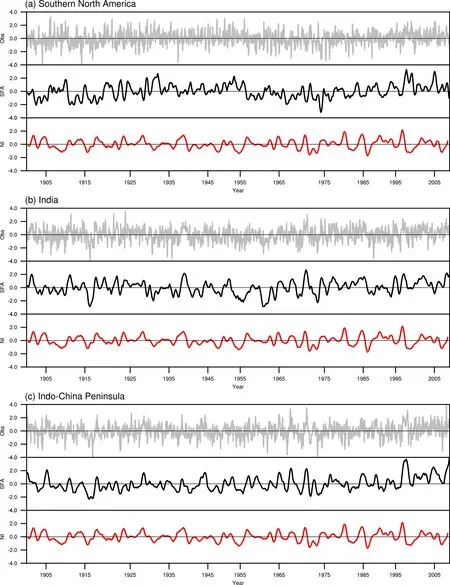
图6 同图2,但为(a)北美洲南部(18°~38°N,88°~108°W)、(b)印度地区(15°~20°N,70°~80°E)、(c)中南半岛(7°~27°N,91°~111°E)区域月平均LSAT 和逐月Niño3.4 指数。红线为逐月Nino3.4 指数经过12 个月滑动平均的标准化时间序列,灰线表示观测LSAT,黑线表示SFA 方法提取的LSAT 慢变驱动力Fig. 6 As in Fig. 2, but for the regional mean monthly LSAT in southern North America (18°-38°N, 88°-108°W), India (15°-20°N, 70°-80°E), and Indo-China Peninsula (7°-27°N, 91°-111°E) and the monthly Niño3.4 index (NI). The red lines run through the 12-month moving average The gray line represents the original observed LSAT. The black line represents the LSAT slow driving force extracted by the SFA method

表3 同表1,但为逐月Niño3.4 指数Table 3 As in Table 1, but for the monthly NI
Niño3.4 指数与观测LSAT 以及SFA 提取的慢变驱动力的相关系数对比结果表明,ENSO 事件影响LSAT 的主要区域范围为太平洋周边地区,包括北美洲、欧亚大陆,赤道低纬度地区以及南半球大部分地区,特别是北美洲北部和南部、南美洲中部、欧亚大陆东北部、非洲中南部、澳洲、南亚和中南半岛地区LSAT,与实际观测相比,可能受到ENSO 的更大影响。
3.4 PDO 对LSAT 的影响
有研究利用模式数据得出,PDO 作为太平洋海温模态之一,在外部辐射强迫的作用下,通过热量在海洋表层和深层的传递,对全球增暖加剧和停滞有重要影响(Meehl et al., 2013)。有研究表明PDO 由负位相变为正位相,欧亚大陆和北太平洋之间的海陆温度差异减弱,海陆风减弱,陆地温度出现负异常(Newman et al., 2016)。本节介绍了PDO 对全球LSAT 不同区域的影响。
有研究证明PDO 可以通过阿留申低压引起副热带太平洋地区和北美西部出现异常高压,在大气中引发北太平洋涛动现象(NPO, North Pacific Oscillation),还可以通过PNA 遥相关型影响北美气候。其也可以通过阿留申低压和西伯利亚高压影响东亚大气环流,进而影响我国气候的年代际变化(朱益民和杨修群, 2003; 杨修群等, 2004)。
以往研究表明,PDO 的空间格局与ENSO 相似,但二者在时间尺度上存在差异:ENSO 是年际尺度,PDO 是年代际尺度,大多数学者认为PDO可作为ENSO 的年代际背景,二者对不同地区LSAT 的影响存在较大的差异。图7 和图5 对比表明,即PDO、Niño3.4 两大气候指数与LSAT(以及驱动力)的相关系数的空间分布图显示,PDO与Niño3.4 指数的结果十分相似,相关性显著区域基本一致,但是PDO 的影响范围更广,强度更大。图7 表明,PDO 与北美洲北部、东亚部分区域(中南半岛)、印度次大陆、南美洲、非洲和澳洲地区的LSAT 呈现相同的相关关系,与欧洲东北部、北美洲南部地区的LSAT 有一致的影响。与Niño3.4 指数相比,PDO 对欧亚大陆北部地区、南美洲中部地区、北美洲、澳洲以及一些高纬度地区的LSAT 有更强的影响。其中的原因可能是高纬度地区的LSAT 在更大程度上受太平洋年代际海温模态的影响。为了进一步分析PDO 对局地LSAT 的影响,我们分别选取了北美洲西北部(50°~70°N,100°~160°W)、南美洲中部(10°~30°S,55°~65°W)、澳洲(20°~30°S,140°~150°E)和北美洲南部(25°~35°N,100°~105°W)四个地区来具体分析。
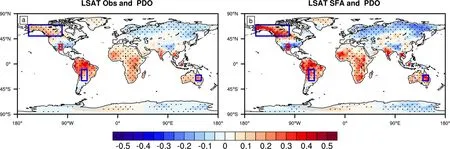
图7 同图1,但为1901~2009 年(a)观测LSAT、(b)SFA 方法提取的LSAT 慢变驱动力与逐月PDO 指数的相关系数的空间分布。方框区域分别为北美洲西北部(50°~70°N,100°~160°W)、南美洲中部(10°~30°S,55°~65°W)、澳洲东部(20°~30°S,140°~150°E)、北美洲南部(25°~35°N,100°~105°W)Fig. 7 As in Fig. 1, but for correlation of (a) the original observed LSAT and (b) the LSAT slow driving force extracted by the SFA method with the monthly PDO index. The boxes represent northwestern North America (50°-70°N, 100°-160°W), central South America (10°-30°S, 55°-65°W),Australia (20°-30°S, 140°-150°E), and southern North America (25°-35°N, 100°-105°W)
图8 显示,美洲、澳洲地区的LSAT 逐月观测时间序列存在着很明显的年际和年代际变化特征,而SFA 提取的LSAT 慢变信号表现出明显的年代际变化特征,且与PDO 年代际变化较为一致,如1910~1920 年前后均有“上升”—“下降”—“上升”的年代际变化特征。由此,可见PDO 对LSAT 的年代际变化有很大的影响。表4 显示,北美洲西北部地区的观测月LSAT 异常与PDO 的相关系数为0.18,SFA 提取的慢变驱动力信号却能达到0.35,增加了将近一倍,解释方差增加了9%。

表4 同表1,但为逐月PDO 指数Table 4 As in Table 1, but for the monthly PDOI

图8 同图2,但为(a)北美洲西北部(50°~70°N,100°~160°W)、(b)南美洲中部(10°~30°S,55°~65°W)、(c)澳洲(20°~30°S,140°~150°E)、(d)北美洲南部(25°~35°N,100°~105°W)区域月平均LSAT 和逐月PDO 指数。红线表示逐月PDO 指数,灰线表示观测LSAT,黑线表示SFA 方法提取的LSAT 慢变驱动力Fig. 8 As in Fig. 2, but for the regional mean monthly LSAT in (a) northwestern North America (50°-70°N, 100-160°W), (b) central South America(10°-30°S, 55°-65°W), (c) Australia (20°-30°S, 140°-150°E), and southern North America (25°-35°N, 100°-105°W) and the monthly PDO index(PDOI)The red lines represent the monthly PDOI. The gray line represents the original observed LSAT. The black line represents the LSAT slow driving force extracted by the SFA method
位于南半球的南美洲地区与澳洲地区,同样受到PDO 的影响。在表4 中,南美洲观测LSAT 与PDO 的相关性仅为0.16,SFA 提取的慢变驱动力信号与其的相关性达到0.32,相关系数绝对值增加了一倍,解释方差增加了8%;澳洲地区观测LSAT 与PDO 的相关系数为0.22,SFA 提取的慢变驱动力信号与其相关系数达到0.37,解释方差增加了9%。值得注意的是,北美洲南部地区受PDO 的影响也显著增强,观测LSAT 与PDO 的相关系数为-0.21,SFA 提取的慢变驱动力信号与PDO 的相关系数绝对值达到0.38,相关系数的绝对值显著增加,解释方差也增加了10%。因此,可以说PDO 对这四个地区LSAT 具有非常明显的影响,进一步证明PDO可能是太平洋周边尤其是高纬度地区LSAT 低频变率的重要驱动力之一。
PDO 作为北太平洋SST 的重要模态,对全球LSAT 有重要的影响。PDO 与ENSO 相比,对LSAT的影响范围更广,普遍扩展到热带外地区。本文研究结果说明受PDO 影响的区域不仅包括Niño3.4指数的显著区域,如太平洋周边陆地,如南北美洲、非洲、澳洲和欧亚大陆中南部,还包括北半球北部中高纬度地区,如欧亚大陆北部地区。且PDO 作为太平洋北部海温模态在更高纬度上影响LSAT 的低频变率。与此同时,PDO 在年代际尺度上对北太平洋和欧亚大陆的大气环流造成重要影响。
本文利用SFA 方法提取非平稳动力系统LSAT 的慢变驱动力,来探究LSAT 变化的内部机制。本章节将全球观测LSAT 与SFA 提取的慢变驱动力信号分别与GRF、AMO、Niño3.4 和PDO指数做相关分析,发现GRF 对全球LSAT 整体有显著影响,包括南极洲地区,相关性均非常显著。AMO 对北半球LSAT 中低纬度地区有重要影响,特别是北大西洋周边地区(北美洲东北部地区、格陵兰岛地区)和东亚地区LSAT 有显著一致的相关关系(Muller et al., 2013),并且在多年代际尺度上与LSAT 有密切的联系。Niño3.4 指数与大多数热带地区LSAT 显著相关,而PDO 指数结果与其相似,但是相关系数更大,范围更广,特别是在热带外地区,比如PDO 与北美洲北部、澳洲东部和欧亚大陆北部等中高纬度地区有显著的相关关系。选区结果表明,与观测LSAT 时间序列相比,SFA 方法提取的慢变驱动力与四个指数的相关系数绝对值明显增大,解释方差也明显增加。以上结果说明LSAT 确实受GRF、AMO、Niño3.4、PDO气候指数的显著影响。而且,从解释方差来看,三大SST 模态与观测LSAT 的解释方差并不高,而且均不超过10%,而SFA 方法提取的慢变驱动力与三大SST 模态的解释方差均超过10%,有的甚至达到20%(Niño3.4 指数与印度地区平均LSAT慢变驱动力的解释方差)。
4 模式验证
为了验证三大SST 模态是LSAT 低频变率的重要驱动力,我们利用CAM5 模式设计的AMIP试验进行分析。AMIP 试验是基于海表温度作为下垫面条件来驱动的大气环流模式,因此可以反映海温对大气环流和陆地气温的强迫作用。本文综合模式中10 个集合的平均结果,减少了大气内部过程对LSAT 的影响,保留了辐射和海温等对LSAT 的影响。通过分析AMIP 试验模拟出的LSAT 与AMO、Niño3.4、PDO 指数的相关分析结果,进一步说明三个SST 模态对LSAT 低频变率有重要作用。以往有研究通过观测的海面温度(不包括人为变暖)强迫进行大气模型模拟试验,证明观测到的海上风应力异常,即太平洋信风的减弱/增强,与全球表面增温/降温有很好的一致性,进而证明年代际自然气候变率对实际观测到的全球平均表面温度有重要贡献(Nakaegawa et al., 2004; Watanabe et al., 2014)。
已有研究结果表明,GRF 与LSAT 的相关性在全球范围内非常显著(Forest et al., 2006; Hansen et al., 2011; 张华和黄建平, 2014; Marvel et al.,2016),并且在模式结果中整体呈现显著正相关特征,所以在本节中不做介绍。
本节利用模式模拟出的LSAT 分别与AMO、Niño3.4、PDO 气候指数分别做空间相关分析,得出LSAT 与AMO、Niño3.4 和PDO 三个气候指数同期相关系数的空间分布图。结果表明,AMO、El Niño 和PDO 分别对LSAT 有重要的影响。
4.1 AMO 对LSAT 的影响
图9 显示,全球范围内大部分地区LSAT 与AMO 有很强的相关性,在大西洋周边地区(北美洲东部、格陵兰岛、南美洲)(Weaver et al., 2009;Merrifield and Xie, 2016)、阿拉伯海周边地区、欧亚大陆大部分地区、非洲北部和南部地区都呈现显著的正相关关系。与实际观测结果相同,AMO 对北半球的陆地温度有较大影响,尤其是大西洋周边以及中低纬度地区。而AMO 对东亚部分地区的影响与实际观测结果有一定偏差。据相关系数的分布图显示,亚洲的高值区距离选定的东亚地区偏东一点。而且,AMO 对非洲部分北部和南部地区有明显显著的影响,例如非洲北部、大西洋沿岸和非洲东南部地区,而非洲中部地区没有明显影响。在南极洲,模拟结果与观测结果一致,但是与SFA 提取的慢变驱动力的结果相差较大。总的来说,模拟与观测结果一致,AMO 对大西洋周边地区和亚洲大部分地区LSAT 有非常重要的影响。
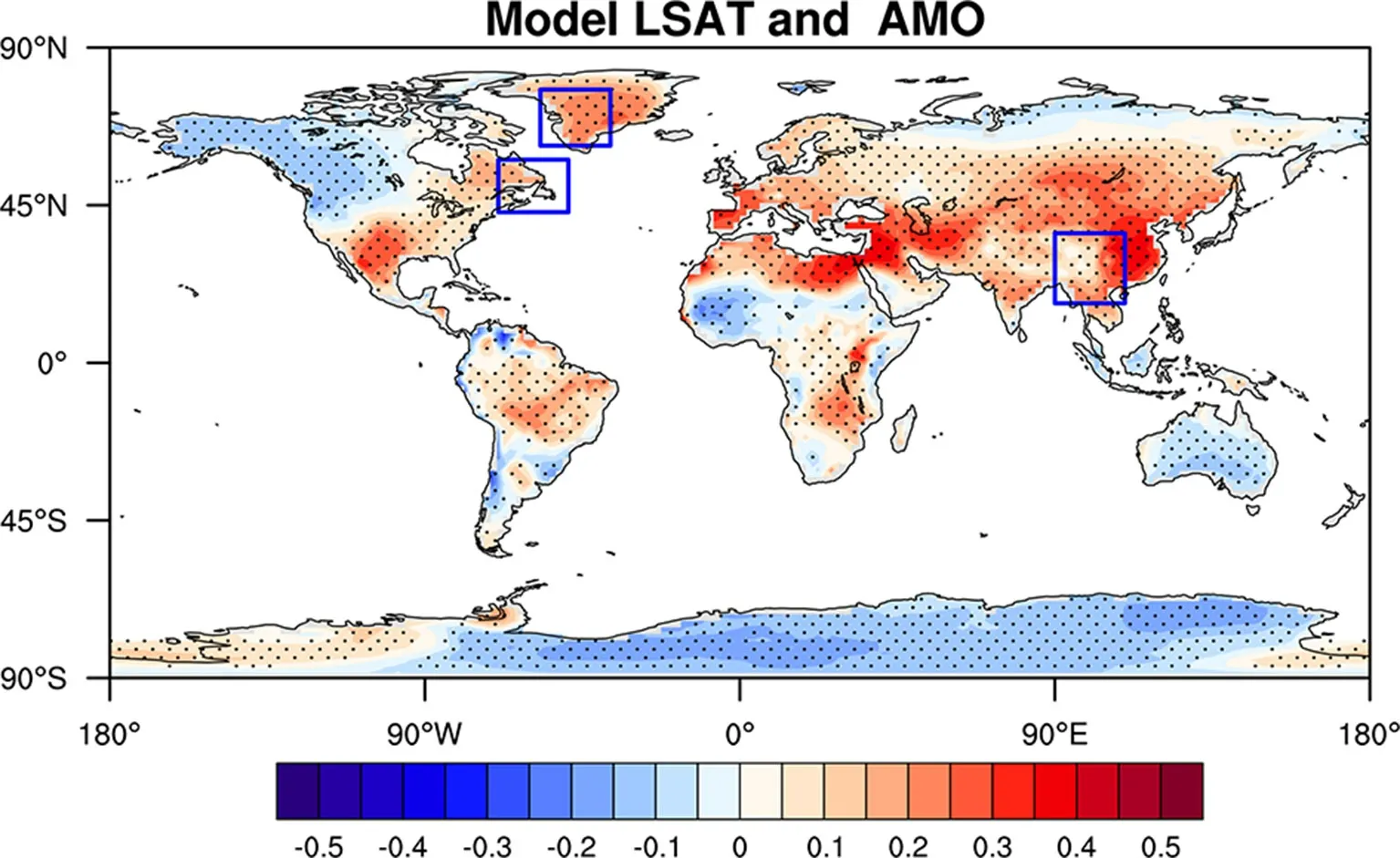
图9 AMIP 试验10 个集合平均1901~2009 年的LSAT 与逐月AMO 指数同期相关系数的空间分布。方框内为据观测结果选择的关键区,黑色打点区域代表通过95%的信度水平检验Fig. 9 Correlation of the ten sets averaging LSAT simulated by the AMIP experience with the monthly AMO index for the same period from1901-2009. The boxes represent the key areas selected according to the observation results, regions above 95% confidence level are black spotted
4.2 El Niño 对LSAT 的影响
图10 模式结果显示,全球LSAT 受到ENSO的显著影响,特别是太平洋周边和赤道低纬度地区,包括南半球陆地整体受到其显著影响。在北美洲西北部、南美洲、格陵兰岛、非洲、澳洲和东亚等地区,LSAT 受到Niño3.4 指数显著一致的影响;在北美洲南部、欧亚大陆北部以及南美洲南部地区有明显一致的相关关系。此前也有模式模拟结果表明热带太平洋海温可以强迫出北美冬季(1982 年12月至1983 年3 月)平均地表温度异常(Hoerling and Kumar, 1997; 容新尧和杨修群, 2004, 2005),东亚季风受到ENSO 的显著影响(Ju and Slingo,1995),本文结果与其基本一致。
模式结果与观测结果对比表明,Niño3.4 指数与北美洲南部、印度南部和东亚地区的LSAT 的相关性非常显著。但在印度中北部,模式模拟试验未能模拟出与实际观测相同的结果。这可能是因为模式选用的AMIP 观测海洋模式,没有增加气候系统中海洋—大气反馈,而太平洋与印度洋之间这种反馈非常复杂,所以未模拟出想要的结果。总而言之,Niño3.4 指数对太平洋周边和赤道低纬度地区LSAT的影响较大。
4.3 PDO 对LSAT 的影响
模式模拟结果与实际观测结果一致的是,PDO 与Niño3.4 指 数 的 结 果 相 似。图11 表 明,PDO 在北美洲西北部、南美洲、非洲、澳洲、东亚部分地区(中南半岛)、以及印度次大陆南部等区域呈现一致且显著较强相关,在北美洲南部、欧洲东北部和南美洲南部等部分区域呈现一致显著相关。值得注意的是,PDO 指数与北美洲西北部和南部、南美洲中部和澳洲东北部四个地区的LSAT的相关系数绝对值能够达到0.5。图10 和图11 表明,与Niño3.4 指数的模式模拟结果相比,PDO 指数对欧洲东北部的影响更大,而对格陵兰岛地区LSAT 的影响较小。此外,以往模式结果表明PDO 对澳洲西海岸海水表面异常增温有重要的影响(Tanuma and Tozuka, 2020)。
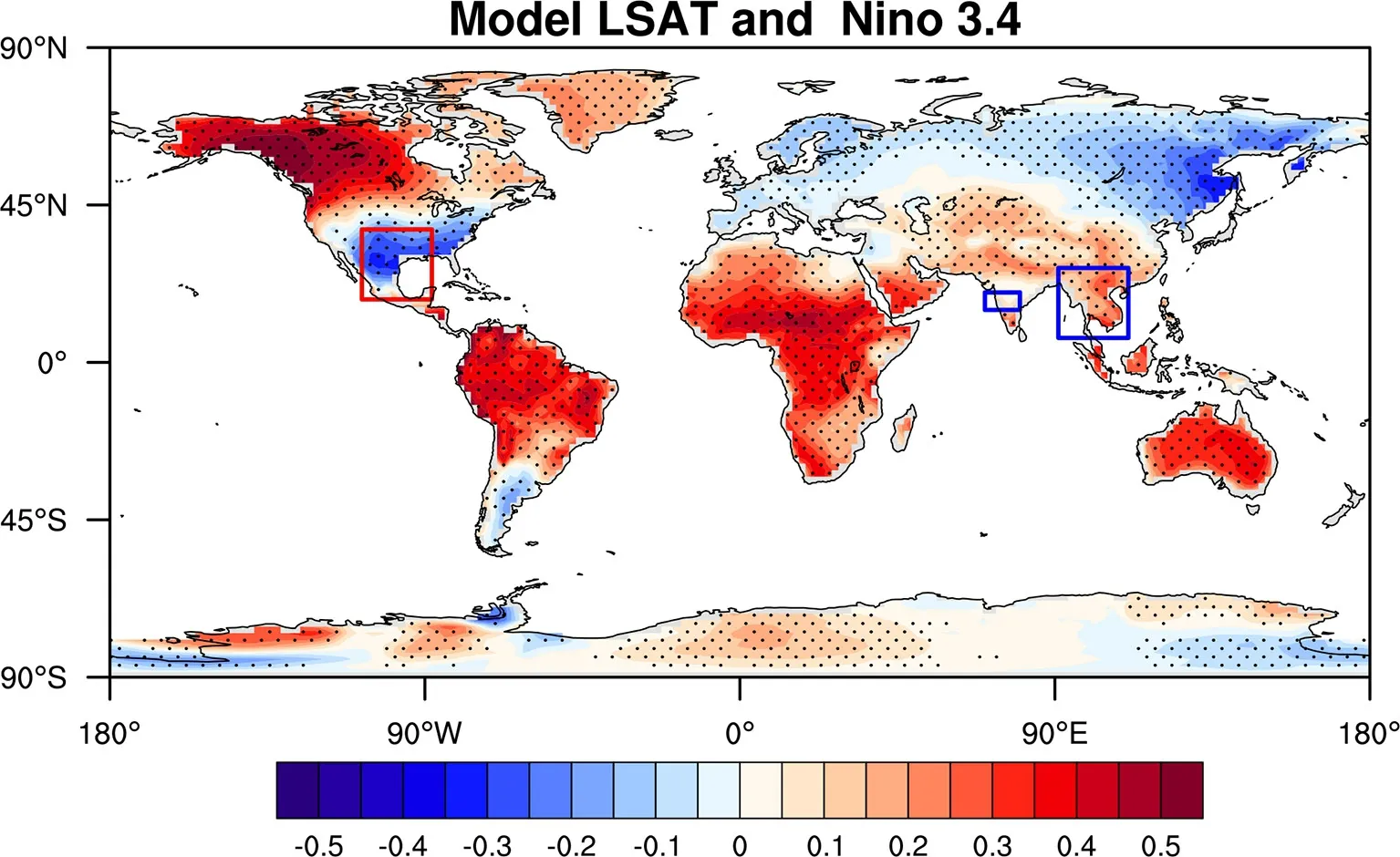
图10 同图9,但为AMIP 试验10 个集合平均1901~2009 年的LSAT 与逐月Niño3.4 指数同期相关系数的空间分布Fig. 10 As in Fig. 9, but for correlation of the ten sets averaging LSAT simulated by the AMIP experience with the monthly Niño3.4 index for the same period from 1901~2009
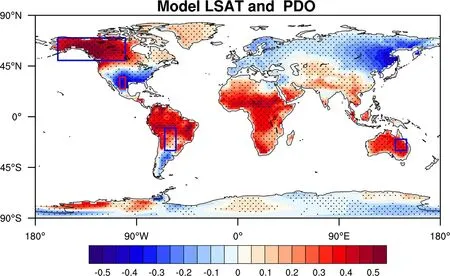
图11 同图9, 但为AMIP 试验10 个集合平均1901~2009 年的LSAT 与逐月PDO 指数同期相关系数的空间分布Fig. 11 As in Fig. 9, but for correlation of the ten sets averaging LSAT simulated by the AMIP experience with the monthly PDO index for the same period from 1901~2009
通过以上三个模式结果,可以得出一致结论:AMO 对北半球中低纬度地区,尤其是大西洋周边地区(北美洲东南部和格陵兰岛)、欧亚大陆南部地区(特别是东亚地区)LSAT 有显著影响;El Niño 和PDO 对太平洋周边地区(北美洲和南美洲、澳洲、欧亚大陆北部和南部)和赤道低纬度以及南半球LSAT 有重要的影响。其二者均与北美洲西北部、南美洲中北部、非洲、东亚部分地区和澳洲地区的LSAT 有一致显著相关关系,与北美洲南部、欧亚大陆北部有一致显著的相关关系。二者比较而言,El Niño 对低纬度地区有较大的影响,而PDO对更高纬度地区(如欧亚大陆东北部)有较大的影响。而且,PDO 的影响强度更大,范围更广,可扩展热带外地区。AMIP 模式试验的结果也进一步验证了此前SFA 提取的LSAT 慢变驱动力与海温主导模态(AMO、El Niño 和PDO)之间的密切联系,并且提供了模式证据来说明海温主导模态是LSAT 低频变率的重要驱动力。
5 总结与讨论
近年来,SFA 方法被应用于气候变化研究领域,用于探究气候变化的潜在驱动力及相关的动力学机制。以往研究多聚焦某个区域平均气候要素的慢变驱动力分析,而一维时间序列在分析包含时—空协同演变信息的多维数据方面有局限性。全球范围内,不同地区气候要素慢变驱动力之间的关系以及慢变驱动力的空间结构特征尚不清楚。本文以LSAT 为例,将SFA 方法拓展到多维时空的LSAT场中研究其低频变率特征及驱动力,并且与气候系统外部辐射强迫(GRF)和主要的气候系统内部变率(AMO、Niño3.4 和PDO)进行对比分析,揭示了LSAT 慢变驱动力与外部强迫和内部变率因子之间的紧密联系,以及LSAT 对这些驱动因子响应的空间特征。结合数值模式结果验证了内部变率是区域LSAT 低频变化的重要驱动力。结论具体如下:
(1)GRF 对LSAT 变率的影响有全球一致性的特征。AMO 对北半球LSAT 变率有很大影响,特别是中低纬度地区。在大西洋周边、格陵兰岛和南亚地区,LSAT 变率与AMO 指数有一致显著的相关关系。Niño3.4 指数与PDO 指数的显著性区域有很大的相似性,在北美洲西北部、南美洲大部分地区、非洲、澳洲和亚洲南部,包括印度次大陆有一致显著的相关关系,在北美洲南部、欧亚大陆北部和东部有一致显著的相关关系。不同的是,PDO作为北太平洋海温模态,其影响范围和强度明显增强,可扩展到热带外地区。
(2)SFA 方法提取出的LSAT 驱动力作为气候系统的慢变驱动力信号的组合,能够有效地降低时间序列中噪声信号的干扰。与实际观测相比,GRF 和三大SST 模态与SFA 提取LSAT 的慢变驱动力之间的相关系数绝对值明显增大,对LSAT 低频变率的解释方差显著增大。特别是AMO、Niño3.4、PDO 这三大SST 模态的解释方差明显增大,基本都在2 倍以上。
(3)模式结果进一步验证了三个海温模态对LSAT 变率的重要影响。AMO 对大西洋周边地区(北美洲东北部、格陵兰岛)和南亚地区有很强的影响;El Niño 和PDO 存在相似特征,与北美洲西北部、南美洲、非洲、澳洲和亚洲南部LSAT 有一致的强相关关系,而对北美洲南部、欧亚大陆北部和东部LSAT 存在一致的强相关关系。与观测不同的是,模拟结果中,印度次大陆LSAT 与Niño3.4、PDO 显著相关的区域范围较小,可能受到真实地形和季风的影响。
本文分析了GLSAT 受到GRF 和三个海温模态(AMO、El Niño、PDO)的影响。在自然界实际存在一些其他的海温模态,如北太平洋环流振荡 NPGO (North Pacific Gyre Oscillation)( Di Lorenzo et al., 2010)、中部型ENSO(何珊珊等,2015)等。过去一些研究中关于海温时空模态分析中解释方差较小的海温模态,如NAO 以及IOD 等对区域海陆气相互作用存在一定的影响(Messié and Chavez, 2011),对这些模态在区域以及全球气候变化方面的影响可能需要进一步研究。
此外,各种海温模态之间可能存在相互影响,比如协同、拮抗作用(Li et al., 2019)等,所以各个模态相对于气候系统的共同作用以及相互响应有待进一步深入研究。
最后,全球气候系统包括多种要素的共同作用,温度是地球表层系统最重要的一个要素之一,要想揭示全球气候系统的驱动力,可能还需要结合降水等要素,对气候系统进行全面的分析与研究。

