电力系统暂态功角失稳与暂态电压失稳的主导性识别

李凯恩，石定中，张 磊，杨明贵，刘 勇

（云南电网有限责任公司临沧供电局，云南临沧 677000）

0 引言

电力系统故障后暂态过程体现为暂态功角失稳和电压失稳，一旦出现电力系统失稳，比如功角失稳会从一定程度上导致电压崩溃，而电压崩溃会引发功角失稳。通常暂态功角失稳和电压失稳往往相互交织，仅通过电压和功角无法准确分辨系统故障之后的失稳模式。目前研究学者提出多种功角电压失稳的实用判据和理论判断。为此本研究从大型变电站变电断面有功功率的特点着手，详细阐述了暂态功角失稳和电压失稳模式提出主导系统变量，并进一步提出识别系统主导失稳模式的方法，通过仿真分析证明该方法的有效性。

1 电力系统失稳后主导系统变量

1.1 变电断面有功功率

对于一些大型电力系统来说可根据系统任意变电断面潮流方向，将该系统作为简单受送端模型。在其模型中送端系统为A 区域具有发电性质，受端系统为B 区域，具有负荷性质，结合送受端系统的特点能够将其等值为单机单负荷。

上述公式忽略电力暂态中线路参数的变化，可将电力暂态中变电断面电磁功率利用全微分公式进行表示。

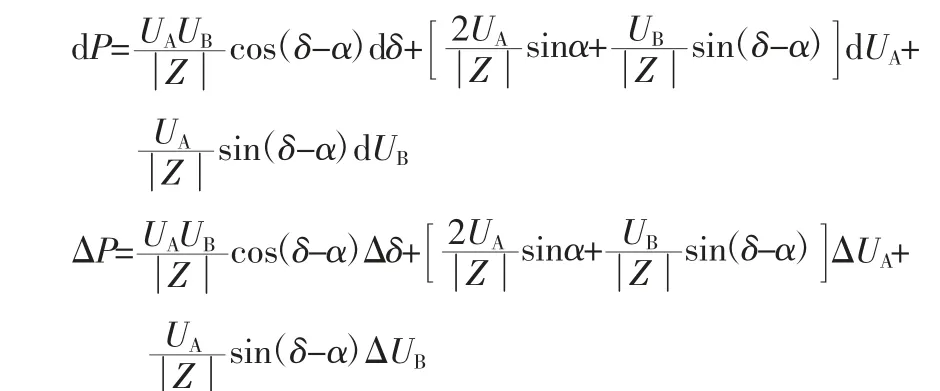
根据上述公式，两端母线电压变化量以及电压相角差变化量即变电断面功率的变化。

1.2 选取主导系统变量值

电力系统可根据失稳后主导系统变量来区分功角或电压稳定问题，选择合适主导系统变量是十分重要的。本质上，电力系统是能量传输系统，是由变电站、电源、负荷和电网构成的，一般主要分析电源侧功角问题以及负荷测电压问题。根据方程可知，功角从本质上是由于不平衡功率导致的，与线路遥控功率有一定联系，而电压稳定主要与系统向负荷供电能力有关，本质上属于线路有功功率问题。可将上述公式进行转换为：

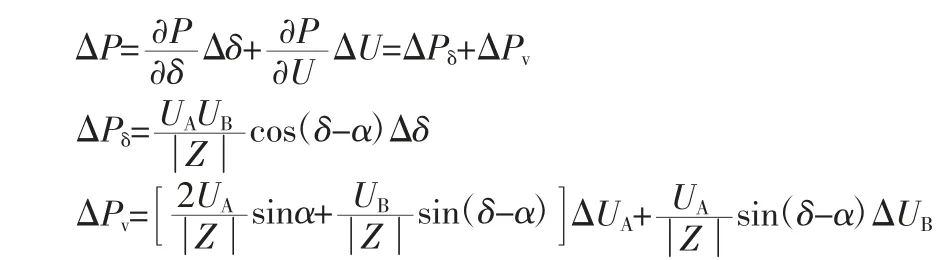
在该公式中，电力系统暂态中变电断面有功功率变化量分为：第一与母线电压相较有关，能够作为母线电压相角差变化量；第二与母线电压变化程度相关，可作为母线电压负值变化量。在扰动之后，电力系统暂态中两个变量能够从一定程度上决定系统之间变电断面功率变化，进而影响整个电力系统稳定性，因此可将上述两个变量作为主导系统变量，进一步分析电力系统电压和功角稳定相关问题，并阐述该变量电力系统失稳模式之间的关系。

2 分析电力系统的失稳模式

电压和功角失稳可以用ΔPδ、ΔPv表示：当电力系统运行点超过该曲线不平衡点时电力系统会进入功角失稳模式，而当电力系统运行点越过曲线中PMax点，这种情况下电力系统会进入电压失稳模式。

2.1 电压失稳模式

一般来说，在电力系统失稳过程中电压和功角失稳会同时发生，这种情况下电力系统运行点会位于电压和功脚失稳区间范围内。根据曲线可以发现，变电站的配电电磁功率会随着功角差增加而逐渐降低，负荷功率会随电压降低而逐渐降低，对于受送端的电力系统来说，送端系统A 所发出的电磁功率可用功率Pe表示，受端系统B 实际电磁功率可用P1表示，如果忽略电磁损耗，此时电磁功率与受端系统功率是相等的。当主导失稳为电压失稳状态时此时根据电压稳定性概念，系统对负荷供电能力无法满足实际负荷需求，也就是负荷实际电磁功率低于负荷所需要的功率，则有：

2.2 功角失稳模式

当电力系统处于失稳状态时并且电压和功角同时是处于失稳模式，根据曲线可以发现，发电机输出电磁功率随功角差的变化以及负荷实际功率随电压的变化规律仍然成立。当主导失稳状态表现为功角失稳模式时，根据功角稳定性可以发现，在发电机的转子中存在不平衡转距，进一步可以发现当受送端电力系统处于失稳状态，此时受送端A 等值变电站变电功率应当高于系统A 所配电输出电磁功率，如果忽略电磁损耗，此时电磁功率与受端系统获得的功率是相等的。预测未来电力系统会出现功角失稳，且目前未出现失稳，则上述公式不成立，但采用预测的方式则上述公式是成立的，因此仅需确定电力系统出现功角失稳作为主导失稳则上述公式成立。

一般电力系统失稳为单一失稳，也就是系统出现纯电压失稳或纯功角失稳，这种情况下典型电压失稳可以利用无穷大母线接入单负荷进行表示。当处于纯电压失稳时，电压相位角变化可以忽略，进而Δδ 接近0，则：

同时，对于功角失稳来说，可以利用单机无穷大母线系统来表示，并且在纯功角失稳时可忽略母线电压负值变化量，进而ΔV=0，则：

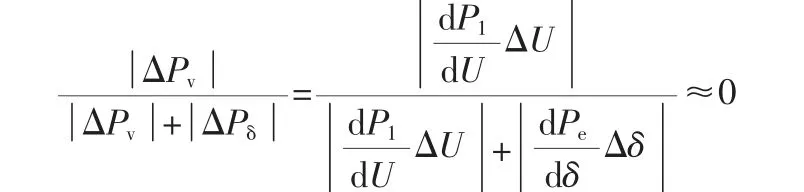
根据上述公式可以发现，本质上纯电压失稳模式与电压失稳为主导失稳具有相同特点。同理，纯功角失稳与功角失稳为主导的失稳模式同样具备相同特征，因此可以将纯电压失稳和纯功角失稳可作为主导失稳的两种极端进行分析。

3 功率全微分的失稳模式识别

结合上述分析，同感变电断面有功功率全微分方程可获得变电断面有功功率变化量包含两个函数值。根据处于不同失稳状态下具备不同特点来看，当主导失稳模式为电压失稳模式，这种情况母线电压幅值会影响变电断面功率改变量而出现纯电压失稳，此时全部由母线电压负值分量来决定；对于功角失稳这种情况，变电断面功率改变量主要是与部分母线电压相角差分量有关，在处于纯功角失稳下则全部由母线电压相角差分量决定，进而可获得主导失稳模式的识别指标S，其中。

以S 作为主导失稳模式的识别指标，可以利用变电断面功率改变量以及分量曲线几何距离进行表示，当主导模式为功能失稳，这种情况下量曲线距离较小具有较高的重合度，在极端条件下两个曲线会重合，这种情况下也使ΔPδ是导致变电断面功率改变量发生变化的主要因素。因此，对于基于主导失稳模式识别指标，在进行电力系统失稳模式主导识别过程中：当负荷S 介于0～1/2 时，此时主导失稳模式为功角失稳；当S 介于1/2～1时，此时主导失稳模式为电压失稳；当S 等于1/2 时，两分量相等，处于临界值无法准确识别系统的主导失稳模式，需要进一步分析。在这一过程中主导性识别指标并不是系统稳定判断的能力，需要结合失稳数据进行判断，当系统失去稳定时需要利用主导性识别指标进而确定主导性失稳模式，能够为后续采取紧急措施提供依据。

4 仿真分析

（1）本研究提出利用功率全微分失稳模式主导性识别法。针对该方法实现仿真分析，利用电力系统全过程动态仿真程序中扰动响应数据，进一步模拟电力系统实时测量数据，以证明该方法的有效性，并使用3 机10 节电等值系统。该系统的负荷模型为：100%恒阻抗负荷为B7，电动机负荷为B10，在0 s B6位置出现三相短路故障，在经过0.005 6 s 之后该故障切除。根据稳定曲线可以发现，目前该系统出现电压失稳模式，根据电压曲线进一步发现受端区域的电压持续降低，计算主导失稳模式识别指标，可以发现主导失稳模式识别指标均大于0.5，证明此时电压失稳为系统的主导失稳模式，需要采取切负荷紧急控制措施，在2.58 s 时切除B10 位置的负荷，且根据电压和功角曲线可以发现，通过切负荷措施之后能使电力系统恢复正常运行。

（2）使用IEEE9 节电系统。在该系统中各负荷均为恒阻抗，在0 s 时线路bus5～7 出现电路故障。结合曲线可以发现，此时电压和功角失稳同时存在，如果单从电压、功角的形式上很难准确判断目前系统主导失稳模式，因此无法采取有效紧急控制措施，进一步计算主导失稳模式识别指标S，结果发现S 均低于0.5，证明此时系统功角失稳是其主导失稳模式，需采取切机措施。0.3 s 时在B2 位置进行发电机切机，为经采取措施之后根据电压和工作曲线可以发现，采取前期措施是有效的，能够使电力系统恢复稳定运行。

5 结束语

对于电力系统变电站出现故障采取紧急措施时，准确区分暂态功角和电压失稳是其前提。在基于变电系统断面有关功率特点分析的前提下，能够利用功率全微分方程提出主导系统变量，该变量能够用于反映系统失稳模式。结合现有失稳判据，利用提出的系统失稳识别模式能为后续暂态稳定措施提供重要依据。