Analysis and Strategy Research on the Mathematics Learning Situation of the Postgraduate Candidates

Hanyutang WANG, Yumo ZHOU, Bo ZHEN, Min HUANG, Falei YANG, Yongjia MA, Hong FANG, Liyan XU

College of Basic Sciences, Tianjin Agricultural University, Tianjin 300384, China

Abstract This study takes the students who intend to study for graduate students as the research object, and makes a questionnaire survey on the mathematics learning situation and learning platform of the postgraduate candidates.Questionnaires were distributed online and offline, and a total of 326 valid questionnaires were collected.Based on 326 questionnaires, this paper analyzes the current learning situation of mathematics in the postgraduate entrance examination and studies the strategies based on the present situation, which points out the direction for the construction of mathematics learning and communication platform based on the needs of postgraduate entrance examination.

Key words Postgraduate candidates, Mathematics for the postgraduate entrance examination, Learning Situation, Present situation analysis, Strategy research

1 Introduction

In the past five years, the number of applicants for the national postgraduate entrance examination has increased rapidly.In 2017, the number of postgraduate applicants broke through the 2 million mark for the first time, reaching 2.01 million; in 2021, the number of postgraduate applicants reached 3.77 million.In the past five years, the number of applicants for the postgraduate entrance examination has nearly doubled.

With the growth of the number of applicants for the postgraduate entrance examination year by year, tutoring classes for postgraduate entrance examination, online courses and question search apps have emerged one after another.In view of the mathematics for the postgraduate entrance examination, we have carried out an investigation and research on the problems and real needs encountered by the postgraduate candidates in learning mathematics for the postgraduate entrance examination.

2 Data sources

This study takes the students who are interested in studying for graduate students as the research object, designs a questionnaire according to the mathematics learning situation of the postgraduate candidates and the use of the platform, sends out the questionnaire through online and offline channels, and collects a total of 326 valid questionnaires.

3 Questionnaire survey and data processing

3.1 Survey and data analysis of the basic situation of the applicants for postgraduate entrance examination

3.1.1Object of survey.The number of valid subjects in this questionnaire is 326, of which 93% are undergraduate students and 7% are junior college and undergraduate graduates.51% are boys and 49% are girls, with a male-to-female ratio approaching 1∶1.

3.1.2Willingness to take the postgraduate entrance examination.The statistical results of the questionnaire data are shown in Fig.1.About 58.89% are interested in taking the postgraduate entrance examination, 24.53% are under consideration, and 16.56% are not interested in taking the postgraduate entrance examination.The number of people who have a clear intention to take the postgraduate entrance examination accounts for nearly 60%, which has been more than half, thus it can be seen that the proportion of people who choose to take the postgraduate entrance examination is very high, and the postgraduate entrance examination has been considered by most people.

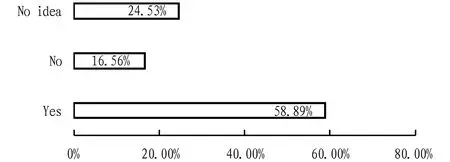
Fig.1 Statistics of willingness to take the postgraduate entrance examination

3.2 Survey and analysis of the real mathematical problems in the postgraduate entrance examination

3.2.1Mathematics for postgraduate entrance examination.Referring to the data, it is known that nearly half of the majors in the postgraduate entrance examination need to take the math test in the postgraduate entrance examination.According to the data of the questionnaire survey, among the 326 respondents, 167 will take part in the postgraduate entrance examination on mathematics, accounting for 51.23%.

3.2.2Mathematical types in postgraduate entrance examination.There are three types of mathematics papers for the postgraduate entrance examination, which are Mathematics 1, Mathematics 2 and Mathematics 3.Mathematics 1 covers the widest range of knowledge points, and it is suitable for science and engineering majors.56.44% of the respondents take Mathematics 1.Mathematics 2 requires the least knowledge, with Probability Theory and Mathematical Statistics not involved, 23.93% of the respondents take Mathematics 2.Mathematics 3 is suitable for economics majors, with 19.63% of respondents taking Mathematics 3.

3.2.3Years for mathematics in postgraduate entrance examination.The survey data of the years required for the mathematics in postgraduate entrance examination show that 64.11% and 18.40% of the students think that they need to review the real math questions within 5 and 6-10 years, respectively, so 82.51% of the respondents think that they need the postgraduate entrance examination questions within 10 years.

3.2.4Mathematical question ranking in the postgraduate entrance examination.According to the questionnaire survey data, this paper makes a cross-analysis of the presentation of the expected mathematics real questions for the postgraduate entrance examination, and the results are shown in Table 1.Table 1 shows that 63.5% of the respondents expected real questions to be presented by year, 57.1% expected real questions to be presented according to mathematical types, 55.2% expected real questions to be presented according to knowledge points, and 40.5% expected real questions to be presented according to math curriculum.

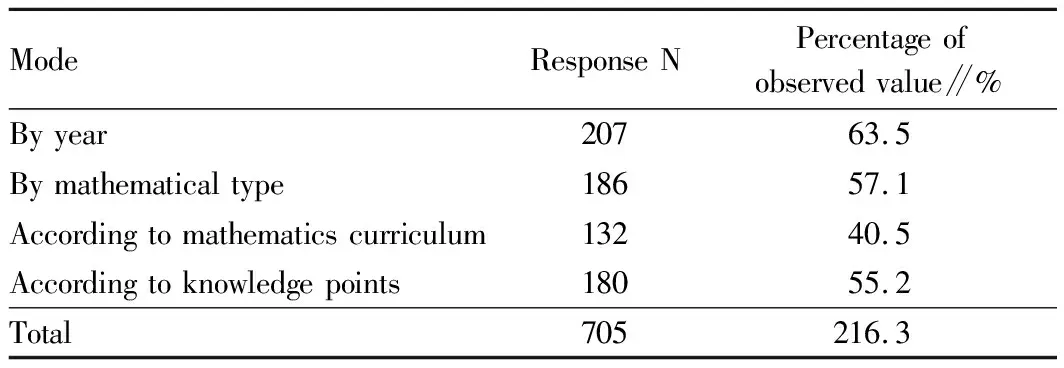
Table 1 Cross-analysis of the presentation of mathematical real questions for the postgraduate entrance examination

Table 2 Cross-analysis of the expected score of mathematics for postgraduate entrance examination and foundation of mathematics

3.3 Conditions of the candidates for the postgraduate entrance examination

3.3.1Foundation and expected score.Based on the survey data, the expectation of mathematical scores at the present stage and their own mathematical foundation are cross-analyzed, and the results are shown in Table 2.Table 2 shows that students with expected scores of 90-110 are the most, with 116 students, while those with expected scores of 130-150 are the least, with 35 students.65% of the students with expected scores of 90-110 have "average foundation".The expected score of students with a good foundation is generally more than 110; the expected score of students with a solid foundation is mostly between 90 and 130.

3.3.2Mastery of the types of questions.From the analysis of the type of questions in examination paper, the mathematics of postgraduate entrance examination includes multiple choice questions, gap filling questions and solution questions, there are eight multiple choice questions, six gap filling questions and nine solution questions, and the score of solution questions is relatively high.The statistics of the survey data are shown in Fig.2.

It can be seen from Fig.2 that students generally lack a good grasp of solution questions, especially more than 70% of students lack mastery of proof questions and comprehensive questions(74.78% and 71.30%, respectively).

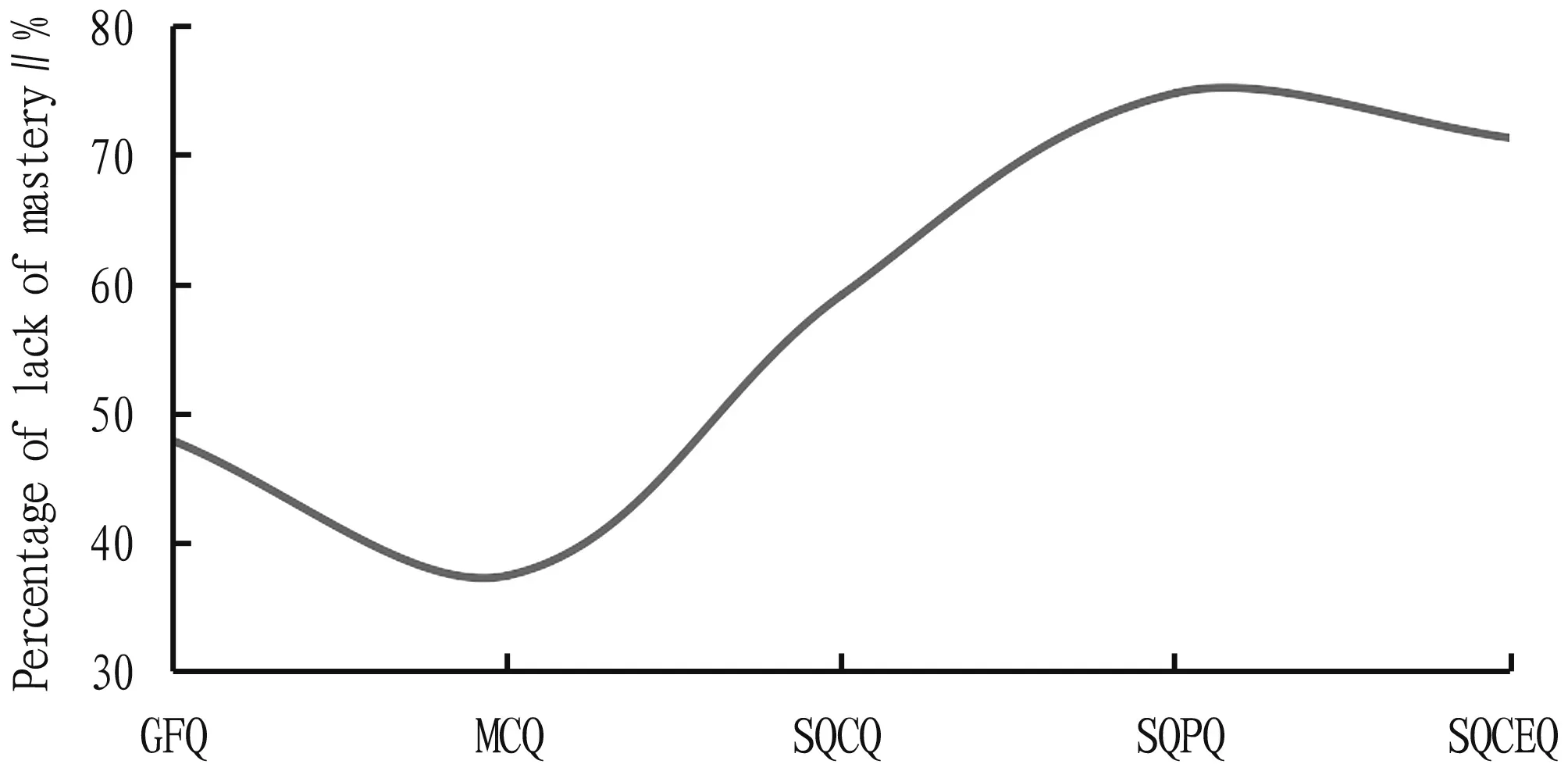
Note: GFQ—Gap filling questions; MCQ—Multiple choice questions; SQCQ—Solution questions-computing questions; SQPQ—Solution questions-proof questions; SQCEQ—Solution questions-comprehensive questions.

3.4 Mathematics preparation for the postgraduate candidates

3.4.1The preparation method of mathematics for postgraduate entrance examination.The survey data of the postgraduate candidates’ method of preparing for the postgraduate entrance examination is shown in Fig.3.About 52% of the students are self-taught with online courses and books, 21% are self-taught through online courses, 18% are self-taught with the help of books, and 9% participate in tutoring organizations.The data show that more than 70% of the students prepare for the postgraduate entrance examination with the help of online courses, which shows that learning software is widely used in the preparation for the postgraduate entrance examination.

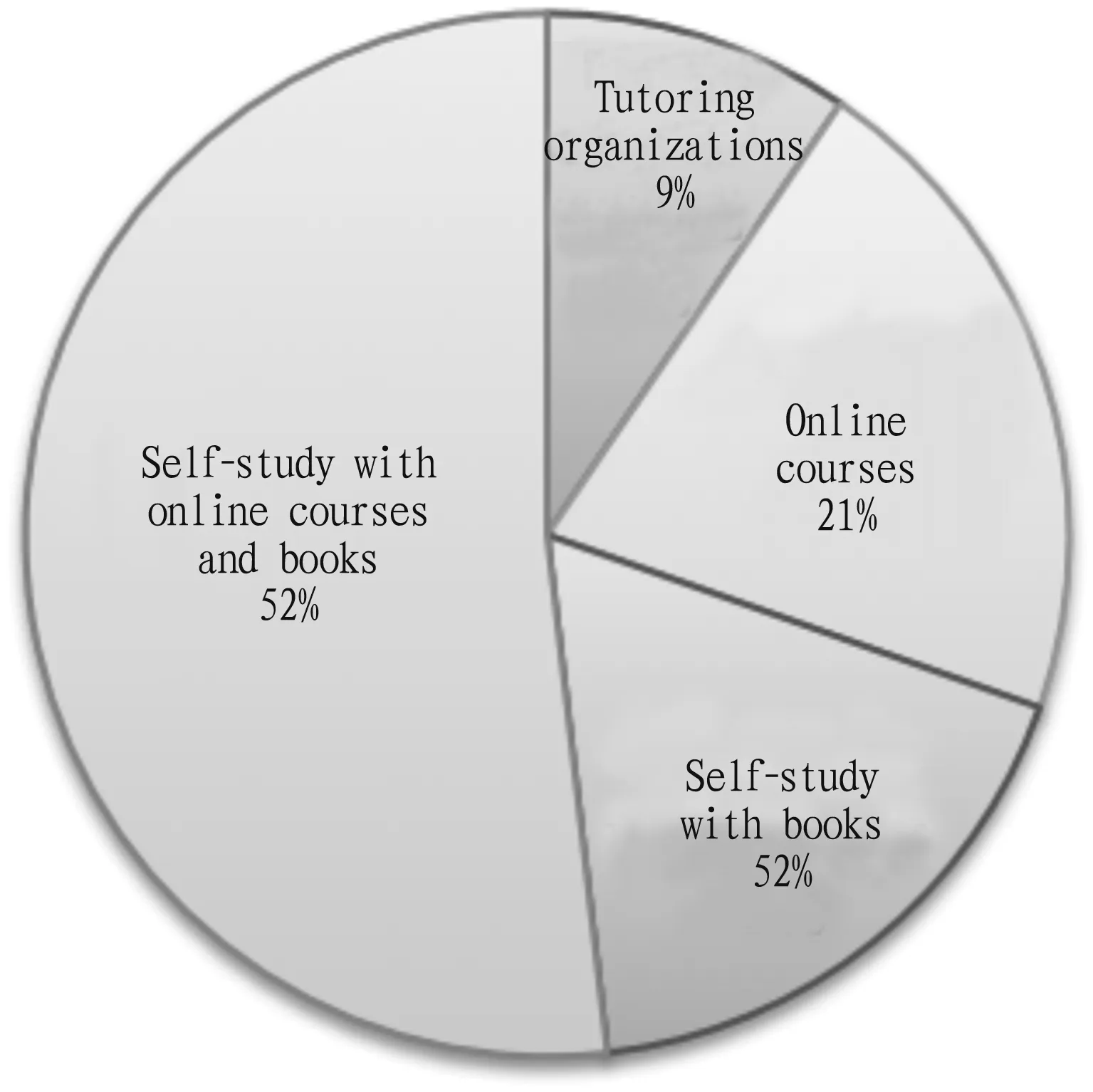
Fig.3 Mathematics learning methods for postgraduate entrance examination

3.4.2Selection of network tools.With the rate of postgraduate entrance examination increasing year by year, the demand for postgraduate entrance examination is becoming more and more urgent, and learning software platforms with their own characteristics emerge endlessly.The survey data are shown in Fig.4: 36% of the students use Baidusouti, 32% use Xiaoyuansouti, and 23% use Zuoyebang.

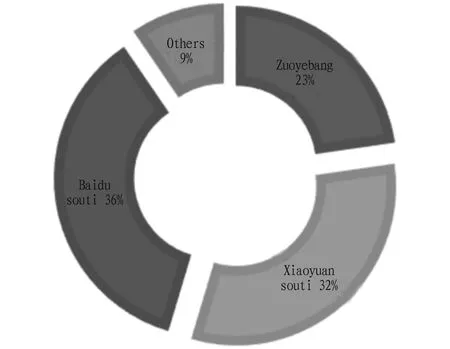
Fig.4 Selection of network tools for mathematics learning for postgraduate entrance examination

3.4.3Evaluation of learning software.Learning software can solve the problems encountered by the postgraduate candidates in preparing for the postgraduate entrance examination and provide targeted guidance, but there are deficiencies in the use of the software.The survey data are shown in Fig.5, and the results show that the number of people who think that "real questions are not classified, few teachers explain them, it cannot answer questions in time and they cannot communicate online" are 127, 194, 158 and 155 respectively.

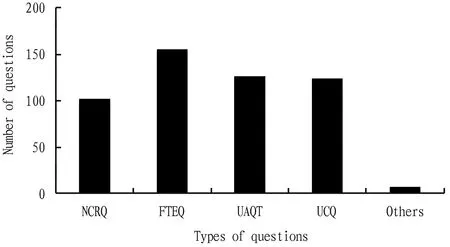
Note: NCRQ-no classification of real questions; FTEQ-few teachers explain questions; UAQT-unable to answer questions in time; UCO-unable to communicate online.

4 Strategy research and platform construction

According to the statistical analysis results of the questionnaire survey, the mathematics learning network platform for the postgraduate entrance examination can be constructed according to the real needs of the postgraduate candidates for the postgraduate entrance examination.

First, the choice of the year of the real questions for the postgraduate entrance examination: according to the statistical results of the questionnaire survey, more than 80% of the students want to review the real questions within ten years, and we can build a platform for the real math questions in postgraduate entrance examination within ten years.

Second, the setting mode of the real questions for the postgraduate entrance examination: according to the results of the questionnaire survey, the presentation way of the real questions for the postgraduate entrance examination is in the following order: year > mathematics type > mathematics course.Therefore, the network platform can refer to this order to classify the real mathematics questions for the postgraduate entrance examination.

Third, the communication and answering part: according to the results of the questionnaire survey, the main deficiencies of learning software are focused on online communication, timely answer and real question explanation, so we should consider setting up communication channels and answering part in the construction of the platform and build the real question explanation part.

This study takes the students who are interested in studying for graduate students as the research object, and analyzes the problems and real needs from the postgraduate candidates in mathematics learning through questionnaires and data analysis.A mathematical platform suitable for the postgraduate candidates should be built according to the survey results to help the postgraduate candidates to get twice the result with half the effort via the platform of postgraduate entrance examination.