基于改进Bi-RRT的移动机器人路径规划算法

崔春雷，陈诗豪，沈超航，李 锋

(广东交通职业技术学院，广州 510650)

0 引言

随着科技水平的进步，移动机器人越来越多的被应用到日常生活和工作的多种场景中，如目标的移动、探测和清洁等。 在移动机器人的研究领域中，路径规划算法属于重点研究方向。移动机器人路径规划问题可定义为: 在一个存在障碍物的空间里，给定移动机器人的起点和终点，在遵循时间最短、路径最优以及机器人运动学规律等一系列约束条件下，找到一条与障碍物无碰撞的路径。其中环境完全已知的规划问题属于全局路径规划，环境部分已知的规划问题为局部路径规划。常见的路径规划算法包括：A*算法、人工势场法、可视图法、概率路图算法、模拟退火算法、粒子群算法、蚁群算法、遗传算法等。以上算法往往需要事先对状态空间内的障碍物进行环境建模，导致计算复杂高，收敛速度过于缓慢。

LaValle等人在1998年提出了经典的快速搜索随机树 (RRT，rapid-exploring random tree)算法。RRT算法的搜索过程通过随机采样的方式把搜索树导向空白区，通过对空间中的采样点进行碰撞检测，从而避免了对空间的建模，该算法具有概率完备、计算量小、效率高等优点，能有效地解决高维空间以及复杂环境下的路径规划。然而 RRT 算法也存在一些不足，如需要在全图进行采样与搜索，会产生较多不相关的节点，从而增加了算法对内存的需求，并且也增加了相应的搜索时间，导致收敛速率较缓慢。针对RRT算法存在的缺陷，国内外众多学者纷纷进行了研究，提出了多种改进的RRT算法，如C.Urmson等在文献[16]发表了一个基于启发式的偏向算法，它将搜索树向目标点的位置进行了偏移，引导搜索树向目标区域生长，使路径搜索时间进一步优化。针对原始RRT算法中搜索得到的路径并非最优的问题，Karaman等在文献[17]中提出了具有渐进最优性的RRT*算法，该算法增加了父节点的重选和剪枝两个优化过程，但此算法也存在收敛速度较慢的缺点。为了提高搜索速度，Kuffne等人先后提出了RRT-connect算法和双向搜索树(Bi-RRT)算法。Bi-RRT算法从起点和终点同时出发，并行生成两棵RRT树，直至两棵树相遇，相较于RRT算法，Bi-RRT算法的收敛速度更快，但Bi-RRT算法采用的仍是RRT算法的随机节点扩展思想，导致路径搜索过程存在无目标导向性等缺点。

为了解决双向搜索树(Bi-RRT)算法在路径搜索时无目标导向性所导致的搜索效率过低的问题，本文提出了一种基于高斯采样的改进Bi-RRT算法。该算法在双向搜索的基础上，引入启发式搜索思想，采样点以一定概率以高斯分布的方式被约束在起点与终点周边，从而降低搜索的盲目性，提高了搜索的效率。通过仿真实验表明：在多种类型的复杂环境中，相对于基本的Bi-RRT算法，该算法搜索过程中扩展节点更少、收敛速度更快、路径相对更优。

1 Bi-RRT算法

RRT算法中随机树的生长缺乏目标导向性，导致大量冗余节点出现，算法的收敛速度较慢，Kuffner提出的双向RRT算法(Bi-RRT)则较好的解决了这个问题。Bi-RRT算法的主要过程为：以起始点

q

和目标点

q

为根节点分别构建两棵随机搜索树

T

和

T

，树

T

以

q

为树的根节点进行扩展，树

T

以

q

为树的根节点进行扩展，直到两棵树相遇。具体过程如图1所示，算法首先在整个搜索空间中生成随机扩展节点

g

，然后遍历随机树

T

和

T

，找出两棵树中距离

q

最近的节点并记为

q

，接着由

q

出发向

q

延伸步长

δ

得到新节点

q

，之后对新生成的节点

q

进行碰撞检测，若检测到

q

与障碍物碰撞则舍弃该节点,反之将

q

添加到树中，此时

q

是的

q

父节点；通过对上述过程进行迭代，使两棵搜索树不断向着对方扩展，直到两棵树各自的

q

之间的距离小于设定的阈值，此时认为两棵树相遇，路径规划成功。

图1 Bi-RRT算法节点扩展过程

相对于RRT算法，Bi-RRT算法效率更高搜索速度更快，但是Bi-RRT算法采用的仍然是 RRT算法的随机扩展节点思想，这也导致Bi-RRT算法和RRT算法一样存在着构型无目标导向性的缺点。

2 基于高斯采样的改进Bi-RRT算法

由于RRT算法和Bi-RRT算法在路径搜索过程中缺乏目标导向性，导致搜索过程的随机性较大，搜索树往往会扩展到远离我们所期待的目标区域的‘无用区域’，浪费了大量的计算资源，需要较长时间才能找到可行路径，且路径的代价往往较大。为此，本文提出了一种基于高斯采样的Bi-RRT算法，该算法的核心思想在于引入启发式搜索思想，随机扩展节点

q

不再以均匀分布的形式在搜索空间内随机出现，而是以一定概率以高斯分布的方式出现在目标点周边，这样搜索过程不但可以引导搜索树尽可能朝着目标区域前进，同时也保留了RRT算法的空间搜索能力，算法不仅提高了搜索效率，得到的路径也相对更优。

2.1 二维高斯分布性质分析

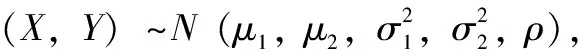
(1)

其中:

μ

,

σ

为分量

X

的期望值与标准差，

μ

,

σ

为分量

Y

的期望值与标准差，

ρ

值决定了

X

和

Y

的线性相关程度。这里假定

μ

=

μ

=0，

σ

=

σ

=5，来观察

ρ

取不同值时二维随机变量(

X

，

Y

)概率密度函数的图像。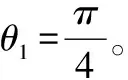

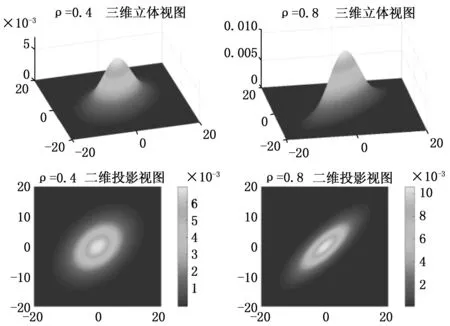
图2 ρ值与二维高斯分布概率密度函数图像关系

利用二维高斯分布的上述特性，我们引入启发式搜索策略，随机扩展采样点

q

不再以均匀分布的形式出现搜索空间内，而是被二维高斯分布函数约束在起点与终点周边区域，并引导搜索树朝着该区域方向生长。采用这种策略，在越接近目标点的空间，采样点

q

的出现概率越大，但是又不会把概率完全锁死在目标点本身，这样不但可以启发随机搜索树向着目标区域生长，提高搜索的效率，同时又能以一定的概率绕过障碍物。

2.2 高斯分布随机采样点的生成方法

本文算法采用双采样点策略，即用采样点

q

来引导随机树

T

的生长，用采样点

q

来引导随机树

T

的生长，而

q

和

q

则分别由以起点

q

和终点

q

为中心的两个二维高斯分布函数来分别来约束其生成。

图3 坐标系转换示意图

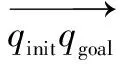
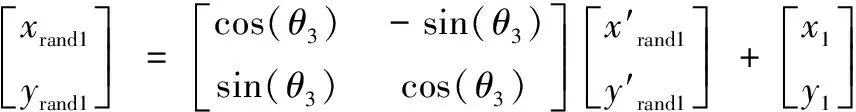
(2)

其中式(2)中的(

x

，

y

)为

q

在坐标系

OXY

中的坐标。按相同方法，我们可以生成以

q

中心点随机采样点

q

(

x

，

y

)。由图4可以看出随机采样点

q

主要分布在起点附近区域，且越接近点，其出现的概率越大，

q

则主要分布在终点

q

附近区域，越接近点

q

，其出现的概率也越大。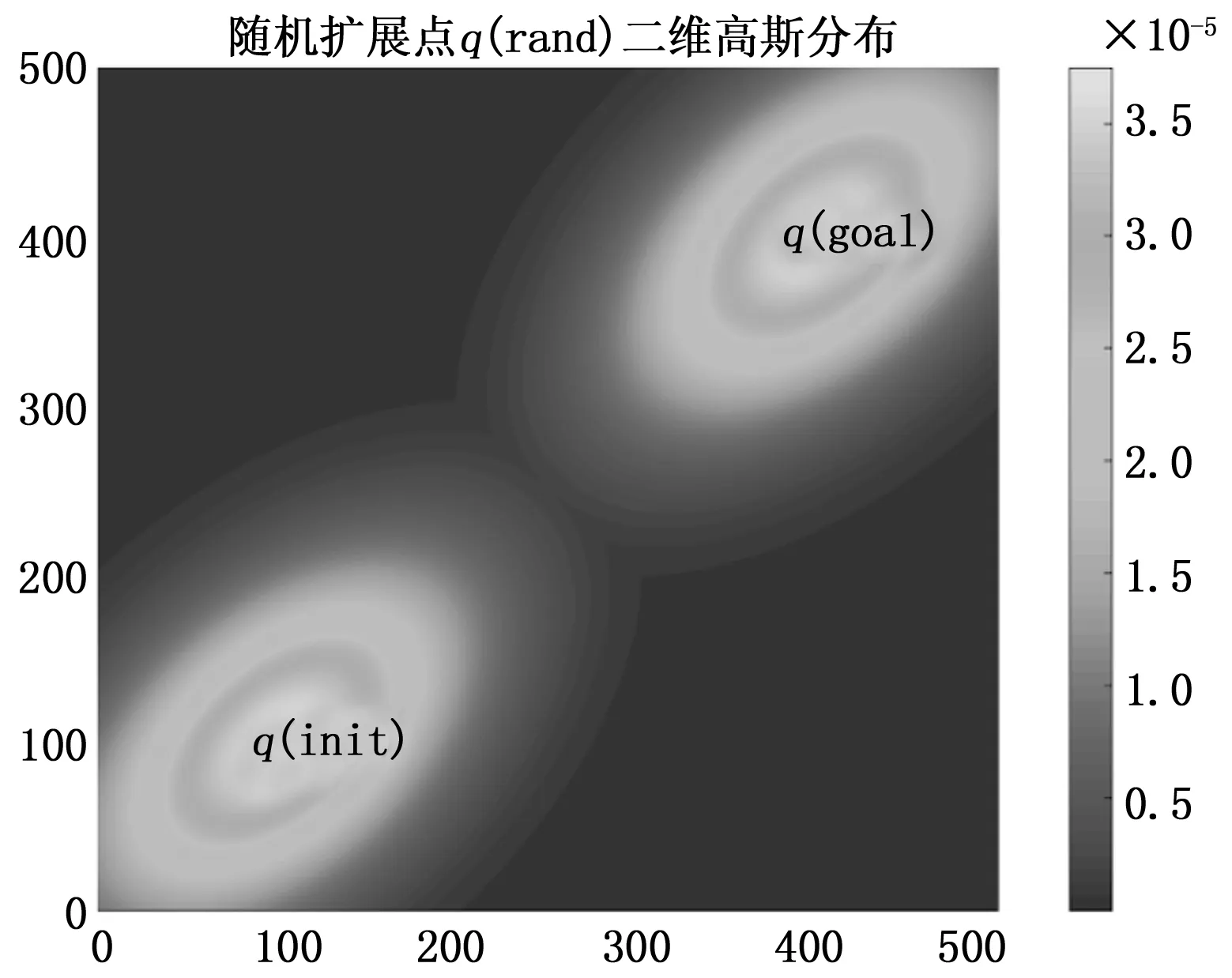

图4 随机采样点的概率分布示意图

2.3 改进Bi-RRT算法实现

算法1给出了改进Bi-RRT算法的伪代码，算法过程如下：首先以起点

q

和终点

q

为根节点分别构建随机树

T

和

T

(第1-2行)； 然后先以

q

为目标通过算法2生成随机点

q

用来引导

T

的生长，找到随机树

T

中离

q

最近的点

q

，以

q

为起点向

q

方向延伸步长

δ

生成叶子节点

q

，判断

q

与

q

之间是否存在障碍物，若不存在障碍物则将

q

作为

T

的子节点，并添加边(

q

,

q

)(第4-9行)；接着以

q

为目标通过算法2生成随机点

q

用来引导

T

的生长，按照相同的规则生成叶子节点

q

和边(

q

,

q

)(第10～15行)；最后如果

q

和

q

之间的距离小于设定的阈值

s

，且两者之间没有障碍物，则判定两棵树相互连接，路径规划完成(第16～17行)。

算法1：改进Bi-RRT算法伪代码

1)

V

←{

q

};

E

←

Φ

;

T

←(

V

,

E

);2)

V

←{

q

};

E

←

Φ

;

T

←(

V

,

E

);3)for

i

=1 to

N

do;4)

q

←sanple(

q

);5)

q

←Nearest(

T

,

q

);6)

q

←Steer(

q

,

q

);7)if ObstacleFree(

q

,

q

)then8)

V

←

V

∪{

q

};9)

E

←

E

∪{

q

,

q

};10)

q

←Sample(

q

);11)

q

←Nearest(

T

,

q

);12)

q

←Steer(

q

,

q

);13)if ObstacleFree(

q

,

q

)then;14)

V

←

V

∪{

q

};15)

E

←

E

∪{

q

,

q

};16)if (Dis tan ce(

q

;

q

)q

,

q

)) then17)Return(

T

,

T

)。为了平衡搜索过程中的随机性与目标导向性，随机点

q

的产生由3种机制共同决定，见公式(3)。设置两个目标偏置概率

p

和

p

，且满足0<

p

<

p

<1。

(3)

公式(3)中

p

为0～1之间的一个随机数；当

p

≤

p

时，

q

由2.2中的方法产生，即随机点

q

满足二维高斯分布特性；当

p

≥

p

时，随机采样点

q

为目标点

q

或

q

本身，这样可以充分利用目标点的信息，使得搜索树以一定概率朝着目标点方向快速前进；当

p

<

p

<

p

时，

q

符合均匀分布，这样可以让一部分随机点保留采样时的随机性，确保搜索过程在概率上的完备性，保障搜索树能跳出局部最优；算法2给出了公式(3)的伪代码。

算法2：随机点生成的伪代码

P

() //生成0～1之间的随机数

p

if

p

≤

p

q

=

q

. //

q

可取

q

或

q

else if

p

>

p

q

=

q

;//此时

q

按均匀分布else

q

=

q

;//此时

q

按二维高斯分布end if return(

q

)

3 仿真与分析

为了验证算法的有效性，在配置window10系统，主频3.40 GHz，内存16 GB的PC机上，采用Matlab 2020a对算法进行了编程仿真实验。仿真时设置的参数如下：仿真空间尺寸为500×500，起点

q

坐标为[1，1]，终点

q

坐标为[500，500]，步长

δ

=15，两树之间的距离阈值

s

=30，目标偏置概率

p

=0.6，

p

=0.9，二维高斯分布的参数为

σ

=

σ

=0

.

25

d

，

ρ

=0

.

5。

3.1 算法性能分析

仿真时按照障碍物的分布类型设置了3种有代表性的环境：简单环境、复杂环境、迷宫环境。分别在每一种环境下对Bi-RRT算法和基于高斯采样的改进Bi-RRT算法的性能进行对比。具体过程为：在每一种环境下，分别对两种算法各进行50次仿真测试，并使用路径长度(

L

)、扩展节点数目(

n

)、路径规划时间(

t

) 这3个参数作为性能指标，并求得这3个指标的50次仿真测试结果的均值，最后通过这3个指标对算法性能进行定量分析。

图5 环境1:简单环境

图6 环境2:复杂环境

图7 环境3:迷宫环境

图5为简单环境中两种算法的表现，图6为充满障碍物的复杂环境中两种算法的表现，图7为通道狭窄曲折的迷宫环境下两种算法的表现。从图5～7可以明显看出，基本Bi-RRT算法采样过程因为缺乏目标导向，采样点分布过于随机，导致搜索树往往会在“无用区域”浪费过多资源，产生过多的无用节点，而本文改进算法引入启发式搜索思想，充分利用了目标点的位置信息，让随机点不再“盲目”出现，而是以高斯分布的形式出现在目标点附近的空间，搜索过程所需的随机采样点的数量更少，效率也更高。

如表1所示，对图5这种简单环境，本文算法的额外的扩展节点更少，路径也更平滑，路径长度也更小。对图6这种充满密集障碍物的复杂环境，本文算法的优势更加明显，相对于基本Bi-RRT算法，平均规划时间缩短了43.9%，平均扩展节点数目减少了41.4%，路径长度优化了8.1%。对图7这种富有挑战性的充满狭窄通道的迷宫环境，相对于基本Bi-RRT算法，改进算法的平均规划时间缩短了30.9%，平均扩展节点数目减少了27.2%，路径长度优化了2%。通过定量分析可知，本文提出的改进Bi-RRT算法的路径搜索时间更短、扩展节点更少、路径更优。

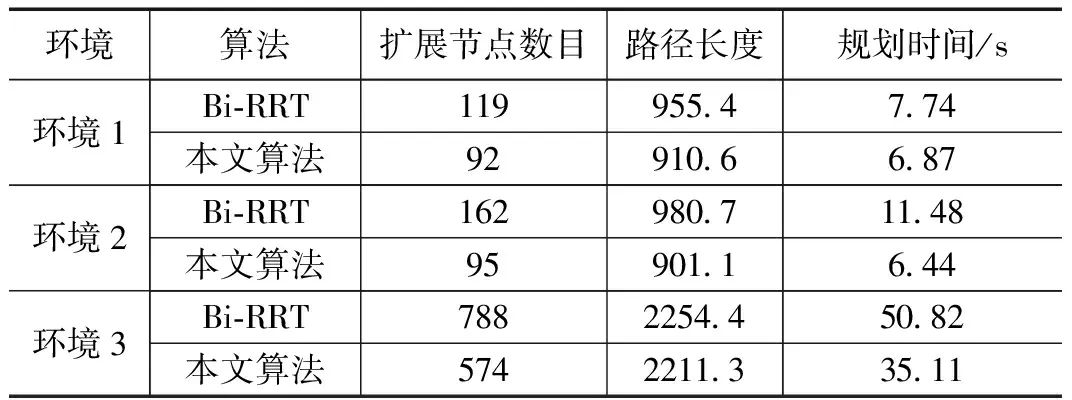
表1 不同环境下算法性能对比

3.2 目标偏置概率对算法性能的影响

改进算法中目标偏置概率

p

,

p

对算法的运行效率有着重要影响。由公式(3)可知采样点由3种机制共同产生，分别在概率

p

=

p

下按二维高斯分布出现，在概率

p

=

p

-

p

下按均匀分布出现，以概率

p

=1-

p

把起点(或终点)作为采样点，显然

p

+

p

+

p

=1。为了简化问题，保持

p

=0

.

1不变，此时

p

=0

.

9-

p

，这里

p

显然表示的是按高斯分布出现的采样点占总的采样点数的百分比。下面来分析概率

p

的值对算法性能的影响，这里仍然以图6中的复杂环境作为测试环境，在保持其他仿真参数不变的情况下，测试

p

取不同值时算法性能的表现。图8为仿真测试得到的平均节点数目随概率

p

变化的曲线，从图中可以看出，平均节点数目随着概率

p

的增加而减少，当

p

=0

.

7附近时达到极小值。图9则为平均规划时间随概率

p

变化的曲线，与图8的规律一致，这里规划时间也随着概率

p

的增加而减少，当

p

=0

.

7时规划时间达到最小值，之后随着

p

的增加规划时间又有所上升。可见，概率

p

较小时，即按照高斯分布出现的采样点占比少时，算法效率会降低；另一方面概率

p

如果取到0

.

9，即所有随机点都按照高斯采样时，则又因为缺少了自由采样带来的随机性，算法效率也会降低，只有当

p

取到合适值时，算法的效率才最高。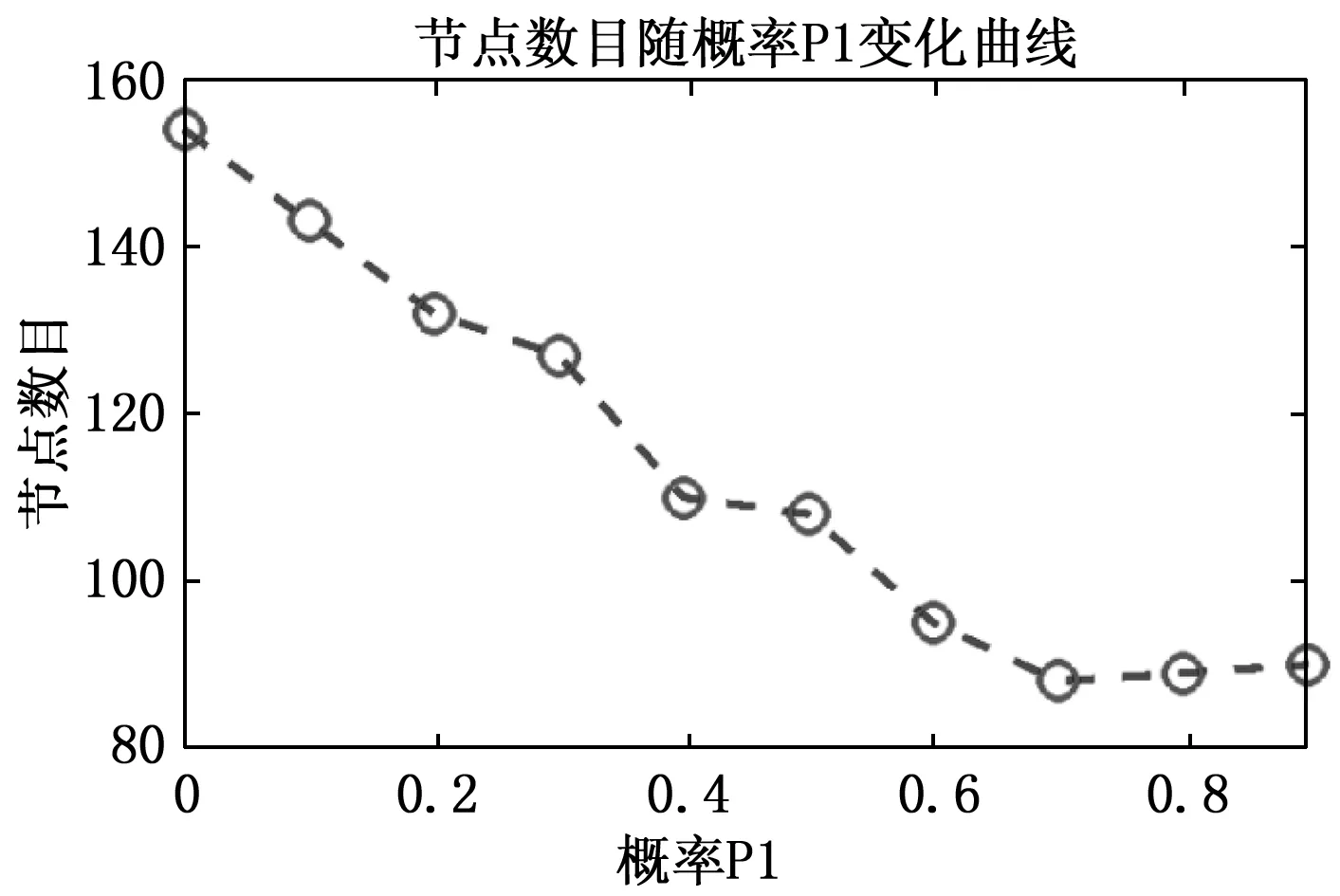

图8 平均节点数目随概率变化曲线

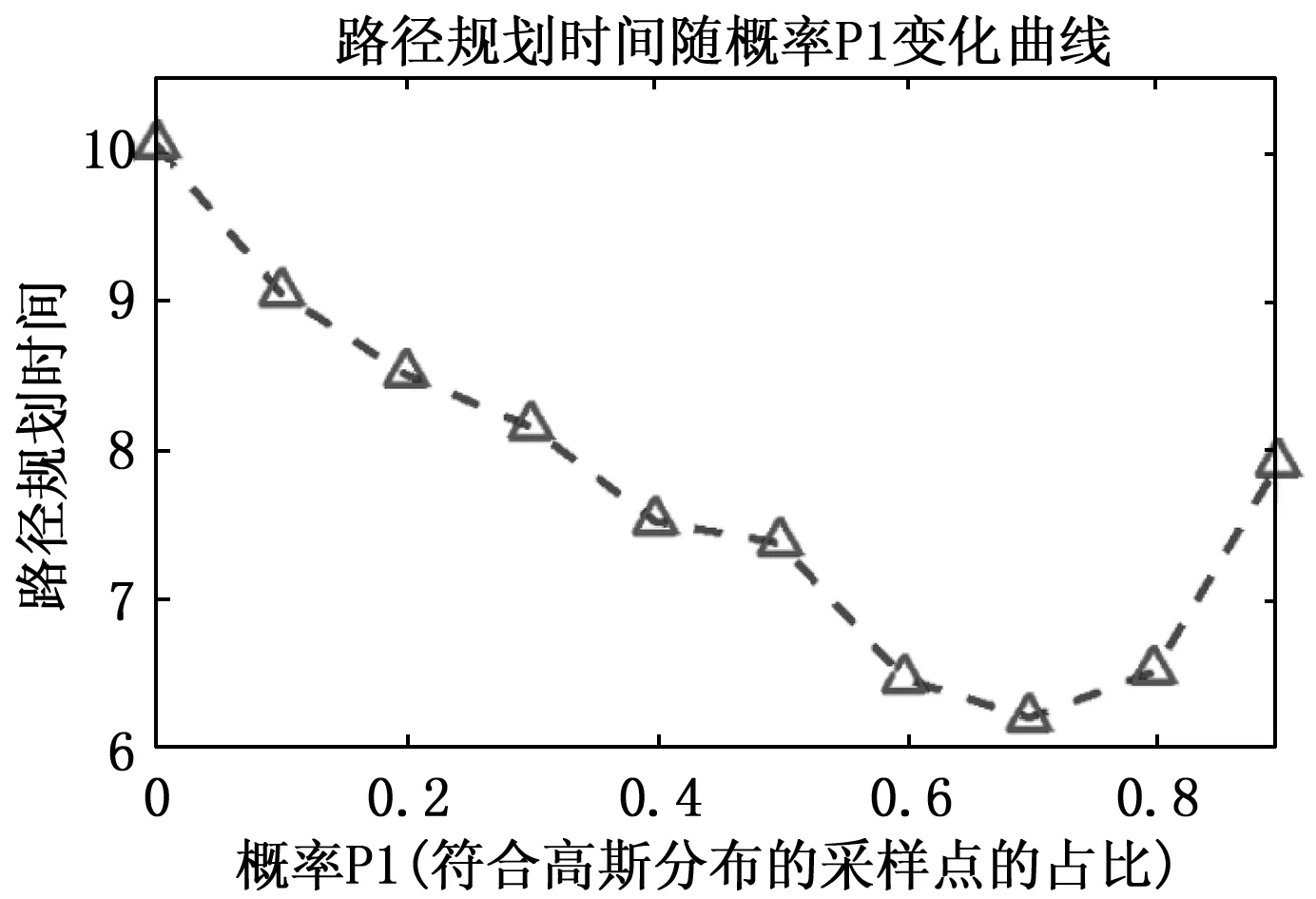
图9 平均规划时间随概率变化曲线

4 结束语

为了改进Bi-RRT算法的效率，本文提出了一种改进Bi-RRT算法，该算法分别以机器人的起点和终点为概率分布的中心，构建二维高斯分布概率密度函数，并用该函数约束随机采样点的生成，同时也保留一部分均匀分布的采样点，通过这些具有目标启发性的采样点来引导两棵搜索树快速向目标点生长并相遇。该算法在保证搜索过程概率完备性的前提下，提高了寻径的效率和质量，相对于基本的Bi-RRT算法，本文算法在应对复杂环境、迷宫环境等环境时的表现更佳，如在复杂环境下规划时间缩短了43.9%，扩展节点数目减少了41.4%，路径长度优化了8.1%，最后分析了目标偏置概率对算法性能的影响，找到了使算法效果最优时对应的高斯分布采样点的占比。未来可以考虑将本文算法结合RRT*算法，并应用到3维以上的高维空间中的路径规划问题。