基于逆序层优先的柔性综合调度算法

谢志强 王 茜

(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150000)

1 引言

传统的生产制造过程，将加工[1,2]和装配[3,4]作为两个独立的阶段，对问题的研究主要针对零部件的批量加工，例如针对大批量生产环境的flow shop调度问题[5,6]和针对多品种小批量生产环境的job-shop调度问题[7,8]。随着社会多元化需求的增加，多品种小批量的订单逐渐增多，在这种多元化需求环境的驱动下，需要一种新的生产调度模式，满足人民个性化定制型产品的需求。这样，综合调度[9]应运而生，它将产品的加工过程和装配过程统一为加工过程，将复杂产品映射为虚拟加工树。由于同时考虑了工序间的顺序约束和装配约束，综合调度问题在缩短产品制造周期、提高生产系统效率方面，具有重要的研究意义和实际应用价值。另外，随着加工技术、自动化技术的发展，柔性制造系统和数控加工中心等带有一定柔性的生产系统在实际企业生产中扮演着越来越重要的角色，柔性作业车间调度问题更加符合实际生产问题。因此，本文研究具有柔性设备选择的树状结构产品综合调度问题。

柔性综合调度问题较传统的车间调度问题和一般的综合调度问题更为复杂，也是一类典型的NP难问题[10]。目前，对综合调度问题研究的文献还相对较少，且主要求解单车间一般综合调度问题[11,12]等。 针对柔性综合调度问题，在基于启发式规则的相关解决方案中，谢志强等人[13]提出了一种考虑设备无关延迟约束的综合柔性调度算法。谢志强等人[14]从设备找工序的角度出发，提出了一种基于设备驱动的综合柔性调度冲突调解算法。Birgin等人[15]提出了一种基于链表的柔性综合调度算法，并且在此基础上进一步提出了一种基于集束搜索的柔性综合调度算法。谢志强等人[16]提出了一种设备驱动和实质路径的动态并行综合柔性调度算法，该算法兼顾了设备驱动和动态实质短路径策略的优点，提高了设备利用率和并行处理效率。针对柔性综合调度问题，在基于智能优化算法的相关解决方案中，赵诗奎等人[17]提出了一种基于虚拟零部件级别分区编码的产品综合调度算法。该算法将产品的各零部件设置级别，按级别进行分区编码，该种编码方式保证了初始解的可行性，但其编码方式存在缺点，即有遗漏最优解的风险。Lei等人[18]提出了一种基于工序关系矩阵表的综合调度算法，该算法首先为产品建立一个工序关系矩阵表，随后基于该表设计了相应的编码规则和进化算子。由于综合调度问题中复杂优先顺序约束条件的存在，导致已有的各种编码方法和进化算子均已失效，进而使得智能优化算法在综合调度问题中的应用受限。总体来说，研究柔性综合调度问题的相关文献还相对较少。

在上述求解柔性综合调度问题的相关算法中，均考虑正向调度，即从叶节点开始调度，直至根节点调度完毕，则代表产品调度加工完成。在正向调度的解决方案中，当某一工序有多个紧前工序时，难以合理安排这些相关工序，进而影响产品总加工时间。因此，本文采用逆序调度的思想，从根节点开始调度，这样可以简化某一工序存在多紧前工序的约束条件，便于合理安排各工序。最终将调度产生的逆序调度方案转换为正序调度方案。

2 问题描述

在传统的柔性Job-shop调度问题中，工序间的总体约束结构呈线状，而柔性综合调度问题中调度对象的总体工艺结构图呈树状结构，这使得在树状结构产品柔性综合调度问题的调度过程中，需要考虑工序间的协调和同步问题，从而使问题的目标函数得到优化。在该问题中，某产品的工艺加工树如图1所示，每个工序由3部分构成，即工序名、加工设备集以及对应的加工时间，箭头的指向规定了工序间的加工顺序。树状结构产品柔性综合调度问题的数学模型可以描述为：由n道工序 {oi}1≤i≤n构成的树状结构复杂单产品，需要在m台设备上进行加 工，工 序oi的 可 加 工 设 备 集 为{Mi}1≤i≤n ⊆{1,2,...,m}并 且Mi ̸=∅，pik为 工 序oi在 设 备k ∈Mi上的加工时间。si和ci分别表示工序oi的开始加工时间和完工时间。xli=1表示工序ol是工序oi的工艺紧前工序；yik=1表示工序oi在设备k∈Mi上进行加工；zij=1表示在同设备上加工的工序oi和oj，工序oi为工序oj的设备紧前工序，即工序oj在工序oi加工完成之后才开始加工。因此本问题的数学描述为

图1 产品A加工工艺树

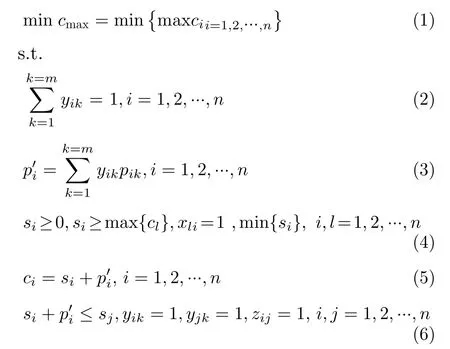
其中，本问题的调度目标是合理安排各工序以使产品的完工时间尽可能短，目标函数如式(1)所示。式(2)表示每道工序要被分配到某1台且只能1台机器上进行加工；式(3)表示工序oi的加工时间，式(4)为工序oi的开工时间，即工序oi要在合理的条件下尽早开始加工；式(5)为工序oi的完工时间。式(6)表示同一台设备上连续加工的两道工序，后一道工序的开工时间不能早于前一道工序的完工时间。

3 算法设计

对于一棵产品工艺加工树，由于根节点加工完毕代表整个产品加工完毕，即根节点工序加工完成为最终加工目的。首先加工叶节点最后加工根节点会导致加工过程中工序有多个紧前约束条件，而首先加工根节点，可减少相关工序节点的加工约束。本文采用逆序调度的思想，即首先加工根节点，直到叶节点加工完毕，该产品调度结束。为了便于算法描述以及后续相关策略的设计，本文首先给出如下定义：

定义1 目标工序：调度过程中，将当前正在安排的某一工序称为目标工序。

定义2 待调度工序集：即将调度的某一层工序组成的集合。

定义3 拟加工时间：对于可在超过3台设备上加工的工序，本文去掉最长加工时间和最短加工时间，然后计算剩余加工时间的平均加工时间作为该工序的拟加工时间；对于可在少于两台设备上加工的工序，直接计算该时间集的平均加工时间作为该工序的拟加工时间。

定义4 伪紧前工序：由于本文采用逆序调度，原本某一工序的紧后工序成为该工序的紧前工序，称为伪紧前工序。

定义5 伪紧后工序：由于本文采用逆序调度，原本某一工序的紧前工序成为该工序的紧后工序，称为伪紧后工序。

定义6 伪紧后路径长度：按拟加工时间计算时，由目标工序的所有伪紧后工序加工到叶节点的总时间的最大值。

定义7 伪紧前路径长度：由根节点工序开始加工，目标工序的伪紧前工序的实际完工时间。

定义8 总路径长度：目标工序的伪紧前路径长度，伪紧后路径长度以及拟加工时间之和。

定义9 子孙节点：工序的后代子孙节点，例如工序A15的子孙节点为工序A9，A10，A3，A4，A1。

对于图1所示的复杂产品柔性工艺加工树，按照上述定义，我们计算其拟加工时间和伪紧后路径长度如图2所示，例如对于工序A15，其拟加工时间为20，伪紧后路径长度为70。

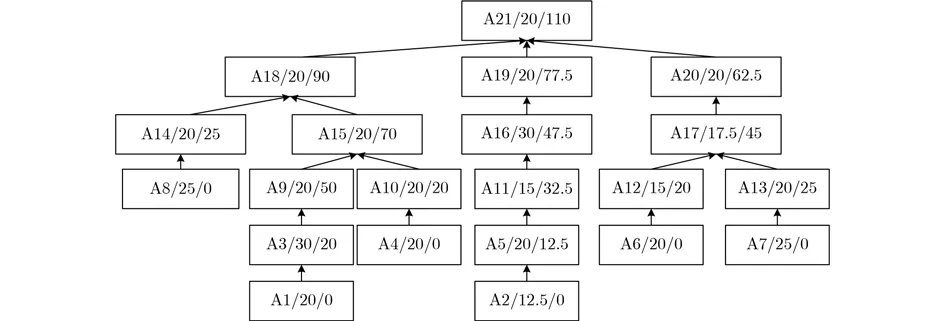
图2 图1所示产品各工序拟加工时间和伪紧后路径长度

3.1 逆序层优先策略

本文提出逆序层优先的策略，对各工序按层进行调度。首先，为每个工序设置其所在的层数，即规定根节点所在的层为第1层，随着后续工序其深度每增加1层，所在层数加1。然后，将第i层上的所有工序放入工序集合Oi中作为第i层的待调度工序集，例如O4={A8, A9, A10, A11, A12, A13}。最后，按照层数递增的顺序，依次对各层工序集进行调度。由于本文采用逆序调度加工的思想，缓解了正序调度时，某一工序存在多个紧前工序，难以确定目标工序开工时间的问题。另外，同层工序优先调度，可以最大化的使同层工序并行加工。

3.2 动态拟长路径策略

对于某层待调度工序集Oi={o1, o2, ···, on}，设其伪紧前工序集为Pi={p1, p2, ···, pn}，伪紧前工序的结束时间即伪紧前路径长度为PEi={pe1, pe2,···, pen}，拟加工时间集合为A_Ti={a_t1, a_t2,···, a_tn}，伪紧后工序集为Si={s1, s2, ···, sn}，伪紧后路径长度Ri={r1, r2, ···, rn}，计算第i层待调度工序集中各工序的总路径长度Ti=PEi+A_Ti+Ri，例如第j个工序的总路径长度为pej+a_tj+rj。

由于本文采用逆序调度的思想，目标工序的伪紧前工序的结束时间，为目标工序最早可加工时间，在不考虑设备占用的情况下，本文以各工序的总路径长度，来估计目标工序子孙节点的最终完工时间，路径长度越大，说明其对应的子孙节点的完工时间越晚，所对应的产品完工时间越晚。因此，本文优先调度路径长度大的目标工序，由于目标工序的伪紧前工序的结束时间不同，导致每次计算总路径长度时所得结果不同，因此称该策略为动态拟长路径策略。

该策略的主要思想是，按待调度工序集中各工序的总路径长度对各工序进行降序排列，优先调度总路径长度值大的目标工序；当总路径长度值相同时，优先调度拟紧后路径长度大的工序；当拟紧后路径长度值相同时，优先调度拟紧后工序个数多的工序；当紧后工序个数相同时，优先调度拟加工时间值大的工序；再相同时，随机选择某一工序调度。

3.3 设备选择策略

对于一棵柔性工艺加工树，某一工序可能可以在多个设备上加工，但不同加工设备所需加工时间可能不同。为了尽可能地减少总加工时间，本文尽量为目标工序选择加工用时短的设备进行加工。即针对目标工序oj，获取该工序的伪紧前工序完工时间，获取该工序的可加工设备集并按加工时间从小到大排序，若可最短加工时间所对应的设备在目标工序的伪紧前工序完工时刻空闲，则将目标工序分配至该设备上加工；否则，按序选择将目标工序安排至完工时间最早的设备上加工。 若存在多个设备加工时间相同，则优先选择目标工序完工时间早的设备进行加工。由于目标工序伪紧后工序是在目标工序的基础上进行加工，其伪紧后工序的开工时间由该工序的结束加工时间决定，则选择早结束方案所对应的设备加工对缩短整体加工时间有利。

3.4 设备抢占策略

本文采用逆序调度的思想，从根节点开始，按层序依次调度每层待调度工序集中的工序。由于同层工序间，不存在紧前紧后约束关系，为了充分提高设备占用率，缩短产品完工时间，本文考虑设备抢占情况，以优先加工可早加工的目标工序。

由于首先调度根节点工序，因此，其开工时间我们规定为0。对于目标工序oj，在确定了加工设备进行调度时，若其最早可加工时刻设备空闲，则考虑将该工序放置该时刻进行加工，若该时刻有后续加工工序，则将其移至目标工序完工时刻进行加工。

3.5 基于完工时间翻转的调度方案转换策略

由于本文采用逆序调度的思想，所产生的调度方案为逆序调度方案。为了将逆序调度方案转换为正序调度方案，即产品的调度从叶节点开始，本文给出了一种基于完工时间翻转的调度方案转换策略。假设已知待转换方案的产品最终完工时间，各工序的逆序开工时间和逆序完工时间。则本文所述的转换策略的具体方法为：首先，将各工序在逆序调度时的开工时间和完工时间分别减去当前方案的产品完工时间；然后，将各工序所对应的结果取反，即将各个开工时间和完工时间值变成非负数；最后将各工序对应的开工时间和完工时间交换即可获得正序调度时各工序的调度时刻表。注意，在转变为正序调度方案后，若某一工序的所有紧前工序已加工完成，且当前工序开始加工时刻之前存在空闲时间段，则该工序可以向前移动。但是，无论是在正序调度方案中还是逆序调度方案中，产品的最终完工时间是不变的。因此，本文并没有考虑工序的移动情况。

3.6 算法总体设计

本文所述的基于逆序层优先的柔性综合调度算法具体执行步骤如下所述，算法总体流程图如图3所示。

图3 算法总体流程图

步骤1 输入设备和产品加工信息，计算工序拟加工时间，伪紧后路径长度等属性信息。

步骤2 执行逆序层优先策略，为各工序设计层优先级，并按其所在的层数将其加入至不同的层待调度工序集，并将集合按层序升序排列，假设一共有m层工序，则最终一共产生m个工序集，i=1。

步骤3 判断i是否大于m，若是则执行步骤4；否则，执行步骤5。

步骤4 执行基于完工时间翻转的调度方案转换策略，将逆序调度方案，转换为正序调度方案，算法结束。

步骤5 假设当前待调度工序集为Oi，则执行动态拟长路径策略，将待调度工序集中各工序排序。

步骤6 判断待调度工序集是否为空，若为空，则i=i+1，跳转至步骤3；否则，执行步骤7。

步骤7 获取待调度工序中的首个工序作为目标工序，并将其在待调度工序集中移除。

步骤8 按设备选择策略为目标工序确定加工设备。

步骤9 按设备抢占策略确定目标工序开工时间，跳转至步骤6。

4 复杂度分析

设工序总数为n，可加工设备总数为m。初始时，算法需要计算工序拟加工时间以及其伪紧后路径长度，在计算目标工序拟加工时间时，需要执行m次操作，一共有n道工序，因此其时间复杂度为O(n×m)。计算工序伪紧后路径长度时，首先获取其伪紧后工序的路径长度，然后加上当前工序的拟加工时间，共有n道工序，因此，其时间复杂度为O(n)。本算法主要执行以下操作：

(1) 逆序层优先策略。该操作需要遍历所有工序，将各工序加入不同的逆序待调度工序集，需要执行n次操作，因此，逆序层优先策略的时间复杂度为O(n)。

(2) 动态拟长路径策略。对于当前逆序层待调度工序集Oi，设其工序个数为ni，对于每道工序我们需要计算其总路径长度，即执行两次加法操作，总共执行2×ni次操作，时间复杂度为O(ni)。然后需要按总路径长度对当前工序集工序进行排序，时间复杂度为O(nilog2ni)。最坏情况下，ni=n，因此，动态拟长路径策略的时间复杂度为O(nlog2n)。

(3) 设备选择策略。对目标工序来说，在为其选择加工设备时，最坏情况下需要考虑所有可加工设备，即执行m次操作。因此设备选择策略的时间复杂度为O(n×m)。

(4) 设备抢占策略。确定目标工序开工时刻的时候需要确定其最早可加工时刻是否空闲，若空闲则抢占至该时刻进行加工，总共需要判断n次，因此时间复杂度为O(n)。

(5) 基于完工时间翻转的调度方案转换策略。在转换过程中，需要将各工序在逆序调度时的开工时间和完工时间分别减去当前方案的产品完工时间；然后，将各工序所对应的结果取反变成非负数；最后将各工序对应的开工时间和完工时间交换即可获得正序调度时各工序的调度时刻表。因此，该策略的时间复杂度为O(n)。

综上所述，本文所提算法的时间复杂度取上述各项操作的最大值，即所提算法的时间复杂度为O(nlog2n)。

5 实例对比分析

本文所述算法不针对任何具体产品，对所有算例均实用。为了进一步阐述上述算法的执行步骤，本节对图1所示产品工艺加工树进行调度加工，并将调度方案与已有的主流的解决柔性综合调度问题的算法进行对比。

计算各工序相关属性信息，例如拟加工时间、伪紧后工序径长度等。

初始时，第1层待调度工序集为O1={A21}，仅包含一个元素，即根节点工序A21，其伪紧前工序集P1={}为空，因此，该层工序最早可加工时刻为PE1={0}，加工时间为t1={(M1,M2,M4)/(20,25, 15)}，拟加工时间集合A_T1={20}，由设备选择策略为其选择用时最短的设备M4进行加工，其完工时间为时刻15，第1层待调度工序集调度结束，第1层工序结束时间为e1={A21/15}。

第2层待调度工序集为O2={A18, A19, A20}，其伪紧前工序集P2={A21, A21, A21}，最早可开始加工时刻为PE2={15, 15, 15}，其加工时间集t2={(M1, M3, M4)/(20, 15, 25), (M2, M3,M4)/(15, 20, 25), (M3, M4)/(20, 20)}，拟加工时间集合A_T2={20, 20, 20}，伪紧后工序集合为S2={(A14, A15), (A16), (A17)}，当前层待调度工序集的伪紧后路径长度集为R2={90, 77.5, 62.5}，则当前待调度工序集各工序所对应总路径长度为O2= PE2+A_T2+R2={A18/125, A19/112.5,A20/97.5}，对O2按其所对应的总路径长度按降序进行排列的并按序进行调度，最终调度顺序为{A18, A19, A20}。对于工序A18，按设备选择策略中短用时优先原则，将其分配至设备M3进行加工；对于工序A19，按设备选择策略中短用时优先原则，将其分配至设备M2上进行加工；对于工序A20，按设备选择策略中最早结束时间原则，确定其加工设备为M4。第2层待调度工序调度完成，其结束时间集e2={ A18/30, A19/30, A20/35}。

第3层待调度工序集为O3={A14, A15, A16,A17}，其伪紧前工序集P3={A18, A18, A19,A20}，最早可开始加工时刻为PE3={30, 30, 30,35}，其加工时间集t3={(M1, M3, M4)/(20, 20,15), (M1, M3, M4)/(20, 15, 25), (M2, M4)/(20,40), (M2, M4)/(15, 20)}，拟加工时间集合A_T3={20, 20, 30, 17.5}，伪紧后工序集合为S3={(A8), (A9, A10), (A11), (A12, A13)}，当前待调度工序层的伪紧后路径长度为R3={25, 70,47.5, 45}，则当前待调度工序集各工序所对应总路径长度为O3= PE3+A_T3+R3={A14/75,A15/120, A16/107.5, A17/97.5}，对O3按其所对应的总路径长度按降序排列并按序进行调度，最终调度顺序为{A15, A16, A17, A14}。对于工序A15，按设备选择策略中短用时优先原则，确定其加工设备为M3；对于工序A16，按设备选择策略中短用时优先原则，确定其加工设备为M2；对于工序A17，按设备选择策略中最早结束时间原则，其加工设备为M4；对于工序A14，按设备选择策略中最早结束时间策略，其加工设备为M1。第3层待调度工序调度完成，其结束时间集e3={A14/50,A15/45, A16/50, A17/55}。

第4层待调度工序集为O4={A8, A9, A10, A11,A12, A13}，其伪紧前工序集P4={A14, A15, A15,A 1 6, A 1 7, A 1 7}，最早可开始加工时刻为PE4={50, 45, 45, 50, 55, 55}，其加工时间集t4={(M1, M2, M3, M4)/(25, 25, 30, 25), (M1, M3,M4)/(20, 20, 45), (M2, M3, M4)/(25, 20, 20),(M1, M2, M4)/(10, 15, 25), (M1, M3, M4)/(15,15, 35), (M1, M2, M4)/(15, 20, 40)}，拟加工时间集合A_T4={25, 20, 20, 15, 15, 20}，伪紧后工序集合为S4={(), (A3), (A4), (A5), (A6), (A7)}，当前待调度工序层的伪紧后路径长度为R4={0, 50,20, 32.5, 20, 25}，当前待调度工序集各工序所对应总路径长度为O4= PE4+A_T4+R4={A8/75,A9/115, A10/85, A11/97.5, A12/90, A13/100}，对O4按其所对应的总路径长度按降序排列并按序进行调度，最终调度顺序为{A9, A13, A11, A12,A10, A8}。对于工序A9，按设备选择策略，确定其加工设备为M3；对于工序A13，按设备选择策略中短用时优先原则确定其加工设备为M1；对于工序A11，按设备选择策略中短用时优先原则，确定其加工设备为M1，由于在先调度A13时，设备M1上将产生5时间段的空隙，因此，根据设备抢占策略，前移调整工序A11；对于工序A12，按设备选择策略，将其安排至设备M3上加工；对于工序A10，按设备选择策略，其加工设备为M4；对于工序A8，按设备选择策略中短用时优先原则，其加工设备为M2。第4层待调度工序调度完成，其结束时间集e4={A8/75, A9/65, A10/75, A11/60,A12/80, A13/75}。

第5层待调度工序集为O5={A3, A4, A5, A6,A7}，其伪紧前工序集P5={A9, A10, A11, A12,A13}，最早可开始加工时刻为PE5={65, 75, 60,80,75}，其加工时间集t5={( M2, M4)/(30, 30), (M2,M3, M4)/(30, 15, 20), (M1, M2, M4)/(15, 20, 25),(M1, M3, M4)/(20, 20, 20), (M1, M2, M3,M4)/(20, 25, 25, 35) }，拟加工时间集合A_T5={30, 20, 20, 20, 25}，伪紧后工序集合为S5={ (A1), (), (A2), (), ()}，当前待调度工序层的伪紧后路径长度为R5={20, 0, 12.5, 0, 0 }，当前待调度工序集各工序所对应总路径长度为O5= PE5+A_T5+R5={A3/115, A4/95, A5/92.5, A6/100,A7/100}，对O5按其所对应的总路径长度按降序排列并按序进行调度，最终调度顺序为{A3, A7, A6,A4, A5}。对于工序A3，按设备选择策略，确定其加工设备为M2；对于工序A7，按设备选择策略中短用时优先原则，其加工设备为M1；对于工序A6，按设备选择策略中短用时优先原则，确定其加工设备为M3；对于工序A4，按短用时原则及最早结束时间原则，其加工设备为M4；对于工序A5，按设备选择策略中短用时优先原则，确定其加工设备为M1。第5层待调度工序调度完成，其结束时间集e5={A3/105, A4/95, A5/110, A6/100,A7/95}。

第6层待调度工序集为O6={A1, A2}，其伪紧前工序集P6={A3, A5}，最早可开始加工时刻为PE6={105, 110}，其加工时间集t6={ (M1, M2,M4)/(15, 20, 35),(M1, M2)/(10, 15) }，拟加工时间集合A_T6={20, 12.5}，伪紧后工序集合为S6={(), ()}，当前待调度工序层的伪紧后路径长度R6={0, 0 }，当前待调度工序集各工序所对应总路径长度为O6= PE6+A_T6+R6={A1/125,A2/112.5}，对O6按其所对应的总路径长度按降序排列并按序进行调度，最终调度顺序为{A1, A2}。对于工序A1，按设备选择策略中短用时原则，确定其加工设备为M1；对于工序A2，按设备选择策略中最早结束时间原则，确定其加工设备为M2。第6 层待调度工序调度完成，其结束时间集e6={A1/125, A2/125 }。

针对图1所示产品工艺加工树，经过本文所述算法，逆序调度甘特图如图4所示，产品完工时间为125工时，经本文所述的基于完工时间翻转的调度方案转换策略，正序调度方案如图5所示。

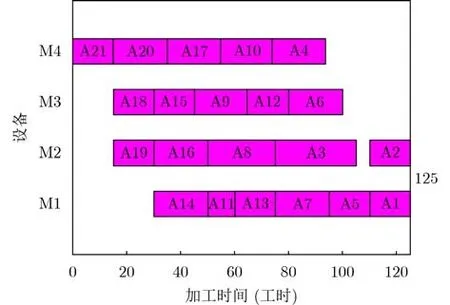
图4 应用本文所提算法产生的逆序调度方案

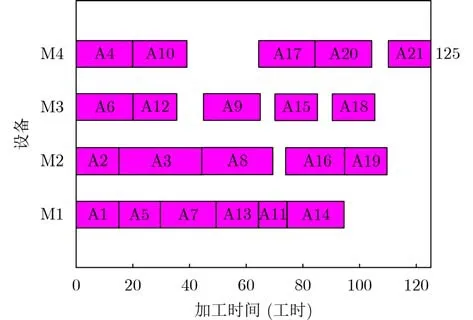
图5 应用本文所提算法产生的正序调度方案

为了验证所求调度方案的优越性，本文采用主流的解决柔性综合调度问题的算法对图1所示产品进行调度加工，其中，采用基于设备驱动的综合柔性调度冲突调解算法[14]所得到的调度结果如图6所示，总加工时间为140工时；采用基于设备驱动和实质路径的动态并行综合柔性调度算法[16]所得到的调度结果如图7所示，总加工时间为135工时。采用基于链表调度的柔性综合调度算法[15]所得到的调度结果如图8所示，总加工时间为155工时。经过对比可以发现本文所得完工时间均优于上述算法所得结果。

图6 基于设备驱动的综合柔性调度冲突调解算法调度结果甘特图

图7 基于设备驱动和实质路径的动态并行综合柔性调度算法调度结果甘特图

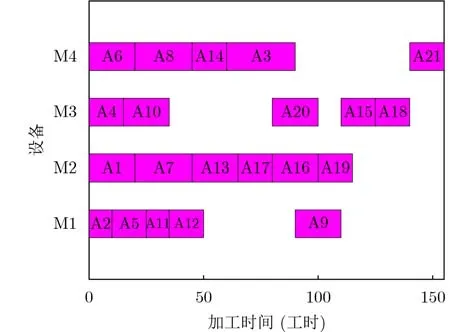
图8 基于链表调度的柔性综合调度算法调度结果甘特图

6 结束语

本文针对解决复杂产品柔性综合调度问题时，正向调度导致调度结果不理想的问题，提出了一种基于逆序层优先的柔性综合调度算法。首先提出了逆序层优先策略，从根节点开始调度，减少了多紧前工序的约束条件；其次提出了动态拟长路径策略，优先调度对产品完工时间影响大的工序；然后提出了设备选择策略和设备抢占策略，尽量为目标工序选择加工用时短的工序且尽量提前加工，有利于缩短产品完工时间；最后提出了基于完工时间翻转的调度方案转换策略，将逆序调度方案转换为正序调度方案，便于实际调度。该算法在不提高算法复杂度的前提下，提高了设备利用率，缩短了产品完工时间。