改进神经网络BP算法及其应用

李越男 徐振平 马心池

摘要：BP神经网络由于其结构简单、能够自适应、自己学习，有着优越的非线性映射能力，使得它成为当下神经网络应用中最为面面俱到的一种。但从数学角度看，标准BP神经网络采用最速梯度下降法，所以收敛的速度较为缓慢，轻易就会陷入局部极小得不到全局最优、训练次数要达到一定的数量、学习效率不容乐观等缺点。文章以BP神经网络作为研究对象，从四个方面来介绍BP神经网络的整体框架，首先对BP网络的原理和实现步骤进行了系统概述，其次针对其缺点提出了从增加动量项、自适应调节学习率和优化神经网络结构进行改进方法，再次介绍BP算法相关的应用领域，最后进行总结。

关键词：PB算法;学习率;误差;梯度下降法

中图分类号：TP311        文献标识码：A

文章编号：1009-3044（2022）11-0086-02

1 引言

BP（Back Propagation） 网络[1]在1986年，由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是应用最广泛的神经网络模型之一。BP神经网络是一种按误差反向传播（简称误差反传）训练的多层前馈网络，把这个算法称为BP算法。

BP算法包括信号的正向传播和误差的反向传播两个过程。信号的前向传播从输入层经过隐含层到输出层得到一个正向传播的预测值。若预测值和实际值不相符合，则进行反向传播，误差由输出层经过隐含层向输入层反向传播，根据误差值修改权重，继续迭代不断修改权重，直到达到最优。标准BP算法采用的是最速梯度下降，存在收敛数度慢，容易陷入局部极小、训练次数多、学习效率低等缺点。

由于BP算法自身存在的缺点，不少学者也对BP算法做出了大量的研究，如可以使BP神经网络进行动态的全参数自调整学习[2]，将动量法和批处理方法结合对BP算法改进[3]。本文主要针对标准反向传播BP算法结构原理、实现步骤、改进方式及其应用这四个方向进行深入研究。对于BP算法所存在的缺点，讨论从不同的方向上的改进措施。旨在让读者更好地了解与应用BP算法，并能做出进一步的深入研究。

2 反向传播BP算法的原理与实现步骤

反向传播的BP算法的基本思想就是通过计算输出层与期望值之间的误差来调整网络参数，从而使得误差变小。它的基本原理是梯度最速下降法，它的中心思想是调整权值使网络总误差最小。

多层网络运用BP学习算法时，实际上包含了正向和反向传播两个阶段。将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使误差信号最小。也就是说神经网络是一种求解权重w的算法，分为信号“正向传播（EP） ”求损失，也就是求得预测值和实际值之间的差值。“反向传播（BP） ”传回误差，根据误差值修改每层的权重w，继续迭代。其中每一个神经元都经过了线性变化和激活函数的变换。

BP网络由输入层、隐藏层、输出层组成。以三层感知器为例，其結构如图1。

BP算法-EP过程：

在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望输出，则转入反向传播。

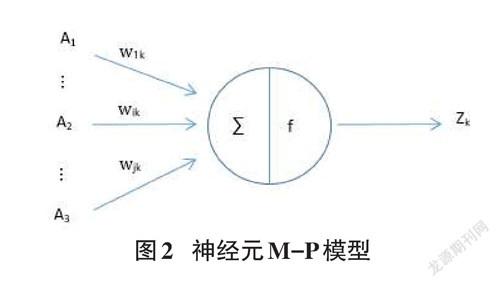
其中输出层A1～An是特征属性，也可以进行多项式的扩展，如A2。隐层中每一个节点都是一个神经元，神经元M-P模型包含两个部分如图2所示，神经元包含[w]x+b的线性变换和f（wx+b）的激活函数转换两个部分。激活函数的变化乘以其对应的权重作为，下一层神经元的输入。输出层的节点也是包含这两部分。最后Z1～Zk就是经过正向传播函数变换后输出的预测值。

① s是实际值;Z为预测值;则s-Z为误差;[w]为某个节点的权重;y表示某个节点的输出;m个神经元

② 1～l个输出层节点的误差之和，也就是神经网络输出层的整体误差。

③ 输出层误差向前进行回传，输出层节点进行[fnetk]激活函数的变换，则将[Z]=[fnetk]带入（1） 式后得到（2） 式。

④ 反向传播过程中，根据神经元的线性变化和激活函数的变换可以得出：

[Zk]=[fnetk]=[fj=1mwjkyj]=[fj=0mwjkfnetj]=[fj=0mwjkfi=1nvijxi] （4）

⑤ 为了使误差E越来越小，可以采用随机梯度下降算法进行[w]和[v]的求解，即让求出的w和[v]使误差E最小，[η]是初始化时给定的固定学习率。

[Δwjk=-η∂E∂wjk  j=0，1，2，…，m;k=1，2，…，l]  （5）

[Δvij=-η∂E∂viji=0，1，2，…，n;j=1，2，…，m]  （6）

3 BP算法的改进方向

由于标准BP算法采用的是最速梯度下降，因此存在收敛数度慢，容易陷入局部极小得不到全局最优、训练次数多、学习效率低等缺点。查看相关文献，国内外已经提出了不少改进算法，针对其缺点，比较具有代表性的改进方法有增加动量项、自适应调节学习率和优化神经网络结构等。

增加动量项改进BP算法，主要是针对误差曲面可能会出现又窄又深曲线引起训练中的误差来回震动。增加动量项公式如下：

[Δwt=ηδX+aΔwt-1] （7）

[α]为动量系数，一般有[α∈0，1]

权值[w]的修正由两部分组成，第一，是由当前的梯度所决定，权值修正量[Δwt]和误差信号成正比和某层的输入X成正比。第二，是与上一次的修正量[wt-1]确定，而上一次的修正量取多少呢？取[α∈0，1]，公式后面一项叫作动量项，其阻力作用，可以减少训练中震荡次数，增加收敛速度。

自适应调节率改进BP算法，针对初始化时给定的学习率[η]在整个实验过程中不变，但误差曲面较为平坦时，希望权值W调节得更快一些，对学习率[η]进行调节。由于[η]和梯度成正比，所以设一初始学习率，若经过一批次权值调整后使总误差增大，则本次调整无效，且[η=ηββ<1];若经过一批次权值调整后使总误差减小，则本次调整有效，且[η=θηθ>1]。

优化神经网络结构改进BP算法，是针对隐含层的层数与隐节点的个数。实际求解问题时，网络输入层和输出层节点个数一般根据问题的性质设定好了，但是隐节点的个数如何选择，还是缺乏理论指导，往往根据经验的积累和试探的方法。实践证明，对于简单的映射关系，在网络精度达到要求的情况下，选择少量的隐含层层数;对于复杂的映射关系，可以通过增加隐含层层数来确保映射关系的正确实现。

查阅相关文献，BP神经网络与遗传算法、进化计算、人工免疫算法、模拟退火算法等新的算法进行结合，提出了一些新的混合算法，还有将BP算法和模糊数学相结合突出模糊神经网络。这些结合使得BP算法进一步得到发展。

4 BP算法的应用

近年来，BP算法在多个领域都获得了较好的发展。与其他学科技术相融合，对二者都有非常好的良性循环，如在土木工程应用中，对受损结构进行受损与否和受损部位定位与检测等;在电力工业应用中，对光伏发电系统输出功率短期预测模型[4];在化工学科中，在牵扯到非线性因素建模时的表现优异;在预测模型中，对多种情况的数据预测都体现了它的优势所在，对不动产业售价与热度评估，对影响因素与售价和热度之间进行分析，如基于BP神经网络对上市公司财务预警建立模型[5];同时在风险预警预测方面也有着非常广泛的应用，如地震、海啸检测等，为以后的自然灾害检测方面提供了新方法新思路。

虽然BP算法目前应用面较为广泛，但并不是一成不变的，BP网络自身还存在着缺陷和需要改进之处，如学习收敛的速度并不理想、学习效率不够稳定、可能会有局部极小的出现等。目前对于BP神经网络，国内外的许多研究人员也提出了各种对BP算法进行的改进，如启发式和与新理论相结合的方法，随着技术的日益进步，算法会不断得到优化，BP神经网络也会有更好更广泛的未来。

5 总结

本文系统地介绍了反向传播BP算法的原理与实现步骤，针对标准BP算法目前存在的缺点对BP算法的常见改进方向做了详细阐述。通过增加动量项、调整自适应学习率和优化神经网络结构等方向来对BP算法做进一步的改进。由于BP神经网络算法还存在许多问题，传统的改进方法大多是对数值的优化进行改进。在未来的深入学习研究中，有望深入研究，提出新的改进方法或应用于新的领域。

参考文獻：

[1] David E. Rumelhart， Geoffrey E. Hinton & Ronald J. Williams Learning representations by back-propagating errors[J].Nature，1986.

[2] 李晓峰，刘光中.人工神经网络BP算法的改进及其应用[J].四川大学学报（工程科学版），2000，32（2）：105-109.

[3] 陈桦，程云艳.BP神经网络算法的改进及在Matlab中的实现[J].陕西科技大学学报，2004，22（2）：45-47.

[4] 丁明，王磊，毕锐.基于改进BP神经网络的光伏发电系统输出功率短期预测模型[J].电力系统保护与控制，2012，40（11）：93-99，148.

[5] 杨淑娥，黄礼.基于BP神经网络的上市公司财务预警模型[J].系统工程理论与实践，2005，25（1）：12-18，26.

收稿日期：2022-01-12

作者简介：李越男（1996—） ，女，湖北荆州人，研究生在读;通信作者：徐振平，男，副教授，博士;马心池，男，研究生在读。