以主题教学提升学生核心素养
韩艳琼


【摘 要】 本文简述了主题教学的概念,探究了以主题教学提升学生核心素养的策略,以期为高中数学教学提供借鉴.有了主题教学的铺成,核心素养在数学学科起到的效果,涵盖了以分析、逻辑推理、建模、运算、直观想象、抽象设想为首的六个方面.基于数学基础,加强了学生们各方面的知识进取能力,其中关于“数列”教学尤为突出.
【关键词】 主题教学;核心素养;数列单元
在“数列”主题单元教学中体现和落实数学核心素养,要深入挖掘教材,明确“数列”单元涉及的数学核心素养,在分析课程标准、教材内容、学生学情的基础上对“数列”单元开展科学的教学设计,落实数学核心素養,在引导学生掌握数列概念和性质,并懂得迁移应用知识解决数列求项以及求和问题的同时,培养学生的核心素养,引导学生深入理解并有效养成数学抽象、逻辑推理、数学运算以及数学建模等核心素养,学会用数学的眼光看世界.
1 主题教学概述
1.1 主题教学概念
主题教学,是指教师引导学生对教材章节主题涉及的综合知识、重要概念、学习方法、常见题型等进行深入探究,指导学生紧扣单元主题知识开展深度的思维探索,增强对单元主题知识的深度体验,并在潜移默化中实现对学生核心素养的良好培养.与常规教学方法相比,主题教学重视探究过程,能拓宽学生对课程知识的认识广度和深度,能巩固学生对课程知识的理解掌握,增强学生对知识的迁移应用能力,还能有效培养其核心素养[1].
教师在开展数学教学的实践过程中,对主题教学进行应用,应突破逐节备课的方式,着眼于单元教学主题,开展跨章节教学,引导学生深入理解单元主题大概念,对单元主题知识形成良好的整体性把握,增强学生的数学探究能力,并培养学生的数学核心素养[2].
1.2 基于核心素养的高中数学单元主题教学的特点
基于核心素养的高中数学单元主题教学具有如下特点:(1)整体性.整体性是指教学内容具有完整性和内在逻辑性.基于核心素养的单元主题教学具有整体性特点,强调从单元整体上凸显知识系统性.数学教师开展单元整体教学,要深入挖掘教材,从整体视角对单元主题教学内容进行精准把握,并在单元主题教学中,增强学生的数学探究能力,培养其数学核心素养.(2)高效性.单元主题教学知识具有紧密的内在联系,通常以由浅入深的顺序编排知识内容,对此,教师开展单元主题教学,要秉持循序渐进的原则,增强教学的高效性和有序性,引导学生实现良好的学习迁移.(3)组合性.教师要紧扣单元教学主题,优化组合教学资源,并考虑学生的差异性特点和个性化学习需求,梳理教学知识的内在逻辑,对教学知识进行优化组合.(4)以学生为本.教师开展单元主题教学,要秉持以学生为本的理念,尊重学生在教学中占据的主体地位,根据学生的学习和认知特点确定教学目标,从整体上对教学知识进行建构,在增强教学效果的同时,实现对学生核心素养的有效培养.
2 以主题教学提升学生核心素养的策略
2.1 在单元备课中明确“数列”教学单元涉及的核心素养
高中数学教材“数列”单元教学内容涵盖数列概念、等差数列、等比数列以及数列应用的等内容.教师在开展“数列”单元主题教学前,应做好单元备课,从整体上梳理“数列”单元教学内容,明确其中涉及的核心素养[3].
在“数列”单元教学中,对数列概念、数列性质进行建构,均有赖于良好的数学抽象.对数列概念进行建构,涉及两次数学抽象,对应函数模型;对等差数列概念进行建构,涉及两次抽象,对应一次型函数模型;对等比数列概念进行建构,涉及两次数学抽象,对应指数型函数模型.对函数模型进行构建后,即可从函数角度对数列进行研究,有助于开拓学生的数学视野,并研究数列具备的单调性特点和周期性特点[4].
在“数列”单元教学中,“数列”知识体系蕴含了典型的逻辑推理方法,即从特殊到一般.等差数列以及等比数列各自的性质、通项公式,均可利用从特殊到一般的逻辑推理方法,进行归纳推理而完成建构.“数列”单元内容蕴含的类比推理也极为丰富.对实数加法、实数乘法等进行类比,对等差数列以及等比数列各自的项进行加法、乘法类比即可获取新的等差数列和等比数列.
在“数列”单元教学中,蕴含着丰富的数学运算.例如,数列通项、数列求和等运算均需要合理选择算法.数列结构不同,决定其求和运算选用的方法也不同,常见求和方法有分组法、裂项法以及错位相减法等.
在现实中,资产折旧、购房贷款以及存款利息等生活现象均是数列原型,通过数列模型,即可实现对现实问题的有效解决.“数列”单元本身即体现了建模过程:对现实问题情境进行描述、对数学模型进行构建、对实际问题进行解决.
对“数列”单元教学内容进行整体梳理,可知该单元主要涉及如下数学核心素养:(1)数学抽象.具体表现:对数列、等差数列以及等比数列等数学概念进行抽象,构建数列性质命题和数列模型,进而搭建系统完整的数列知识架构.(2)逻辑推理.具体表现:发现并提出各类数列性质、通项以及求和公式等数学命题;增强学生的各类逻辑推理能力,包括归纳演绎能力、类比能力等.(3)数学运算.具体表现:对数列实质进行理解;掌握数列涉及的各类运算法则,包括通项运算、求和运算等.(4)数学建模.具体表现:将具体情况作为依据,从中抽象出数列等数量关系.
2.2 聚焦核心素养做好教学设计
教师开展“数列”单元主题教学,要聚焦数学核心素养,做好教学设计,在教学过程中,要创设良好的教学情景,引导学生对“数列”知识内容进行深入思考,增强对“数列”知识的情感体验,在潜移默化中培养学生的情感体验[5].
2.2.1 从数学抽象的高度建构数列概念
概念是对事物本质属性的认识.概念教学要注重引导学生对事物本质进行抽象.在开展“数列”单元教学的过程中,要从数学抽象的高度,建构数列概念.在开展“数列”单元教学的过程中,教师可引导学生对类似概念进行梳理,帮助其形成概念思维.教师可创设数列概念的教学情景,引导学生找出清晰明确的学习线索,帮助学生实现“概念抽象”[6].
例如 笔者创设了如下教学情境:在历史上,人们很早即用数列对一类简单事物进行描述:13世纪意大利出现的“斐波那契数列”,是1,1,2,3,5,8,13,21,…;我国古代《庄子》中提到“一尺之棰,日取其半,万世不竭”,其用数列表示,即为1,12,14,18,116,….笔者向学生提问到上述数列模型的共同特点是什么?可从哪些方面对数列进行认识?
要引导学生对抽象过程进行体会.抽象,是指将一类对象所包含的物理属性全部排除,找出其共同性质,抽象是建构数学概念的核心环节.具体包括如下过程:(1)观察、比较、归纳,从特例中找出共同点,通过归纳得出共性;(2)构建正确表征,以恰当语言对之进行描述,实现对表征的数学符号化;(3)完成对共性的抽象后,在更大范围中对本质进行检验,通过举列子实现概念具体化[7].教师可引导学生抽象过程进行反思,掌握抽象过程涉及的各项步骤.
2.2.2 从逻辑推理的高度引导学生提出问题
逻辑推理是从命题和事实出发,遵循逻辑规则,对新命题进行构建的思维过程,包括演绎推理方式和合情推理方式.发展提升学生的逻辑素养,有赖于具体的推理过程.教师要从逻辑推理高度引导学生深入思考如何开展逻辑推理,而不是仅关注逻辑推理形成的结果.
例如 教师创设如下教学情境
(1)某剧场共有30排座位,第一排共有20个座位,第二排有22个座位,第三排有24个座位,随后每排座位都比前一排座位多2个,那么各排座位数分别是多少?
学生回答 20,22,24,26,28,30……
(2)《庄子》有言“一尺之棰,日取其半,万世不竭”,假设“一尺之棰”是一份,那么每日剩下的部分是多少?
学生回答 1,,,,
(3)“一去二三里,烟村四五家,亭台六七座,八九十枝花.”在这首诗里,都包括哪些数字?
学生回答 1,2,3,4,5,6,7,8,9,10.
问题 上述例子的共同特点是什么?
(学生经过小组讨论后,)
学生 它们都是一系列数.
教师 能对以上的数的顺序进行对调吗?为什么?
学生 不可以.一旦对调数字的顺序后,表达的意思就变了.
教师 综合上述例子可知,它们都是按照相应的顺序组成的数,也就是数列.对数列的定义进行归纳:数列是指按照一定的顺序排列的数.在此过程中,学生的数学抽象能力即得到良好培养.
教师要通过引导学生对已掌握的数学知识进行反思,学习逻辑推理,总结推理过程,逐步增强自身的数学核心素养.例如,在对等差数列通项公式进行归纳、猜想和证明后,引导学生对如下問题进行反思:(1)如何对等差数列通项公式进行归纳?(2)通过归纳、类比得出的结论是否正确?为何要对结论进行证明?学生在对归纳过程进行反思时,能提炼出归纳包含的基本步骤:观察、比较、概括总结、检验[8].
2.2.3 从理解算理的高度对题组进行设计
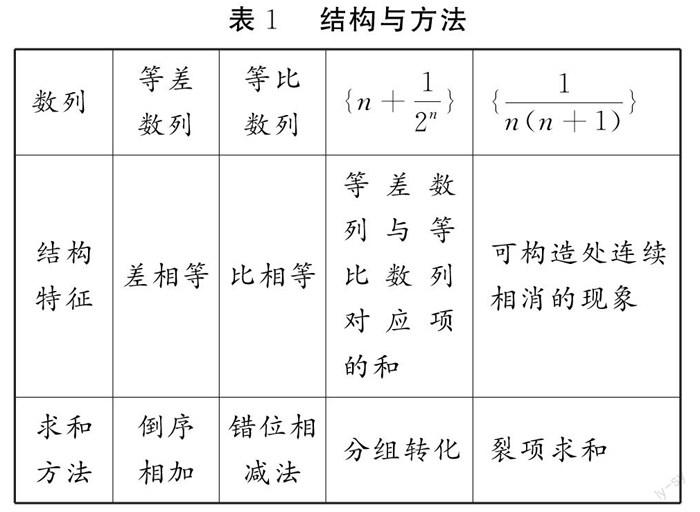
在“数列”单元教学中,等差数列与等比数列在通项与求和方面具有不同的方法.对此,在结束单元教学后,可通过变式题组,从理解算理的高度对题组进行设计.例如,对数列求和的方法进行比较,可得出下表:
根据上述表格,引导学生对如下问题进行思考:(1)上述方法为什么不同?(2)基本的思考方向是什么?据此加深学生对数列运算的理解.学生会认识到数列结构的不同决定了数列求和的方法不同,对此,要通过比较对运算路径进行合理选择.
2.2.4 从强化“数学建模”的高度加强对数学知识的应用
数列原型大量存在于现实生活中,对此,教师要从强化“数学建模”的高度加强对数学知识的应用.教师应借助实际问题开展知识导入;
通过开放性的问题引导学生提出问题,引发学生爆发式的思考,延申作者的想象力,最后研究研究数学建模对解决数学问题的帮助和意义,首先是要对习题找出关键性的要点描述,然后代入所有给出的要点,构建数学模型解决数学问题.最后总结,引导学生学习建模的知识点,加深对该知识点的印象,通过一次次的数学建模,让学生加强跟数学之间的了解,提高学生解决数学问题的能力.完成对“数列”单元的教学后,教师可引导学生通过整体回顾,加深对数列知识结构的体会,增强对数学建模的情感体验,提高数学建模的能力[9].
3 概念教学设计案例之《数列》
3.1 教材分析
《数列》内容是学生对数列的首次接触,教师可引导学生整理归纳已有知识,为数列学习夯实基础,例如集合知识、函数知识能促进学生对数列的学习.数列可描述离散现象,这是基础且常见的数学模型,能在多种领域加以应用,学好《数列》内容,能为后续等差数列和等比数列的学习夯实基础.
3.2 学情分析
学生在对数列进行学习前,已经学习了集合知识和函数知识,且了解了集合、函数的研究方法,遵循“概念—表示—性质—应用”的主线开展学习探究,是学习《数列》的基本方法.学生具备较好的数学思维,可对抽象知识展开自主探究.
3.3 教学目标
基于对教材和学情的分析,制定如下教学目标:(1)知识与技能:与生活实例相结合,对数列定义进行抽象概括,了解数列表示方法、通项公式等性质,根据通项公式将数列的项列出,根据列出的数列的项,对其通项公式进行归纳.在此过程中,培养学生的数学抽象和逻辑推理素养.(2)过程与方法:对数列概念进行概括,学习从特殊到一般的数学思想,对数列性质进行推导,学习类比推理,体会数学知识的整体性,实现对类比推理基本方法的掌握.在此过程中,培养学生的数学运算、逻辑推理、数学抽象以及数学建模素养[10].(3)情感态度与价值观:引导学生对数列性质进行探索,体会数学思想方法蕴含的逻辑性.
3.4 教学设计
3.4.1 创设情境
从现实生活中选取教学实例,创设生动形象的教学情境,激发学生对数列的学习探究兴趣,加强数列知识与现实生活的联系,引导学生利用数列知识解决现实问题,锻炼并增强学生的抽象思维能力,培养学生的数学建模素养.
教师创设储蓄问题情境,引导学生利用数列知识进行数学建模以解决实际问题,在此过程中锻炼并增强学生的数学建模素养.
设置问题情境如下 某银行存款年利率如下表1所示:
问题1 按照上表所示储蓄方式,每月固定存入金额100元,持续三年,到期本息共计多少元?
问题2 按照上表所示储蓄方式,每月存入固定金额b元,持续三年,到期本息共计多少元?
上述两个问题的設计意图,是运用等差数列前n项和,先从具体存款数字入手,对表格信息进行观察,对三年后本息进行计算,再将具体数字转化为字母b,抽象思考该存货模式下,三年后本息的数学模型.
3.4.2 教学评价
在数列教学过程中,要创设生活化的数学课堂,采用多元化的教学方法,引导明确问题的发展方向,对数学知识的整理归纳,并整理出相关知识点的串联.锻炼数学思维,找出和问题的根本,发现题型难点,归纳解决难点的思路等,引导学生对数学全局的掌握,最后根据整理对现实性数学问题解决方式,加强数学思想对学生的渗透,在潜移默化中培养学生的数学思维.
4 结语
综上所述,基于核心素养的高中数学单元主题教学具有整体性、高效性、组合性等特点.教师以主题教学提升学生核心素养,要在单元备课中明确“数列”教学单元涉及的核心素养,并通过从数学抽象的高度建构数列概念、从逻辑推理的高度引导学生提出问题、从理解算理的高度对题组进行设计、从强化“数学建模”的高度加强对数学知识的应用等策略聚焦核心素养做好教学设计,在取得良好教学成效的同时,实现对学生核心素养的有效培养.
参考文献:
[1]张婷.开展主题教学 提升核心素养——以高中数学必修五“数列”一章为例[J].西藏教育,2018(01):27-29.
[2]张格波.提升核心素养,我们可以怎样做?——以苏教版教材“数列”单元的教学为例[J].中学数学教学参考,2019(10):12-16.
[3]王华民,阮必胜,朱翠.立足教材,培养学生数学核心素养的教学实践——以“数列”为例[J].中国数学教育,2018(10):38-41.
[4]郑荣坤.高中数学教学中对学生核心素养的培养——以“等差数列”教学为例[J].中学数学研究(华南师范大学版),2018(12):28-30.

