预测股票市场走势的模型评估

王源　李俊刚

摘要：近年来，随着股票市场的不断发展，包含大量股票价格信息的数据库也越来越被重视，对于股票预测方法的探索也从未中断。文章通过对上证指数的历史数据进行收集，采用移动平均法、自回归综合移动平均、长短期记忆网络三种算法对股票走势进行预测，判断哪种算法预测的精确度最高。实验证明，LSTM算法的拟合程度更高，均方根误差 RMSE 最小。该算法能够通过学习股票历史数据的变化，利用其内部的选择记忆性，更准确地实现短期股票的预测。

關键词：移动平均法;自回归综合移动平均; 长短期记忆网络

一、引言

我国股票市场经过 30 多年的发展， 形成了一个庞大的股票信息数据库，股票市场变化规律的掌握、股票市场走势的预测，成为投资者们关注的焦点，投资者们若能对股价进行较为准确的预测，便能够使得所作决策更为正确，这样可以大大降低亏损的风险，进而使得收益最大化。因此，探索股票市场中的规律变得越来越重要。本文用三种不同的模型分别预测股票市场走势，通过对比来探索不同模型的优缺点及准确度，得出预测最为精确的模型。

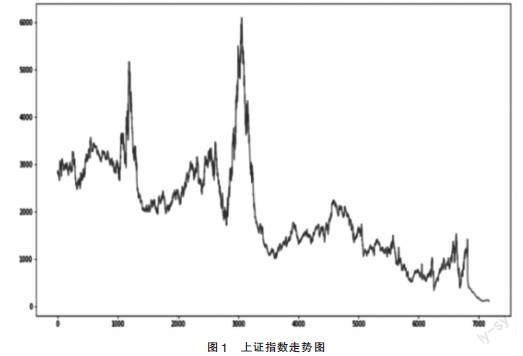
首先，根据1990年12月20日至2020年4月30日股票收盘价做出现阶段上证指数走势图（见图1），发现股票收盘价随起伏波动，但其长期趋势呈下降趋势。根据上证指数7178条观测值，按照4：1划分，将1990年12月20日起之后的5742条观测为训练集，测试集为剩下的1436条观测。分别用三种模型对其走势进行预测，并进行评估。

二、移动平均法对股票价格走势预测

（一）理论介绍

在日常生活中，虽然算术平均法能够代表某类数据的平均水平，但该法对数据变化趋势的反应却不是那么的明显。有时候，某些蕴含时间序列的数据往往会受到周期变动和随机变动的影响，因此数据的起伏会比较大，其发展变化趋势也不能够清晰地展现出来，所以在基于算术平均的基础上逐渐发展出移动平均法，通过移动平均来消除此类因素的影响，进而显示时间序列长期的发展趋势。在此次预测中，假设每一期的数据在计算过程中具备的作用相同，所以使用移动平均中的一次移动平均来进行计算。

一次移动平均即取时间序列的N个观测值，并加以平均，然后依次滑动到将所有的数据计算完毕，这样便会得到一个平均值序列。

设时间序列为y1，y2，…，yn;n为样本容量

则其计算公式为：

M■■=■（t≥N）（1）

其中：M■■为第t期的一次移动平均值;

N是移动平均的项数（也称步长）。

由以上计算可以得到一个时间序列的移动平均序列。并且可以看出移动平均的作用在于将其他因素的干扰消除掉进而将数据进行修匀使其平滑，所以移动平均相比于算术平均更能显露时间序列的长期趋势，进而可用于趋势分析及预测。

通常来说，假如时间序列的周期性变化和趋势性变化不是那么明显，则可以用某期的一次移动平均值作为下一期的预测值，其预测模型为：

y^t+1=M■■（2）

式（2）中，y^t+1代表第t+1期的一次移动平均值。

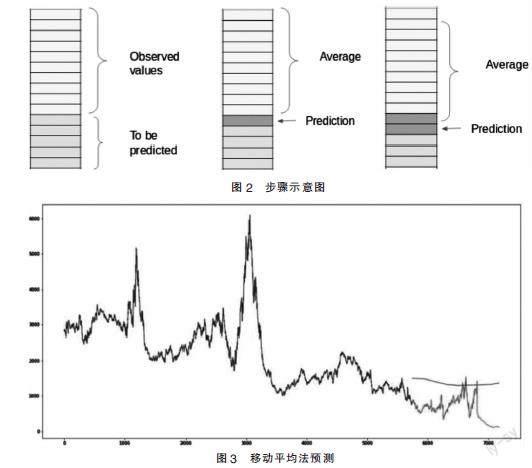
利用一组先前观测值的平均值作为每天的预期收盘价，对于后续每个新时间，在考虑预测值时，都从集合中删除最早的观测值，并加入上一个观测值。步骤示意如图2所示。

（二）预测结果图并进行分析

利用移动平均法对上证指数进行拟合，拟合结果如图3所示。

均方根误差也成为标准误差，定义为i=1，2，3，…n，在有限测量次数中，均方根误差的表达式为Re=■，n为测量次数，di为测量值和真实值的偏差。

计算得出RMSE值近似793，且从图3中可以看出，测试集的走势为先缓慢下降，然后平稳。而实际的数据走势是先平稳再上升，现阶段有下降趋势。拟合效果不是很理想。

三、自回归综合移动平均（ARIMA）对股票价格走势预测

（一）理论介绍

自回归综合移动平均（ARIMA）是一种时间序列模型。ARIMA模型建模本质上是一种面向数据的探索性方法，ARIMA模型本身具有一定的灵活性，还有适应数据本身结构的适当性。通过偏自相关函数和自相关函数，可以近似地模拟出时间序列的随机性质。并从中发现随机变换、趋势、周期模式和周期分量及序列相关等方面的信息，并在一定精度水平上对未来值进行预测。

ARIMA模型的表达式为：

Yt-φ0-φ1Yt-1- …-φpYt-p=at-θ1at-1-…-θqat-p（3）

其中，at，at-1，…at-p是均值为0，方差为ε2的平稳白噪声。φ1，φ2，…φp是自回归系数，θ1，θ2，…θp是移动平均系数。p和q分别是自回归模型和移动平均模型的阶数，模型被命名为具有模型自回归阶p和模型移动平均阶q的自回归移动平均序列，简称ARMA（p，q）。

当q=0时，为AR（p）序列;

当p=0时，为MA（q）序列;

ARIMA模型处理的时间序列都是平稳过程的，如果分析的序列不是平稳的，那要让其平稳，一般来说较为常用的就是对不平稳的原始时间序列进行差分运算，这样就会得到一个ARIMA（p，d，q）模型， 其中d表示差分的阶数。

（二）预测结果及其分析

本文在进行股票价格指数ARIMA模型预测的时候，将所有观测值同样分为8：2，并进行划分训练集和测试集。训练集共5742个观测，测试集1436个观测。选用SPSS软件操作，具体步骤如下：

1. 导入日期和收盘价两列训练集数据。

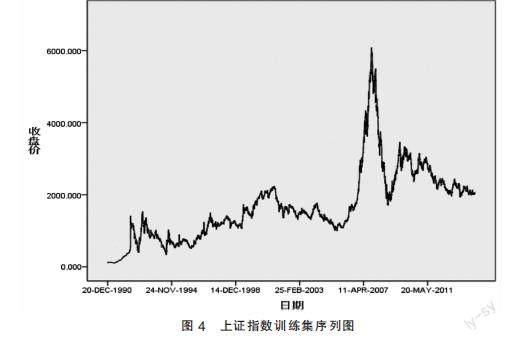
2. 排除季节成分影响。对训练集绘制序列图，如图4所示，所得结果可以看出该数据中不含有明显的季节成分，所以没必要做季节的分解。

3. 判断是否平稳。在用ARIMA分析时，需要保证序列是平稳的，因此需要对数据进行平稳性分析。根据序列自相关图（图5）和偏自相关图（图6）进行分析序列的平稳性。从中可以看出，序列自相关和偏自相关图都是拖尾的。说明序列是非平稳的。对于非平稳序列，通过差分进一步分析。

4. 一阶差分d=1，判断平稳性。从图7中可以看出，差分序列基本上均匀地排列在0刻度线上下。

同时做一阶差分后的自相关图（图8）和偏自相关图（图9），也可以判断序列是平稳状态的，可以进行后续分析。

5. 确定ARIMA模型中p、q值。经过反复试验，以AIC准则数值最小的原则，当p=1，d=1，q=1时，AIC的值为10.131，确定模型为ARIMA（1，1，1）。

6. 建立ARIMA（1，1，1）模型，同时对训练集进行拟合，图10中，UCL指预测上限，LCL指预测下限。从中可以看出，拟合程度较好。同时，ARIMA模型的参数结果见表1。

根据参数值，可以确定模型的表达式为

ΔX■=X■-X■ΔX■=22.735-0.917（ΔX■-22.735）+ε-0.932ε■（4）

接下来，将表达式应用到剩余1436个测试集身上，求出拟合值。并将原始观测值和拟合值对比，计算得出均方根误差RMSE=1396.527。

四、长短期记忆网络（LSTM）模型对股票价格走势预测

（一）理论介绍

长短期记忆网络（LSTM）模型是在循环神经网络（RNN）的基础上扩展出来的。RNN由于其记忆的短期性，不能解决长输入序列的信息传递问题，内部构造比较简单，所需的计算资源比LSTM少很多。图11表示LSTM的一个cell，从图中看出，核心为cell的状态和控制门，可以保留有用的信息在cell中，移除无用的信息。

Sigmoid函数：sigmoid层的输出约束在0～1之间。目的是幫助保留信息或者移除信息。假如为0，意味着不让任何东西通过，即移除;反之，若为1则意味着通过，所以保留;中间数，根据数值大小能体现数据的重要性。

Tanh 函数：主要是用来调节流经网络的值，将值约束在[-1，1]之间。

遗忘门：LSTM的第一步决定从单元中状态中抛弃什么信息。由遗忘门完成。该门会读取前一个隐藏状态和当前输入，输出一组对应前一个单元状态中数字 的[0，1]之间的权值，0是完全遗忘，1则代表完全保留。

输入门：LSTM接下来是确定被存放在单元状态中的是怎样的新信息。由输入门完成。先是隐藏状态和当前输入传输给Sigmoid函数，由该函数计算出哪些值更为重要。与此同时也把上面的值传递给tanh函数，把向量的值约束在-1～1之间，防止数值过大。然后与Sigmoid门输出值相乘，从而输出最终的值。

cell 状态：第一步先将之前的隐藏状态和遗忘门输出的向量进行点乘。接着将前面的输出和输入门的输出点乘，这样一来，输出的就是更新后的单元状态。

输出门：它决定了下一个隐藏状态。上面是单元状态，下面是隐藏状态。有关先前输入的信息都包含在隐藏状态中，基于此，神经网络才具备预测能力。

（二）预测结果及其分析

根据长短期记忆模型（LSTM）对上证指数进行拟合，拟合结果如图12所示。从中可以看出，测试集拟合程度较高，对比移动平均和自回归综合移动平均两种算法来说，当前LSTM算法是最优的。对于RMSE均方根误差的计算值近似为67.142，也是偏离程度最小的。

五、结论及建议

本文从简单模型开始，然后转向高级模型，通过对比移动平局、自回归综合移动平均、长短期记忆网络三种算法模型的结果，在三种预测模型中，长短期记忆模型（LSTM）相比较其他两种模型能更准确地实现短期股票的预测，当然，预测股票价格走势仅依靠收盘价是远远不够的，针对本文的模型预测总结出以下几点不足。

第一，移动平均法未考虑权重的影响。一次移动平均是假设每一期的数据在移动平均值中的作用是相等的，因此对每期数据赋予的权重是相等的，但实际上每一期的数据都包含着不同的数据信息量，近期的数据包含的信息可能比远期数据要多，但是在实际计算中并没有将这方面因素考虑进去的，没有对不同期的数据按照其包含信息量的不同对其赋予不同的权重。

第二，移动平均法未对步长的选取进行试算。通常来说，在使用移动平均法进行预测时，既希望模型的平滑能力要尽可能强，进而可以更好地抵消各种因素的干扰，显示出规律性，同时又希望预测值能够灵敏地反映出数据变化，以便于预测值不要滞后太多，但这两者不能同时兼顾到，因为要使预测值能很快跟上数据的变化，就必然要带进更多的随机误差。

通常情况下，N在时间序列的变化趋势比较稳定时，取值适合大一些，反之，在有明显变化及其波动时，N的选取宜小一些，有时常常会使用试算法，来确定合适的N，在本次预测中选取了测试集的容量为步长进行移动平均，对步长的选取并没有进行试算。

第三，ARIMA模型对长期预测效果不好。ARIMA模型在对许多时间序列都适用，其优点在于模型简单无需借助其他外生变量，缺点是对短期预测效果较好，但随着时间的延长其预测误差就比较大了。本次测试集含有1436个数据集，年限跨度从2014年6月13日至2020年4月30日，时间跨度比较长。

第四，影响价格走势因素考虑比较单一。影响股票价格走势的因素有很多，宏观、公司、行业和区域均是影响股票价格走势的因素，虽然目前来看LSTM算法是相对来说最优的，但是这一预测并不能足以确定股票是上涨还是下跌的。因为股价受到公司新闻和其他因素的影响，如公司的非货币化、合并或者拆分，还有一些无形的因素往往是无法实现预测的。

参考文献：

[1]张桂喜，马立平.预测与决策概论（第三版）[M].北京：首都经济贸易大学出版社，2013：42-45.

[2]CUI Yujie;XI Qipu;HAO Junzhang.Analysis of Shanghai Composite Index Variation Based on Regression Analysis[J].Higher Education of Social Science，2014（12）：118-122.

[3]许舒雅，梁晓莹.基于ARIMA-GARCH模型的股票价格预测研究[J].河南教育学院学报（自然科学版），2019，28（04）：20-24.

[4]白营闪.基于ARIMA模型对上证指数的预测[J].科学技术与工程，2009，9（16）：4885-4887.

[5]黄子建，刘媛华.长短期记忆模型在股票价格趋势预测应用研究[J].财政与金融，2020（01）：36-38.

*本文受北京市属高校基本科研业务费（No.110052971921/103）和北京市教委基本科研业务费（No.KM202010009013）资助。

（作者单位：北方工业大学理学院）