基于卷积神经网络的多车桥梁动态称重算法
邓露 罗鑫 凌天洋 何维

摘要:为识别多车工况下车辆过桥时的车辆重量,采用卷积神经网络技术开发出可用于多车轴重识别的桥梁动态称重(BWIM)算法.首先,利用车桥耦合系统采集不同车辆过桥时梁底的应变信号;之后,基于深度学习开源框架 KERAS搭建了包含9层卷积层、2层全连接层的卷积神经网络(CNN)模型,利用 Adam优化器训练 CNN模型以拟合所获得的应变信号与车辆轴重在不同工况下的变化规律,并最小化拟合误差;最后,对所开发的算法在单车和多车加载工况下的轴重识别精度进行了对比分析.结果表明:所提出的算法在单车和多车工况下的轴重识别误差均值基本低于5%,并且识别精度对车辆速度和横向位置的变化不敏感,说明算法的轴重识别效果良好且稳定.该多车 BWIM 算法摆脱了对桥梁影响线的依赖,为不适用于利用影响线方法进行动态称重的桥梁提供了可替代的称重技术.
关键词:桥梁动态称重;卷积神经网络;多车轴重识别;有限元分析
中图分类号:U446.2 文献标志码:A
Bridge Weigh-in-motion Algorithm Considering Multi-vehicle Based on Convolutional Neural Network
DENG Lu?,LUO Xin,LING Tianyang,HE Wei
(College of Civil Engineering,Hunan University,Changsha 410082,China)
Abstract:In this study, a new bridge weigh-in-motion (BWIM) algorithm based on the convolutional neural net? work technology was developed for identifying the axle weights of multi-vehicles crossing the bridge. First of all, the bridge strains under vehicular loading with variable weight were simulated using the vehicle-bridge coupling simula ? tion system. Then, a convolutional neural network, consisted of nine convolutional layers and two fully connected lay ? ers, was developed based on an open source framework for deep learning, i.e., KERAS. The convolutional neural net? work was trained by Adam optimizer to map the relationship between the bridge strain and the vehicle weight under different scenarios, and optimized by minimizing the fitting error. Eventually, the identification accuracy of the pro ? posed BWIM system was analyzed under the conditions of single- and multi-vehicle loadings. The results show that the mean identifying error of the proposed BWIM was less than 5% for both the single- and multi-vehicle scenarios, and changed slightly with the varying traveling speeds and lateral loading positions, indicating the good and stable performance of the proposed BWIM algorithm in axle weight identification. In addition, the proposed BWIM system doesn'tneed a bridge influence line in advance to identify the axle weight, and therefore provides an alternative technology for bridges that are not suitable for the influence line method.
Key words:bridge weigh-in-motion;convolutional neural network;axle weight identification for multiple vehicles;finite element analysis
桥梁动态称重技术克服了静态称重技术识别效率低的缺点,因其具有无需中断交通即可快速识别通行车辆重量信息的优点而广泛应用于实际交通工程中.其概念由 Moses[1]于1979年首次提出,主要根据桥梁特定位置的应变信息来反算桥上移动荷载的重量,也称为 Moses算法.之后众多学者对桥梁动态称重进行了深入研究.赵华等人[2]利用小波变换放大了车辆经过传感器时信号中的非连续变化斜率,进而求解车辆的轴数、轴距和速度.邓露等人[3]对比了经典的 BWIM 方法(Moses 算法和应变面积法)在不同中小跨径桥梁上的车重识别效果,对比结果表明桥梁跨径越小,轴重识别效果越佳.不过,Moses算法及其改进算法中并没有考虑车辆横向加载位置的影响,因此进行多车过桥工况下的车重识别时误差可能过大[4].对此,Quilligan[5]将影响面的概念引入 BWIM 中以考虑车辆横向加载位置对轴重识别精度的影响.Zhao 等人[6]分析了车轮荷载在不同梁上的横向分布特性并据此在 BWIM 中考虑了桥梁空间特性.宫亚峰等人[7]采用桥梁横向动力响应线和桥梁弯矩影响面方法考虑 BWIM 中的横向多车问题.但上述方法的实现都依赖桥梁影响面的标定或桥梁横向动力特性的获取,不仅实现难度大,技术要求高且识别精度受限于影响面的标定精度.且文献[8]指出在部分跨度较大的桥梁上可能并不适用使用影响线方法计算轴重,这些对 BWIM 在实际工程的应用造成了困难.
近年来,有学者尝试将人工神经网络(ANN)应用于 BWIM 中,如Gonza′lez等人[9]采用 ANN对 BWIM 系统的信号进行降噪和滤波.之后,Kim 等人[8]提出了一种利用桥梁主梁上应变信号的峰值通过神经网络识别车辆轴重的方法,但仅将应变峰值数据输入神经网络的做法忽略了应变信号中丰富的和车辆参数相关的信息[10].Kawakatsu等人[10-11]利用卷积神经网络(CNN)对传感器的信号曲线进行分析以此获取车辆速度、轴数和轴重等信息.Wu 等人[12]利用卷积神经网络通过信号重构的方法得到了车辆的轴数、速度和轴重.不过这些方法都未考虑多车过桥问题.
针对以上现状,本文提出了一种基于卷积神经网络实现多车轴重识别的 BWIM 算法.该算法将桥梁在不同横向位置和速度的多车加载下的响应信号和相应的车辆轴重信息对卷积神经网络进行训练,使其直接拟合桥梁响应和车辆轴重之间的复杂函数关系,从而避免了耗时的影响面标定以及对桥梁响应和车辆轴重之间的复杂的公式求解工作.本文首先建立了典型的 T 梁桥有限元模型,并采用了具有不同轴距、不同重量、不同车辆轴数的车辆模型;之后,利用车桥耦合系统来获取桥梁在不同多车加载工况下的响应信号,并以此对卷积神经网络进行训练,使其拟合桥梁响应信号与车辆轴重之间的关系并最小化拟合误差;最后,讨论了不同横向位置、车辆速度以及横向车辆数量对多车轴重识别精度的影响.
1多车称重卷积神经网络算法
神经网络是当前受到广泛应用的数据拟合工具,主要包括人工神经网络(ANN)、卷积神经网络( CNN)和循环神经网络(RNN)3种形式.在高频信号处理、高分辨图片处理等问题上,在搭建相似规模网络的情况下,CNN所需的权重参数数量远低于 ANN,因此也更易于训练[13].而 ANN则可能因为权重参数数据量过大出现模型难以训练的现象.RNN适用于处理前后具有关联性的序列数据,其各步的输出数据之间通常也具有一定的联系,典型应用如语句翻译[14-15].然而,车辆各个轴重之间、不同车辆的重量之间通常不具有明显的相关性.实际上,如式(1)所示,通过车辆轴重 P( x )和影响线 I( x )卷积的结果以及误差函数ε( x )可计算出桥梁的实测弯矩 M( x ),而桥梁动态称重的目的是通过桥梁的实测弯矩 M( x )及其他条件求得车辆的轴重 P( x ),因此桥梁动态称重为反卷积求解问题,故利用卷积神经网络(CNN)求解该反卷积问题可能会有较好的效果.如文献[16]使用基于 CNN 的反卷积方法通过超声波信号估计信号反射源的位置和该处反射超声波的振幅大小. Kawakatsu等人[10]也利用 CNN 方法,从桥梁响应中获得了单车工况下车辆的速度和轴重等信息.本文也拟采用 CNN 来求解多车过桥时的荷载识别问题.
桥梁动态称重理論中一般假定桥梁处于线弹性状态,则桥梁的弯矩和加载车辆的关系如式(1)所示:
式中:M ( x )代表实测弯矩;P ( x )代表车辆轴重函数;ε( x )代表理论弯矩(轴重 P( x )和桥梁影响线 I( x )的卷积)与实际弯矩 M( x )之间的误差.
由式(1)可知当已知桥梁的影响线和车辆轴重向量及车速、轴距等信息时能够得到车辆的实测弯矩,而已知桥梁实测弯矩来解算出行驶车辆的轴重、车速和轴距从理论上来说是可行的[10].根据实测弯矩响应的信号长度能够获得车辆过桥时间,从而获得车辆速度;不同轴距的车辆在桥上行驶时桥梁响应的特征不同,文献[17]也介绍了从实测弯矩中得到车辆轴距的算法;通过将不同横向位置的应变信号加入神经网络的训练集可以使卷积神经网络“学习”到不同横向位置对求解轴重的影响.因此桥梁响应中已包含了足够的求解车辆轴重的信息,且卷积神经网络在信号特征提取和回归拟合方面都表现出了突出的拟合效果和广泛的应用前景,故可以通过卷积神经网络直接拟合桥梁响应和多车车辆轴重之间的关系实现轴重预测,同时还能最小化误差对轴重求解的影响.至于单车工况,则可视为其它所有车道上车辆轴重均为零的“特殊”多车工况.
本研究提出的卷积神经网络模型主要包含输入层、卷积层、池化层、全连接层以及输出层,其基本架构如图1所示.一个测点在输入层中的输入数据格式为4000×1的向量,即时长4 s、采样频率为1 kHz 的应变信号;卷积层主要用于提取输入数据中和车辆参数相关的特征,其中卷积核的大小如表1所示,步长为1.由于本文每条输入数据中皆有部分信号值为负,故激活函数采用在“Relu”激活函数的基础上扩展了负区间的“Leaky Relu”激活函数,以使神经网络在正负区间下都取得较好的非线性拟合能力.“Leaky Relu”激活函数表达式为 y = max(αx,x ),本文中α=0.3;每层卷积层后面接一层池化层,池化层的作用主要为在保留信号特征的基础上降低卷积层的大小,本研究中池化层都采用最大值池化方法,池化层参数设置如表1所示;卷积神经网络最后几层为全连接层,用于拟合输入信号经过卷积核池化后特征矩阵与轴重之间的复杂关系,其结构与一般神经网络类似.
本文的卷积神经网络模型将一个车道上的输出变量数目设置为5个,每一个输出代表一个轴重.对本文采用的2轴车和3轴车,其轴数不足5轴,则相应位置的输出值以零补齐.本文采用的桥梁模型具有两个车道,故卷积神经网络模型输出变量数目共10个,因此神经网络的输出数据格式为10×1.进行预测前需要使用卷积神经网络预先获知车辆轴数(使用额外的车轴探测传感器).对于轴数为 n 的车辆来说,只需取卷积神经网络输出向量的前 n 项作为车辆轴重识别结果而无需关注其它项.
由于本文的问题属于神经网络中的非线性拟合问题,故神经网络的损失函数采用在神经网络非线性拟合问题中受到广泛使用的均方差(MSE )损失函数,其表达式如式(2)所示:
式中:N 为神经网络输出数据的个数10;yi为输出数据的真实值;i为神经网络的预测值.
本文采用 Adam 优化器[18]作为该卷积神经网络模型的权重参数优化器,该优化器可以动态且平稳地调整每个参数的学习率,已被广泛应用于各类经典的神经网络模型的模型中.
图1中卷积过程“7×1×16-s-1”中的“7×1×16”代表使用16个7×1的卷积核,“s-1”代表卷积核步长为1.最大值池化过程下“2×1-s-2”代表使用2×1的核以步长2进行最大值池化操作.
卷积神经网络的参数除了权重参数外,还包括神经网络的层数、卷积核大小和全连接层数等超参数.和权重参数不同,卷积神经网络的超参数目前大多需要人为定义.
本文参考文献[10]和实际识别误差情况得到基于本文训练数据集的最优的神经网络的超参数如表1所示.在此超参数基础上增加卷积层层数或全连接层层数均未发现明显的识别精度增长,而减少层数则会使识别精度降低.
2数值模拟
2.1桥梁模型
本研究选取了一座有代表性的简支 T 梁桥进行数值模拟.该桥梁跨径为20 m,桥面宽8.5 m,双车道设计,具有4片 T 梁,每片梁高1.5 m.混凝土的弹性模量为3.45×104 MPa,泊松比为0.2,密度为2653 kg/m3,其横截面如图2所示.
此外,本文使用有限元分析软件 ANSYS 建立了该桥的有限元模型.桥梁的支承方式为两端简支,桥面板和主梁均采用 Solid185单元模拟.桥梁纵向单元长度为0.4 m,横向单元长度为0.3 m,有限元模型图如图3所示.
本研究使用车桥耦合数值仿真方法求解车辆过桥响应.该方法主要利用Newmark-β法求解模态坐标下的动力学方程得到桥梁的响应,具体求解过程见文献[19-20].由该方法计算结果与实桥数据的对比可知,该桥耦合数值仿真方法是准确可靠的,且该桥梁模型在文献[21]中同样用于获取桥梁梁底的应变响应.
在模拟车辆过桥路线时按均匀分布随机选取车辆过桥时车辆中心的横向位置,其中车道1和车道2的车辆中心横向位置范围分别由图2中的 P1-P2和 P3-P4确定.本文参考文献[7]和[16]的做法分别在桥梁跨中每片梁梁底选取一个点作为应变提取点,记为 A、B、C、D,如图3所示.
2.2 车辆模型
本研究选取具有不同车辆参数的2轴车、3轴车和5轴车模型作为加载车辆,车辆的总重在范围10~60 t 内按均匀分布选取,车辆的轴组之间的距离范围设置为2.1~4.4 m[22],车辆轴组内部的轮距范围设置为1.02~1.85 m[22],车辆速度在10~30 m/s 内随机选取.典型的2、3和5轴车的模型分别如图4中(a)(b)和(c)所示.需要注意的是,各模型的背面图均如图4(d)所示.各模型的详细参数参见文献[23-26].
2.3获取训练、测试和验证数据
为了模拟不同车辆过桥情况,本文分别选用了1000辆2、3和5轴车模型.在模拟单车过桥的工况时,每次首先选定模型车辆的轴数,并在车速范围中随机选取一个车速,之后在图2所述 P1-P2和 P3- P4范围内随机选取车辆行驶路线的横向位置.在模拟多车过桥的工况时,两个车道上行驶的车辆轴数、横向加载位置以及行驶速度均在指定范围内随机选取,与单车工况下的选取准则相同.其中各车道上通行车辆的轴数情况如表2所示.
桥上道路的路面平整度根据我国《车辆振动输入路面平度表示方法》(GB/T 7031—1986)[27]来模拟,路面不平整度为规范中的“A”级.
由以往的研究可以发现,卷积神经网络技术应用于 BWIM 上时其训练数据量可能达到百万级[10],这可能会对卷积神经网络在 BWIM 上的应用造成困难,因此应用卷积神经网络技术时应当考虑训练数据量和精度的平衡.本文的训练数据量为15000组,即为上述工况组合得到的6000组单车过桥和9000组多车过桥数据.各工况的数据采样频率都为1 kHz,由最低行驶速度确定采样时间为4 s,采样时间不足4 s 造成的数据短缺可用零补齐.得到车辆过桥响应后将响应曲线的值归一化到(0,1)之间并加入50 dB 的高斯白噪声以模拟实际情况中的信号噪声.图5所示为在3轴车随机加载下未加白噪声处理的桥梁应变响应曲线.车辆各轴轴重同样归一化到(0,1)之间以降低梯度消失和梯度爆炸现象出现的可能性.
3 结果讨论
3.1卷积神经网络的训练
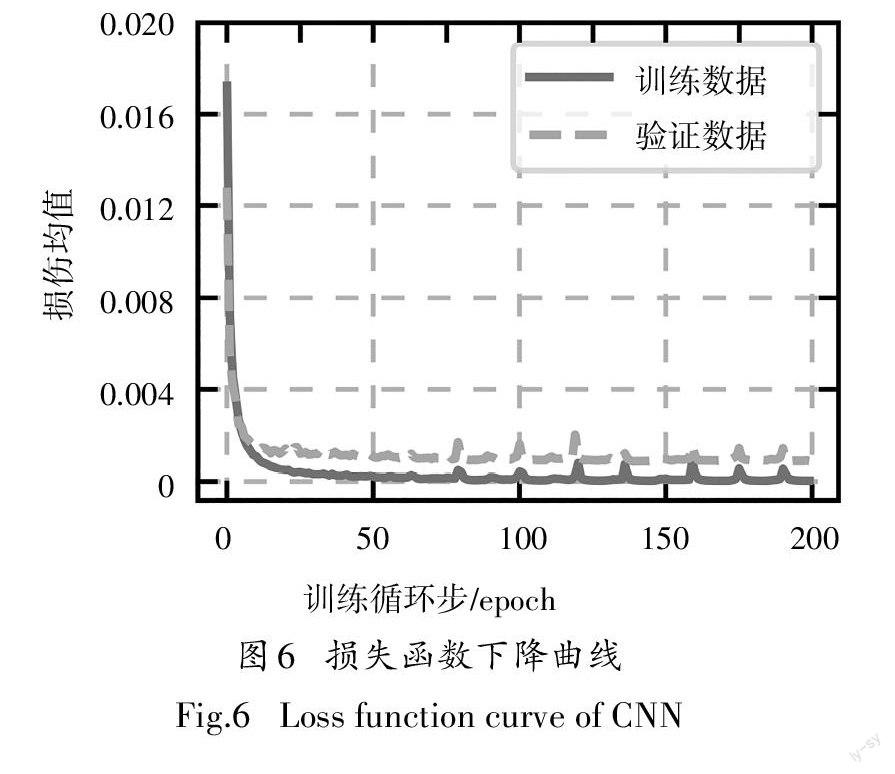
本文将按照2.3所述生成的15000组桥梁应变数据作为卷积神经网络的训练集,再生成1500组数据作为卷积神经网络的验证集.每个训练循环步(epoch)中训练样本数为64,图6展示了在200个训练循环步中损失均值的下降情况.
从图6中可以看出神经网络的权重参数初始化后训练数据的损伤均值比验证数据损伤均值低,随后训练数据的损伤迅速下降.在第15训练循环步时的训练数据损失低于验证数据损失,说明此时卷积神经网络有过拟合现象,到第200训练循环步时卷积神经网络训练数据损伤均值低于1×10-4.本文取訓练到200训练循环步的卷积神经网络模型作为最终预测车辆轴重的神经网络模型.
在训练过程中,卷积神经网络各个权重参数的学习率和步长皆由 Adam 优化器根据各参数梯度的一阶矩估计和二阶矩估计动态调整,使得神经网络能够平稳有效地接近最优解.卷积神经网络的超参数则根据实际效果手动调整,调整后得到的基于本文训练数据集的最优超参数如表1所示.
3.2 单车车重识别
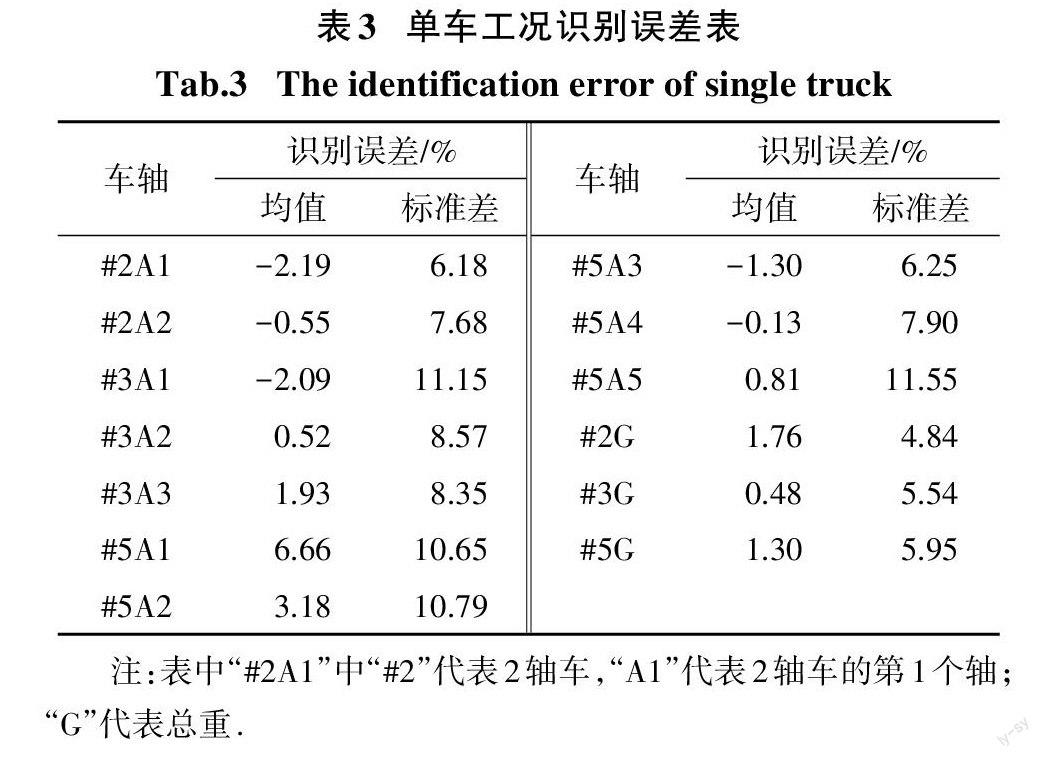
为了探究本文所采用的卷积神经网络模型对单车工况的轴重预测精度,本文在训练数据之外按2.2节的车辆参数生成了50组2轴车、3轴车和5轴车模型.由于实际情况中车辆主要沿着车道中心线行驶,故车辆行驶的横向位置设为车道1中心,行驶速度设为20 m/s.将按上述条件得到车辆行驶时桥梁4片子梁 A、B、C、D 处的应变响应输入到训练好的卷积神经网络模型中得到各个预测轴重,其中预测轴重的误差均值和标准差如表3所示.
由表3可以看出,2轴车的轴重识别误差均值绝对值在3%以下,标准差在8%以下;3轴车的轴重识别误差均值绝对值也在3%以下,标准差基本在12%以下;5轴车轴重识别误差均值绝对值基本在7%以下,标准差基本在12%以下.识别结果2轴车优于3轴车,3轴车优于5轴车,说明轴数越多识别效果略有降低但仍能满足实际工程的需要.三种车总重误差均值绝对值都低于2%,误差标准差也低于6%,说明卷积神经网络对车辆总重的识别效果比轴重识别效果更好.本研究单车工况的总重比文献[7]中使用神经网络的单车 BWIM 算法精度略高,但二者误差均值均接近1%,标准差均接近5%,说明本研究提出的算法在单车工况下实现了较高的识别精度.
3.3 多车车重识别
为了探究卷积神经网络模型在不同多车过桥工况下的轴重识别精度,本文考虑了相同横向加载位置下以不同车速过桥和相同车速下以不同横向位置加载的工况,并且选用训练数据之外的2轴、3轴和5轴车各50辆用于模拟变化的加载车型.
3.3.1 不同横向位置工况
在探究由于两车道上的车辆的横向加载位置变化对卷积神经网络模型预测精度的影响时,为便于研究,本文重点研究两车道上车辆的相对间隔的变化,即控制某一车道上的加载车辆沿道路中心行驶,另一车道上的车辆沿着不同横向位置的加载路线过桥.具体而言,由于两车道沿桥梁纵向成对称分布,且通常情况下在慢车道(即本文中的车道2)行驶的车辆占据多数,因此,本文主要假定车道1上的车辆一直沿车道中心线加载,而车道2上车辆行驶的横向位置则在图2中 P3-P4之间按0.5 m 的间隔选取5个横向位置,其中两车道上的加载车辆模型的轴数情况如表4所示.
对于表4中展示的加载车辆组合类型,每个类型中车辆模型横向位置会变化5次,每次变化均对应50个不同的车辆模型加载,故最终共得到1500组桥梁应变响应.由桥梁响应和卷积神经网络得到各个轴预测轴重误差的均值和标准差如图7和图8所示,车辆位置的坐标轴如图2所示,路面最左侧为坐标原点.本文以 x 坐标值来表示车辆横向位置.
图例“Z1#2”中,“Z1”表示表4中车辆组合类型的组合1,“#2”表示2轴车,如在图7(a)中“Z1#2”表示组合1下2轴车所有轴重整体的误差均值,其余图例的含义以此类推.
从图7和图8中可以发现车道1的均值和方差离散性较车道2更好,且车道1中各轴的误差标准差集中在15%左右,误差均值集中在5%左右,说明对于车辆加载路线沿车道中心加载时预测效果较好,而某一车辆偏离车道中心线加载虽会降低其自身的识别精度,但不影响其他车道上沿中心线加载的车辆的轴重识别精度.另外,从图中可以发现该模型对2轴车模型的轴重识别精度最高,其次为3轴车,最后是5轴车,这是由于5轴车的后三个轴的间距较小使得相应轴在应变信号中的特征不明显所造成的.不过从图中可以发现该卷积神经网络模型对多车轴重的识别误差均值基本在±5%左右,误差标准差大部分在15%左右,说明卷积神经网络对不同横向位置的多车问题实现了良好的识别效果.
本文继续研究了车道2上的车辆轴数与加载位置变换对神经网络识别车辆总重的精度影响,结果如表5所示.从表5中可知,当车辆相对加载位置变换时,各个工况下车道2上的车辆加载位置越靠近车道中心,对应表中位置6.45 m 和6.95 m,两车道上车辆的总重识别误差均值越趋近于零,结合实际情况中车辆一般行驶在车道中央来看,这是有利于卷积神经网络模型在实际情况中的使用.
另外,表5中每个工况中车辆加载位置为5.45 m 时模型对车道上车辆的总重识别误差均较大,这是由于当车道2车辆沿该路线加载时与车道1上的车辆相隔较近而导致应变信号互相干扰的程度较大所导致的.在实际工程中,为安全起见,驾驶员可能并不会近距离相隔行驶.总体而言,该卷积神经网络在多数常见加载路线下对车辆总重具有优秀且稳定的识别精度,误差均值基本低于5%.
3.3.2 不同速度工况
在研究不同车速对 BWIM 算法的识别精度影响时,令慢车道(车道2)上行驶的车辆速度为10、15、20、25、30 m/s 5种情况,同时设定快车道(车道1)上行驶的车辆速度比车道2上的快5 m/s.车辆在各自车道行驶时其横向加载位置分别为该车道中心.对于任意一种车速,都按表4中6种车辆组合类型分别行驶.按2.2节的车辆参数生成50个相应的车辆模型进行加载以获得不同速度下多车过桥的桥梁应变响应.将所获得的桥梁应变响应输入到卷积神经网络中得到预测轴重的误差均值和标准差如图9和图10所示.
从图9和图10中可以看出不同速度下,车道1和车道2的2轴车和3轴车的识别效果要优于5轴车,且2轴车和3轴车在不同速度下的误差均值和误差标准差曲线较为平滑,误差均值集中在0%左右,误差标准差集中在15%左右,说明卷积神经网络对不同速度的2轴车和3轴车的轴重都具有良好的识别效果.
车道1中车辆在35 m/s 时误差均值绝对值和误差标准差有增大现象,但大部分曲线增大幅度不大,且部分曲线保持平稳,如图9(a)中的2軸车(Z1#2)和2轴车(Z4#2),这是由于速度35 m/s 的工况并没有在训练数据中出现过导致的误差增大现象,但误差增大的幅度不大和部分曲线保持平稳说明了卷积神经网络仍具有较好的泛化能力.
对比不同速度下车道1中“Z1#2”、“Z4#2”和“Z5#2”车辆组合类型下2轴车和不同横向位置下相同车辆组合类型的2轴车可以发现,不同速度下车道1该3种车辆组合类型的2轴车均值和标准差曲线更加接近,说明不同速度对卷积神经网络识别稳定性的影响更低.
同时本文还探究了不同速度对神经网络识别车辆总重精度的影响,如表6所示.从表6中可知,随着速度的减小,车辆总重误差均值绝对值呈减少的趋势,部分数据如车道2的5轴车“Z3#5”工况的总重误差均值绝对值虽然略有增大,但其标准差呈减小的趋势,综合而言识别效果更佳.故随着车辆速度的减小,车辆总重的识别效果更好,且实际中汽车通常以偏低速度行驶,这有利于算法在实际情况中的应用.
4 结论
本文基于卷积神经网络提出一种无需预知车辆轴距、速度等信息和进行影响面标定即可实现多车轴重识别的 BWIM 算法,并分析了车辆以不同行驶速度沿着不同加载路线过桥时该算法的轴重识别精度,得到以下结论:
1)在进行单车和多车轴重识别时,该算法对2、3轴车的识别精度高且识别效果稳定,而对5轴车的识别精度略低,这可能与本文所采用的5轴车的第3、第4和第5轴的间距较小有关.
2)研究发现随着加载车辆的横向间距增大,应变信号间的干扰程度会降低,该 BWIM 算法对车辆轴重和总重的识别效果越好.
3)本文所提出的 BWIM 算法在多车过桥工况下误差均值仍低于5%,且识别精度受车辆行驶速度与车道加载位置的影响很小,说明其具备良好且稳定的识别效果.
4)该算法使用前无需预先获取车辆速度、车辆轴距和桥梁影响面等信息,减少了 BWIM 系统所需传感器数量,提高了桥梁动态称重的实用性.同时也为不适用于利用影响线方法进行动态称重的桥梁提供了可替代的称重技术.
尽管本文提出的算法具有无需进行影响面标定、所需传感器数量少等优点,但仍存在以下不足:
1)本文的训练数据量较大.作者在接下来的研究中将考虑引入迁移学习等技术进一步缩减所需训练数据量的大小.
2)利用 CNN 处理信号从而获取车辆轴数的方法同样具有较大研究价值.作者在后续研究中将对此进行深入探索.
参考文献
[1] MOSES F. Weigh-in-motion system using instrumented bridges[J]. Transportation Engineering Journal of ASCE,1979,105(3):233-249.
[2] 赵华,谭承君,张龙威,等.基于小波变换的桥梁动态称重系统车轴高精度识别研究[J].湖南大学学报(自然科学版),2016,43(7):111-119.
ZHAO H,TAN C J,ZHANG L W,et al. Improved identification of vehicular axles in BWIM system based on wavelet transform[J]. Journal of Hunan University(Natural Sciences),2016,43(7):111-119.(In Chinese)
[3] 邓露,李树征,淡丹辉,等.桥梁动态称重技术在中小跨径混凝土梁桥上的适用性研究[J].湖南大学学报(自然科学版),2020,47(3):89-96.
DENG L,LI S Z,DAN D H ,et al. Study on applicability of bridge weigh-in-motion technology in short-to medium-span con ? crete girder bridges[J]. Journal of Hunan University(Natural Sci? ences),2020,47(3):89-96.(In Chinese)
[4] DEMPSEY A,JACOB B,CARRACILLI J. Development and experimental testing of orthotropic bridge weigh-in-motion for deter? mining axle and gross vehicle weights [ C]// Wave Symposium, Weigh-in-motion of Road Vehicles. Paris:Transportation Re? search Board,1999:227-238.
[5] QUILLIGAN M. Bridge weigh-in-mtion:development of a 2-Dmulti-vehicle algorithm [J]. Trita BKN Bulletin , 2003, 69:A-144.
[6] ZHAO H,UDDIN N,O′BRIEN E J,et al. Identification of vehicular axle weights with a bridge weigh-in-motion system considering transverse distribution of wheel loads[J]. Journal of Bridge Engi? neering,2014,19(3):04013008.
[7] 宫亚峰,宋加祥,谭国金,等.多车桥梁动态称重算法[J].吉林大学学报(工学版),2021,51(2):583-596.
GONG Y F,SONG J X,TAN G J,et al. Multi-vehicle bridge weigh-in-motion algorithm[J]. Journal of Jilin University (Engi? neering and Technology Edition),2021,51(2):583-596.( In Chinese)
[8] KIM S,LEE J,PARK M S,et al. Vehicle signal analysis using artificial neural networks for a bridge weigh-in-motion system[J]. IEEE Sensors Journal,2009,9(10):7943-7956.
[9] GONZ?LEZ A,PAPAGIANNAKIS A T,O′BRIEN E J. Evaluation of an artificial neural network technique applied to multiple- sensor weigh-in-motion systems[J]. Journal of the Transporta? tion Research Board,2003,1855(1):151-159.
[10] KAWAKATSU T,AIHARA K,TAKASU A,et al. Deep sensingapproach to single-sensor vehicle weighing system on bridges[J]. IEEE Sensors Journal,2019,19(1):243-256.
[11] KAWAKATSU T,AIHARA K,TAKASU A,et al. Fully-neuralapproach to heavy vehicle detection on bridges using a single strain sensor[ C]//2020 IEEE International Conference on Acous ? tics,Speech and Signal Processing. Barcelona: IEEE,2020:3047-3051.
[12] WU Y,DENG L,HE W. BwimNet:a novel method for identifying moving vehicles utilizing a modified encoder-decoder architec ? ture[J]. Sensors,2020,20(24):7170-7193.
[13] KRIZHEVSKY A,SUTSKEVER I,HINTON G E. ImageNet classification with deep convolutional neural networks[J].Communi? cations of the ACM,2017,60(6):84-90.
[14] HOCHREITER S,SCHMIDHUBER J. Long short-term memory[J]. Neural Computation,1997,9(8):1735-1780.
[15] CHO K,VAN M B,GULCEHRE C,et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[ C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. Doha:Association for Computational Linguistics,2014:1724-1734.
[16] CHAPON A,PEREIRA D,TOEWS M,et al. Deconvolution of ultrasonic signals using a convolutional neural network[J]. Ultrason? ics,2021,111:106312.
[17] HE W,LING T,O′BRIEN E J,et al. Virtual axle method forbridge weigh-in-motion systems requiring no axle detector [J]. Journal of Bridge Engineering,2019,24(9):04019086.
[18] KINGMA D,BA J. Adam:A method for stochastic optimization[ C]// Proceedings of the 3rd International Conference on Learning Representations , Conference Track Proceedings. San Diego:OpenReview,2014:1-15.
[19]何維.中小跨径梁桥动力冲击系数研究[D].长沙:湖南大学,2015:8-10.
HE W. Study of dynamic impact factor for medium and small span beam bridge[ D]. Changsha:Hunan University,2015:8-10.( In Chinese)
[20] DENG L,CAI C S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges[J]. Engineering Structures,2010,32(1):21-31.
[21] HE W,DENG L,SHI H,et al. Novel virtual simply supportedbeam method for detecting the speed and axles of moving vehicles on bridges [J]. Journal of Bridge Engineering ,2017,22(4):04016141.
[22] MIAO T J,CHAN T H T. Bridge live load models from WIM data[J]. Engineering Structures,2002,24(8):1071-1084.
[23] HARRIS N K, O′BRIEN E J, GONZ?LEZ A. Reduction ofbridge dynamic amplification through adjustment of vehicle sus ? pension damping[J]. Journal of Sound and Vibration,2007,302(3):471-485.
[24] SHI X M,CAI C S. Simulation of dynamic effects of vehicles onpavement using a 3D interaction model[J]. Journal of Transporta? tion Engineering,2009,135(10):736-744.
[25] ZHANG Y,CAI C S,SHI X,et al. Vehicle-induced dynamic performance of FRP versus concrete slab bridge[J]. Journal of Bridge Engineering,2006,11(4):410-419.
[26] ZHOU Y F,CHEN S R. Fully coupled driving safety analysis ofmoving traffic on long-span bridges subjected to crosswind[J]. Journal of Wind Engineering and Industrial Aerodynamics,2015,143(1):1-18.
[27]车辆振动输入-路面平度表示方法:GB/T 7031—1986[ S].北京:中国标准出版社,1986:2-5.
Vehicle vibration-describing method for road surface irregularity: GB/T 7031—1986[ S]. Beijing:Standards Press of China,1986:2-5.(In Chinese)

