基于ARMA模型的郑州市气温衍生品定价研究
王福宁
一、引言
天气衍生品是建立在温度、湿度、降水、风等天气变量上的金融合约。自1999年第一份温度期货合约在芝加哥商品交易所(CME)交易以来,天气衍生品已成为管理天气风险的最重要的金融工具。
气温衍生品是天气衍生品市场中最常见的一种类型,有一些文献[1,3]涉及气温建模,其中Alaton[1]引入了随月份变化波动率的Ornstein-Uhlenbeck (O-U)过程来模拟气温演化。Cao 和Wei[3]利用均值回归模型模拟气温,建立了基于气温的动态评估模型。由于天气衍生品市场是不完备的,所以经典的金融衍生品定价方法,如Black-Scholes公式并不适用。 因此,研究者们从不同角度提出了多种方法,如边际效用法[4]、指数建模[5]、均衡定价[6]、ARMA时间序列模型法[7-9]等。 Li Peng,Xiaoping Lu,Song-Ping Zhu[10]基于偏微分方程方法,利用效用无差异估值中提取的市场风险价格对天气衍生品进行定价。Li Peng[11]对两个典型过程的天气衍生品进行了定价:Ornstein–Uhlenbeck过程和带跳跃扩散的Ornstein–Uhlenbeck过程,并用单侧Crank–Nicolson格式,分别求解这两个过程对应的偏微分方程和积分微分方程。
本文拟在已有研究的基础上,采用ARMA时间序列模型对郑州市气温变化过程进行建模,并利用该模型进行氣温预测,最后检验模型的准确性。
二、 数据与研究方法
(一)数据来源与预处理
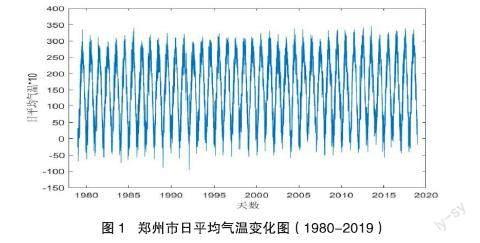
郑州是河南省的省会城市,是中国中部重要的交通枢纽和农业城市。从中国气象科学数据共享服务网收集了1980-2020年间的日平均气温数据,为了消除闰年的影响,剔除了所有闰年2月29日的日平均气温。因此,共有14965个观测值,没有缺失数据。利用郑州市40年(1980-2019年)的日平均气温数据来构建气温预测模型,并用预测模型预测郑州市2020年的日平均气温。
经过Matlab R2019a 软件处理,得到了40年的日平均气温的折线图,如图1所示。
(二)模型的建立
根据前文分析得出,郑州市日平均气温数据的变化过程具有很强的季节性变化,可以用一些正弦函数来模拟季节相关性,函数形式如下:
式中,t表示时间,以天为单位,为相位角,日平均气温的季节性变化呈现出以一年为单位的周期性,为了数据统一,删除闰年2月29日的气温数据,应取。因受到全球的温室效应,每年的气温以微弱的趋势增长,可以合理的假设这种微弱的变化是线性的,用Bt表示。因此,郑州市日平均气温变化过程可写为如下形式:
其中Tt为时间t的日平均气温,A、B、C以及是由历史日平均气温数据拟合的参数,Xt为去除趋势和季节性后的随机变量。
为便于参数估计,将(2)式作如下等式变换:
整理可得:
因为和是常数,所以可将(4)式看成是一个线性方程:
即:
三、模型的参数估计与结果分析
(一)ARMA模型的估计
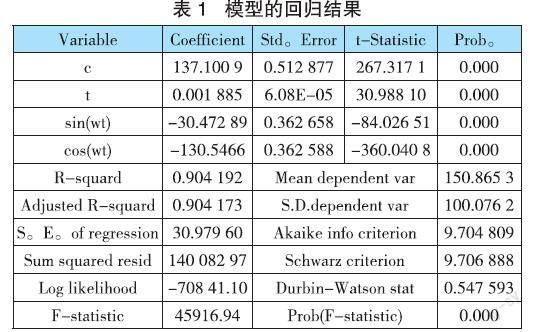
用Eviews 10软件对公式(5)进行参数估计,得到结果如表1所示。
由表1可知,各项变量系数都显著,但D-W值仅为0.547593,说明模型存在序列正相关性,需要对其进行修正。首先对随机变量进行单位根检验,结果见表2。由表2可知,ADF检验的统计量为-43.61932,明显小于在1%、5%、10%的显著性水平下的临界值,说明随机变量没有单位根,且序列平稳。其次,通过对随机变量绘制出自相关系数图和偏自相关系数图后,可以判断出它是一个平滑的非白噪声序列。因此,需要引入ARMA模型进行修正随机变量,发现引入ARMA(2,2)后,各项系数显著,D-W值为2.001 518,十分接近于2,说明模型不存在序列相关性,模型拟合的结果好,具体结果见表3。
(二)预测结果
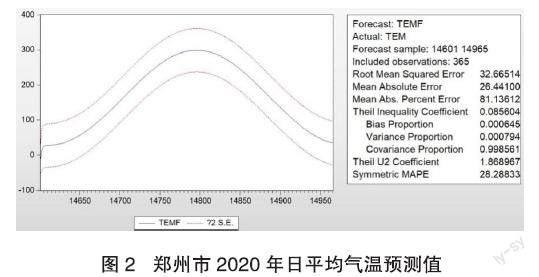
根据上述分析所得的时间序列ARMA模型,运用Eviews10软件对郑州市2020年的日平均气温进行预测,发现所构建的模型比较好,见图2。
本文通过计算偏差比率、方差比率和协方差比率进一步验证了模型的准确性,其三个比率值计算结果分别为0.000645,0.000794,0.998561。从这三个值中可看出偏差比率和方差比率的值较小,协方差比率值较大,且三个值和1,说明该模型预测较好。
四、 基于蒙特卡洛方法对气温衍生品定价
选取累积制冷指数(cooling degree days,CDDs)为研究对象,探讨气温的期货定价问题。 CDDs的表达式为:
其中是基准温度,基准温度一般是65华氏度或18 摄氏度,根据我国国情,选择。Ti是第i天的日平均气温。
假设期权的合约期限在T1和T2之间,且T2是合约的到期日,r为无风险利率,C为名义价值,S(T)为到期时标的资产的实际价格,F(t)为远期合约在时间t时的价值,原理上,当无风险利率为常数,期货合约和远期合约有相同的到期日和交割日时,其期货合约的价格等于远期合约的价格。即
这里的E为风险中性测度下的期望,我们假定风险市场价格为0。
选择CDDs期货合约为例,预期合约的终值为预期的CDDs值,即CDDs在时刻t的期货价值为:
根据上式(11)可知,是已知的,只需用蒙特卡洛方法计算。
选择2020.8.1-2020.8.31为合约期限,合约的名义价值C=100,即每点CDDs指数为100元,采用蒙特卡洛方法,计算出这一时期内CDDs值。当经过100000次模拟后,发现CDDs模拟值趋于稳定,达到仿真要求。
五、展望
我国的天气特征具有复杂性且受到多种因素的影响,天气的变化与各个行业以及我们的生活息息相关,如2021年河南7.20强降雨事件,给各个行业的发展和市民的生活带来了诸多影响,农业生产损失更是高达上亿元。因此开发出适应我国的天气衍生品用于应对天气风险具有一定的现实意义,而我国目前的天气衍生产品市场亟待完善,需要来自金融市场、法律甚至是媒体等多方共同努力来促进天气衍生品市场的蓬勃发展。
参考文献:
[1] Alaton, Djehiche and Stillberger.On Modelling and Pricing WeatherDerivatives.Applied Mathematical Finance,2002,9:1-20.
[2] Bhowan A.Temperature derivatives School of Computational and Applied Mathematics,University of Wiwatersrand.2003.
[3] Cao M.and Wei J.Weather derivatives valuation and market price of weather risk. Future Markets, 2005,24(11):1065-1089.
[4]M. Davis.Pricing weather derivatives by marginal value[J]. Quantitative Finance, 2001, 1(3): 305-308.
[5] Gregor Dorfleitner,Maximilian Wimmer. The pricing of temperature futures at the Chicago Mercantile Exchange[J].Journal of Banking and Finance, 2009,34(6):1360-1370.
[6] Yongheon Lee, Shmuel S. Oren. An equilibrium pricing model for weather derivatives in a multi-commodity setting[J]. Energy Economics, 2009, 31(5):702-713.
[7]郭建國,牛珊.基于ARMA模型的气温衍生品定价研究[J].商业经济,2015(10):40-41+69.
[8]曾小艳,陶建平.基于ARMA模型的气温衍生品定价研究:以武汉市为例[J].区域金融研究,2014(07):12-17.
[9] 李嫣然.天气金融衍生品定价研究—基于ARMA的时间序列模型[J].保险职业学院学报,2017,31(04):28-33.
[10] Li Peng, Xiaoping Lu, Song-Ping Zhu. Pricing weather derivatives with the market price of risk extracted from the utility indifference valuation, Computers and Mathematics with Applications, 2020,79: 3394C3409.
[11] Li Peng. The valuation of weather derivatives using one sided Crank-Nicolson schemes. Computational Economics,2020.
作者单位:华北水利水电大学数学与统计学院

