非饱和流固耦合物质点方法(CMPM的原理及应用
王斌 周傲 陆盟 王佳俊

摘 要:基于连续介质力学的质量及动量守恒原理,考虑了固-液两相材料的水力耦合相互作用,推导并提出了基于速度场(v-w formulation)的耦合物质点方法(CMPM),可考虑水力耦 合作用下,饱和/非饱和结构的大变形力学行为.同时,详细描述了耦合物质点方法的公式推导、矩阵离散过程以及数值实现步骤.随后,通过对比一维太沙基饱和土固结理论解,以及Liakopou-los非饱和砂土的入渗试验,初步验证了耦合物质点方法在水力耦合问题上的准确性.最后,结合 某边坡在降雨作用下的失稳破坏全过程,分别模拟了持续降雨以及短暂降雨作用下,边坡的深层破坏及浅层剥蚀现象,进一步验证了方法在岩土流固全耦合大变形问题中的适用性.
关键词:耦合物质点方法;控制方程;离散过程;数值实现;降雨滑坡
中图分类号:TU443 文献标志码:A
Formulations and Applications of Coupled Material Point Method for Unsaturated Soils
WANG Bin1?,ZHOU Ao1,2,LU Meng3,WANG Jiajun1,4
(1.State Key Laboratory of Geomechanics and Geotechnical Engineering,Chinese Academy of Sciences,Wuhan 430071,China;
2.School of Civil and Environmental Engineering,Hubei University of Technology,Wuhan 430068,China;
3.College of Civil Engineering,Tongji University,Shanghai 200092,China;
4.Faculty of Engineering,China University of Geosciences,Wuhan 430074,China)
Abstract:Based on the mass and momentum conservations of the continuum,this paper presents a novel coupled material point method based on the v-w formulation,which fully considers the large deformation mechanics of saturate and unsaturated structures under the interactions between the solids and the fluids.For simplicity,the gas phase is neglected in the formulation,while an additional item,i.e.degree of saturation,is incorporated in the gov-erning equations to simply study the saturated/unsaturated soils.The detailed derivation process of the governing equations,discretization process in the matrix forms and the computational cycles of CMPM is introduced.Via two benchmark examples,i.e.one-dimensional Terzaghi consolidation solution,and the Liakopoulos test,the validity ofthe CMPM is proven.In the end,a slope failure analysis due to the rainfall infiltration is presented,where both deep progressive and superficial slope failures are shown,further demonstrating that CMPM is a promising tool in simulat-ing hydro-mechanical problems.
Key words:coupled material point method(CMPM);governing equations;discretization process;numerical simulation;rainfall-induced slope failure
我國是滑坡灾害多发的国家,近年来,滑坡造成的年均死亡人数已连续多年超过1000人,滑坡灾害 不仅给当地居民的生命财产造成极大损失,有的还 严重影响铁路、公路、水运及水电站等基础设施的安全运营[1-4].降雨一直是诱发滑坡灾害的一个重要因 素,全国 290个县市地质灾害调查结果表明,滑坡在地质灾害中所占比例高达51%,而降雨诱发的滑坡比例竟达到滑坡总数的90%[5].因此,准确描述与预 测滑坡的运动过程及其致灾范围,对于滑坡灾害的防治具有重要的意义.
目前,对于滑坡运动过程的描述一般采用数值试验进行仿真模拟[6-7].传统的有限元方法因为在处理大变形时,容易造成网格的奇异,雅可比矩阵出现 负值,因此不能有效模拟坡体在产生初始破坏后的渐进大变形过程.相比之下,物质点方法(MPM)则 通过使用拉格朗日以及欧拉两套网格,避免了有限 元中由于大变形而出现的网格畸形问题[8],同时,其 计算精度及计算效率都比较高,因此,近年来在国内 外受到了诸多研究者的推崇[9-12].
目前,耦合的物质点方法主要可分为两种形 式[13]:一种是基于v-p格式,也就是以固体颗粒的速度和孔压作为未知量,这种格式的结构相对简单,但是不能考虑流体-固体间的相对速度;另一种则是基于v-w 格式,也就是以固体的速度以及流体的速度作为未知量,这种格式考虑更为全面,但是由于流体速度和固体速度同阶积分,使得程序的稳定性比较 欠缺.Zhang等[14]最先将物质点方法应用到孔隙介质分析中,但是由于针对流体、固体采用了同阶的积分形式,在考虑整体程序稳定性的前提下,这种方法 仅能分析小变形问题,却牺牲了物质点在大变形分析中的优势和特点.Jassim等人[15]则基于混合物理论提出了v-w 形式下的流固耦合方法,目前它也是 物质点流固耦合方法中使用最为普遍的,它通过依次求解基于固体以及混合物的动量守恒方程,先后 获得固体颗粒及流体颗粒的速度,并且通过高斯积分来提高应力计算精度,但是由于物质点在背景网 格中的流动性,很难保证网格的质量和网格中的物质点的质量相等,因此质量难以保证守恒.Bandara和Soga[16]则基于混合物理论,推导了基于两套颗粒(一套表征固体,另一套则表征流体)的物质点流固耦合控制方程,并且通过引入B-bar型函数在物质点 上直接求解孔压以防止出现应力自锁的现象,但是 由于两套颗粒的使用,程序的稳定性以及计算效率都大幅降低.Yerro等[17]则在随后的研究中又重新 使用了一套颗粒,通过流体、固体之间的比例来确 定每个颗粒的组分组成,并且进一步推导了在非饱和情況下液相-气相-固相的全耦合控制方程,但由于气相的引入,使得这种方法在较大(极端)变形的情况下会引起程序的不稳定,从而降低了方法的适用性.
本文基于连续介质力学的质量以及动量守恒原理,同样使用了一套颗粒,在考虑极端变形的情况下,通过引入饱和度简化考虑了非饱和土的力学行为,推导并提出了流固耦合物质点方法(CMPM),可求解流固耦合下岩土结构的极端变形问题.在构建 这样一个流固耦合控制方程的时候,虽然使用饱和度简化考虑了气相,但在实用性上增加了程序的稳 定性.另一方面,降雨滑坡问题则是一个典型的非饱和问题.因此,本文首先比较了经典的一维非饱和土 渗流试验(Liakopoulos test),以及Terzaghi一维固结试验(饱和度设置成1的时候,程序即可从非饱和的情况退化为饱和的情况),以证明 CMPM在饱和/非 饱和土力学行为模拟中的适用性,最后,进一步结合 降雨滑坡算例,验证了方法在解决降雨诱发滑坡模拟问题中的可行性.
1耦合物质点法
基于连续介质力学的质量以及动量守恒原理,本节针对基于速度场(v-w formulation)的物质点流
固耦合系统控制方程进行了详细的推导.
1.1控制方程
基于连续介质力学的质量以及动量守恒原理,任意连续体的系统控制方程可以表示为
1.2 控制方程的弱形式
至此,基于速度场的流固耦合控制方程已经全 部得出,即流体的动量守恒方程(公式(12)),以及混 合物的动量守恒方程(公式(15)).在相应的公式中,两边同时乘以加权函数wh,并在相应积分区域进行积分即可得到动量平衡方程的弱形式.
采用分部积分,将应力项展开,并结合散度定理,水的动量平衡方程为
1.3控制方程的离散化
不同于有限元方法,应力应变选择在高斯点上 进行积分,物质点法中通常直接在物质点上进行积分.为描述清晰,物质点方法离散示意图如图1所示,其中上标“0”表示连续体初始状态,“1”表示变形 后状态.物质点用于表征结构本身,储存和结构本身相关的一切信息以及状态变量;背景(欧拉)网格仅用于求解控制方程,网格节点信息不进行存储.通过背景网格上的形函数,物质点上的信息与节点上的信息可以直观地联系起来,构造于积分区域上的控 制方程也就可以转化为物质点上信息的求和.
以物质点质量mp 求解为例,物质点方法将原始构形中的连续体分解成Np个材料点集合,同时认为,每个物质点在空间上占据有相应的体积区域,但不一定需要明确具体的形状,在对应区域内,存在质量,而在区域外,质量即为零.因此,任一物质点的质量即可表达为连续体的空间密度在其相应区域上的积分,即
值得注意的是,饱和状态下的流固耦合控制方程,其原理与非饱和情况下的推导计算过程大体相同,只需将饱和度设置为1,控制方程即可直观地退化成饱和状态下的动量守恒方程.这里不做详细介绍,可留给读者做简要推导.
1.4 耦合物质点方法(CMPM)的计算步骤
为了求解控制方程,不仅在空间上需要对公式(23)(24)进行离散,同时也需要对其在时间维度上 进行离散.因为将质量矩阵离散为对角形式,其在存 储时就可存储为向量的形式.于是,在整个控制方程 求解时,避免了大型的矩阵运算,可以通过向量运算直接求解,而在时间上的迭代则选择了中心点插值的显示积分形式.
相比较于有限元分析中更广泛使用的v-p 格 式,耦合物质点方法采用了基于速度场的v-w 格式,其有两个优点:1)积分过程中,时间步长的选择更为宽松[17],可以提高计算效率,节省计算时间;2)避免了大型矩阵运算,求解过程更为直接.综合起来,耦 合物质点方法算法步骤总结如下.
1)将储存在物质点上的信息映射到背景网格 上,初始化节点上所有变量.
2)求解流体(水)相的加速度,见公式(23).
3)求解固相的加速度,见公式(24).
4)更新节点上流、固两项的速度.
5)更新物质点上流、固两相的速度,然后根据计算得出的速度更新物质点的位置.
6)基于物质点上新的速度,返回映射更新节点 上的速度,基于速度梯度,计算物质点上的应力和水压力.
7)重置背景网格,开始下一个计算周期.
2 数值算例
2.1一维固结试验
图2(a)给出了一维固结试验示意图,砂柱高1m、宽0.1m,处于完全饱和状态.在砂柱上表面处(由于变形小而在边界节点处)施加10kPa的压力.假定 两侧和底部不排水,仅允许水从顶面排出.数值计算中,将砂柱离散成10个等大小的四边形单元,尺寸为0.1m×0.1m.使用各向同性的线弹性材料对砂土 颗粒力学行为进行模拟,材料参数选择见表1,时间 步长为1.0×10-7 s,共計算1.0×107 步.
图2(b)给出了耦合物质点法(CMPM)的计算结果,并与Terzaghi理论解进行了对比.对于各种时间 因子 Tv 绘制图的等时线,如图2所示,其中
由于应用了低阶线性单元,孔隙水压力在每一个单元内是恒定的,而每个单元使用了上下两排共 4个积分点,因此孔隙水压力呈阶梯状分布特征,但总 体而言,孔隙水压力均匀分布在太沙基理论解的两 边,因此,物质点方法在解决饱和土体的流固耦合问题上是适用的.
2.2 非饱和土的入渗试验
为了验证考虑非饱和状态下的耦合物质点法(CMPM)的适宜性,本节采用并分析了Liakopoulos[19]一维非饱和砂土的入渗试验.试验装置如图3所示,高1m,宽0.1m,试样采用了Del Monte 砂,材料特性参数参见表2.
试验具体分为两个部分,试验准备阶段和试验 本身.试验准备阶段,在柱样容器内均匀布满砂子,然后从砂柱顶部不断注水,直至整个试样处于完整 饱和的状态;试验开始后,停止注水,两个侧壁不可透水,而水能够从底部自由排出,这样,砂柱上半部分逐渐呈现非饱和状态,沿砂柱高度均匀布置吸力计,用于测量砂柱内部吸力分布.为计算简便,假定气体压力等于大气压力.
对于土水特征曲线的选择,Lewis等[20]认为当饱和度Sw >0.91时,其可采取以下格式:
数值计算中,同样将砂柱离散成10个大小一样、尺寸为0.1m×0.1m的四节点四边形单元,时间 步长为5.0×10-6 s,共计时长120min.试验过程中,记录了砂样在不同时刻的饱和度、垂直位移、毛细压力随高度的变化,并与Liakopoulos 试验进行了对比,结果如图4所示.
整体而言,计算结果与试验结果吻合较好,说明了该方法在非饱和土中的适用性.同时,如图4所示,随着水从砂柱样中逐渐渗出,砂柱顶部逐渐形成非饱和状态,形成毛细水吸力,饱和度变化逐渐减 慢,相应地,水流出速度也逐渐降低.
2.3 降雨滑坡算例
最后,为探究耦合物质点法(CMPM)在滑坡模拟中的适宜性,本节探讨了边坡在两种不同降雨条件下的失稳破坏过程.
边坡的几何尺寸如图5所示,高度为10m,坡度为45°,土体特性参数如表3所示.数值模型的背景网格尺寸为0.5m×0.5m,每个单元网格基于高斯点位置插入4个物质点,边坡结构本身表征使用了3720个物质点.初始孔压设置为-50kPa.降雨边界条件通过孔压边界条件施加,即所有的降雨量都渗入边坡内部,不形成表面径流.边坡内部土体假设为理想弹塑性材料,破坏准则服从摩尔-库伦强度准则.
2.3.1第一类降雨(持续降雨)直至产生深层破坏
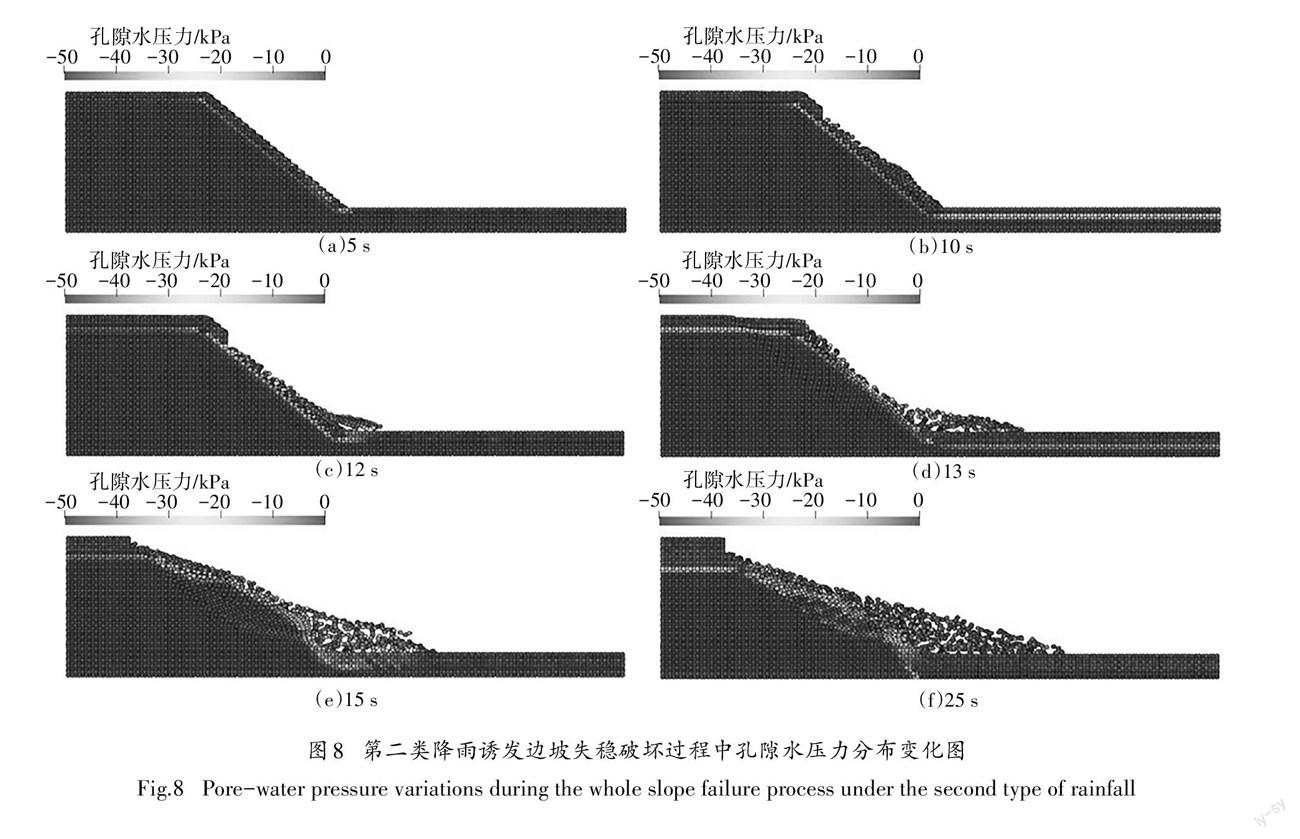
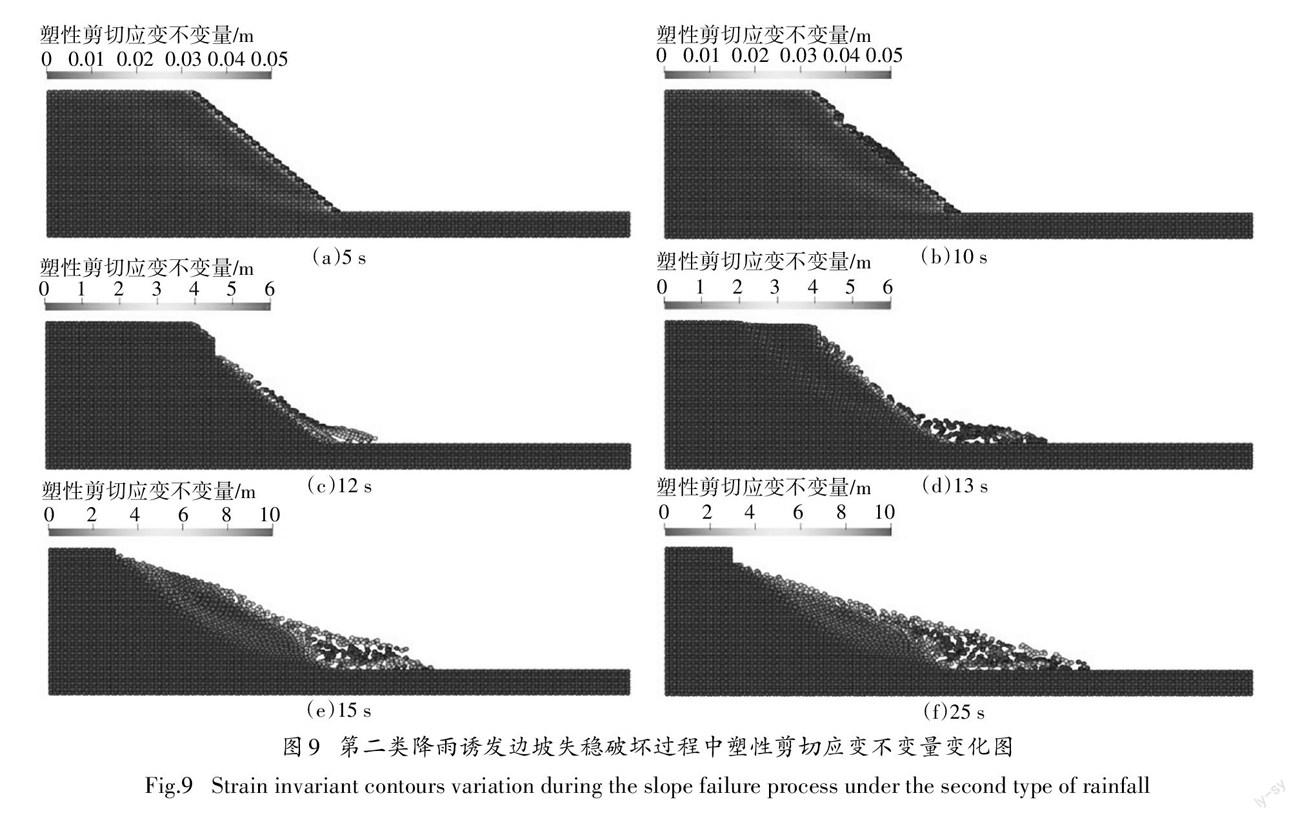
图6(a)~(f)和图7(a)~(f)分别展示了不同时刻下以孔隙水压力和塑性剪切应变不变量为指标的边坡破坏过程.由图6可看到,降雨入渗将导致边坡表面形成湿润区,孔隙水压力为0,湿润区以下的土体未受到影响,孔隙水压力为初始值-50kPa.随着入渗时间的增加,湿润区深度逐渐增加,5 s和10s的入渗深度分别为0.83m 和 1.36 m,最终在边坡表层土体重度的作用下,约在 12 s时边坡发生了较大位移,约在15 s时发生显著变形的失稳破坏,此时入渗深度为1.86 m.随着进一步入渗的发生,边坡肩部后缘的土体也发生了坍塌破坏,如图6(f)所示. 由图7可看到,降雨入渗过程中边坡产生了两条滑移面,一条位于边坡表层,一条位于边坡内部约3m的位置.边坡发生破坏时,土体沿着深层滑面形成了整体滑动趋势,而后表层滑移面发生加速滑动,塑性应变不变量显著增加,如图7(c)(d)所示;直至25 s时,滑体在新位置上达到新的平衡,共产生滑动距离约为12.8 m,如图7(e)~(f)所示.2.3.2第二类降雨(短暂降雨)产生浅层剥蚀破坏降雨时间设置为8 s,之后任其自由下渗 . 图8 (a)~(f)和图 9(a)~(f)分别展示了不同时刻下以孔隙水压力和塑性剪切应变不变量为指标的边坡破坏 过程.由图8和图9可以看到,在短暂降雨的入渗条 件下,边坡在降雨结束时首先发生了表层剥蚀破坏,剥蚀土体的滑动距离约为5.8 m;随着入渗时间的增加,湿润区逐渐增大,约在12 s时边坡肩部发生了较大位移,约在15s时土体沿着深层滑移面发生滑动,边坡发生显著变形的失稳破坏.25 s时滑坡体的滑动距离约为8.6 m.
综上所述,本算例中降雨诱发边坡失稳破坏主 要是由于边坡表层基质吸力的降低(负孔隙水压的消散)而引起的.两类不同的降雨条件很鲜明地揭示了两种不同的破坏模式,持续降雨条件下,边坡易形成深层滑面,引起整体的滑动,浅层破坏则更多是由于深层破坏引起的二次破坏,这种破坏模式下的滑动距离主要由初始的深层破坏控制;短暂降雨条件下破坏模式则主要表现为表层的剥蚀破坏,而当初 始的剥落量变得足够大时,就会进而引起渐进式的深层破坏,这种破坏模式主要依赖于边坡浅层的破 坏程度.总而言之,CMPM 能够较好地模拟降雨诱发的边坡失稳破坏过程.
3结论与展望
基于连续介质力学的质量以及动量守恒原理,考虑固-液两相非饱和材料的水力耦合作用,本文推 导了基于速度场(v-w formulation)的考虑固-液两相耦合的系统控制方程.结合 Terzaghi一维固结试验、Liakopoulos 非饱和土的入渗试验,以及边坡在不同 降雨条件下的破坏过程再现,验证了该计算模型在模拟非饱和土的水力耦合相互作用问题上的可靠 性,对准确评价降雨滑坡的破坏过程具有重要的理论与实际指导意义.
目前的物质点流固耦合模型(CMPM)虽然通过简化引入饱和度近似模拟了降雨入渗边坡的过程,可大幅度提高程序的稳定性,但是对于耦合物质点方法的发展及应用依然有很多工作需要开展:
1)针对流固耦合问题,程序的稳定性依然是物质点方法发展的一个瓶颈,引入B-bar 形函数,使用分步法(fractional step algorithm),抑或对物质点上孔 压进行光滑化等数值手段,需要进一步探究;
2)目前的工作仅讨论了孔压边界下降雨诱发边 坡破坏的过程,加入流量边界,探讨不同降雨强度以及降 雨模式下边 坡 破 坏 过程 也是下一步 需 要研究的.
参考文献
[1]黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):433-454.
HUANG R Q.Large-scale landslides and their sliding mecha-nisms in China since the 20th century [J].Chinese Journal of Rock Mechanics and Engineering,2007,26(3):433-454.(In Chinese)
[2]王思敬.工程地质学的任务与未来[J].工程地质学报,1999,7(3):195-199.
WANG S J.Tasks and future of engineering geology[J].Journal of Engineering Geology,1999,7(3):195-199.(In Chinese)
[3]蒋承菘.中国地质灾害的现状与防治工作[J].中国地质,2000,27(4):3-5.
JANG C S.Present situation and prevention of geological disasters in China [J].Chinese Geology,2000,27(4):3-5.(In Chinese)
[4]殷跃平.中国地质灾害减灾回顾与展望:从国际减灾十年到国际减灾战略[J].国土资源科技管理,2001,18(3):26-29.
YIN Y P.A review and vision of geological hazards in China[J].Management Geological Science and Technology,2001,18(3): 26-29.(In Chinese)
- 杨峰,林斐然,鲁千国.深圳一工业园山体滑坡 59人失联[EB/OL].(2015-12-21)[2021-06-29].http://epaper.bjnews.com.cn/ html/2015-12/21/content_614615.htm?div=-1.YANG F,LIN F R,LU Q G.Fifty-nine people are missing after a landslide at an industrial park in Shenzhen[EB/OL].(2015-12-21)[2021-06-29].
http://epaper.bjnews.com.cn/html/2015-12/ 21/content_614615.htm?div=-1.(In Chinese)
[6]李芬,鄭威,郭锐.土石混杂高边坡稳定性分析数值方法研究[J].湖南大学学报(自然科学版),2018,45(S1):74-79.
LI F,ZHENG W,GUO R.Study on numerical method of stability analysis for earth-rock mixed high slope [J].Journal of Hunan University(Natural Sciences),2018,45(S1):74-79.(In Chi-nese)
[7]彭文哲,赵明华,肖尧,等.抗滑桩加固边坡的稳定性分析及最优桩位的确定[J].湖南大学学报(自然科学版),2020,47(5): 23-30.
PENG W Z,ZHAO M H,XIAO Y,et al.Stability analysis of anti-slide pile reinforced slope and determination of optimal pile posi-tion[J].Journal of Hunan University(Natural Sciences),2020,47(5):23-30.(In Chinese)
[8]SULSKY D,CHEN Z,SCHREYER H L.A particle method forhistory-dependent materials [J].Computer Methods in AppliedMechanics and Engineering,1994,118(1/2):179-196.
[9]WI?CKOWSKI Z,YOUN S K,YEON J H.A particle-in-cell solu-tion to the silo discharging problem[J].International Journal for Numerical Methods in Engineering,1999,45(9):1203-1225.
[10]HU W Q,CHEN Z.Model-based simulation of the synergistic ef-fects of blast and fragmentation on a concrete wall using the MPM[J].International Journal of Impact Engineering,2006,32(12): 2066-2096.
[11]NAIRN J A.Material point method calculations with explicit
cracks[J].CMES:Computer Modeling in Engineering & Sciences,2003,4(6):649-664.
[12]WI?CKOWSKI Z.The material point method in large strain engi-neering problems [J].Computer Methods in Applied Mechanics and Engineering,2004,193(39/40/41):4417-4438.
[13]VAN ESCH J,STOLLE D,JASSIM I.Finite element method for
coupled dynamic flow-deformation simulation [C]//2nd Interna-tional Symposium on Computational Geomechanics.2011.
[14]ZHANG H W,WANG K P,ZHANG Z.Material point method for
numerical simulation of failure phenomena in multiphase porous media [M]//Computational Mechanics. Berlin, Heidelberg: Springer,2009:36-47.
[15]JASSIM I,STOLLE D,VERMEER P.Two-phase dynamic analy-sis by material point method[J].International Journal for Numeri-cal and Analytical Methods in Geomechanics,2013,37(15): 2502-2522.
[16]BANDARA S,SOGA K.Coupling of soil deformation and pore
fluid flow using material point method[J].Computers and Geotech-nics,2015,63:199-214.
[17]YERRO A,ALONSO E E,PINYOL N M.The material point
method for unsaturated soils [J].Géotechnique,2015,65(3): 201-217.
[18]VAN GENUCHTEN M T.A closed-form equation for predicting
the hydraulic conductivity of unsaturated soils[J].Soil Science So-ciety of America Journal,1980,44(5):892-898.
[19]LIAKOPOULOS A C.Transient flow through unsaturated porous
media[D].Berkeley:University of California,Berkeley,1964.
[20]LEWIS R W,SCHREFLER B A.The finite element method in the
static and dynamic deformation and consolidation in porous media[M].Hoboken,NJ,USA:John Wiley and Sons,1998.

