小题压轴 构建支架 凸显本质
陈冬


【摘 要】 选择题、填空题的压轴题虽为一道小题,但其题量内涵、知识外延、思维的广度与深度、选拔的区分度与难度等都会有所提升,如果按常规的解题技巧和方法去做,可能花了较多时间算出来还是模棱两可的结果.为此,压轴小题常有其独特的解题思路和策略,构建恰当、合理的情境支架,多方位、多角度构建情境支架,既有利于压轴小题思路的展开与延伸,又激发了压轴小题本质的凸显与深化.
【关键词】 情境;支架;本质
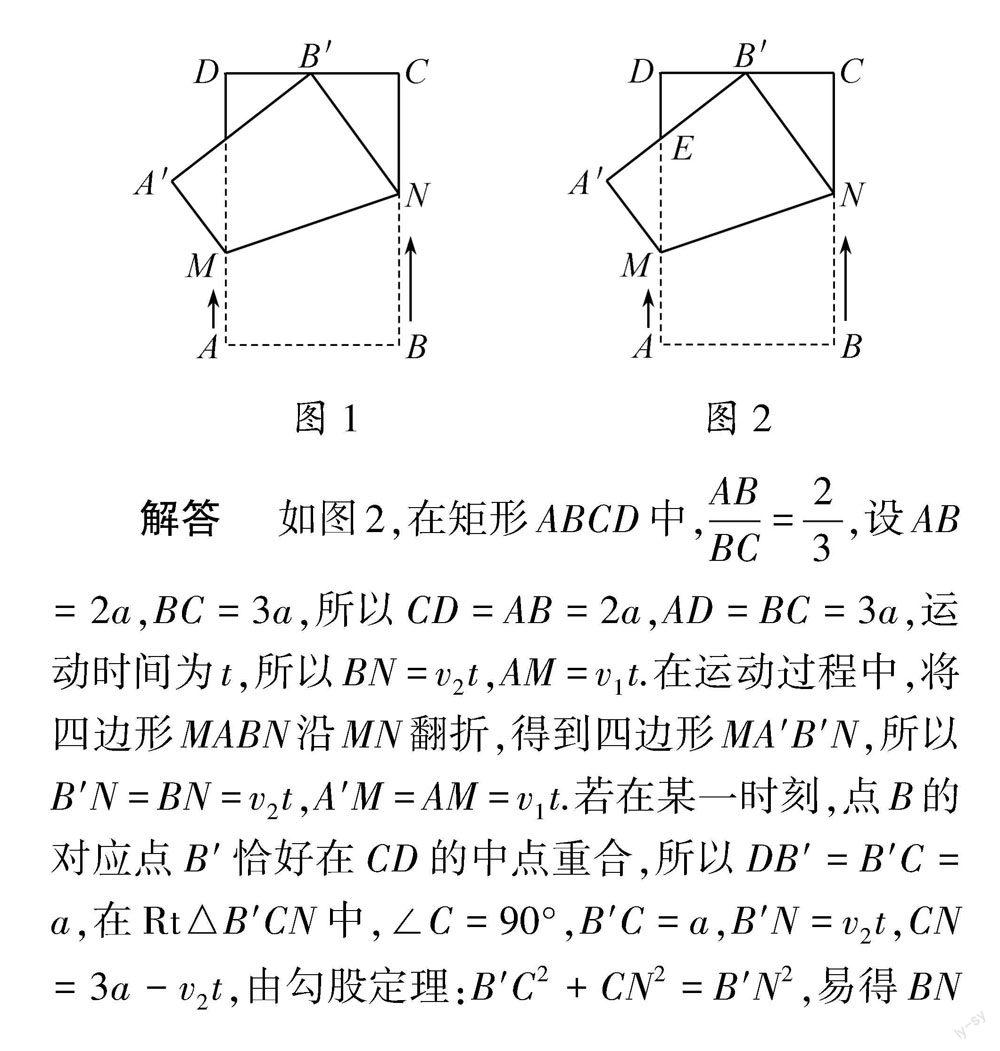
原题呈现 (2022年江苏省苏州市中考第16题) 如图1,在矩形 ABCD中, AB BC = 2 3 .动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为v 1,点N运动的速度为v 2,且v 1 分析 本题属于矩形背景下的动点问题、翻折问题,涉及到矩形的性质、翻折性质、轴对称性质、中点性质、两个三角形相似的判定与性质、勾股定理及两个三角形全等的判定与性质等知识点,熟练掌握相關判定及性质,求出相应线段长是解决这道压轴题的关键. 解答 如图2,在矩形ABCD中, AB BC = 2 3 ,设AB=2a,BC=3a,所以CD=AB=2a,AD=BC=3a,运动时间为t,所以BN=v 2t,AM=v 1t.在运动过程中,将四边形MABN沿MN翻折,得到四边形MA′B′N,所以B′N=BN=v 2t,A′M=AM=v 1t.若在某一时刻,点B的对应点B′恰好在CD的中点重合,所以DB′=B′C=a,在 Rt △B′CN中,∠C=90 ° ,B′C=a,B′N=v 2t,CN=3a-v 2t,由勾股定理:B′C2+CN2=B′N2,易得BN=v 2t= 5 3 a. 因为∠A′B′N=∠B=90 ° ,所以∠A′B′D+∠CB′N=90 ° .因为∠CNB′+∠CB′N=90 ° ,所以∠A′B′D=∠CNB′,所以△EDB′∽△B′CN,所以 DE DB′ = B′C CN = B′C BC-BN = a 3a- 5 3 a = 3 4 . 因为DB′=B′C=a,所以DE= 3 4 DB′= 3 4 a,则B′E= (DB′)2+DE2 = a2+ 3 4 a 2 = 5 4 a,所以A′E=A′B′-B′E=2a- 5 4 a= 3 4 a,即DE= 3 4 a=A′E. 在△A′EM和△DEB′中, ∠A′=∠D=90 ° ,A′E=DE,∠A′EM=∠DEB′, 所以△A′EM≌△DEB′( ASA ),所以A′M=B′D=a,即AM=v 1t=a,所以 v 1 v 2 = v 1t v 2t = AM BN = a 5 3 a = 3 5 . 解后思考 上述解答实为本题的通式通法,充分利用图形翻折、矩形的性质、中点性质、相似三角形的判定与性质、勾股定理及全等三角形的判定与性质等诸多知识,最终解决了两动点的速度之比问题.但回头细想,本题为填空式压轴题,涉及的知识点多、计算量大,学生在较短时间内解决这个问题,必定要费些周折.那有没有快捷、有效的解题思路方法呢?答案是肯定的,我们来欣赏几种解法. 1.特殊值法 分析 此题用这个特殊值作情境支架的话,可以简化参数带来的繁琐,可能比较贴近学生的思维,学生更容易上手解答.当然作为填空题,这样做也不会影响最后正确答案的得出. 简答 如图3,由题中 AB BC = 2 3 ,我们不妨设AB=2,BC=3,则AB=CD=2,AD=BC=3,由点B′为CD的中点,可得DB′=B′C=1.在 Rt △B′CN中,由勾股定理:B′C2+CN2=B′N2,易得BN=B′N= 5 3 ,CN= 4 3 .由∠A′B′N=∠C=∠D=90 ° ,易证△EDB′∽△B′CN,于是便可得DE= 3 4 ,B′E= 5 4 ,又A′B′=AB=2,易得A′E= 3 4 ,然后发现△A′EM≌△DEB′( ASA ),可得A′M=B′D=1,即AM=A′M=1,则 v 1 v 2 = AM BN = 1 5 3 = 3 5 . 2.K模型法 分析 本题通过翻折发现图中存在“K”字形这个基本图形,然后直接利用“K”字模型作情境支架,将三角形问题“模块”化,利于拓展解题思路,提高解题效率.当无法直接发现“K”字形图,欲利用这种基本模型来解决问题,可以通过添加辅助线的方法,构造出我们熟悉的K模型.当然,“K”字形图一般为“一线三垂直”形式,从中可以得出两三角形全等或相似.有时我们可将垂直条件弱化,同样可以构造出“K” 字形图. 简答 如图4,我们可以在原题解答的基础上,连接MB和MB′,利用翻折可知MB=MB′,易证△MDB′≌△BAM,于是AM=DB′=a,则 v 1 v 2 = v 1t v 2t = AM BN = a 5 3 a = 3 5 . 3.十字架模型法 分析 “十字架模型”是数学平面几何中比较重要的一个模型.常见的类型有正方形中的十字架和矩形中的十字架.本题除了由折叠的性质得到图形全等外,还能由轴对称分析得出:对称轴垂直平分对应点之间的连线段.为此,我们构建这个“十字架模型”作情境支架,引导学生透过表象,抓住本质看问题,充分挖掘解题模型隐含着的关键信息和特征条件,学生就能进一步实现知识的迁移应用,拓宽思维,加深对模型的全面理解,提高解题能力[1]. 简答 如图5,连接BB′,过点M作MG⊥BC于G.BB′与MN构成“十字架”,由翻折可知BB′⊥MN,易证△MNG∽△BB′C,得 MG BC = NG B′C ,由MG=AB=2a,B′C=a,BC=3a,得出NG= 2 3 a,再由NB= 5 3 a,可得出AM=BG=a,则 v 1 v 2 = v 1t v 2t = AM BN = a 5 3 a = 3 5 . 4.角平分线+平行线等腰三角形 分析 角平分线与等腰三角形有着紧密的联系.比如,在许多几何问题中,遇到等腰三角形就会想到顶角的平分线,遇到角平分线又会想到构造等腰三角形.当一个图形里出现角平分线和平行线时,我们发现图中会出现两角相等或两线段相等,即“角平分线+平行线等腰三角形”.本题我们可构建这个模型作情境支架,透过表面现象,挖掘本质属性,便会从中归纳出某些规律性的东西,并可以用这个共性结论去指导解决类似的问题[2]. 简答 如图6,其实这道题的难点在于如何求AM的长度,我们可以延长NB′和AD,两延长线交于点H.由翻折知∠MNB=∠MNB′,由AD∥BC可得∠MNB=∠DMN,则∠MNB′=∠DMN,于是有HM=HN.易证△HDB′≌△NCB′,则有HB′=NB′= 5 3 a,HD=NC= 4 3 a,于是有HM=HN= 10 3 a,DM=HM-HD= 10 3 a- 4 3 a=2a,所以AM=AD-DM=a,则 v 1 v 2 = v 1t v 2t = AM BN = a 5 3 a = 3 5 . 5. 建立坐标系法 分析 一般来说,几何问题较多利用几何图形的性质与判定来解,但如果我们跳出这个框框,构建适当的平面直角坐标系作情境支架,从中可以说明或确定某些点的位置、运动的快慢、方向等.因此,我们可以在此坐标系中,按规定方法选取有次序的一组数据,即“坐标”,利用这些点的坐标就能计算线段的长度或求解出直线的函数解析 式.笔者以为这种想法会让同学们对坐标法的作用有更进一步认识,这是坐标系里由两点坐标得到线段长或直线解析式的具体途径,其实也是一个由“数”到“形”的过程,是我们破解压轴题应该具备的技能. 简答 此题虽为几何问题,但建立坐标系来解也不失为一种好方法.我们可以以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图7的直角坐标系,连接BB′交MN于K.由题中 AB BC = 2 3 ,可设AB=2a,BC=3a,则B(2a,0),C(2a,3a),D(0,3a),B′(a,3a),由翻折知BB′⊥MN且K为BB′的中点,于是点K( 3 2 a, 3 2 a),可求得k BB′=-3,由BB′⊥MN知k MN= 1 3 ,可得直线MN的解析式为y MN= 1 3 (x- 3 2 a)+ 3 2 a,易求M(0,a),N(2a, 5 3 a),则AM=a,BN= 5 3 a,所以 v 1 v 2 = v 1t v 2t = AM BN = a 5 3 a = 3 5 . 综上所述, 小题虽小,但作为压轴题, 得满分似乎比大题更难,因为鉴于试题容量、试题表述等诸多因素, 压轴小题的描述相对更为精炼, 而压轴大题的描述则比较详细. 正因为这样, 压轴小题显得更难, 解答时花费时间多, 而且一不留意就要做错或一时找不到有效的方法.为此, 很多同学看到压轴小题一般就是一猜二蒙三放弃.但笔者认为,同学们要敢于嘗试压轴小题,所有难题背后涵盖的就是解题技巧和方法.只要同学们能熟练掌握数学模型和通性通法, 构建合适的情境支架,深挖问题内在的本质,善于灵活机动,精于相互验证,压轴小题自然会迎刃而解. 参考文献 [1] 施长燕.巧用K字型,品基本图形在相似中的妙用[J].中学课程辅导(教师通讯),2016(18). [2] 梁珏,朱宸材.难舍难分的角平分线与等腰三角形[J].中学生数理化(八年级数学),2015(09).
中学数学杂志(初中版)2022年5期
