理解中位线定理的生成

林龙海

摘要：现行义务教育数学课程标准中指出，数学教学中，要把每节课教学的知识置于整体知识的体系中，要注重知识的“生长点”与“延伸点”，要处理好整体与部分之间的关系，某些数学知识可以从不同的角度加以分析、从不同的层次加以理解.鉴于此，笔者围绕三角形的中位线定理，以及三角形中位线定理在不同知识系统中的安排，解读人教版教材编排意图，在理解数学知识点所处的知识网络背景，理解学生已有的认知经验、认知结构的基础之上，优化教学过程，生成有效课堂.

关键词：三角形中位线;教材编排;教学处理

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）20-0005-03

1 三角形中位线定理的源起

三角形中位线的相关知识起源于古代两河流域古巴比伦时期（公元前1800-公元前1600）现实生活中土地大小的财产分割.三角形中位线等于底边的一半，这一性质早为三千多年前的古人熟知.再到公元前3世纪，古希腊数学家欧几里德在《几何原本》卷六里给出了更一般的命题：“将三角形两腰分割成成比例的线段，则分点连线段平行三角形的底边”.

了解数学史帮助我们了解人类的认知经验的形成过程，可见基于生产生活的需要，数学早期要解决的问题都是与面积大小财产分割有关的经济问题.而变换是现代几何的核心思想. 2001年发布的《全日制义务教育数学课程标准（实验版）》，第一次把图形变换纳入义务教育数学课程内容，《义务教育数学课程标准（2011年版）》则在“图形的变化”这个板块里，整合了图形变换的课程内容.从2001年开始，各版本的初中数学教科书都把图形变换作为几何的重要内容组织进课程资源，这说明从2001年开始，在几何内容中渗透变换思想成为我国几何课程教学的重要价值取向.

2 三角形中位线定理在不同版本教材中的编排

在国内现行的义务教育九个版本的数学教材中，北京师范大学出版社在第六章《平行四边形》中安排三角形的中位线;湖南教育出版社八年级下册第2章《四边形》在平行四边形、中心对称和中心对称图形之后安排三角形的中位线;河北教育出版社八年级下册第二十二章《四边形》在平行四边形的性质和判定之后安排三角形的中位线;浙江教育出版社八年级下册第4章《平行四边形》在中心对称和平行四边形的判定定理之后安排三角形的中位线;江苏科学技术出版社八年级下册第9章《中心对称图形-平行四边形》在图形的旋转，中心对称，平行四边形，特殊的平行四边形之后安排三角形的中位线;青岛出版社八年级下册第6章《平行四边形》在平行四边形性质和判定以及特殊的平行四边形之后安排三角形的中位线定理.

这六种教材在相应的数学知识的系统编排中主要是在平行四边形的知识网络中安排三角形中位线定理，其中发现中位线性质主要是测量，观察，操作的途径，证明方法主要是平行四边形法.另外，上海科学技术出版社八年级下册第19章《四边形》在平行四边形内容中，用平行四边形的判定和性质先证明平行线等分线段，再得出经过三角形一边中点与另一边平行的直线必平分第三边的推论，最后利用同一性证明得到三角形中位线定理.而华东师范大学出版社（华师大版）则是在九年级上册第23章《图形的相似》的成比例线段，相似圖形，相似三角形之后安排中位线，用相似三角形的判定和性质来证明三角形中位线定理.证明的方法有欧式面积法，同一法，平行四边形法，反证法等.

2.1 欧式面积法

如图1，在△ABC中，点D、E分别是AB、AC的中点，连接BE、CD，则S△BCD=S△BCE=12S△ABC，所以DE∥BC;另一方面，S△BDE=12S△ABE=12S△EBC，而△BDE和△EBC是等高的，所以DE=12BC.

2.2 同一法

如图2，在△ABC中，点D、E分别是AB、AC的中点，过D作BC的平行线，交AC于E′，则AE′=E′C，因此DE、DE′重合，故DE∥BC，可得△ADE∽△ABC，所以DEBC=ADAB=12，从而得到DE=12BC.

2.3 平行四边形法

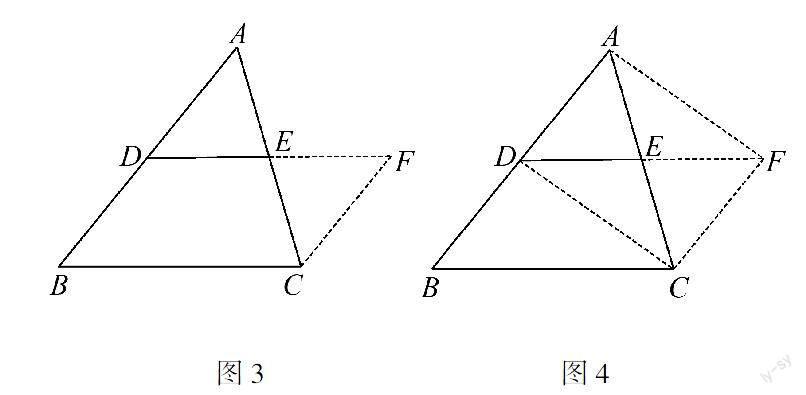
如图3，延长DE到F，使FE=DE，连接CF.易证△ADE≌△CFE，所以∠A=∠ECF，AD=CF.可得CF∥AB，CF=BD.所以四边形DBCF是平行四边形，从而得到DE∥BC，DE=12BC.

以上大都是在一般化的平行线分线段成比例公理认识上，发现并提炼出特殊化的推论，三角形中位线性质，而平行四边形法主要是依据平行四边形的判定和性质来证明三角形中位线定理，其中不同版本的证明差异也只是细枝末节上的差异.比如人民教育出版社（下文简称人教版）的证明用图4，内核是平行四边形法，证法稍简洁，但证明对学生图形分解能力要求更强.

3 理解人教版教材三角形中位线定理的编排意图义务教育阶段，教材的编排体系直接影响学生的认知结构，了解学生已有的认识，是理解学生认知的生长点.在小学阶段，学生对几何图形面积的认识链是从单位正方形开始，然后扩充到一般的正方形，再伸展到长方形，割补到平行四边形，再分切成三角形，因此小学生是先认识了平行四边形的面积S=ah，再获得三角形的面积公式S△=12ah.人教版初中几何教材的内容编排结构是怎样的？七年级上册第四章《几何图形初步》安排几何基本概念，直线、射线、线段、角.在七年级下册第五章《相交线与平行线》中编排了命题与定理，平移.八年级上册《三角形》《全等三角形》之后，第十三章《轴对称》安排了轴对称与轴对称图形，等腰三角形，等边三角形，最后安排了含30°角的直角三角形，该图形性质是利用等边三角形的轴对称性一分为二成两个含30°角的直角三角形，发现特性并可以利用这样的整体与部分的转化构造图形并证明该性质.八年级下册《勾股定理》之后安排第十八章《平行四边形》18.1研究平行四边形性质和判定之后编排三角形中位线定理的内容.九年级上册第二十三章图形变换《旋转》，第二十四章《圆》，九年级下册第二十七章《相似》27.3安排图形位似变换.

可见人教版几何内容的编排是图形变换与图形相伴而行，呈双螺旋式上升的结构.在平行四边形章节安排三角形中位线定理，是从图形变换的角度进行编排，教学研究离不开研究教材，应是见树木更见森林，见森林才见树木下整体构建知识体系.图形变换体现从整体到部分，部分到整体的辩证统一思想.理解数学，理解学生，更好的理解教材编排意图，那么对比学生在八年级上册认识并证明含30°角的直角三角形性质的过程，是在轴对称变换下的生成过程中发生的，以及小学阶段的学生已有的几何图形认识结构，学生的已有经验也支持他们继续从图形变换的土壤中生长发现、理解并证明三角形中位线定理.

4 基于理解人教版教材的教学处理

基于理解人教版教材的编排意图，从有利于学生形成研究一个几何图形的完整经验考虑出发，三角形中位线定理的教学设想是紧扣图形变换之中心对称，抓住平行四边形与三角形之间整体与部分的关系，由学生直观观察发现特殊事物，学生再尝试描述特殊事物时抽象精炼图形构件，对新构件下定义，用新定义描述图形特性.在逻辑推理证明三角形中位线性质时，由部分还原整体，通过平行四边形法证明，获得定理.

如图5，有硬纸板做的一个平行四边形，把一根细木条固定在平行四边形的对角线的交点O处，使细木条可以绕着点O转动.拨动细木条，发现了什么，并证明你的发现.（该习题源自人民教育出版社义务教育教科书数学八年级下册教材51页，是教材原题，可借由GeoGebra软件或几何画板软件呈现）

由学生通过直观观察发现特殊（图6），精炼事物抽离本质，描述属性，这里用数学的语言描述事物是难点（图7），但恰是能力打磨点，必要的经验积累點.

学生尝试定义三角形的中位线（图7），用数学语言描述三角形中位线性质，教师帮助. 然后在公理、定理体系下逻辑推理证明三角形中位线性质时，还原整体，构造平行四边形（图8），用平行四边形法证明获得定理. 之后的教学，或是讨论证明细节（如图9，图10），或是引入欧式面积法，都可以因时因地因人制宜灵活处理.

5 教学研究启示

教育教学工作者在一线经常遇到数学教学中的各种问题，纠其原因是复杂的，既有学生认知水平的差异，家庭教育环境的差异，也有教师课堂组织教学的过程中没有找准学生知识的生长点，学生获得新知的体验过程不够深刻等原因.“四个理解”需要教师切实地进行教学研究工作，而教育教学研究的施力点在于系统地理解教材，研读教材的整体架构，知识间的逻辑关系、重要细节等等，这样才能接近数学的原貌理解数学，这样才能走近学生，才能把数学教学工作做到实处.

参考文献：

[1] 李霞，汪晓勤.三角形中位线定理的历史[J].数学教学月刊，2016（9）：58-60.

[2] （古希腊）欧几里得.兰纪正，朱恩宽译.几何原本[M].西安：陕西科学技术出版社，2003：153-154.

[3] 吴增生.三角形中位线定理教材设计之我见[J].中国数学教育，2018（12）：3-5.

[责任编辑：李璟]