在活动中思考 在思考中体验

杨牛扣

数学概念是数学教学的核心，是学生思考问题、解决问题的源泉。学生数学能力的提升，本质上取决于对数学概念理解的深刻程度。“全等”是初中数学最为基础的概念，也是核心的概念之一，是相似等概念的基础。笔者在平时的教学实践中，力求通过具体的教学活动，借助图形运动与演绎推理的有机结合，引导学生在活动中思考，在思考中体验，提升思维水平，更好地感受知识价值，获得“情感、态度、价值观”等方面体验的同时，凸显核心素养。

一、创设情境，引入概念

（多媒体展示一些全等图形的图片。）

师：观察这些图片，找一找它们共同的特征。

生1：形状一样。

生2：它们一样大。

生3：成轴对称。

师：同学们很聪明！确实，它们的形状和大小完全一样。你能再举出生活中的一些类似例子吗？

（师生活动，相互补充。）

设计意图：借助现实生活中实物的图片，让学生抽象出形状、大小完全一样的几何图形，在对周围环境直接感知的基础上生成新知识，建立形象直观的数学概念模型。

二、动手实践，生成概念

1.在实践活动中，动手感知全等三角形形状、大小的“定”。

师：请同学们在复写纸上画个三角形。因为我们用的是复写纸，所以我们可得到两个三角形。用剪刀剪下这两个三角形，观察它们有何关系？

（学生动手操作，对比，交流。）

师：请用语言归纳这两个三角形有何关系？

生4：它们大小相同，形状一样。

生5：两个图形能够重合。

师：再操作看看，用一个更贴切的词描述。

生（齐答）：是完全重合。

师：同学们太棒了！在数学中，我们把两个完全重合的三角形叫作全等三角形（教师展示全等的△ABC与△DEF）。在数学里，用符号“≌”表示全等，△ABC与△DEF是全等三角形，就记作“△ABC≌△DEF”，读作“△ABC全等于△DEF”。

2.在变化过程中，正确识别全等三角形对应元素的“等”。

师：那么，同学们再细心观察一下，全等的△ABC与△DEF各元素有何对应关系？

（学生以小组为单位进行观察。）

生6：我发现点A与点D，点B与点E，点C与点F重合。

生7：我发现边AB与边DE，边BC与边EF，边AC与边DF重合。

生8：我发现∠A与∠D，∠B与∠E，∠C与∠F 重合。

师：很好，同学们发现问题的能力都比较强。全等三角形有严格的对应关系，我们把对应重合的顶点称为对应顶点，对应相等的边称为对应边，对应相等的角称为对应角。

师：由此，我们可以知道两个三角形全等最显著的特点。

生（齐答）：对应相等。

师：太棒了！在数学中，为了清晰准确表示这样的对应“等”，你认为用“≌”符号书写时应该注意什么？

生9：一一对应，不能出错。

生10：对应着写。

生11：点的对应就是角的对应，也就是边的对应，要对应着写。

师：同学们讲得太好了！是的，必须对应着写，这样能直接看出对应相等的关系。这样的对应关系也体现了全等三角形对应相等的“唯一性”。

师：“≌”是全等符号，“∽”表示形状相同，“=”表示大小相等。利用全等符号，我们可以这样写出几何语言：

∵△ABC≌△DEF（已知），

∴AB=DE，BC=EF，AC=DF（全等三角形的對应边相等），

∠A=∠D，∠B=∠E，∠C=∠F（全等三角形的对应角相等）。

3.在互逆活动中，对比理解全等三角形本质特征的“动”。

师：请同学们拿出准备好的素材，自己动手进行图形的变换，并请思考三角形在平移、翻折、旋转变换的前后是否全等？

生12：都是全等的。

生13：三角形经过平移、翻折、旋转，位置变了，但形状、大小没变。

生14：三角形变换前后的图形是全等的。

师：同学们能说出它们的对应顶点、对应边和对应角吗？

（学生逐一回答。）

师：换一种思路，改变其中一个三角形的位置，怎么使它与另一个三角形重合？

生15：第一个图经过平移。

生16：第二个图经过翻折。

生17：第三个图经过旋转。

师：非常好！通过这两个互逆的活动，大家应该感受到了图形的运动可以帮助我们认识、理解几何图形。

设计意图：本环节是课堂教学的重点。笔者设计了3个层次的活动，力求让学生通过“画、剪、比对”，经历动手操作、观察实验、归纳等探究过程，深刻理解全等三角形的概念。第一层次，学生通过动手实践活动，直观感知全等三角形形状、大小的“定”，得到全等三角形的基本概念。第二层次，学生以小组为单位动手比对，找出全等三角形对应角、对应边相等的关系式，培养学生的语言表达和抽象思维能力，同时，教师规范几何语言的呈现，引导学生学会图形语言、文字语言、符号语言之间的互相转化。第三层次，学生在动手实践中体会三角形变换前后的“定”，会用图形运动去认识、理解几何图形，从而提升合情推理和简单演绎推理的能力。

三、启发尝试，应用概念

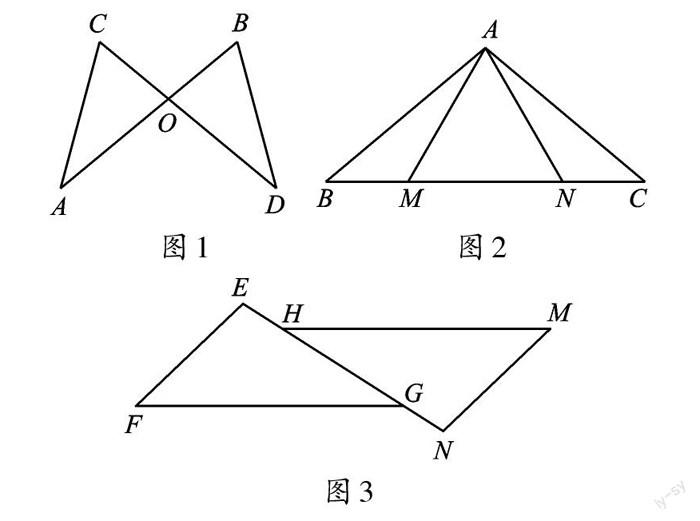
问题1：如图1，已知△OCA≌△OBD。你能找出对应相等的量吗？这两个三角形通过什么样的变换可以重合？

问题2：如图2，已知△ABN≌△ACM，若BM=10cm，则CN的长为________;若∠B=40°，则∠C的度数为 ________;若∠B=40°，∠MAC=80°，求∠ANB的度数。

问题3：如图3，若△EFG≌△NMH。

（1）FG与MH平行吗？为什么？

（2）求证：EH=NG。

师生一起分析解答。

设计意图：通过这组变式训练，强化学生对全等三角形概念的理解，培养学生初步运用全等三角形概念、性质解决问题的能力。3道题目隐含图形的运动，渗透利用图形运动解决几何问题的思想。通过变化两个全等三角形的位置，将全等三角形的概念、性质与相交线、平行线、三角形内角和等知识相结合，培养学生综合解题的能力。

四、课堂小结，强化概念

教师利用思维导图（图略），逐行呈现知识点。

设计意图：利用思维导图梳理所学内容，图文并茂地诠释全等三角形概念的内涵和外延。这样归纳，学生易于接受，也易于对知识点进行消化理解。

五、教学反思

1. 正确理解基本概念教学的三维目标。

概念教学之初，首要的是科学确定符合实际的三维目标。三维目标的三个维度相互交融，相互统一，都指向人的发展。所以，课堂教学首先关注的不是“学生要学什么”，而是“学完本节数学课，学生将获得什么发展”。基于此，在概念教学中，教师必须正确理解教学内容，以数学知识和技能为载体，制定恰当的三维教学目标。全等三角形是最基本的全等图形，对于其基本概念、性质的教学，笔者设计了基于生活情境的探究活动，制定了让学生厘清全等意义的“知识与技能”目标;引导学生边做边交流反思，制定了提升学生思维水平的“过程与方法”目标;考虑积极的情感、态度，制定了从生活升华至数学的“情感、态度与价值观”目标。这样的三维目标在课堂教学中发挥着真正的定向作用，效果跃然纸上。

2.注重设计基本概念教学的探究活动。

章建跃博士说过，“数学在根本上是玩概念的，只有围绕数学概念的核心展开教学，才能实现有效教学”。笔者的理解，这里的“玩”就是数学概念教学中探究活动的开展。在教学中，教师开展有效的探究活动，能够激发学生的学习兴趣和好奇心，而好奇心恰恰是构成核心素养的重要内容。学生在探究活动中获得愉快的体验，好奇心得到满足，培养了良好的学习品质，激发了求知动力，自然就能引发学生大胆进行探索活动，深化对概念的理解。本节课的教学，尽管知识点不多，也不难，但要让学生实现从具体到抽象，从感性上升到理性，有效的探究活动必不可少。教学一开始，笔者带领学生到生活中寻找全等图形，不断追问：“全等图形美不美？”“两个三角形全等与位置有关吗？”“全等三角形对应元素之間有什么关系？”“怎样运动来验证全等三角形的对应相等？”“全等三角形能帮助我们解决什么问题？”在一连串的追问下，学生通过亲手实践，厘清了概念，消解了困惑，拓展了思维。

3.重视渗透基本概念教学的内涵、外延。

学生对数学概念的掌握程度会受到许多因素的影响。在教学中，笔者力求让学生体验概念的形成过程，把概念放到相应的概念体系中，追本溯源，了解它的来龙去脉，不仅要知道学习这个概念需要什么样的基础，还要知道它以后能干什么，从而形成结构完整的概念体系。全等三角形的概念，是在前期学习了线段、角以及平行线的相关知识之后的内容，而后续全等三角形的判定方法、相似三角形、四边形的学习也是基于全等的概念展开的，这些概念之间存在一定的逻辑关系。讲解时，笔者有意识地借助图形的运动去帮助学生认识、理解几何图形，进一步夯实学生对线段、角、平行线的知识，为学生接下来识别复杂图形中的全等三角形以及四边形、圆提供有效的指引。

总而言之，在数学概念教学中，充分把握概念的本质，回归基本概念，积极创造条件，让学生在做中学，在学中做，多种感官协调统一，渗透数学思想方法，是“双减”背景下实施有效概念教学的根本途径。

（作者单位：江苏省泰州市姜堰区第四中学）