深度学习函数零点问题

江苏省张家港中等专业学校 周文国 215600

一般地，我们把函数y=f(x)的值为零的实数x称为函数y=f(x)的零点.需要注意的是：（1）函数的零点不是点，而是一个实数，当自变量取零点时，函数值为零.（2）函数y=f(x) 的零点就是方程f(x)=0 的实数根，即为函数y=f(x)的图象和x轴交点的横坐标.（3）要理解和把握零点存在定理，若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线，且f(a)f(b)＜0，则函数y=f(x)在区间(a,b)上有零点.因此函数零点存在性定理要求具备两个条件，一是函数在区间[a.b]上的图象是连续不断的一条曲线，二是需要注意f(a)f(b)＜0.

对于函数零点的常规题型是能求出函数的零点以及一元二次方程根的分布，但最典型的问题则为函数零点个数的确定和方程的根与图象间的关系.

1 用二分法解方程

例1 函数y=f(x)为定义在R 上的减函数，且为奇函数，解方程f(x3-x-1)+f(x2-1)=0（精确到0.1）.

分析：本题直接求解可能有点难度，但是通过二分法找出函数g(x)=x3+x2-x-2的零点，则可以很快解决.

解：由题意，y=f(x) 为奇函数，因此-f(x2-1)=f(1-x2)，原方程可以化为f(x3-x-1)=-f(x2-1)，即f(x3-x-1)=f(1-x2)，又函数y=f(x)为定义在R 上的减函数，∴方程可以化为x3-x-1=1-x2，即x3+x2-x-2=0.

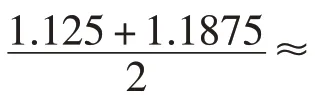
点评：结合二分法解方程的近似解，其关键是体会函数与方程的内在联系.

2 函数零点个数的确定

例2 求函数f(x)=2x| log0.3x|-1 的零点个数.

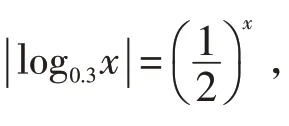
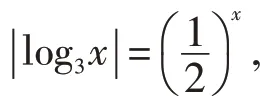
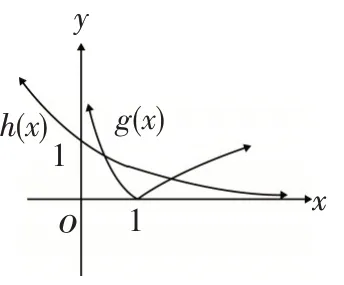
图1

3 已知函数零点个数求参数的取值范围

若关于x的方程f(x)=1 存在三个零点，则实数a的取值范围是______.

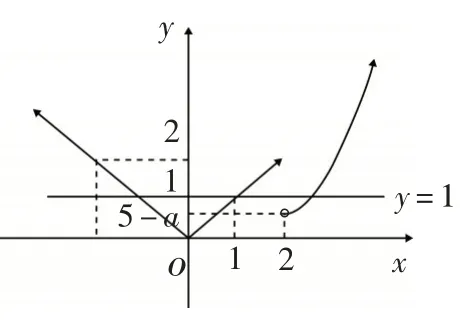
图2

点评：数形结合的方法是解决参数a的取值范围的重要节点.

4 函数零点范围的确定

例4 已知函数f(x)=-log2x的零点x0∈(n,n+1)(n∈N*),则n= ____.

解：由题意可知道，要求出函数f(x)=-log2x的零点即为方程=log2x的根，可设，可在同一坐标系中作出g(x)和h(x)的图象（如图3），结合图象可清晰知道x0∈(3,4) ，因此验证由x0∈(3,4)，则n=3.

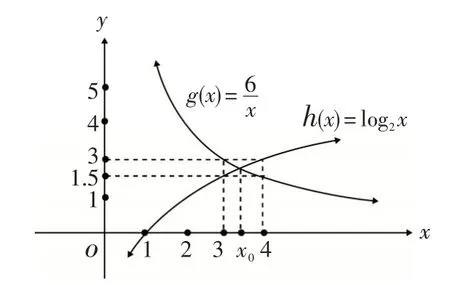
图3

5 最值问题

例5 已知函数f(x)=x2+ax+b在区间[0,1]内存在零点，求ab的最大值.

分析：设一个零点x0，可将ab转化为x0的一元二次函数求解.