内河航道网络优化研究
王 伟,刘弘昱,胡海宇,蒋 磊,黄 莉
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098; 2.南通河海大学海洋与近海工程研究院,江苏 南通 226004;3.中交第二航务工程局有限公司,湖北 武汉 430000;4.河海大学公共管理学院,江苏 南京 211100)
自新旧动能转换战略实施以来,淘汰落后产能,优化产业布局,内河水运规划建设的内外部环境发生了一些新的变化。经济结构的转型升级对内河水运的发展也提出了新的要求,优化内河航道网络,对构建综合运输体系、保障内河水系可持续发展、促进社会经济快速发展等都具有重要意义。
优化问题求解常用的方法有改进型遗传算法[1]、遗传-剩余矩形算法[2]等,航道网络的优化能够高效率地发挥江海河联运的功能。已有学者[3-8]对航道网络优化进行了研究,建立了内河航运网络优化模型,并利用Dijkstra算法[3]、仿真方法[4-6]、Frank-Wolfe法[7]、遗传算法[8]等得到航道网络优化方案,通过实例验证了模型的有效性。也有学者探讨了航道网络优化的规模及等级,潘静静等[9]建立了网络配流优化模型进行网络节点的最优配流,优化了航道网络的服务质量;胡晓红等[10-11]运用数据分析方法优化提升航道网络规模;徐力等[12]通过改进航道通过能力模型为航道优化提供参考;Huang等[13]基于原始法和对偶法建立内河航道网模型为航道网的管理、规划提出了建议。
在对航道网络方案进行优选评价方面,余佳等[14]采用直觉模糊熵权幂平均方法选取最终方案。李文杰等[15-18]提出以航道承载力作为评价指标,分析航道客观条件,利用聚类分析法建立航道网络规划方案优选模型,以此来解决航道网络规划方案的优选和评价问题。同为交通网络,水运网络可与陆路交通网络进行类比借鉴,Lebedeva等[19]应用Voronoi模型优化城区交通枢纽服务区和物流中心货物配送路径;黄肖玲等[20]建立了钢铁产成品运输网络优化模型并运用粒子群算法有效降低了运输网络的总成本。
综合来看,国内外对于内河航道网络优化的定量化研究较为缺乏,而航道网络优化过程大多忽略了交通运输网络利益相关者对于航道网络优化的影响。相比而言,丰富的传统交通运输网络优化研究对航道网络研究有较大的借鉴意义,本文运用交通运输网络优化问题中的双层规划模型对内河航道网络优化进行研究,构建内河航道网络特征的网络优化模型。
1 问 题 提 出
传统交通运输网络优化问题主要分为离散性网络优化问题和连续性网络优化问题,离散性网络优化是指在航道网络中确定需要新通航航道,连续性网络优化是指在航道网络中确定现有航道应提升的通航能力幅度。
航道网络优化问题实际上是一个博弈问题,是货主、航运企业与航道网络规划者之间的博弈。航道网络规划者从系统的角度对网络制定相关决策来改变货主和航运企业的路径选择,从而达到降低整个航道网络系统总出行费用或总出行时间的目的;货主和航运企业从自身角度进行最优选择,他们的选择又会影响航道网络规划者的布局,三者之间互相影响,直到航道网络系统达到均衡,此时的航道网络即为系统最优方案。
目前,多数地区内河水运发展存在发展速度慢、结构不合理、分布凌乱、集约化程度不高、港城关系协调度低、管理体制落后、发展思路跟不上等问题。因此,需要构建一个双层规划模型来解决内河航道网络优化问题,即在满足水运需求的前提下,使航道网络优化方案的建设成本和运行成本最小,同时明确网络中现有航道的等级提升以及航道网络中新通航航道的新建等级。
2 内河航道网络优化模型构建及其求解
2.1 模型假设
为简化内河航道网络优化问题,建立内河航道网络优化模型时假设:①内河航道网络中产生的货运量都能得到运输;②船舶出行在起讫点之间会选择出行时间最短的路径;③不同等级航道上的运输船舶均为该航道通行的标准船舶;④内河航道通航td/a,1天的通航时间为Th;⑤船舶的航行速度v已知且恒定不变;⑥现有航道的等级不存在降低的可能。
2.2 航道网络优化双层规划模型构建
2.2.1 上层模型——航道网络优化模型
2.2.1.1 目标函数
目标函数为
(1)
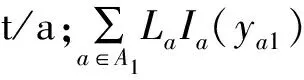
2.2.1.2 约束条件
上层模型约束条件中,式(2)表示各航道货运量不超过其实际通行能力;式(3)表示现有航道优化后的等级不低于现状航道等级;式(4)表示新通航航道等级的取值范围:
0≤xa≤Qa∀a∈A
(2)
ya1∈{ya1,0,ya1,0-1,ya1,0-2,…,0}
(3)
ya2∈{0,1,2,…,7}
(4)
式中:Qa为航道a的实际通行能力,万t/a;ya1,0为现有等级航道的现有等级。
2.2.2 下层模型——航道网络配流模型
2.2.2.1 目标函数
在航道网络配流过程中,航道网络中的货主和航运企业是否明确了解各航道的出行时间将大大影响航道网络配流模型的构建。下层选择构建基于用户均衡的单模式航道网络配流模型:
(5)
式中:Z(x)为用户均衡下的目标函数;μ为相对权重;ta(xa)为航道a上交通量为xa时的航行时间,h;Pa为船舶在航道a上航行的通行费用,元;G为时间价值。
2.2.2.2 约束条件
下层模型约束条件中,式(6)(7)分别表示航行时间及船舶通行费;式(8)表示需求约束;式(9)表示路径流量与航道流量之间的关系;式(10)表示非负约束;式(11)表示航道a的交通量不超过其实际通行能力:
(6)
Pa=γnaDya
(7)
(8)
(9)
fij,k≥0 ∀k∈R(i,j)∀i,j∈N
(10)
0≤xa≤Qa∀a∈A
(11)
式中:ta,0为航道a上交通量为0时的航行时间,h;α、β为待定参数;γ为船闸收费标准,元/(t·次);na为航道a上船闸的数量;Dya为等级为y的航道a上标准船舶载重,t;N为航道网络中所有节点的集合;R(i,j)为OD(交通出行量,Origin and Destination)对(i,j)的所有路径集合;fij,k为第k条路径上的流量,万t/a;qij为OD对(i,j)之间的货运需求,万t/a;σij,a,k为路径与航道的关联关系,当航道a在连接OD对(i,j)的第k条路径时其取值1,否则为0。
2.3 模型求解
遗传算法在解决双层规划模型问题中运用广泛,收敛速度较快,求解精度也较高,在搜索过程中能够跳出局部最优从而较好地得到全局最优解,因此选用遗传算法求解该航道网络优化双层规划模型,求解步骤如下。
a.根据内河航道网络现状结构、规划年货运量总OD表以及内河航道目前在建工程等因素确定所有可能连接边,即生成一个初始可能连接图,作为问题的初代解。设航道网络中现有航道数为n1,新通航航道数为n2,则染色体编码{ya1,1,ya1,2,…,ya1,n1,ya2,1,ya2,2,…,ya2,n2}能够表示一个航道网络的优化方案。
b.设定初始进化代数Gen=0,最优值维持步长stop=0,令初始目标值Cmax为非常大的正数,对各个体对应的目标函数值(航道网络优化方案的建设成本和运行成本之和)进行排序并与当前最优值进行比较,将不大于当前最优值的目标个体代入下层航道网络配流模型中,计算各航道的货运量。
c.若进化代数(Gen)大于最大进化代数或最优值维持步长(stop)大于收敛判断步长,转到步骤g,否则,令Gen=Gen+1,转到下一步。
d.根据下层模型中航道网络配流的结果检验是否满足上层模型的约束条件,给不满足约束的航道加上惩罚值(可为航道运行成本与建设成本之和的倍数)。航道网络优化方案的运行成本、建设成本与惩罚项一起构成总的目标函数值,产生个体最优目标值Z1和最差目标值Z2。
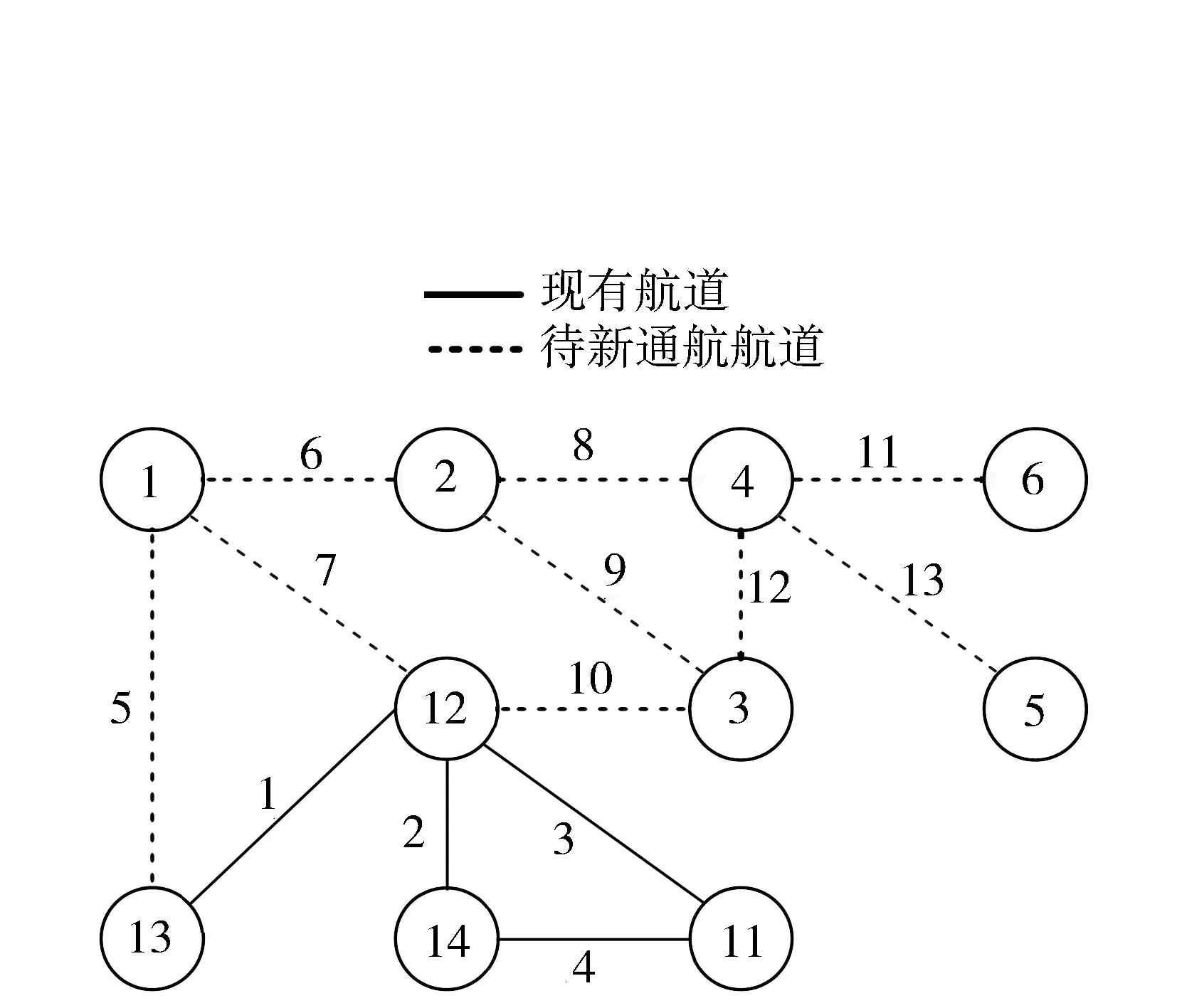
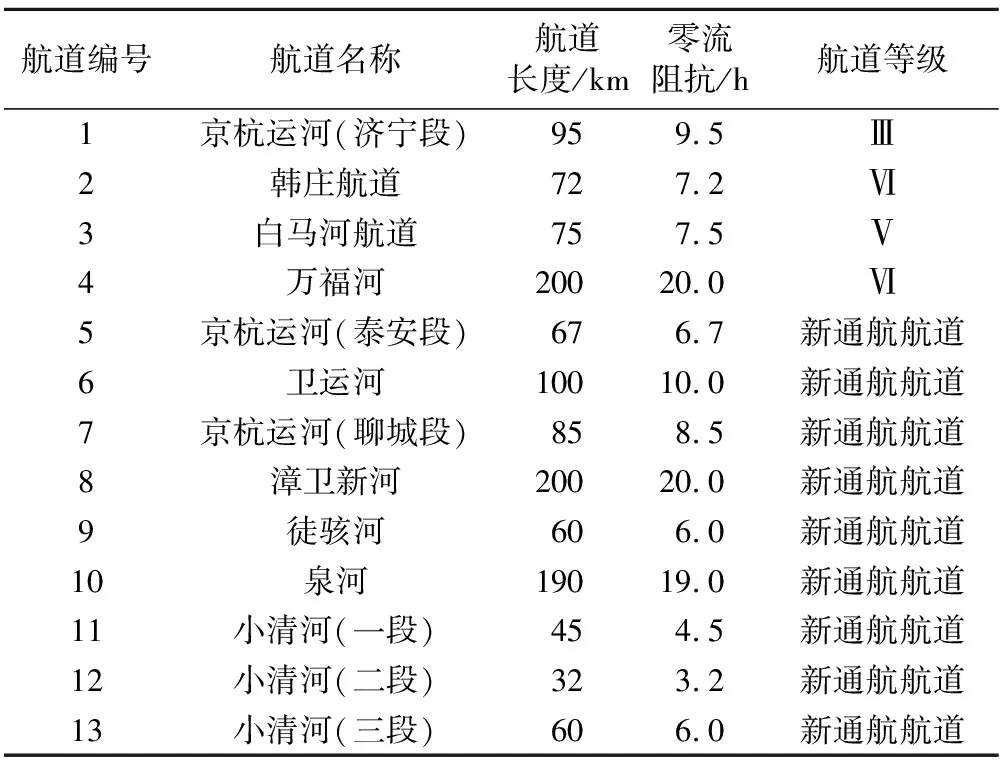
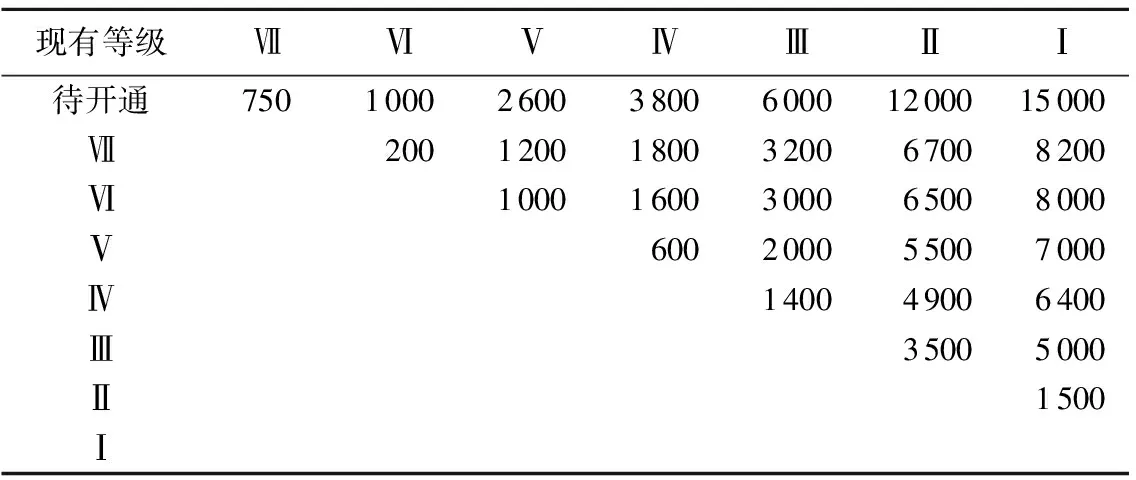
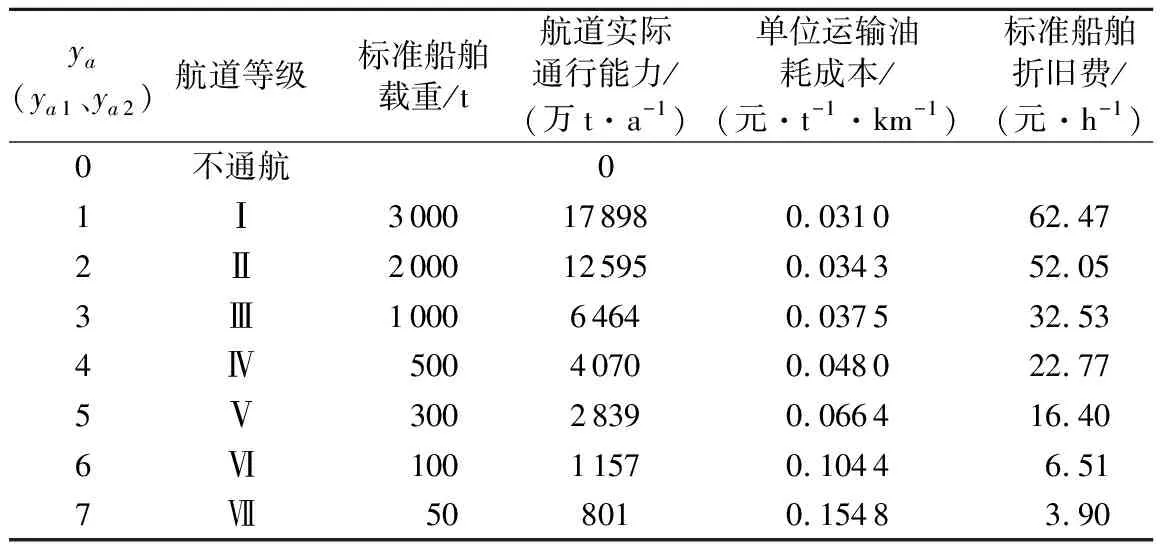
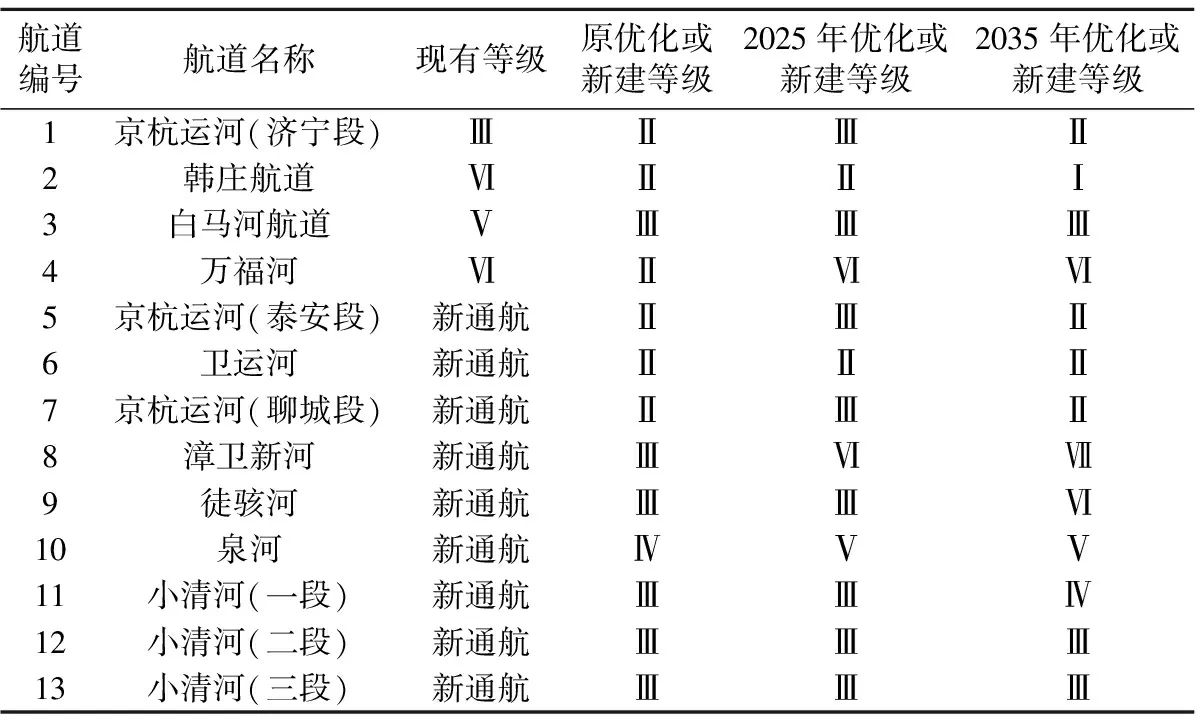
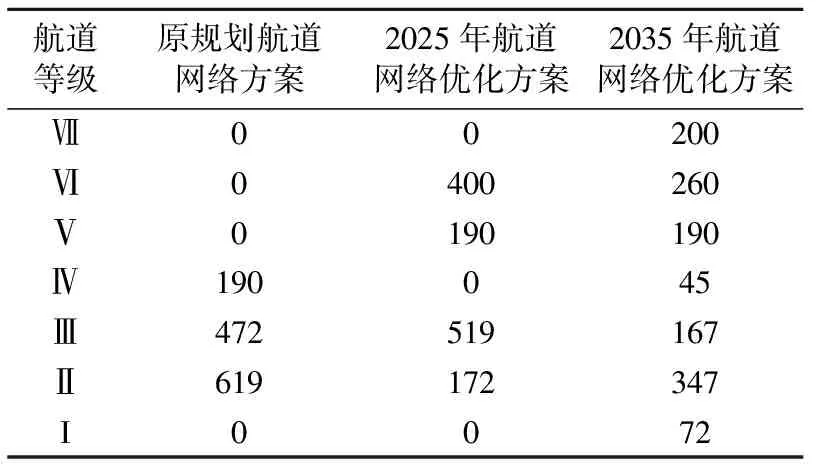
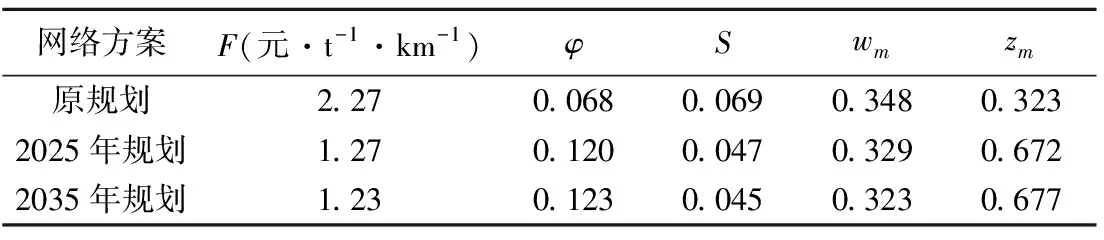
e.计算未参与下层模型航道网络配流个体的上层目标函数值与参与了下层模型航道网络配流个体的上层目标函数值最大值的比θ,其目标函数值为θZ2,若Z1 f.以上层模型中的目标函数作为适应度函数,运用轮盘法对染色体进行选择、交叉、变异操作,转到步骤c。 g.输出结果,得出最优的内河航道网络优化方案。 近年来,山东省内河水运迎来了黄金发展期,高等级航道建设持续提速,但仍然存在如航运服务水平低、航道网络布局不足等问题。根据《山东省统计年鉴(2019)》,山东省水路运输货运量占总货运量的5.14%。山东省内河航道通航里程1 239.9 km,主要集中在鲁西南济宁、枣庄、菏泽等地区,但Ⅲ级及以上航道仅355.6 km,占山东省内河航道的28.7%;京杭运河支线航道等级偏低,尚未建成干支通达的高等级航道网。 根据山东省内河航道网络的特点,在山东省内河航道网络中选择16个节点,见表1。 表1 航道网络节点编号 未来随着山东省小清河航道、大清河航道、梁济运河航道、新万福河航道、京杭运河湖西航道、京杭运河济宁至台儿庄扩建(济宁段)和京杭运河(枣庄段)扩建工程等航道的通航,济南市、淄博市、滨州市、东营市等都将产生内河货运量。据此通过四阶段法预测可得山东省内河航道网络未来特征年货运量总OD表,见表2、表3。 表2 未来特征年(2025年)货运量总OD 根据《山东省内河航道与港口布局规划(2020—2050年)研究报告》(以下简称原规划)中未来山东省内河航道的规划建设方案以及航道在建工程,选择9条在山东省内河航道网络中起着重要连通作用的航道,作为此次航道网络优化中的备选新通航航道,结合山东省现有的4条内河航道,形成山东省内河航道网络优化涉及的所有航道,航道信息见表4。 由表2、表3、表4可以看出,节点7、8、9、10、15、16并没有现有航道或待通航航道连通,最终山东省内河航道实际网络图可抽象为拥有10个节点、4条现有航道、9条新通航航道的航道网络,则山东省内河航道网络初始可能连接图见图1。 表3 未来特征年(2035年)货运量总OD 图1 航道网络初始可能连接Fig.1 Initial possible connection diagram of waterway network 表4 内河航道网络各航道属性 因地理位置与环境的不同,航道升级或新建其单位造价也会随之变化。对山东省类似内河航道项目的建设投资进行分析统计,确定山东省内河航道网络中现有航道提升等级所需的单位造价,如表5所示。 表5 现有等级航道升级单位造价 将航道等级进行编号,航道等级及其对应信息见表6。其他参数取值α=0.15;β=4;交通系统γ=0.6元/(t·次),水利系统γ=1.2元/(t·次);μ=1;λ1=0;λ2=1。 表6 决策变量及对应值 使用MATLAB进行编程求解,将原规划的优化结果与模型的优化结果进行对比,结果见表7。各等级航道总里程见表8。 表7 山东省内河航道网络优化结果 从表8可看出,仅有小部分航道网络优化结果与原规划结果相差较大,其中万福河连接菏泽和枣庄两市,但这两市间的货运量也可通过白马河航道及韩庄航道进行运输,且实际运输效率更高,故万福河优化等级维持现有等级;京杭运河(泰安段)连接泰安和聊城两市,但这两市间的货运量也可通过京杭运河(济宁段)及京杭运河(聊城段)进行运输,且实际运输效率更高,故京杭运河(泰安段)只需承担很少部分的货运量,则模型求解得到新通航道等级较低。但由于《山东省内河航道与港口布局规划(2020—2050年)研究报告》中京杭运河山东段规划为Ⅱ级,与模型求解结果相差较大,所以决定令京杭运河(泰安段)新通航道等级与京杭运河(济宁段)和京杭运河(聊城段)一致,在2025年新通航道均为Ⅲ级,2035年新通航道均为Ⅱ级。 表8 各等级航道总里程 为了更深入地验证该航道网络优化双层规划模型结果的优越性,选择航道网络总单位运行成本、航道网络整体利用率、当量等级航道密度[18]3个评价指标对该内河航道网络方案进行评价。 a.航道网络总单位运行成本F: 式中r为折算利率,取2020年中国人民银行定期存款年利率,即r=1.5%。 b.航道网络整体利用率φ: (13) c.当量等级航道密度S: (14) 式中:Hy为等级为y的航道总里程,具体取值见表8;By为等级为y的航道换算系数,根据山东省内河各等级航道技术状况及其通过能力的大小,其不同等级航道换算系数从Ⅰ级至Ⅶ级分别为10.0、9.2、8.1、7.3、4.4、2.2、1.0。 d.方案评选公式为 J′wT=(z1,z2…,zm) (15) 其中w=(w1,w2,…,wm) 式中:J′为决策矩阵J=(F,φ,S)的标准化矩阵;wT为评价指标的权重,根据专家评分法确定。 通过式(12)~(15)得到评价指标计算结果,见表9所示。 表9 各网络方案评价指标结果 根据表9可知,2025年0.672>0.323,2035年0.677>0.323,说明不论是模型求解得出的2025年航道网络优化方案,还是2035年航道网络优化方案,均比原规划的航道网络方案更加优越,验证了该内河航道网络双层规划模型的可行性。 本文在考虑货主、航运企业与航道网络规划者之间博弈关系的基础上,构建了以航道网络优化方案的建设成本和运行成本之和最小为上层,基于用户均衡的航道网络配流模型为下层的航道网络优化双层规划模型。算例结果表明,本文方案优于原规划方案,设计的双层规划模型切实可行。但本文在计算上层模型时将决策变量离散化为航道等级,难以具体地反映网络中航道的优化程度,若能够采用连续性决策变量,再对求解结果进行具体分析,将使得航道网络的优化方案更加贴合实际情况。3 实 证 分 析
3.1 数据整理
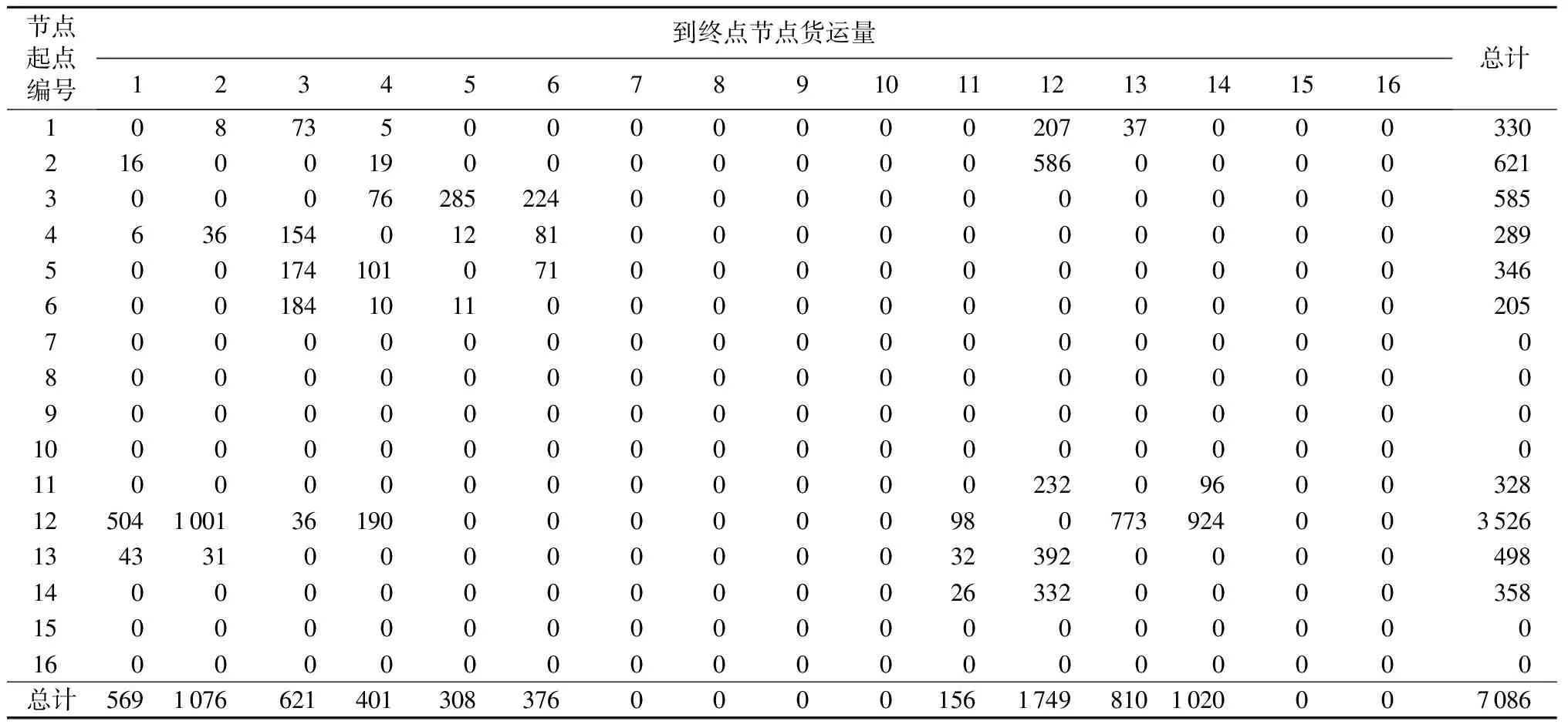
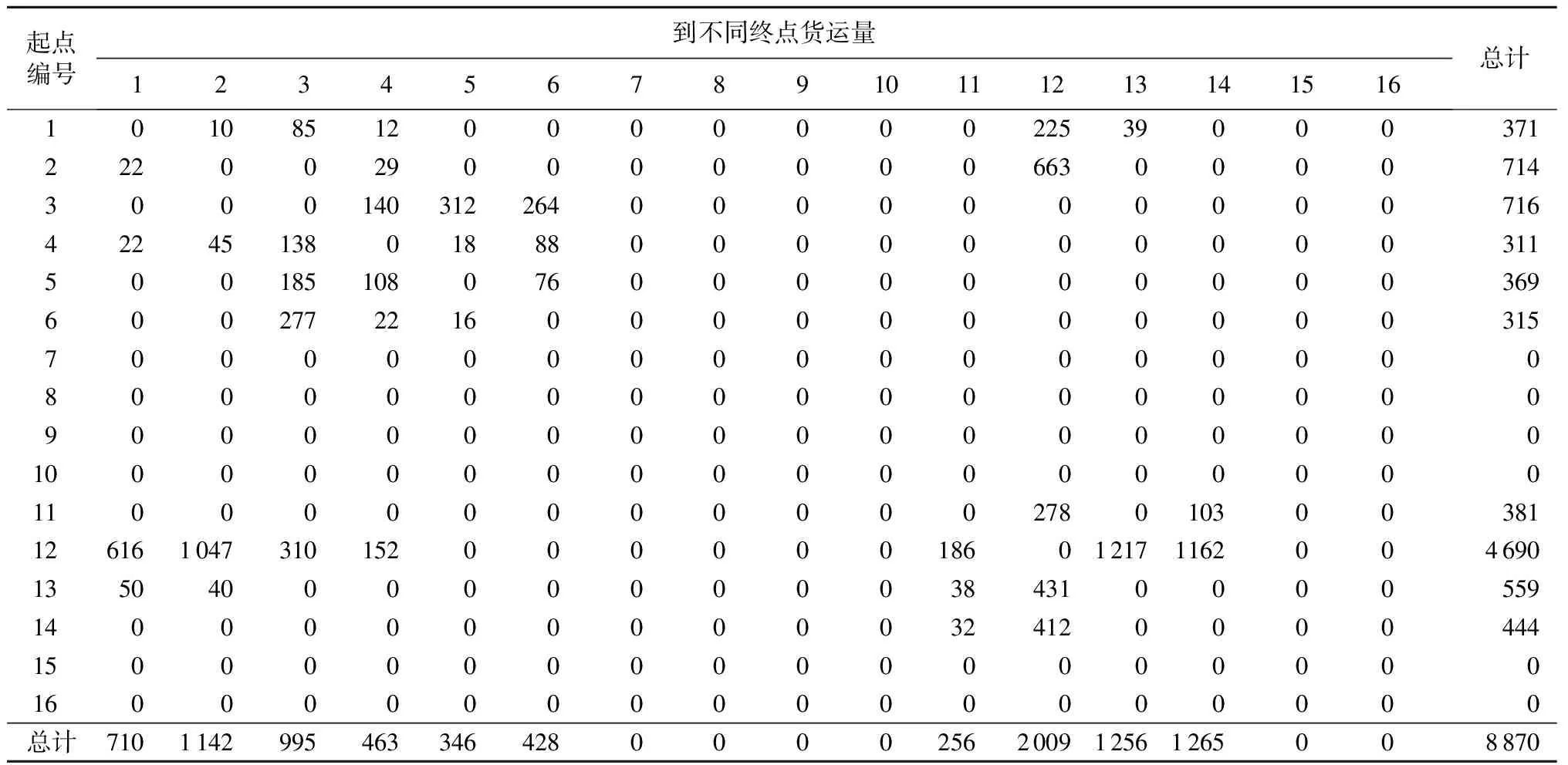
3.2 结果分析
4 结 语

