一种面向最小能耗自适应汇聚路由判定算法
孙泽宇,兰 岚,曾 操,廖桂生
(1.西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071;2.洛阳理工学院 计算机与信息工程学院,河南 洛阳 471023;3.西安电子科技大学 信息感知协同创新中心,陕西 西安 710071)
无线传感器网络通过自组织方式将大量的传感器节点连接成大规模的网络系统[1-3]。该网络系统具有较强的适应性和鲁棒性,传感器节点之间可以通过无线方式进行数据传输与通信,以协同方式完成对某种特定事件的监测[4-5]。传感器节点虽然具有一定的通信能力、计算能力、存储能力和感知能力,但其能力范围有限,极易受外部环境、自然因素等方面制约,如电能无法补充、通信链路拥塞等[6-8]。在传统的数据传输阶段,主要是依靠传感器节点将数据上传到Sink节点后,再进行数据融合和计算,其不足主要体现在两个方面:(1) 传输效率低。由于大量传感器节点同时向Sink节点发送数据,必然要在信道内产生大量的冗余数据,增加了数据延时时间,造成了数据冲突与碰撞,降低了数据传输效率。(2) 网络能耗增加。无线传感器网络在节点部署阶段采用密集型部署方式,导致节点之间相邻区域出现大面积的重叠区间,故节点在发送与接收数据时无故地消耗了大量网络能量,造成了节点能量快速消耗与节点失效,缩短了网络生存周期。因此,如何更好地提高可靠性数据传输效率和节约网络能量,已成为无线传感器网络目前研究的主要问题。
近些年,国内外诸多专家学者对无线传感器网络的节能问题和可靠性数据传输做了大量研究工作。文献[9]通过路由链表完成路径选择过程,其算法是将目标节点位置信息和当前节点的下一跳节点的路由写入路由链表。当数据在传至下一跳节点时,更新路由链表下一跳的节点信息,以保证传输数据的可靠性。文献[10]中提出一种自适应的分层路由协议,可以减少参与路由计算的节点数量,缩减路由表长度,降低了交换路由信息所需能量的开销,利用分簇机制形成了较稳定的子图网络,减少了网络拓扑变化,延长了网络生存周期。文献[11]中提出了一种基于数据为中心的路由选择算法,以节点到Sink节点之间的距离进行分类,确定不同类别的优先权;不同类别的节点在单位时间内向Sink节点发送数据;当所有不同类别的节点完成本轮任务后,再继续下一轮操作。该算法避免了数据冲突与碰撞,减少了数据冗余,提高了数据传输效率。文献[12]提出了一种基于凸壳的快速聚合规划策略(Quick Convex Hull-Based Rendezvous Planning,QCHBRP),以实现不相交的无线传感器网络的完全连通,并构建移动汇聚的短路径。一方面,该策略可以通过移动Sink节点,快速地在监测区域内寻找多个数据“聚合点”,用以完成不相交区域的互连互通;另一方面,QCHBRP策略将整个网络划分为多个子网络,并保证每个子网之间的距离近似相等或小于距离阈值;利用子网中的簇首节点转发数据至Sink节点,从而规划了从子网至Sink节点之间的路径。文献[13]中提出了一种基于压缩感知丢包匹配数据收集算法(packet loss Matching Data Gathering Algorithm based on Compressive Sensing,CS-MDGA),通过压缩感知技术构建了全网节点的“关联效应”,分析了树状路由在严重丢包情况下的重构精度,证明观测矩阵近似于“1”时的等距约束条件,最后给出了多路径备份路由传输机制。文献[14]中提出了一种基于压缩感知的聚类联合环形路由数据收集方案(Compressive Sensing Clustering joint Annular Routing Data Gathering scheme,CS-CARDG),采用集群采集数据方法完成数据传输过程。首先,对全网进行分簇,利用压缩感知技术将簇成员节点所采集到的数据构成多维数据包,发送给簇首节点。当簇首节点将多维数据路由到Sink时,CS-CARDG方案将会从最外环开始,由外到内依次压缩相同的分形数据,并通过最短路径路由到基站。
上述研究虽然在一定程度上优化了路由选择过程,但由于忽视了全网能量以及数据融合等因素,将会导致数据在传输和聚合时,网络能量消耗较大,数据融合效率降低,网络延时增加以及网络生存周期缩短等不足。针对上述问题,笔者提出了一种面向最小能耗自适应汇聚路由判定算法(Adaptive Sink-routing Decision algorithm for Minimum-energy Consumption,ASD-MC)。ASD-MC算法利用节点之间的欧氏距离相关系数给出了汇聚增益表达方法以及数据融合度与能量开销的函数关系;计算了数据融合度介于最小值和最大值之间时,与距离相关参数之间的比例关系;利用数据压缩能耗比函数关系,证明了两类不同节点提供可靠性传输距离满足的必要条件,从而确定了数据传输最优路径,达到了优化汇聚路由的目的。
1 问题描述
1.1 网络模型
文中的网络模型借助于图论理论中图的概念加以表示,即G=(V,E),其中V表示所有传感器节点集合,E表示任意两个节点之间所有可能传输数据的链路集合[15]。可以把整个网络的路由搜索空间减少到由多个子簇所形成的子网。在簇内,只有簇首节点可以主动维护网络的路由信息,簇成员节点不参与路由维护过程,从而减少了路由更新的开销。当没有数据发送时,簇成员节点转休眠状态,这样就保证网络在正常连通条件下,减少转发节点的数目和数据传输总量,降低拥塞和干扰发生的概率。为了更好地解决问题,笔者做如下规定:(1) 在全网内,任意节点都可以完成数据汇聚任务,把所有数据汇聚成一个数据包。(2) 簇内或簇间节点接收到相邻节点发送的数据后,将自身数据与接收数据进行融合,并把融合后的数据作为新数据传送给下一跳节点,直至把最终数据发送给Sink节点。
融合后的数据量应不大于节点m和节点n的原始数据量之和,不小于节点m和节点n中的任意节点的原始数据:
max{g0(m),g0(n)}≤g1(n)≤g0(m)+g0(n) ,
(1)
其中,g0(m)和g0(n)表示数据融合前的数据量;g1(n)表示数据在节点n处融合后的数据量。
能量模型采用Heinzelman提出的自由空间和多路衰减模型。当传输距离d小于距离阈值d0时,路径损耗指数为2;当传输距离d大于或等于距离阈值d0时,路径损耗指数为4,则能量模型数学定义为[16]
(2)
(3)
其中,ETx表示发射模块消耗的能耗;ERx表示接收模块消耗的能耗;Eelec表示发送或接收1 bit数据量时所消耗的能量;Efu表示节点进行融合时所消耗的能量;Zdata_pa表示融合数据包的总量;Eda表示融合1 bit数据量所消耗的能量;k表示发送或接收的数据量;εfs,εmp是功率放大时的能耗系数。
1.2 汇聚增益模型
在无线传感器网络中,传感器节点应根据数据汇聚增益自适应地调节数据融合位置信息,这样才能更好地抑制能量消耗。用cmn表示数据融合度,表示在节点n处融合后数据量g1(n)较融合前数据量[g0(m)+g0(n)]减少了cmn,其数学模型为
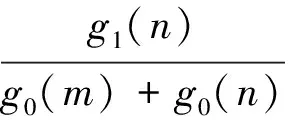
(4)
感知数据从源节点传至Sink节点时,路径上单位数据能量开销记作E(n,S),任意节点在进行数据融合时能量开销记作q(e)。根据式(4),得到汇聚增益Δ(m,n)为
Δ(m,n)=[g0(m)+g0(n)][E(n,S)-(1-cmn)E(n,S)+q(e)] 。
(5)
当传感器节点通信半径为感知半径的2倍时,记作Rc=2Rs。当任意两节点之间欧氏距离do大于Rc时,则两个节点之间相关参数为0;当任意两节点之间欧氏距离d小于或等于Rc时,则两个节点之间的相关参数为τ,数学表示式为
(6)
2 解决方案
2.1 融合度分析
基于对汇聚增益模型的分析,节点m和n之间的距离相关参数为τ且不等于0,则在节点n汇聚后,其汇聚后的数据量可表示为
g1(n)=max[g0(m),g0(n)]+min[g0(m),g0(n)](1-τ) 。
(7)
根据式(5)和式(7),可得数据汇聚后的增益为
Δ(m,n)=[g0(m)+g0(n)][E(n,S)-q(e)]-
max[g0(m),g0(n)]+min[g0(m),g0(n)](1-τ)E(n,S) 。
(8)
如图1所示,如果节点n的子节点只有一个节点m,则可以通过式(7)直接计算汇聚增益。
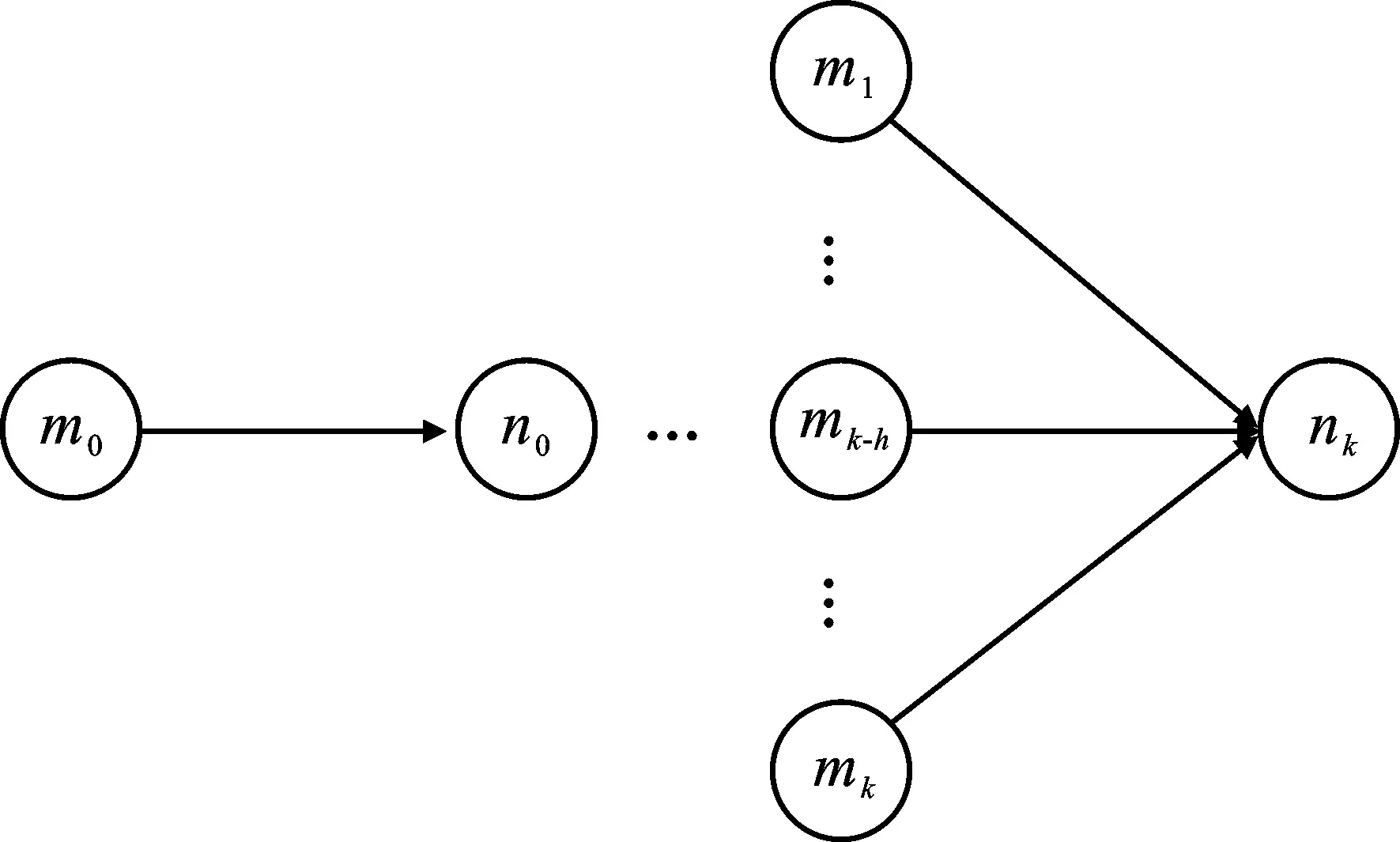
图1 单节点与多节点数据传输链路图
当节点n存在多个子节点时,则汇聚增益数学表达式为
Δ(m1,m2,…,mk,nk)=[g0(m1)+g0(m2)+…+g0(mk)]-
{E(n,S)-[(1-c(m1,m2,…,mk,nk))E(n,S)+q(e)]} 。
(9)
当汇聚增益大于0时,化简式(9),可得
(10)
当数据融合度满足式(10),数据在任意节点处进行融合时:
(11)
当数据融合度满足式(11)时,节点将数据直接上传给Sink节点,不需要进行汇聚处理。由于节点之间对数据融合能力存在一定差异,因此令cmin为数据融合度最小值,cmax为数据融合度最大值。
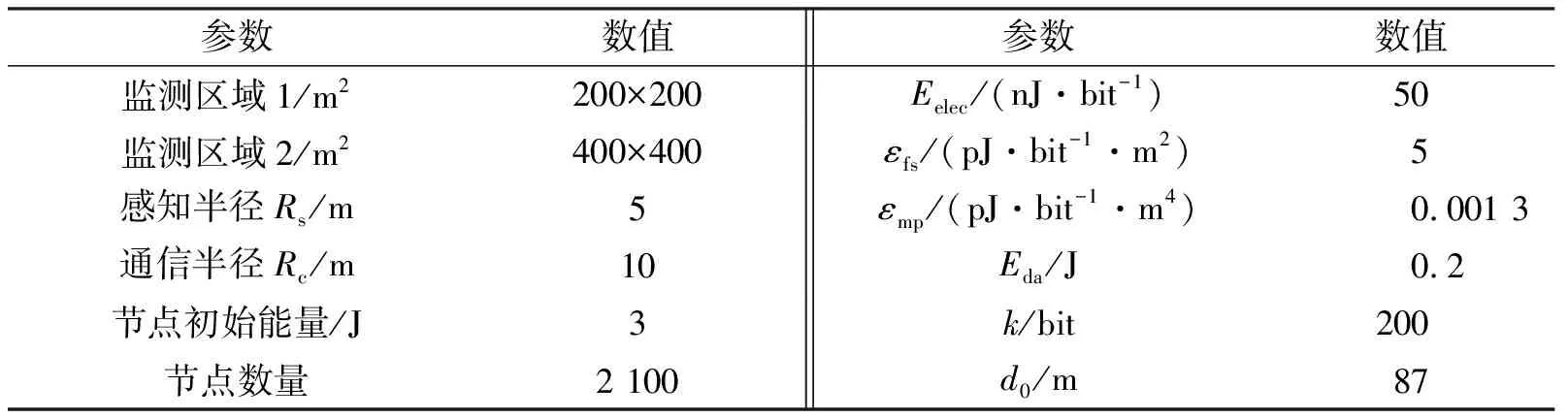
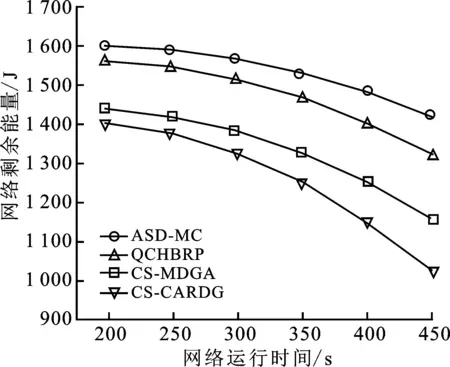
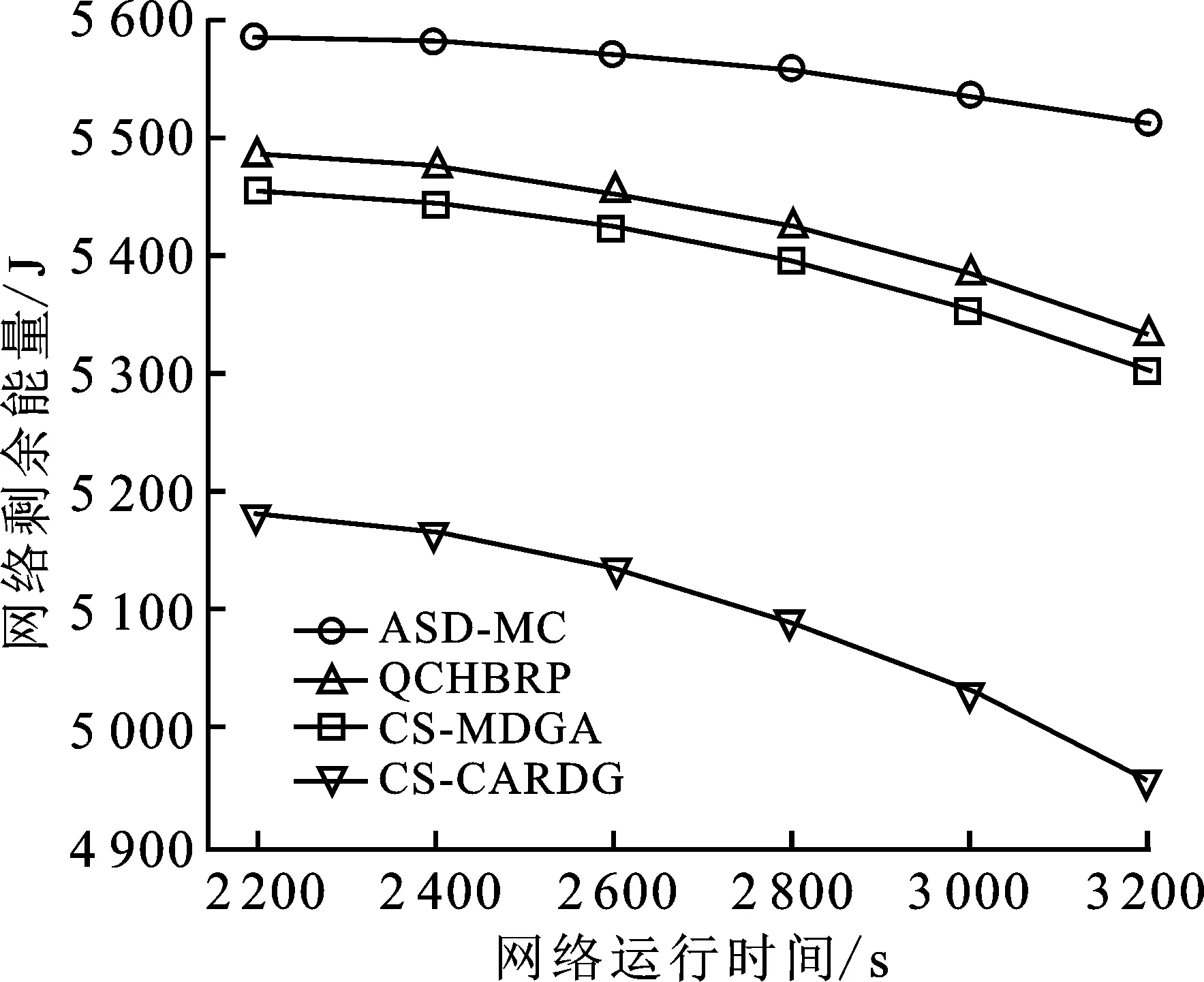
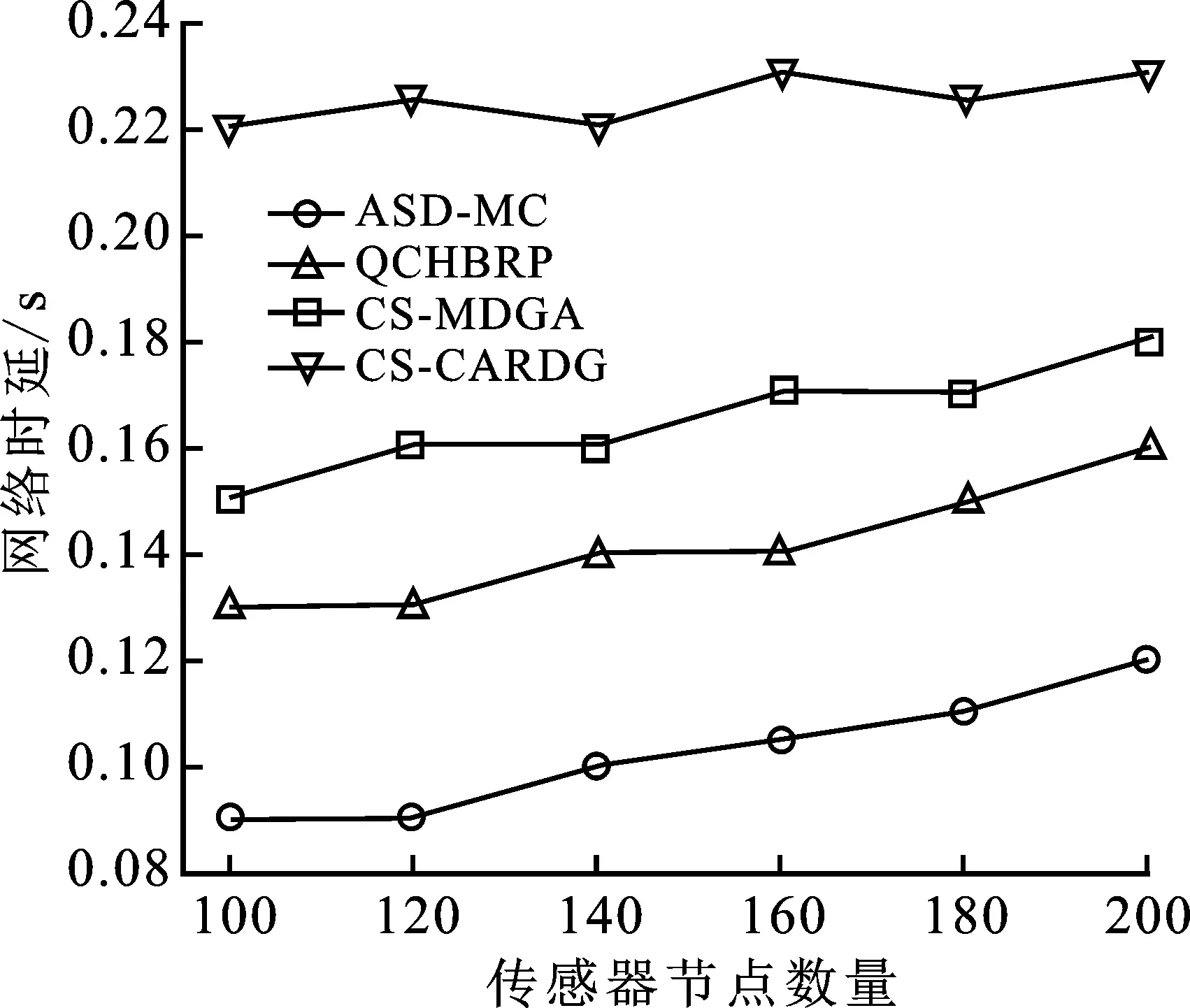
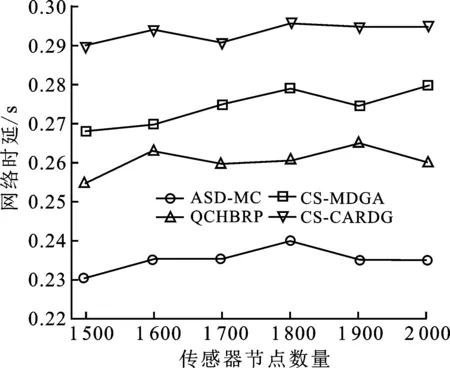
讨论1当cmin max[g0(m),g0(n)]+min[g0(m),g0(n)](1-τ)=(1-cmn)[g0(m)+g0(n)] 。 (12) 计算cmn,可得 (13) 由式(13)可得,数据融合度与距离相关参数成正比。由式(6)可得,当τ=0时,说明两个节点为正切状态;当τ<0时,说明两个节点为相离状态;当τ>0时,说明两个节点为相交状态。因此,在满足式(10)和式(11)时,可以自适应地判断出节点是否进行汇聚操作。对于cmin (14) 利用式(13)和式(14)分别计算出数据融合度和距离相关系数后,对原始子节点n1,n2,…,nk进行迭代更新操作,直至迭代更新所有子节点后,判断此时数据融合度是否满足式(10)。如果满足式(10),则进行汇聚融合操作;如果不满足,则不进行汇聚操作。 定理1多节点在进行数据传输时,如果没有在下一跳节点进行融合,那么在后继节点中,也不会再进行数据融合处理。 证明 现以图2为例进行说明。 图2 多节点数据传输链路图 除根节点之外的节点分为两类:第1类节点是沿最短路径将数据信息发送给Sink节点,不考虑汇聚增益;第2类节点则是根据汇聚增益判断是否进行汇聚处理。设节点集合为M,mi∈M。由于数据并没有在节点n0处进行融合操作,所以在节点n0处汇聚增益应小于零,即 c(m1,m2,…,mk,nk)E(n0,nk)≤q(e) 。 (15) mk作为n0的下一跳节点,距目的节点mk的距离长度要小于n0,故E(mk,nk) c(m1,m2,…,mk,nk)≤c(m1,m2,…,mk,n0) 。 (16) 由此类推,下一跳汇聚节点的数据融合度均小于或等于上一跳节点的数据融合度。因为最外层节点n0尚未进行数据融合,而其他节点的融合度又小于或等于n0融合度。因此,其他节点也不会进行数据融合操作。此时,两个节点的欧氏距离大于或等于Rc时,数据传输过程只能采用多跳方式将数据信息传至Sink节点。 证明完毕。 数据在无线传感器网络进行融合操作时,往往伴随着数据压缩,如数据信息为图像、音频、视频等[17-18]。当传感器节点采集数据量较大,又在某节点进行数据融合时,其压缩能耗不能忽略。这是因为数据在压缩和解压过程中会消耗较多的节点能量。为了方便地研究问题,笔者认为数据压缩时所消耗的能量与数据解压时所消耗的能量相等,即Eco=Ede,压缩比定义为γ。基于节2.1的分析可以看出,在数据传输过程中采用两种方式进行传输:第1种方式先汇聚后传输,即数据按照路由规划将数据传输给下一跳节点并进行数据融合,在后继传输过程中,按照前面的处理继续此操作;第2种方式是数据按照路由规划的最优路径将数据以多跳形式直接发送给Sink节点。在此过程中,不需要做数据融合处理。 讨论2数据在传输过程中,首先要在源节点做压缩操作,而后将压缩后的数据传输给下一跳节点;当下一跳节点接收到该数据包时要先做解压操作,再进行融合操作。当数据发送与接收时所消耗的能量大于压缩与解压的能量时,此压缩与解压操作是有效的;否则是无效的。当压缩与解压处于无效时,数据信息不会在下一跳节点进行汇聚,而是将数据以多跳形式直接传输给Sink节点。假设从源节点到Sink节点存在N个节点,当数据信息从节点m传至节点n时,根据式(2)和式(3)计算网络能耗为 (17) 其中,di表示节点i到相邻节点之间的距离。 当数据信息在节点m处进行压缩,在n处进行解压时,此时网络能耗为 (18) 当E[(m,n),d]>Ecd[(m,n),di]时,数据的压缩和解压对整个链路才有效,即 (19) 计算di,得 (20) (21) 根据上述分析可知,当数据进行首次压缩和解压时,网络总能耗为 (22) (23) 计算上式,可得 (24) 上述讨论给出了数据在后继传输路径中,进行压缩与解压以及不被后继节点进行压缩与解压时,任意两节点之间距离满足的必要条件。从讨论2和讨论3中可以看出,ASD-MC算法不仅确保数据传输时所需能量最少,同时也实现了传输距离的最优设计。在数据传输时,ASD-MC算法均衡了全网能量,以汇聚增益值较大的节点完成了数据转发过程,减少了数据传输的跳数,实现了动态实时处理,减少了网络时延,抑制了节点能量消耗,延长了网络生存周期。 在满足全网能耗最少的前提下,如果全网中所有传感器节点的融合度均达到100%,即完全融合,则cmax=1;数据在通信链路中进行传输时,数据包的大小始终不会发生改变,数据传输链路则是以Sink为根节点的最小生成树(Minimum Spanning Tree,MST)。反之,如果全网中所有传感器节点的融合度均为零,即零融合,则cmin=0。数据在通信链路中进行传输时,Sink节点融合后的数据包的大小等于各个节点数据包总量之和,数据传输链路则是以Sink为根节点的最短路径树(Shortest Path Tree,SPT)。一般来说,在无线传感器网络数据传输过程中,上述两种极端情况很难出现,数据融合度c介于[0,1],其ASD-MC算法描述如下: 步骤1 给定无线传感器网络G=(V,E),任意边集E中存在通信链路e=(m,n);利用式(17)计算在通信链路e上传输k比特数据时所消耗的网络能量E[(m,n),di]。 步骤2 根据式(10)和式(11)计算数据融合度。 ① 当数据融合度满足式(10),且保证全网节点均达到100%,即cmax=1时,此时全网构成的是以Sink节点为根的最小生成树MST。 ② 当数据融合度满足式(11),即cmin=0时,此时全网构成的是以Sink节点为根的最短路径树SPT。 步骤3 当数据融合度介于[cmin,cmax]时,根据式(14)和节点距离相关系数τ计算此时的数据融合度。 步骤4 利用式(17)和式(18)判断链路中的数据是否要完成压缩与解压过程。 ① 当E[(m,n),d]>Ecd[(m,n),di]时,要对链路中的数据进行压缩与解压操作。 ② 当E[(m,n),d]≤Ecd[(m,n),di]时,除源节点与Sink节点外,数据不在任意节点进行压缩与解压操作。 步骤5 在满足式(20),数据在传输给下一跳节点时,将当前节点与下一跳节点的di以及该节点与下一跳节点的位置存储在该链表中;当数据遍历完该路径上所有节点时,该链表中的节点集合构成了最小生成路径。 步骤6 在满足式(21)时,数据压缩与解压过程在源节点与Sink上完成,在其他节点上均不再进行压缩与解压操作。数据在源节点上完成压缩操作后,将数据包沿dv方向传输至下一跳节点;此时,链表记录dv以及该节点与下一跳节点的位置信息;当数据遍历完该路径上所有节点时,在Sink节点上进行解压操作后,该链表中的节点集合构成了最短生成路径。 基于上述分析,ASD-MC算法所生成的聚合树性能介于MST和SPT之间,因此ASD-MC算法适应用于具有不同数据融合度的无线传感器网络。ASD-MC算法既兼顾了MST和SPT的特性,又具有自适应数据汇聚能力。在ASD-MC算法中,数据传输的下一跳节点将根据数据增益原则,判断是否对该数据进行汇聚。如果满足汇聚条件,则对该数据进行汇聚,以减少节点数据的传输量,抑制节点能量的消耗;反之,则对该数据选择最短路径进行传输,以获取最佳传输方式。 为了进一步验证ASD-MC算法的性能,实验采用Matlab2019b作为仿真平台,参数设定如表1所示。当节点的通信半径Rc增大时,节点距离相关系数τ也会随之增大,即τ→1,数据融合方式趋于完全融合;当节点的通信半径Rc减少时,节点距离相关系数τ也会随之减少,即τ→0,数据融合方式趋于零融合。因此,τ的取值范围定义为τ∈[0.2,8]。为了保证数据的可靠性,在数据传输过程中,笔者采用无损压缩方式对数据进行压缩与解压处理,利用第2代小波分解的零树编码算法(Embedded Zerotree Coding based on Second Generation Wavelets,EZC_SGW)[18]对传输数据进行无损压缩处理,因此数据压缩比定义为γ∈[6,10]。在仿真实验中,将ASD-MC算法与QCHBRP[12]和CS-MDGA[13]以及CS-CARDG[14]在网络能量开销和平均时延方面进行对比,能量模型采用Heinzelman自由空间和多路衰减模型[19]。 表1 仿真参数说明 图3给出了4种算法在不同参数以及不同监测区域作用下的网络剩余能量对比示意图。 随着时间的推移,图3(a)至图3(d)的网络剩余能量均有所下降;而图3(e)至图3(f)的则趋于平稳。现以图3(c)和图3(f)为例进行说明。图3(c)是以200 m×200 m作为监测区域,τ=0.4,γ=7。当网络运行时间在650 s时,ASD-MC算法网络剩余能量约为1 245 J,QCHBRP算法网络剩余能量约为1 068 J,CS-MDGA算法网络剩余能量约为848 J,CS-CARDG算法网络剩余能量约为635 J;当网络运行至800 s时,ASD-MC算法网络剩余能量约为1 155 J,QCHBRP算法网络剩余能量约为960 J,CS-MDGA算法网络剩余能量约为740 J,CS-CARDG算法网络剩余能量约为500 J。从上述分析可以得到,随着网络运行时间的增加,4种算法的网络剩余能量均有所下降,但ASD-MC算法下降幅度小于其他算法。图3(f)给出了在400 m×400 m监测区域下,τ=0.6,γ=8时,4种算法网络剩余能量对比示意图。从图3(f)可以看出,随着网络运行时间的增加,4种算法的网络剩余能量均趋于平衡,变化的幅度较小。 (a) 200 m×200 m,τ=0.2,γ=6 (d) 400 m×400 m,τ=0.4,γ=7 综合上述分析,当网络剩余能量随着不同情况发生变化时,其主要原因在于ASD-MC算法优先考虑了传输数据是否在某节点处发生汇聚。第1种情况,数据未汇聚,即数据在零融合网络中进行传输时,ASD-MC算法不考虑汇聚开销,则按照最短路径原则将数据信息从源节点发送至Sink节点;第2种情况,数据完全汇聚,即数据在非零融合网络中进行传输时,ASD-MC算法在考虑汇聚开销的同时,利用无损压缩对传输数据的长度进行动态调节,以减少传输数据量,抑制了节点能量的快速消耗,延长了网络生存周期。其他算法并没有考虑汇聚与压缩等因素,只是依靠节点自身能量完成数据信息的传输。因此,在网络剩余能量对比中,那3种算法的网络剩余能量均小于ASD-MC算法,其平均数值减少约10.29%。 图4给出了4种算法在不同监测区域下的网络时延对比示意图。 随着传感器节点数量的增加,4种算法的网络时延也随之增加,但ASD-MC算法增加幅度最小。现以图4(a)和图4(d)为例进行分析。图4(a)是以200 m×200 m作为监测区域,当传感器节点数量为120时,ASD-MC算法的网络时延约为0.09 s,QCHBRP算法的网络时延约为0.13 s,CS-MDGA算法的网络时延约为0.16 s,CS-CARDG算法的网络延时为0.22 s多;当传感器节点数量为180时,ASD-MC算法的网络时延约为0.11 s,QCHBRP算法的网络延时约为0.15 s,CS-MDGA算法的网络延时约为0.17 s,CS-CARDG算法的网络延时少于0.23 s。图4(d)是以400 m×400 m作为监测区域,当传感器节点数量为1 600时,ASD-MC算法的网络时延约为0.235 s,QCHBRP算法的网络延时约为0.263 s,CS-MDGA算法的网络延时约为0.270 s,CS-CARDG算法的网络延时约为0.293 s;当传感器节点数量为1 900时,ASD-MC算法的网络时延约为0.235 s,QCHBRP算法的网络延时约为0.263 s,CS-MDGA算法的网络延时约为0.273 s,CS-CARDG算法的网络延时约为0.295 s。 综合上述分析,ASD-MC算法网络时延优于其他算法的原因在于:随着传感器节点数量的增加,将会导致汇聚增益和全网能量开销E(n,S)随之增加。ASD-MC算法根据每一跳节点的汇聚增益数值自适应地确定是否进行汇聚。当汇聚开销过大时,ASD-MC算法可以通过动态调整参数大小来改变路由策略,以减少数据汇聚次数,抑制节点能量的开销,达到全网节点能量均衡化的目的。在网络时延对比中,ASD-MC算法网络时延均小于其他算法的网络时延,其平均数值减少约12.57%。 (a) 200 m×200 m,τ=0.2,γ=6 (b) 400 m×40 m,τ=0.2,γ=6 针对信道内数据冲突与碰撞等不稳定因素,提出了一种面向最小能耗自适应汇聚路由判定算法。ASD-MC算法首先分析了汇聚增益和数据融合度之间的函数关系,给出了距离相关参数与通信半径之间的比例关系;而后讨论了数据融合度介于最小值与最大值之间的函数关系,证明了在下一跳节点非融合时的后继节点中,也不会再进行数据融合处理。利用能量关系,讨论了压缩与解压、连续性传输的非压缩与非解压时的任意两节点距离的函数关系,分析了ASD-MC算法的实现过程与方法;最后,通过仿真实验与其他算法在网络剩余能量和网络时延上进行比对实验,验证了ASD-MC算法的有效性和实效性。 未来工作主要集中在借助于压缩感知理论实现备份路由的优化以及如何提高不可靠链路对数据重构精度等方面。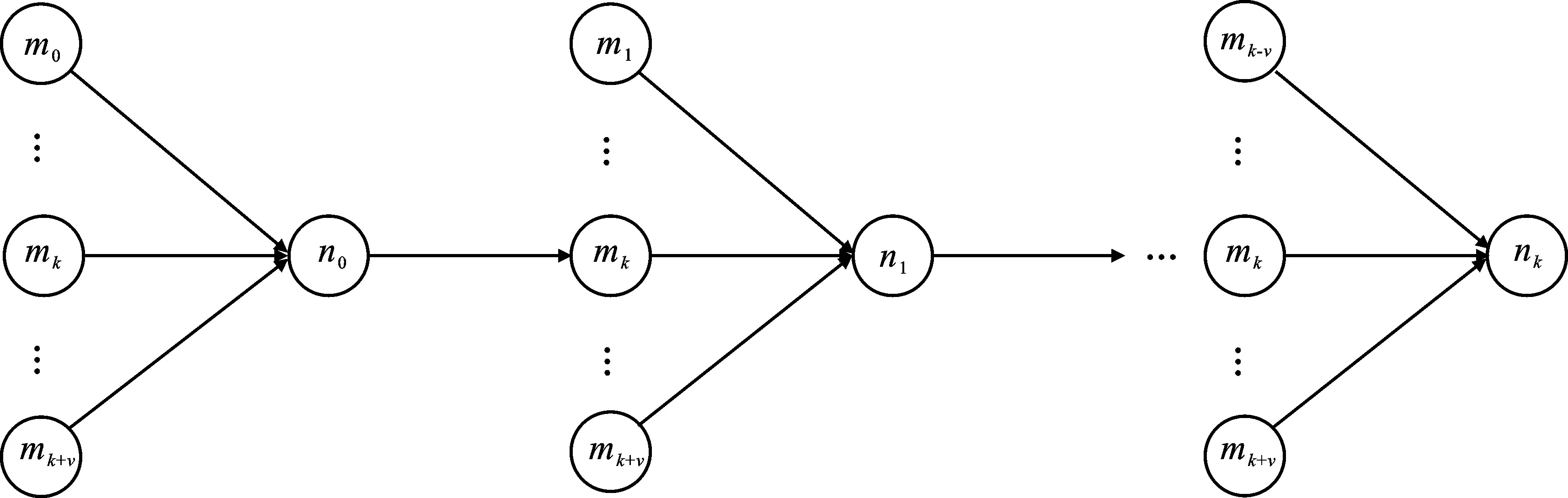
2.2 欧氏距离分析
2.3 ASD-MC算法分析
3 性能评价
3.1 网络剩余能量
3.2 网络时延
4 总 结

