一种ADC不同步下的数字干涉仪校正方法*

孙洪波，韩学涛，王传根，王 超

(电子信息控制重点实验室,成都 610036)

0 引 言

干涉仪测向是一种高精度的测向体制,广泛应用在单站无源测向定位系统中，是电子侦察的一项重要技术。随着工艺水平的提高，系统的集成度越来越高，适中的规模、高精度的性能使得干涉仪应用越来越广泛。

通过通道间相位差的测量计算目标来波的到达方向，通道间的相位一致性直接影响测量精度，但侦察应用的宽频带特性使得通道间的相位和幅度一致性很难保证，因此通道的幅相校正是系统校正的一个重要环节。

传统的通道校正方法主要针对天线、高增益放大、变频通道、滤波等环节引起的不一致性进行校正，目前还没有明确的在干涉仪应用中针对模数转换器(Analog-to-Digital Converter，ADC)采集不同步的校正方法报道。关于ADC采集更多的是介绍如何进行同步设计，这对外部高速时钟电路与参考电路设计提出了较高的要求，特别是模块间的高速同步参考，国内目前还缺少自主可控的高速时钟参考数字芯片，尤其针对高可靠应用场景，系统设计将变得异常复杂。

本文介绍的校正系统旨在解决多路ADC采集同步不稳定引起的通道相位关系变化，采用简单的校正系统设计方法进行不一致性修正，可以简化系统中多路ADC同步设计，最终实现较高的目标方向测量。

1 测向原理

图1为目前数字干涉仪测向处理的模型，可以看出，某一远距离对象辐射的电磁信号通过空间传输，进入接收设备的天线，通过射频通道的低噪放大、变频等处理，射频信号转换成ADC可采集的中频信号，在中频上完成ADC采集与后续数字处理，最终在数字上完成通道间相位差测量。

图1 干涉仪原理模型

由图1可知，辐射电磁波信号到达接收设备的不同天线时，会存在一个路程差Δd，该路程差使得同一个信号到达两个天线的初相不同，最终体现为两个通道的测量相位差。测量得到输入相差Δφ，折算信号入射角度。干涉仪测向的数学公式为

(1)

式中：Δφ入为由波程差造成的输入来波相位差，即测量的真实相位差；c为光速；f为信号频率；L为两个天线之间的间距。

2 不同步影响分析

真实系统中，直接测量出的相位差是经过射频通道、数字处理等环节“污染”后的相位差。为了能真实的测量出来波输入相位差，需要扣除接收设备附加的相位差，这个过程称为校正。

测量值、真实的相位差、附加的误差这三者之间的关系可表述为

Δφ测量=Δφ输入+Δφ附加。

(2)

式中：Δφ输入为来波信号到达两个天线口面的相位差真值，Δφ附加为接收设备模拟通道和数字处理环节共同引入的误差，Δφ测量为接收设备最终输出的相位差测量结果。

当入射角度θ为0时，Δφ输入为0，此时Δφ测量=Δφ附加。

当Δφ附加是一个时不变值或缓变量时，可在内场静态校正中测量出Δφ附加，以此作为Δφ校正校正值，从而完成真实测量时来波方向θ的测量。

随着ADC采样率的提高，ADC器件与处理器间采用多路并行传输，输出数据速率为采样时钟的分频。对于很多类型的ADC芯片而言，输出分频相位不可控，在不同次上电中完全随机，导致通道间的时延相差较大，相位差差异大。

如图2所示，采用1分4的降速方案，面临4种不同相位的可能。

图2 时钟四分频相位关系图

以1 000 MHz采样来看，输出时钟为250 MHz，180°相位翻转导致时延上差异2 ns，造成在500 MHz带宽范围内的相位波动可达100°以上。

针对这个不同步相位影响，常规的校正方法是测量出不同步引起的时延差异Δt，在已知信号频率下计算这个相位差异补偿测量相位差。校正系统框图如图3所示。

图3 校正系统框图

在校正模式下，校正源工作，模拟开关切换到校正源输入。假设功分器、模拟开关通道相位差可忽略，则可测量得到校正信号相位差，因此有

(3)

测量出Δt，便可计算出不同步引起的相位污染：

ΔφADC不同步附加=2×π×f输入×Δt=

(4)

实际上系统测量得到的相位差是模糊相位值：

Δφ校正测量=mod(2π×f校正×Δt,2π)。

(5)

为了避免模糊，要求f校正小于ADC采集时钟的1/4，校正源要选择一个低频的时钟源，但从式(4)可以看出ADC不同步引起的测量误差是Δφ校正测量误差的f输入/f校正倍，因此不能直接采用测量Δt的方法进行系统校正。

上述分析中还忽略了校正源功分器与模拟开关的相位差。为了能够取得高精度的相位测量，需要将功分器与模拟开关的相位考虑在内。

3 系统校正方法设计

本文基于上述常规校正方法，设计了如下的三步校正流程，消除功分器、模拟开关、测量误差等环节影响。

第一步，内场校正记录。

在内场暗室标校时，将目标信号入射角设置为0°，将模拟通道开关前后切换到校正信号与通道信号，开展校正信号测试和目标信号测试，最终得到两组相位差，分别是校正信号的两个通道相位差Δφ测量1、目标信号的两个通道相位差Δφ测量2。

在目标信号入射角为0°时，Δφ输入为0°，依据信号的传输途径，Δφ测量1、Δφ测量2有如下关系：

校正工作时相位差为

Δφ测量1=Δφ输入+Δφ模拟+Δφ数字=

Δφ功分+开关+f校正×Δt1;

(6)

0°目标工作时相位差为

Δφ测量2=Δφ输入+Δφ模拟+Δφ数字=

Δφ通道+开关+f射频×Δt1。

(7)

式(6)和(7)中：Δt1为此次上电工作中两个通道ADC不同步引起的时延差。

第二步，实际目标侦收。

在实际侦收过程中，系统加电后两个通道ADC不同步引起的时延差变为Δt2。首先切换到校正信号工作，测量得到通道间相位差Δφ测量3，校正测量完成后切换到目标侦收状态，目标处于X角度，测量得到通道间相位差Δφ测量4。两组相位差分别有如下关系：

Δφ测量3=Δφ输入+Δφ模拟+Δφ数字=

Δφ功分+开关+f校正×Δt2，

(8)

Δφ测量4=Δφ输入+Δφ模拟+Δφ数字=

Δφ输入+Δφ通道+开关+f输入×Δt2。

(9)

通过式(6)和式(8)可消除校正用功分器与模拟开关相位差Δφ通道+开关的影响:

Δφ测量1-Δφ测量3=f校正×(Δt1-Δt2)。

(10)

通过式(7)和式(9)可消除校正用功分器与模拟开关相位差Δφ功分+开关的影响：

Δφ测量2-Δφ测量4=f输入×(Δt1-Δt2)-Δφ输入。

(11)

通过式(10)和式(11)可以推出

(12)

式中：Δφ测量1与Δφ测量2为地面内场校正测试流程中对校正源信号与目标信号测量相位差的记录值，仅需在地面内场校正测试一次，可供后续使用；而Δφ测量3为真实目标侦察阶段每次加电时通道间校正源信号的测量相位差，Δφ测量4则为同一次加电期间对空间中真实目标信号的测量相位差。

第三步，寻真值。

经过第二步中式(12)的处理，最终结果测量误差是(Δφ测1-Δφ测3)测量误差的f输入/f校正倍，系统相位测量误差被放大了。

实际上式(12)中，

(Δφ测1-Δφ测3)=2π×f校正×(Δt1-Δt2),

(13)

Δt1-Δt2为两次测量时两个通道ADC输出时钟延迟差Δt的变化，Δt无法测量出真实值，但从图2的ADC输出相位不同步可以看出，Δt的变化一定为采样时钟周期的整数倍。以图2的四分频为例，Δt1-Δt2仅有7种可能取值：

Δt1-Δt2∈[-3Ts,-2Ts,-Ts,0,Ts,2Ts,3Ts]。

因此，可以利用测量出的(Δφ测1-Δφ测3)推算出真实的(Δt1-Δt2)真:

(Δt1-Δt2)真=Round((Δφ测1-Δφ测3)/(2πf校正Ts))。

(14)

依据式(14)有

(Δφ测1-Δφ测3)真=2πf校正(Round((Δφ测1-Δφ测3)/(2πf校正Ts)))Ts。

(15)

将式(15)代入式(12)，可演变为

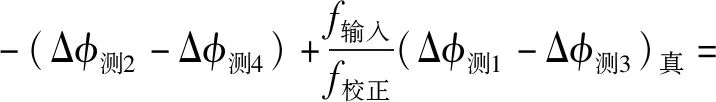
-(Δφ测2-Δφ测4)+2πf输入×

(Round((Δφ测1-Δφ测3)/(2πf校正Ts)))Ts。

(16)

从式(16)可以看出，最终的测量误差与(Δφ测2-Δφ测4)测量误差相当。

经过上述三步的处理，最终消除了功分器、模拟开关、ADC不同步、校正信号测量误差等因素对高精度相位差的测量影响，实现了高精度测向。

实际系统中两个模拟通道间的相位关系随频率是有差异，信号频率本身未知，Δφ测量2随频率是变化的，因此需要测量出所有可能工作频点下的Δφ测量2。在第三步式(16)计算时依据测量得到的信号频率查取对应频点的Δφ测量2，消除天线、射频、功分器等环节随频率差异的影响。工程上为了减小Δφ测量2的存储容量以及系统测试难度，可采用一定频率间隔进行抽样，频率间隔的大小依据频率变化引起的相位差差异大小确定。

4 实验验证

在某实验系统中，ADC采样率高达10 GHz，采样后数据降速使用，采用16分频，数据时钟为625 MHz，ADC采集器本身无法实现多器件间的ADC同步，因此存在16种分频相位可能，每次上电后通道间相位关系不固定。

采用本文设计的校正方案，选用100 MHz校正源时钟，首先在内场暗室进行了系统校正测试，接收设备装载于天线转台上，目标发射天线固定于发射支架上，调整转台角度，使得目标发射信号相对于接收设备处于入射角为0°的位置，记录Δφ测1、Δφ测2，将此数据作为后续测试的原始依据。

转动天线转台，使得目标信号相对于接收设备来说处于多个不同的入射角，同时给接收设备多次加断电，验证方案的可行性。

该系统中两个通道在两次加电过程中的变化有31种，即Δt1-Δt2∈[-15Ts:Ts:15Ts]。

测量的(Δφ测1-Δφ测3)与推算出的(Δφ测1-Δφ测3)真差如图4所示。

图4 校正信号相位测向误差

从图4可以看出，在高信噪比情况下，(Δφ测1-Δφ测3)测量精度很高，误差可控在0.5°以内，但经过f输入/f校正放大后输入相位误差可达±50°左右，如果不经过高精度修正，将严重影响系统测向精度。

通过式(15)的真值搜索处理后，多次上电两个通道Δφ输入测量情况如图5所示,可以看出即使在灵敏度状态下相位测量精度可控制在10°以内，满足系统测向精度要求。

图5 13 dB接收灵敏度下目标相位测量误差

如图6所示，目标信号相对于收设备的入射角分别为-40°、-30°、-20°、-10°、-10°、0°、10°、20°、30°时，对接收设备多次开关电，入射角的测量误差均能在1°以内，满足系统测向精度要求。

5 结 论

本文从干涉仪的基本原理出发,分析了多通道ADC采集不同步情况下相位差测量影响，设计了三步骤的通道相位差校正方法，并进行了理论推导和实验验证，取得了较好的实验效果。该方法具有测量精度高、系统设计简单、可靠性高等优点，具有通用性与广阔的应用前景。