基于VMD的调频连续波雷达生命信号提取*

屈乐乐，刘淑杰，杨天虹，张丽丽，孙延鹏

(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

0 引 言

非接触式生命探测雷达通过发射电磁波至人体并接收人体反射回波，再通过相应的信号处理来提取人体的生命体征信号[1]，主要采用的雷达体制包括超宽带脉冲雷达、单频连续波雷达和调频连续波(Frequency Modulated Continuous Wave，FMCW)雷达。文献[2]中采用超宽带脉冲雷达清晰地检测到呼吸和心跳运动，呼吸的正确检测率超过95%，但是超宽带脉冲雷达无法传输高能量信号，这使得信噪比和精度降低，并且由于其宽带特性，不利于系统集成和低功耗运行[3]。文献[4]提出了一种基于双圆极化贴片天线的单频连续波雷达系统，可以准确地检测到志愿者的呼吸和心跳运动，然而单频连续波雷达不具有距离分辨率，故不能很好地区分杂波和多目标[5]。相比于超宽带脉冲雷达和单频连续波雷达，FMCW雷达带宽大，具有更高的距离分辨率和速度分辨率，且具有区分多个目标和提取目标微动信号的能力，同时系统集成度高，功耗低，硬件实现相对简单，受噪声影响较小。因此，本文选择FMCW雷达进行生命信号监测。

近年来，基于FMCW雷达的生命信号提取技术得到了国内外研究者的广泛关注。文献[6]利用快速傅里叶变换(Fast Fourier Transform，FFT)对相位信号进行处理，从差拍信号中提取呼吸和心跳信号。但是FFT不具有自适应性，无法分离低频杂波、呼吸信号、呼吸谐波信号和心跳信号，使得所提取的呼吸和心跳信号存在误差。文献[7]采用聚类经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)分离呼吸和心跳信号，该算法是一种改进的经验模态分解，能够有效减少经验模态分解存在的模态混叠问题。但是EEMD在分解过程中加入高斯白噪声，分解完成后若高斯白噪声没有被完全抵消，则在本征模态函数(Intrinsic Mode Function，IMF)中可能会存在对生命信号提取结果造成较大影响的噪声信号。

针对上述问题，本文提出了一种基于变分模态分解(Variational Mode Decomposition，VMD)的FMCW雷达生命信号提取算法。VMD算法是由Zosso团队[8]于2014年提出的一种信号分解估计方法，具有自适应、非递归的特点，该算法通过构造并求解变分问题实现对原始信号的分解，能有效避免模态混叠、过包络、欠包络、边界效应等问题，具有较好的复杂数据分解精度及较好的抗噪声干扰等优点[9]。实测结果表明，基于VMD的生命信号提取方法相比于EEMD，能够准确有效地分离生命体征信号。

1 FMCW雷达生命信号模型

FMCW雷达信号调制方式通常分为锯齿波和三角波两种，本文选用锯齿波，即发射信号频率随时间按如图1所示的锯齿波变化。图中fc为发射信号中心频率，B为发射信号带宽，T为发射信号周期，td表示发射信号与接收信号之间的时间延迟。

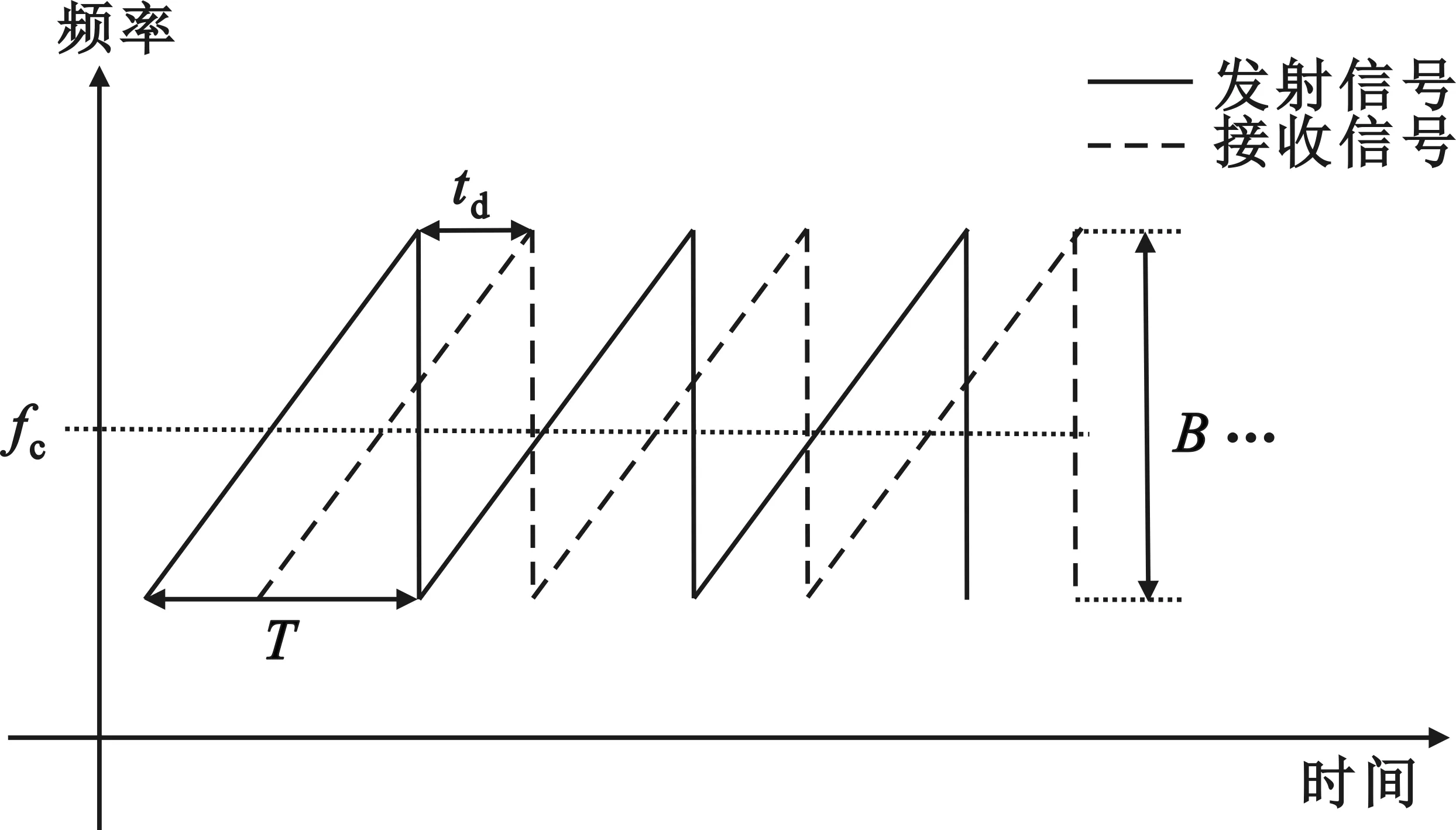
图1 FMCW雷达锯齿波波形频率

假设一个发射周期时间内发射信号为复chirp信号，以重复周期T连续发射N个FMCW信号。发射时刻τ=nT(n=0,1,2,…,N)，称为慢时间;以发射时刻为起点的时间用t表示，称为快时间。则发射信号可以表示为

sT(t)=exp(j(2πfct+πγt2+φ))。

(1)

式中：γ=B/T为锯齿波斜率，φ为初始相位，t∈[-T/2，T/2]为快时间。

假设人体呼吸和心跳引起的胸腔微动等效为简谐振动，则人体到雷达的瞬时距离x(τ)可表示为

x(τ)=d0+xr(τ)+xh(τ)=

d0+Arsin(2πfrτ)+Ahsin(2πfhτ)。

(2)

式中：τ为慢时间，d0表示雷达天线到人体胸腔表面的起始距离，Ar和Ah分别为呼吸和心跳信号的幅度，fr和fh分别为呼吸和心跳信号的频率。则在接收端回波信号可表达如下：

sR(t)=σsT(t-td)。

(3)

式中：σ为接收信号的幅度，该参数主要受雷达散射截面以及传播损耗的影响；td=2x(τ)/c，c为电磁波在真空中的传播速度。

解线性调频是用发射信号与回波作差频处理。在一个t∈[-T/2，T/2]内，经解线性调频得到的差拍信号sb(t)如公式(4)所示：

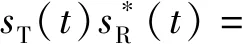
σexp(j(ωbt+φ(τ)))。

(4)

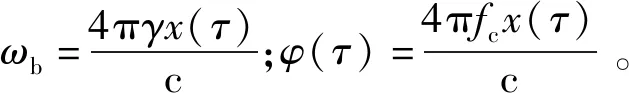
2 信号处理

基于FMCW雷达的生命信号提取包括目标距离像重构、相位提取、相位信号VMD分解、呼吸心跳频率估计四个步骤，流程图如图2所示。

图2 呼吸和心跳信号提取流程图

2.1 目标距离像重构和相位提取

将模数转换后的差拍信号按列堆叠为M×N维矩阵M[mn]，该矩阵由公式(4)中的快时间t和慢时间τ分别离散化得到，其中m=0,1,…,M-1；n=0,1,…,N-1，M和N分别为快时间维采样个数和慢时间维采样个数。目标距离像重构和相位提取的详细流程如下：

Step1 对差拍信号矩阵M[mn]的每一列执行距离维FFT得到距离剖面矩阵R[mn]。

Step2 通过计算每个距离门内信号的方差，将方差最大的距离门m*作为人体目标所在的距离门，得到目标所在距离门对应的信号s[n]=R[m*n]。

Step3 提取信号s[n]的相位φ[n]，对φ[n]进行解缠绕，过程如下：当φ[n+1]-φ[n]>π时，φ[n+1]减去2π，当φ[n+1]-φ[n]<-π时，φ[n+1]加上2π。将解缠绕得到的相位信号记为φ[n]。

Step4 健康成年人的呼吸和心跳的频率范围为0～2 Hz[10]，根据该频率范围，对相位信号φ[n]使用截止频率为2 Hz的低通滤波器滤掉高频噪声。

2.2 基于VMD的相位信号分解

由于信号极值点对EEMD分解结果影响较大，若分布不均匀会出现模态混叠。因此，本文采用VMD对低通滤波后的相位信号进行模态分解。VMD能够将多分量信号一次性分解成多个单分量信号，避免了迭代过程中遇到的端点效应和虚假分量问题。算法整体框架是变分问题，假设每个模态是具有不同中心频率的有限带宽，使得每个模态的估计频谱带宽之和最小，约束条件是各个模态之和等于原始信号φ[n]。为解决这一变分问题，使用交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)不断更新各模态及其中心频率，逐步将各模态解调到相应的基频带，最终各个模态及相应的中心频率被一同提取出来。VMD分解的具体步骤如下：

Step1 假设相位信号φ[n]被分解为K个模态分量uk(n)(1≤k≤K)，模态分量为具有中心频率ωk(1≤k≤K)的有限带宽信号，同时各模态的估计带宽之和最小，约束条件为所有模态之和与原始信号相等，则相应约束变分表达式为

(5)

Step2 求解式(5)，引入惩罚因子α和拉格朗日乘子λ(n)，将约束变分问题转变为非约束变分问题，得到增广拉格朗日表达式为

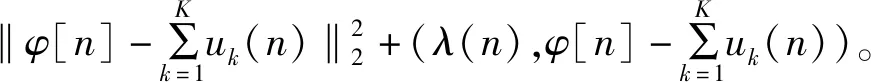
(6)

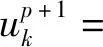
(7)

(8)

式中：sgn代表符号函数。

Step5 将公式(8)第一项中的ω+ωk用ω进行替换，再利用实信号的Hermitian对称性可将式(8)转换成非负频率区间的积分形式：

(9)

通过消除第一项变量，此时二次优化问题的解为

(10)

(11)

VMD算法的具体步骤如下：

Step3 更新拉格朗日因子λ:

2.3 呼吸心跳频率估计

在实际测量中，呼吸信号的幅度约为心跳信号幅度的10倍[10]，而接近心跳频率的呼吸谐波很可能有相近的幅度，因此如何确定呼吸和心跳信号的主要成分在哪个IMF中就显得尤为重要。为解决该问题，本文根据模态判别准则对每个IMF中呼吸和心跳信号能量占比进行计算，利用符合条件的IMF实现生命信号重构。根据健康成年人的呼吸频带为0.2～0.5 Hz，心跳频带为0.8～2.0 Hz[10]，在频域上对每个IMF计算呼吸和心跳的能量百分比，表达式如下：

(12)

式中：E(k)为第k个IMF的频域能量，Er(k)和Eh(k)分别表示第k个IMF中呼吸和心跳频带内的能量，δr和δh分别表示判断呼吸和心跳的能量比阈值。根据文献[11]的结果，当δr和δh取值为0.5时，呼吸和心跳信号的提取效果达到最佳。因此，本文将δr和δh均取值为0.5。将满足模态判别准则的IMF分量相加即可得到重构的呼吸和心跳信号。重构呼吸信号sr(n)和心跳信号sh(n)表达式如下：

(13)

(14)

对重构信号进行FFT，即可得到生命信号的估计频率。

3 实验结果

实验中采用Ancortek公司所生产的SDR-KIT 2400AD2雷达套件进行实验，该雷达为双通道的厘米波雷达，本文仅用一个接收通道；天线采用喇叭天线，天线增益为15 dBi。FMCW雷达参数如表1所示。实验采用接触式传感器HKH-11C(呼吸波传感器)和HKG-07C(红外脉搏传感器)得到呼吸和心跳频率的参考值，采样频率分别为200 Hz和50 Hz。

表1 FMCW雷达参数

实验中选取的EEMD参数如下：信号中添加加性高斯白噪声的方差为0.2，算法执行经验模态分解次数为50。VMD的参数如下：初始化估计带宽α=106，直流参数DC=0,收敛条件参数tol=10-6。原始相位信号中包含呼吸信号、呼吸谐波信号、心跳信号和低频噪声信号，为获得较好的分解效果，取模态分解个数K=6。

实验场景如图3所示，一名健康的男性志愿者坐在0.4 m高的凳子上，佩戴接触式传感器，面向距离人体1.5 m远的雷达天线，保持正常呼吸。

图3 实验场景

对实测数据差拍信号矩阵做256点距离维FFT后得到距离剖面矩阵如图4所示。经最大方差法计算可知，目标位于第20个距离门处。

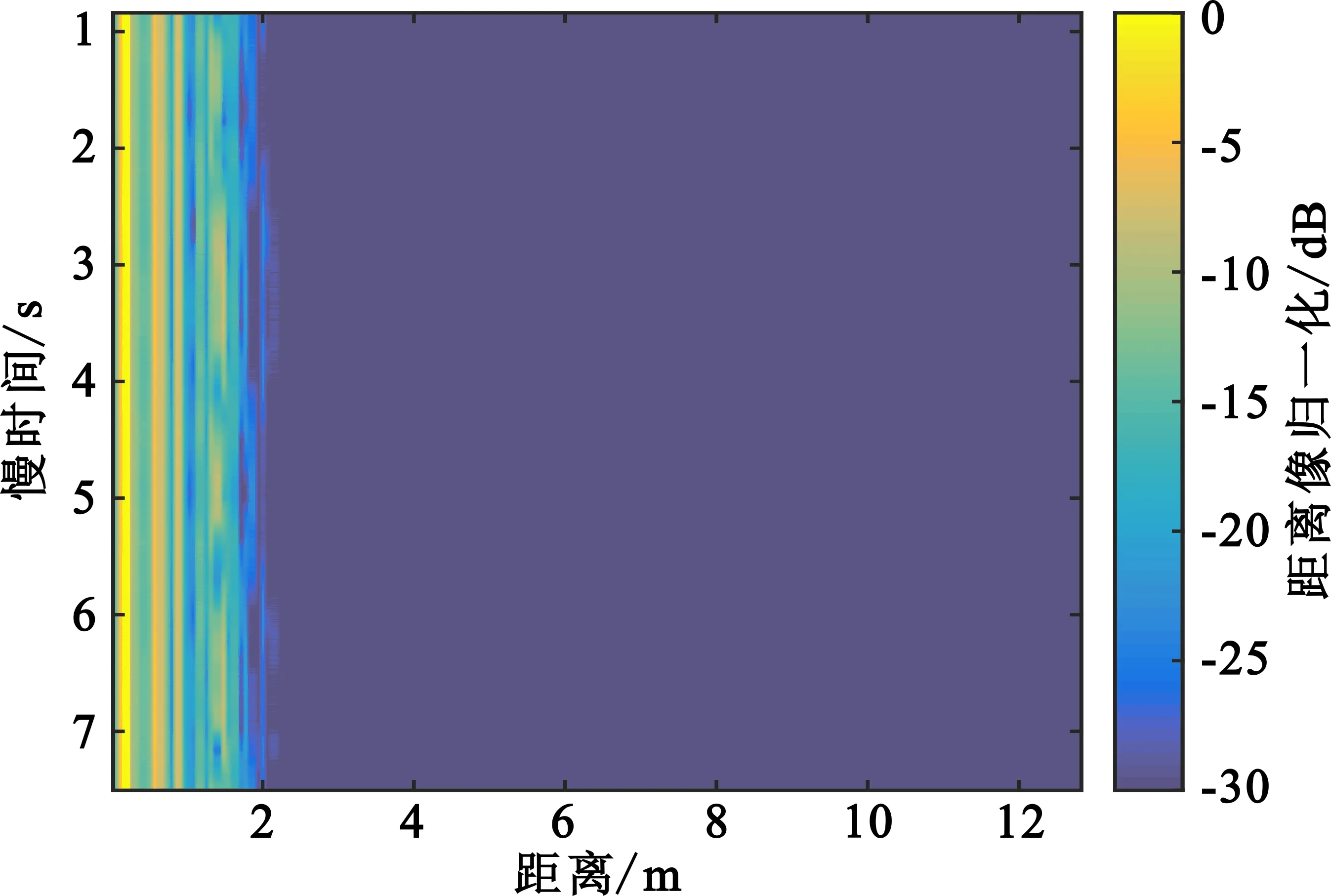
图4 距离剖面图

利用最大方差法得目标所在距离门后，提取相位信号并使用低通滤波器对相位信号进行滤波，对滤波后的相位信号进行EEMD分解，分解结果如图5所示。从图中可以看出，相位信号被自适应地分解为9个IMF，每个IMF按频率由高到低排列。对每个IMF分量中的呼吸和心跳能量占比进行计算发现，IMF8和IMF9的呼吸能量占比超过阈值，IMF6和IMF7的心跳能量占比超过阈值，因此用IMF8和IMF9、IMF6和IMF7分别对呼吸、心跳信号进行重构。重构所得生命体征信号的波形和频率如图6所示。由图6(c)可知重构呼吸信号频率为0.387 5 Hz,重构信号中存在杂散频率分量；由图6(d)可知重构心跳信号频率为1.35 Hz，且重构信号频率中存在明显的其他频率，因此可判断EEMD分解存在模态混叠且无法有效抑制杂散频率分量。

图5 EEMD分解结果

图6 EEMD生命重构信号

对滤波后的相位信号进行VMD分解，可得到6个IMF，分解结果如图7所示。同理可得，呼吸能量主要集中在IMF1，心跳能量主要集中在IMF4。重构所得生命体征信号波形和频率如图8所示。

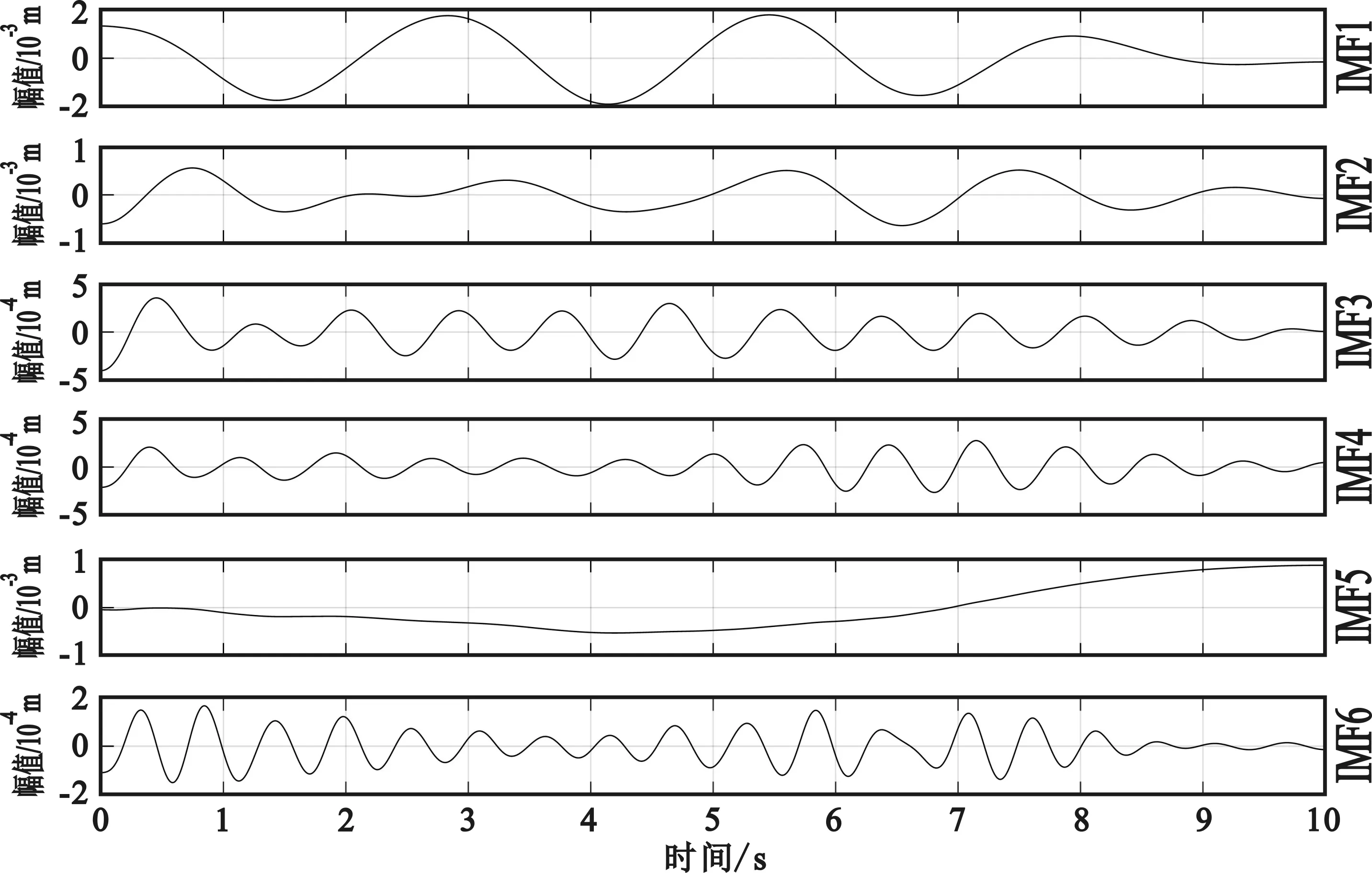
图7 VMD分解结果

图8 VMD生命重构信号

由图8(c)、(d)可知重构呼吸、心跳信号的频率分别为0.375 Hz、1.338 Hz，心跳信号频谱图中存在的1.488 Hz信号为呼吸信号的4次谐波。对重构信号幅频图进行比较可发现，相较于EEMD，经VMD分解后重构的心跳信号有效抑制了呼吸谐波和杂散频率分量对心跳信号的影响。

为分析本文算法的性能，对重构后的呼吸心跳信号从时域上估计呼吸和心跳频率。相对误差(Relative Error,RE)定义如下：

(15)

式中：f1为通过接触式传感器得到的生命信号频率，f2为通过雷达非接触式测量得到的生命信号频率。EEMD和VMD所得呼吸心跳信号频率、接触式传感器所得呼吸心跳信号频率及RE如表2所示。

表2 生命信号频率提取性能比较

由表2可知，VMD所得呼吸和心跳信号频率RE值分别为2.50%、2.45%，EEMD所得呼吸和心跳信号频率RE值分别为0.75%、3.37%。由RE对比结果可知，EEMD分解提取呼吸信号的频率误差要小于VMD分解，但经VMD分解得到的心跳信号效果优于EEMD。

为进一步衡量VMD和EEMD提取生命信号的准确性，采用重构结果信噪比(Signal-to-Noise Ratio，SNR)进行量化对比。重构结果SNR定义如下：

(16)

式中：A表示生命信号的幅度,sqr为平方函数，sum为求和函数，sqrt为开根号函数，Q为噪声样本数量。重构结果SNR描述了生命信号与噪声的比值，其中噪声不包含直流和生命信号。为验证VMD的有效性，列出两名志愿者的重构结果SNR，志愿者1如图3所示，志愿者2为健康成年女性。VMD和EEMD重构结果SNR如表3所示。

表3 重构结果SNR

VMD所得志愿者1和志愿者2的呼吸和心跳重构结果SNR分别为36.94 dB、35.91 dB和37.23 dB、34.24 dB，EEMD所得志愿者1和志愿者2的重构结果SNR分别为35.48 dB、29.93 dB和34.99 dB、28.62 dB。由以上数据可知，VMD分解后得到的心跳信号的重构结果SNR比EEMD分解后得到的心跳信号的重构结果SNR分别高5.98 dB、5.62 dB，VMD分解后得到的呼吸信号的重构结果SNR也分别高于EEMD分解1.46 dB、2.24 dB，这说明VMD的性能要优于EEMD。

由上述数据和分析可得出以下结论：与EEMD相比，VMD可更为准确的提取心跳信号，且有效抑制呼吸谐波和杂散频率分量对心跳信号的影响，同时，信噪比得到显著提高，表明了基于VMD的调频连续波雷达生命信号提取的可行性。

4 结 论

本文将VMD应用于提取FMCW雷达回波信号中的生命体征信号。首先对雷达差拍信号进行FFT、相位提取和低通滤波操作后利用VMD算法获得有限个IMF，然后通过模态判别准则对信号进行重构，最后对重构信号进行FFT得到呼吸和心跳信号频率。实测结果表明，VMD可较为准确地提取出生命体征信号且对杂散频率分量有较好的抑制作用，具有较为广阔的研究价值和应用前景。