预测控制对串级被控对象结构变化的要求：以串联CSTR为例

汪 磊 罗雄麟

（中国石油大学（北京）信息科学与工程学院自动化系）

化工过程的被控对象一般为多变量系统，通常以串级控制作为控制方法，但是随着先进化工工艺的发展，对过程控制的要求日渐提高。 当系统出现有约束、 强耦合以及强非线性等特性时，使用常规控制方法无法满足要求，因此出现了以模型预测控制（Model Predictive Control，MPC）为代表的先进过程控制（Advanced Process Control，APC），该方法在化工过程控制领域成为重要的研究方向［1～6］。

模型预测控制本质为一种基于数学模型并利用计算机实现的优化控制算法，在每一步控制周期内通过预测模型求解预测时域内的开环最优控制问题，获得当前控制周期内的最优控制动作，最终通过反馈校正实现闭环优化控制［7～9］。

在工业过程中应用预测控制时，通常由预测控制器接收串级控制最终输出的预测控制被控变量，利用稳态优化得到最优设定值，并且传输至串级主回路作为主回路PID控制器的给定值［10，11］。因此，预测控制的被控对象为包括串级控制回路在内的广义被控对象，这样可保证整个串级控制回路处在安全、稳定的控制范围内［12～14］。

但是另一方面，预测控制的引入也会增加部分附带的问题： 除了PID控制器的参数对预测控制的控制效果有一定影响，预测控制器的增加也相当于增加了串级回路数量，延长了预测控制系统的响应时间。 因此对于部分复杂控制场景可以通过简化串级回路， 即减少PID控制器与控制回路以获得更加高效的控制效果。

综合以上几个方面的考虑，笔者在预测控制的架构下，针对多入多出（Multiple Input Multiple Output，MIMO） 串级被控对象重新设计了预测控制系统，分析了常规控制层的串级控制结构进行必要简化的要求。 由于化工过程控制中的串级控制大部分为温度-流量串级控制方案， 笔者以串联连续搅拌反应釜 （Continuous Stirred Tank Reactor，CSTR）为例进行仿真对比，在传统预测控制系统基础上，给出了底层只有流量控制器与底层只有温度控制器两种控制方案。 将Matlab/Simulink软件作为仿真工具构建串联CSTR仿真平台，进行控制系统的设计与实现，结合实际情况探究此类问题的解决方法。 结果表明，在化工过程中应用先进控制时，宜简化常规控制层的串级控制结构。

1 串级被控对象在预测控制架构下多层串级存在的问题分析

在预测控制架构下，预测控制的输出送给常规控制作为给定值，相当于增加常规控制层中串级回路的数量，造成多层串级问题，最终导致常规控制层的组态复杂度增加，响应时间延长。 因此，针对此类复杂度高的问题，如何在传统预测控制结构的基础上通过简化结构降低系统复杂度，值得进一步探究。

在化工过程控制中， 通常由串级控制组成常规控制层， 并且在预测控制架构下作为预测控制被控对象， 串级回路的最终输出实时反馈回预测控制器［15，16］，控制结构框图如图1所 示。预测控制的引入相当于增加底层串级回路的数量，即双层串级回路变为多层串级回路，对于多入多出串级控制尤为明显。 并且由于多层串级的存在， 串级控制的主回路由常规情况下的定值控制转变为预测控制架构下的随动控制，由主回路转变为预测控制的副回路， 因此对应的主回路PID控制器参数是否需要整定也需要关注。

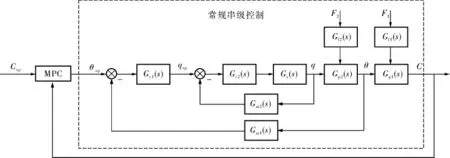
图1 预测控制架构下的常规串级控制结构框图

图1中，q、θ、C分别代表化工工艺装置内的流量、温度和浓度参数，qsp、θsp、Csp分别为对应的给定值；Gp1（s）、Gp2（s）分别为被控装置中主、副被控变量在稳态操作点由线性化得到的传递函数；Gm1（s）、Gm2（s）为反馈通道传递函数；Gc1（s）、Gc2（s）为主、副控制器传递函数；Gv（s）为流量控制回路中流量阀的传递函数；Gf1（s）、Gf2（s）为扰动通道传递函数，F1、F2分别为进入主、副被控对象的扰动输入。对于图1中的常规串级控制来说，无论取消其主回路还是副回路，由于MPC控制器的存在，仍然相当于串级控制。 鉴于以上分析，笔者考虑改变常规串级控制的结构，达到减少串级回路数量的目的。

以化工过程中普遍存在的MIMO串级控制系统为例， 该MIMO控制系统通常由多个单入单出（Single In Single Out，SISO） 串级控制系统通过输出耦合而成，SISO串级控制结构如图1虚线框部分所示。 由于在化工过程中，工艺装置内发生的复杂的化学、 物理反应以及各类扰动均与流量息息相关，所以在该串级控制系统中，副回路通常输出流量被控变量，实现对工艺装置内温度、成分、液位及浓度等主被控变量的输出控制。

值得注意的是， 虽然在化工过程控制中，可以通过串联的主、副控制器使工艺装置作为串级被控对象稳定运行，但是稳态情况下，被控装置中各变量之间的传递函数无从得知。 因此，可以在传统MIMO串级控制系统架构下， 对主回路设定值θsp增加阶跃输入， 以方便地获得MIMO串级回路中各变量q、θ、C的阶跃响应输出数据， 进而通过系统辨识的方法获得输入输出传递函数矩阵H1（s）、H2（s）、H3（s），消除θsp，即可得到被控装置内各变量之间的传递函数矩阵：

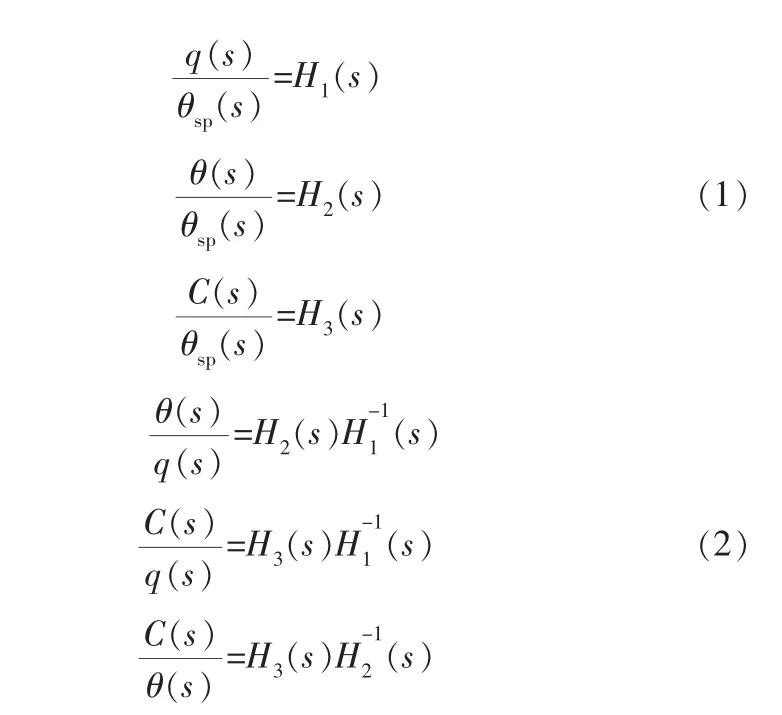
在MIMO控制系统中， 当输入输出维数相同时为方系统，不相同时为非方系统。 本研究中的MIMO系统均为方系统，维数为n。 在方系统的传递函数矩阵中，主对角线位置的传递函数分别表示每一路输入对应每一路输出的传递函数。 例如在式（2）中的传递函数矩阵H2（s）H（s）中，第1个主对角线元素位置的传递函数表示第1路串级回路中流量q到温度θ的传递函数Gp2（s）。 因此，根据主对角线位置的传递函数，即可忽略变量的输出耦合，得到每一路SISO串级结构中各被控变量之间的传递函数，即图1中的Gp1（s）、Gp2（s）。因此，可以利用式（2）进一步分析，得出在MIMO串级控制中， 每一路SISO串级控制转变为如图2所示SISO单回路控制时的传递函数矩阵。

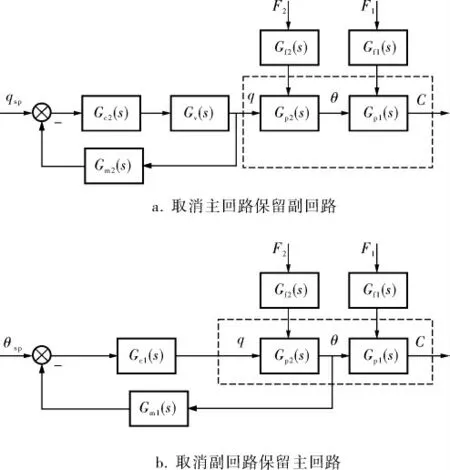
图2 常规串级控制转变为单回路控制

常规MIMO串级控制结构未改变时， 其串级主被控变量设定值θsp对被控变量C的传递函数矩阵为G0（s），由于G0（s）等价于式（1）中的H3（s），因此，将其植入MPC控制器即可完成传统预测控制系统的实现。

为了实现MIMO控制系统每一路SISO串级控制按照图2a所示取消主回路保留副回路时的预测控制系统的设计， 可假设此时MIMO控制系统的传递函数矩阵为G1（s）（式（3））。 由于工业现场无法直接取消主回路，对该单回路控制系统进行系统辨识，因此笔者提出随后的理论推导以获得该传递函数矩阵。 由于图2a中输入输出传递函数对应于G1（s）的主对角线元素位置的传递函数，因此可以利用式（4），由G0（s）得到G1（s）的主对角线元素位置的传递函数，非主对角线元素位置的传递函数可以利用输出相互耦合作用具体分析得知，进而得到取消主回路结构的传递函数矩阵G1（s），式（4）中的参数i（i∈N+）表示MIMO串级控制系统中SISO串级回路的序号。将G1（s）植入MPC控制器，即可实现预测控制输出操纵变量由θsp转变为流量优化给定值qsp，将其作为副回路的给定值，最终实现此类预测控制系统。

同理，每一路串级控制回路中，按照图2b所示取消副回路而保留主回路时，上层预测控制输出操纵变量需要重新转变为串级主被控变量θ的给定值θsp。 假设此时MIMO控制系统传递函数矩阵 为G2（s）（式（3）），同 理 可 以 利 用 式（5）得 到G2（s）主对角线元素的传递函数，即图2b中单回路控制结构的传递函数。 式（5）中Gflow（s）为串级副回路的传递函数，将Gm1（s）、Gm2（s）设置为1。 同样利用实际情况中的输出耦合得到非主对角线元素的传递函数，进而得到传递函数矩阵G2（s），将G2（s）植入MPC控制器即可实现预测控制输出操纵变量为温度优化给定值θsp，将其作为主回路给定值，最终实现预测控制系统。

根据以上两类常规MIMO串级控制系统结构发生改变时的分析可知： 在预测控制架构下，无论对常规串级控制结构做出取消副回路还是主回路的改变，皆可按照式（1）～（5）得到预测控制的参考模型并达到输出操纵变量改变的要求。

2 串级CSTR仿真平台的建立

针对第1节的理论分析以及化工领域广泛存在的“流量被控变量-温度主被控变量”的串级控制系统［17～19］，笔者以一类化工领域常见的串联连续搅拌反应釜为被控装置进行仿真［20］，系统结构原理如图3所示。

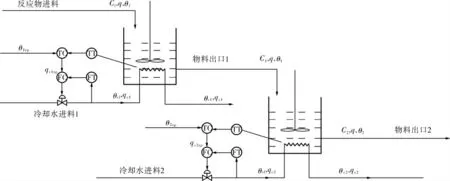
图3 串联CSTR控制结构原理

该CSTR被控装置主要组成为一对串联反应釜、对应冷却水管道与反应物进出料管道，主要目的为通过反应釜内的搅拌作用使进料反应物进行放热反应， 由冷却水流量qc1、qc2分别通过热量交换调节釜内温度θ1、θ2和反应物浓度C1、C2，并且假设两个反应釜内反应物进料与出料流量q均保持一致，使得两个反应釜液位不变，处于理想控制状态。 因此可以在Simulink仿真软件中，通过串级控制实现对串联反应釜的控制，构成双入双出串级CSTR。

物料与能量衡算公式如下：

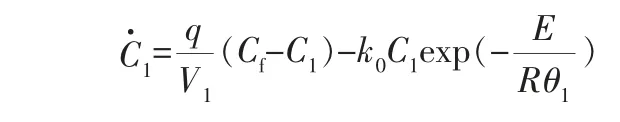
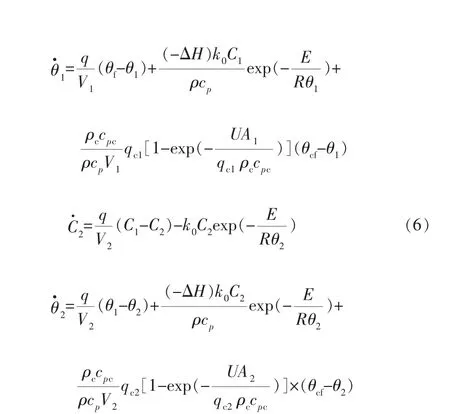
CSTR模型参数见表1。

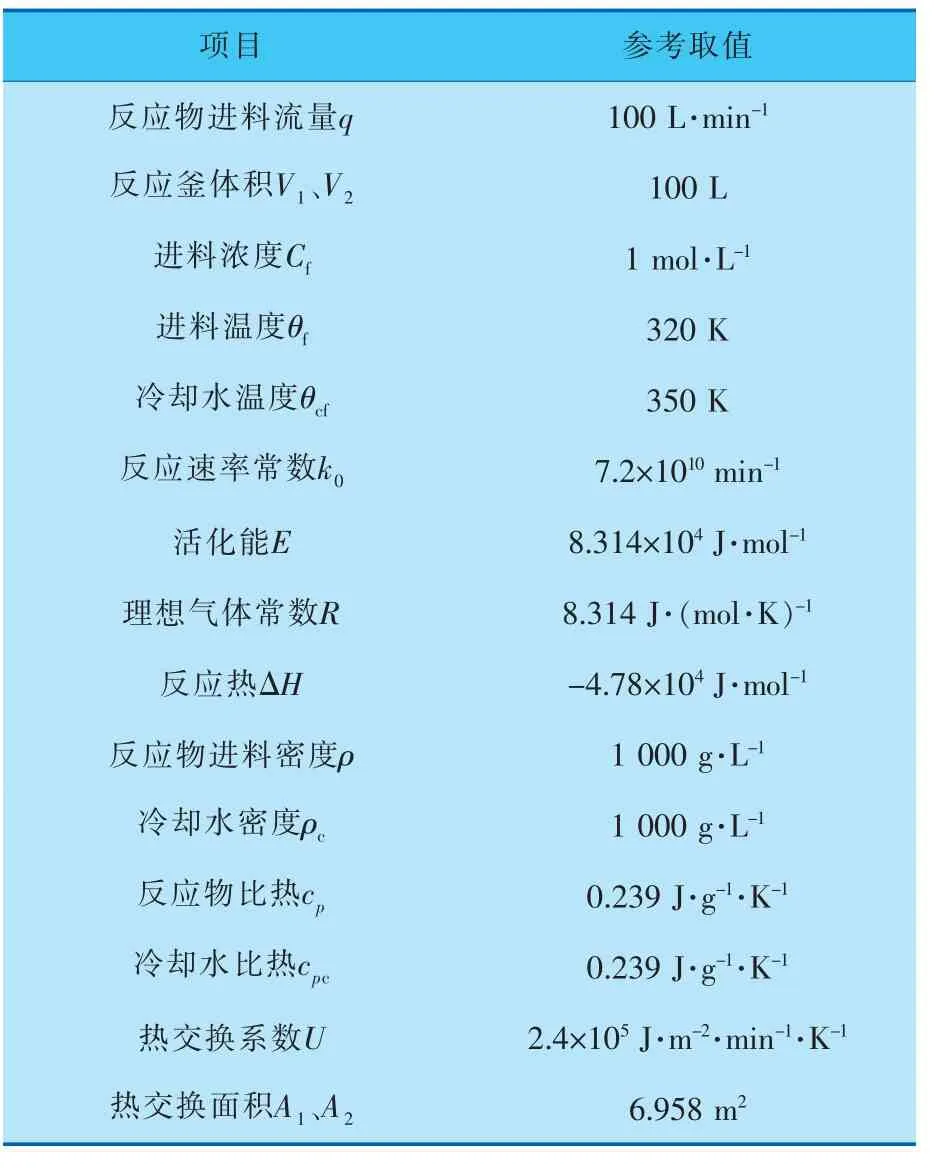
表1 CSTR模型参数

首先通过式（6）和表1中的模型参数，在Simulink软件中编写微分方程，搭建非线性串联CSTR实物模型作为实验被控装置。 其次，分别通过串级控制实现对两个串联反应釜内冷却水流量qc1、qc2和物料温度θ1、θ2的控制，并且串级回路中副回路为流量控制，主回路为温度控制，均采用常规PID控制器。 最终通过调节PID控制器参数，实现对 该 非 线 性CSTR 在 稳 态 点 ［θ1，C1，θ2，C2］=［448，0.06425，428，0.00659］附近的控制，建立双入双出串级CSTR仿真平台。

在添加MPC控制器前，为了以实例验证减少串级回路数量的影响，可以分别取消串级CSTR的主、副回路。 改变3种不同控制结构下的流量设定值qcsp与温度设定值θsp， 分别调节PID控制器参数使最终浓度输出重新达到0.007 00 mol/L并且稳态时间最短，此时PID参数处于最优，动态响应过程如图4所示， 以变化幅度的±1%为允许误差带，计算得出最终稳态时间ts1=3.5 min、ts2=2.5 min、ts3=1.4 min， 因此可以得出相对于传统串级控制，减少串级主、副回路可以使得稳态时间分别减少28.5%、60.0%左右。

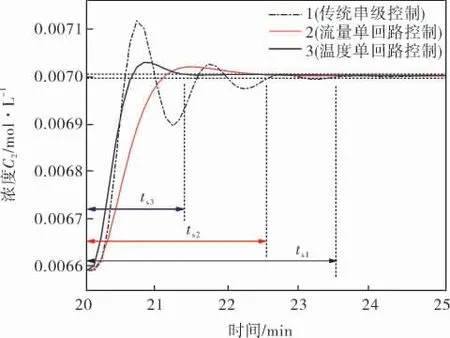
图4 添加MPC控制器前3种不同控制结构下的动态响应

在添加MPC控制器时，首先以传统串级控制结构下的串级CSTR作为预测控制被控对象，预测控 制 系 统 结 构 如 图5 所 示。 在 图5 中，Gqθ（s）、GθC（s）、G′qθ（s）、G′θC（s）分别表示在稳态情况下第1、2个反应釜内冷却水流量qc对产品温度θ、产品温度θ对反应物浓度C之间的传递函数；Gf1（s）、Gf2（s）为第1个反应釜的浓度与温度输出对第2个反应釜的干扰作用；G′m1（s）、G′m2（s）、G′c1（s）、G′c2（s）、G′v（s）为第2条串级回路中相应的传递函数。

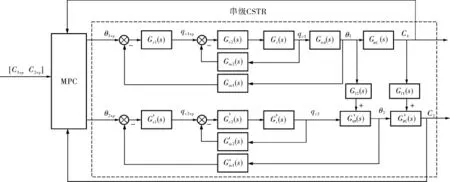
图5 传统预测控制架构下的MIMO串级CSTR被控对象

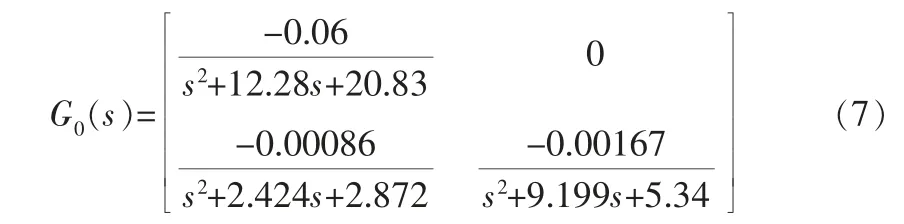
设置MPC 控制器的控制周期t1=ts1/60=0.058 min，保证预测时域长度为ts1/4，因此设置预测步数P=15，控制步数M＝8，仿真得出CSTR装置最终输出反应物浓度C2在传统预测控制架构下的控制效果，结果如图8曲线1所示。其稳态时间ts1变为5 min，因此可以验证添加MPC回路使得串级控制回路复杂度增加、响应时间延长。

为了得到减少回路后的串级CSTR的传递函数矩阵， 可以在串级控制结构下通过阶跃响应测试得到式（1）、（2），将主对角线元素进行传递函数降阶处理后，最终得到每个反应釜内流量qc、温度θ与反应物浓度C三者之间的传递函数（表2）以及Gf1（s）、Gf2（s）。根据G0（s）和表2内的传递函数，可以根据式（3）～（5）对串级被控对象结构进行改变。

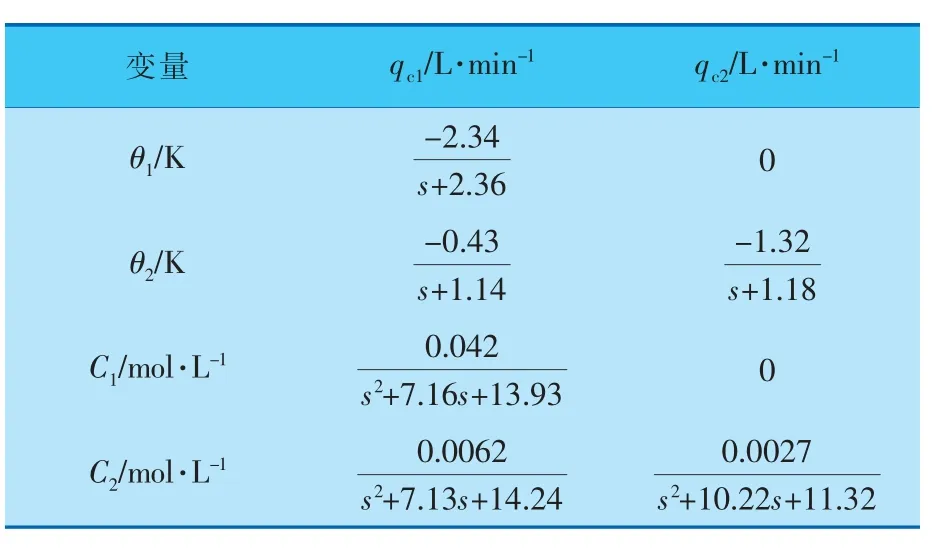
表2 CSTR装置内变量传递函数变量

3 常规控制层只有流量控制器的预测控制设计与实现

传统预测控制架构下，CSTR装置中共有流量qc、 温度θ与浓度C三大类被控变量（Controlled Variable，CV）， 分别纳入串级与预测控制反馈回路。 MPC 控制器输出操纵变量（Manipulated Variable，MV）为温度优化给定值θsp，将其作为常规控制层中温度主回路给定值，通过串级回路实现对不同CV的稳态输出。 但是，由于CV全部纳入反馈， 造成常规控制层存在多层串级的问题，导致装置复杂度增加、 系统响应时间延长等问题。因此根据以上分析，可以减少串级副回路或主回路，以该串联CSTR装置为例进行预测控制系统的设计，观察各类CV的最终控制效果。

笔者首先设计串级控制回路转变为只有流量PID控制器时的流量单回路控制结构， 预测控制系统结构原理如图6所示。

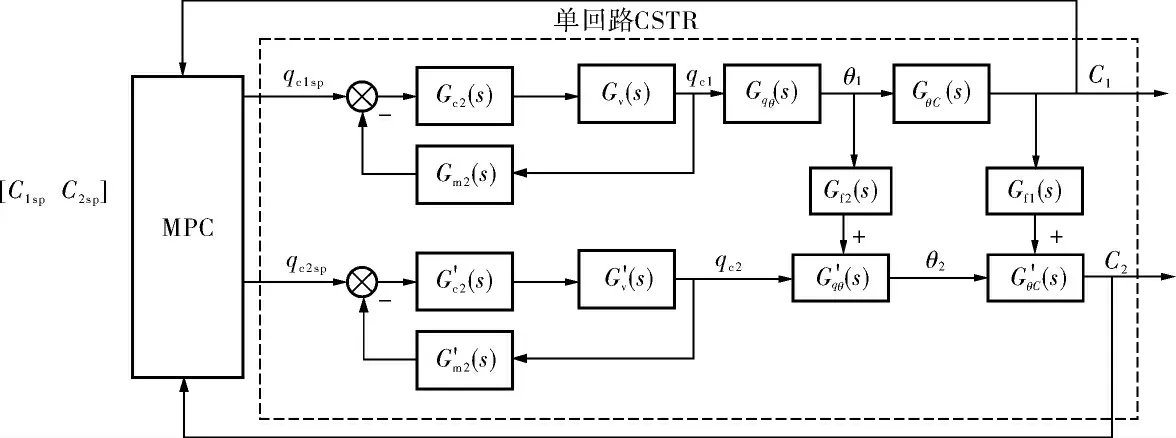
图6 常规控制层只有流量控制器的预测控制原理

此时，MPC控制器的输出MV需要转变为冷却水流量的给定值qcsp，将其作为流量控制回路的给定值， 实现对CSTR装置内冷却水流量的控制，进而控制反应釜内的温度与浓度。 此控制结构相当于利用MPC控制器取代串级控制结构中的全部温度PID控制器， 充分利用了预测控制处理多入多出控制系统的先进性，重新构建了由MPC控制器与PID控制器通过串联组成的串级控制系统，保证了在减少控制回路时系统依然具备串级控制的稳定性。

为实现上述预测控制系统的设计，首先需要对植入MPC控制器的参考模型做出改变，使得预测控制输出对应MV。 根据以上分析，最终由下式得到传递函数矩阵G1（s）：

通过串级CSTR仿真平台，将G1（s）当作参考模型植入MPC控制器，并且设置MPC控制器的控制周期t2=ts2/60=0.042 min，预测时域为ts2/4，因此取预测步数P=15，控制步数M=7，最终得出MPC控制器输出MV为流量优化给定值。 由于减少了温度PID控制器， 此时串级CSTR只保留流量PID控制器，因此在PID参数整定方面更加简单，并且此时原流量副回路同样处于副回路位置，起随动控制作用，因此其PID参数无需调整。

（2）法制建设不健全，法制观念淡薄。尽管我国针对建筑市场的不正之风制定了一系列法律法规，但对一些违法行为缺乏相应的处罚条款，各方主体法制观念淡薄，一些单位和个人仍然知法犯法，有些人根本不学法、不守法，我行我素，胆子很大，没有丝毫规矩和约束，心存侥幸心理，以身试法。

为了观察此时预测控制系统在稳态点附近的控制效果，笔者在20 min系统达到稳态时改变MPC控制器浓度设定值，使浓度从0.006 59 mol/L重新达到0.007 00 mol/L；在30 min时，添加幅值为2%的反应物进料流量正弦波扰动为预测控制可测扰动，观察CSTR内反应物浓度C2的动态响应效果，最终结果如图8中曲线2所示。

4 常规控制层只有温度控制器的预测控制设计与实现

为了达到减少串级回路数量的目的，同样可以设计串级回路转变为只有温度PID控制器的单回路控制结构。

此时MPC控制器与温度PID 控制器串联，CSTR工艺装置内温度与浓度两类CV分别反馈到温度PID控制器与MPC控制器。 因此在结构上分析，在减少结构复杂度的同时，预测控制系统同样具有串级控制的稳定性，系统控制结构原理如图7所示。

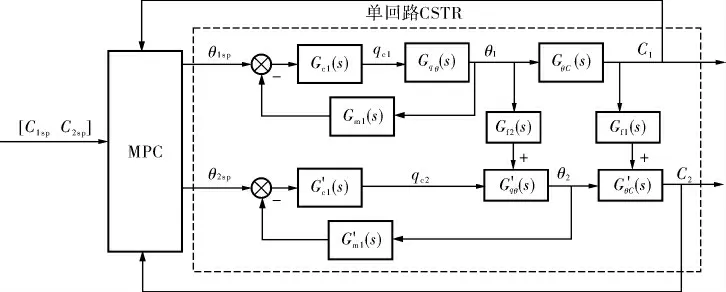
图7 常规控制层只有温度控制器的预测控制原理

MPC控制器输出MV重新转变为温度优化给定值θsp，将其作为温度单回路设定值。温度PID控制器输出控制变量直接作用于CSTR装置内的流量阀，由于流量调节阀可在较短时间内输出响应， 故在取消流量副回路时，其传递函数可忽略不计。

为了在串级CSTR仿真平台实现该预测控制系统的设计，首先需要得到串级CSTR取消副回路后的传递函数矩阵G2（s）。 根据以上分析，最终可由下式得到温度给定值θsp到浓度输出C的传递函数矩阵G2（s）：

其中，Gflow（s）、G′flow（s）分别为第1、2条串级回路中流量副回路闭环传递函数。

在串级CSTR平台中，将G2（s）作为参考模型植入MPC控制器， 同样设置MPC控制器的控制周期t3=ts3/60=0.023 min，预测时域为ts3/4，于是取预测步数P=15，控制步数M=8，此时MPC控制器输出MV重新转变为温度优化给定值θsp，并且作为温度控制回路的给定值， 最终实现对CSTR中各类CV的控制输出。

由第1节分析可知， 此时温度回路由串级主回路转变为预测控制副回路，由定值控制转变为随动控制。 因此需要进一步调整温度PID控制器的参数大小， 即减弱积分作用适当增强比例作用，使温度回路快速反应。

同样， 当该预测控制系统在20 min处于稳态时，改变反应物浓度设定值，使浓度从0.006 59 mol/L重新达到0.007 00 mol/L；在30 min时，添加幅值为2%的反应物进料流量正弦波扰动为预测控制可测扰动，最终控制效果如图8中曲线3所示。

通过综合分析预测控制架构下，传统串级控制与取消串级主回路、 副回路情况下的3条不同控制效果曲线，可以得知，相比于传统情况下的串级控制结构，取消串级中主、副回路可以在预测控制架构下减少系统响应时间。 例如从图8中可以看出，以传统串级CSTR作为MPC被控对象时稳态时间ts1=5.0 min，减少串级回路后的流量单回路控制与温度单回路控制的稳态时间ts2、ts3分别为3.2、3.8 min， 即减少一条串级回路可使得稳态时间分别减少36%、24%左右。 除此之外，在正弦扰动情况下两种单回路控制可以更快速地消除扰动，因此综合得出取消温度主回路效果更佳。

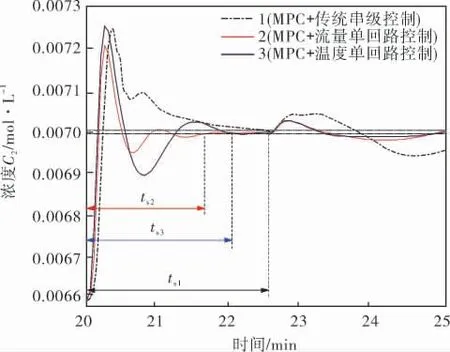
图8 3种不同控制结构下的动态响应

5 结束语

在预测控制架构下，传统串级控制具有响应时间延长与组态复杂的问题，因此可以对常规控制层串级结构做出简化，通过公式给出由串级控制转变为主变量单回路控制、副变量单回路控制时的预测控制器广义被控对象模型。 最后通过搭建串级CSTR控制平台，给出了预测控制系统的具体设计步骤， 以CSTR为实物模型进行了仿真对比。 最终得出串级回路取消温度主回路时效果最好的结论，这样不仅可以减少预测控制系统的稳态调节时间，而且达到了降低串级控制组态复杂度的目的。