基于微分方程的随机网络舆论传播模型研究与分析
周小红
(北京农业职业学院 基础部,北京 102442)
随着网络、大数据、物联网、通信技术[1-2]的不断发展,人们每时每刻都在不停的接收新的信息。丰富的信息获取途径一方面给人们生活带来便利,另一方面也带来了网络中虚假舆论信息大规模传播的隐患[3-5]。虚假舆论信息会对个人、公司企业甚至公共安全产生破坏性影响。因此,亟需准确把握网络中虚假舆论信息传播过程的特点[6],为遏制虚假信息传播提供相应的对策,这已成为应对舆论危机、减少虚假信息传播恶劣影响的重要课题。
为此,大量学者针对舆论传播进行研究,并取得了丰硕成果。徐铭达等[7]基于模体度对社交网络虚假信息传播机制进行了研究,提出了广度模体度与深度模体度的概念来量化传播网络的结构重要指标;张帅[8]运用卡方检验和方差分析揭示社交媒体虚假健康信息的显著特征,并构建了社交媒体虚假健康信息特征清单;张帅等[9]基于统计分析、文本分类和主题挖掘技术,探究了信息疫情下网络虚假信息随时间变化的动态传播特征及演化规律;郭成等[10]提出了一种真假信息传播能力评估的动态规划算法,并对整个网络的信息传播能力进行评估。上述研究中用于描述网络虚假舆论信息传播行为的模型大多是确定性模型,很少有针对传播的随机模型。但在现实世界中,舆论传播模型往往受到环境噪音的影响。特别是在突发事件中,当虚假信息广泛传播时,传播过程受到许多不确定因素的影响,从而增加了传播过程的波动性。
为改善上述问题,本文基于舆论传播模型(spreader ignorant removed,SIR),提出了媒体影响下的网络虚假舆论传播模型非线性动力学模型。首先,将随机白噪声引入非线性动力学传播模型,从而使模型更加真实反应现实情况;其次,对模型进行了数学分析,从而以理论推断舆论传播方式以及系统在平衡点最终状态;最后,运用MATLAB软件进行数值模拟。
1 网络虚假舆论传播模型
经典的SIR可描述为一个[11-12]传染病模型:其中S表示传播者,即接受舆论并传播舆论的节点;I表示无知者,其没有接触舆论,也不会传播舆论,但可能通过接触传播者节点而成为传播者;R表示醒悟者,即在接触舆论后最终决定停止传播舆论的节点。舆论在一定范围内的社区进行传播,令传播总人数为N,则有:
N=S+I+R
(1)
考虑到传播总人数可变,且由于不同类型的个体之间的接触,信息经传输和扩散后,接触个体的类型也可能发生变化。在媒体的影响下,本文对传统SIR模型进行了进一步扩展,建立了网络虚假舆论传播模型非线性动力学模型,具体描述为:
(2)
其中,Λ为迁移率,即个体以一定速率进入给定社区;θ为无知者的免疫力,即在政府干预的影响下,一些无知者θI对虚假信息有自己的判断,即对虚假信息免疫,直接成为醒悟者;β1是无知者与传播者接触、接收和传播舆论的概率,β1IS是指一些无知者选择相信传播者的信息并成为传播者;β2是容易受影响的个体与传播者接触时,传播产生最大影响的概率;β2S/m+S表示当无知者I接触传播者S时,媒体阻止虚假信息传播的概率,随着传播人数的增加,媒体相应地增加报道强度,以防止个人相信和传播虚假信息;当传播人数趋于无穷大时,媒介对传播概率的影响最终达到β2的最大值;m为饱和系数,用来衡量媒体报道对传播的影响;考虑到媒体报道可以减缓虚假信息的传播和扩散,但不能完全阻止其传播,因此假设β1>β2;μ为醒悟率,表征每组个体因某种原因成为醒悟者,从而在接触虚假信息后最终决定停止传播;λ为传播者S遇到醒悟者R,且传播者失去继续传播虚假信息动力的概率。
在虚假舆论传播过程中,相关媒体会根据事件的变化调整报道策略。事件本身是一个随机事件,特别是在紧急事件中,官方媒体的报道可能会受到政府等外部环境因素的影响,因此本文在非线性动力学模型(式(2))的基础上加入随机白噪声,从而使模型更加真实反应现实情况。加入随机白噪声的非线性动力学传播模型可描述如下:
(3)
其中,B1(t)、B2(t)和B3(t)是独立的布朗运动,δ1、δ2和δ3为随机白噪声强度。进一步,可定义以下随机系统:
dX(t)=F(t,X(t))dt+G(t,X(t))dB(t)
(4)
其中,F(t,X(t))为[t0,+∞)∈Rd中定义的函数,G(t,X(t))为d×m维矩阵。此外,F(t,X(t))和G(t,X(t))均为具有一个Lipschitz常数。B(t)为一个m维维纳过程。进一步,令
Sh={x∈Rd:|x| (5) 其中,|x|为欧几里德范式。因此,微分算子可在如下定义的函数上运行 V∈C1,2(R+×Sh;R+) (6) 综上,有 [GT(t,x)Vx(x,t)G(x,t)] (7) dV(t,x(t))=L(t,x(t))dt+Vx(t,x(t))δ(t,x(t))dB(t) (8) (9) (10) (11) 基于微分方程稳定性[13]理论,接下来对模型进行了数学分析。由于该模型描述的网络虚假舆论是以人传人动态过程中传播,因此所涉及的参数均假设为非负值。 引理令网络虚假舆论非线性动力学传播模型的闭集为D,其定义如下: D={(I,S,R3):N≤μ} (12) 则D为正不变集。 证明考虑到传播总人数定义为N=S+I+R,则有 =Λ-μ(S+I+R) =Λ-μN (13) 进一步,有 (14) 当t≥0,有N(0)≤Λ/μ,N(t)≤Λ/μ。在初始条件下,模型的所有解都在闭集D中,因此闭集D是正不变集。 从引理可知,当t趋于无穷大时,N→Λ/μ,为了简化模型的求解,本文考虑网络虚假舆论非线性动力学传播模型的极限系统情况: (15) 令系统的右侧为零,可得到 (16) 因此,有 G(S*)=S*g(S*) =S*(a(S*)2+bS*+c)=0 (17) a=(β1-β2)(λΛ+μ2) (18) b=(mβ1+θ)λΛ-(β1-β2)Λμ+ (mβ1+θ)μ2+μ3 (19) c=m(-β1Λμ+μ3+θ(λΛ+μ2)) (20) 当S*=0时,有I*=Λ/(θ+μ),最终状态为虚假舆论传播者S消失,无知者I趋于常数,则状态方程的平衡点为E(0),则有 (21) 同理,当S*≠0时,则有 (22) 进一步,可根据方程g(S*)=a(S*)2+bS*+c=0计算S*。因此,最后的状态为存在虚假信息传播者S,无知者I趋于常数,该状态方程的平衡点定义为E*,则有 E*=(I*,S*) (23) 因此,根据假设,有β1>β2,故有a>0。此外,当c1≥0,则有-β1Λμ+μ3+θ(λμ+μ2)≥0,令R0为虚假舆论持续和消失的阈值,则有 (24) 参数b可计算如下: m=(mβ1+θ)λΛ-(β1-β2)λμ+ (mβ1+θ)μ2+μ3 (25) 当c<0时,R0>1时,无论b是正的还是负的,g(S*)=0都有唯一的正解。因此,当R0<1时,无论虚假舆论传播的初始状态如何,传播者最终趋于消亡,虚假信息受到良好的控制。相反,如果R0>1,这三个组最终趋于一个稳定值,则虚假信息将持续传播。 令随机白噪声的非线性动力学模型(式(3))中的I(t)、S(t)和R(t)分别表示t时刻无知种群、感染种群和醒悟种群的种群密度。在给定初始值条件下,本节基于李亚普诺夫分析方法对随机白噪声的非线性动力学传播模型是否有唯一的全局解进行分析。 N,I(t)+S(t)+R(t)=N} (26) 进一步,仅需证明τe=∞,从而说明该解为全局解。本文证明了(I(t),S(t),R(t))在有限时间内不会爆发到无穷大。令k0>0足够大,使得(I(0),s(0),r(0))位于区间[1/k0,k0]内。对于每个整数k>k0,停止时间τk可定义如下: τk=inf{t∈[0,τe):I(t)∉(1/k,k)orR(t)∉(1/k,k)} (27) P{τk≤T}≥ε,∀k≥k1 (28) (29) 令X(t)=(I(t),S(t),R(t)),进一步通过使用It公式并计算其期望,可以得到对于所有k≥k0,有 (30) 其中,L1可计算如下: L1 ≤Λ+(a1β1-μ)S+a1(θ+μ)+(b1β1+θ- (31) 令a1=μ/β1,b1=(μ-θ)/β1,则有 (32) 综上,结合式(32)和式(30),有 0≤E(V1(X(TΛτk)))≤V1(X(0))+m0T (33) 令Ωk={τk≤T},对于∀k≥k1和P{τk≤T}≥ε,有P{Ωk}≥ε和V1(X(TΛtk))≥0,即 E(V1(X(TΛτk)))=E(1ΩkV1(X(TΛτk)))+ E(1ΩkV1(X(TΛτk)))≥E(1ΩkV1(X(τk))) (34) 其中,1Ωk是函数Ωk的特征函数。对于∀ω≥Ωk,X(τk,ω)=(I(τk,ω),S(τk,ω),R(τk,ω))的某些分量等于1/k或k,因此,有 V1(X(τk,ω))≥A(k) (35) 其中, A(k)=min(f(1,k),f(1,1/k),f(μ/β1,1/k),f(μ/β2,k),f(μ/β2,1/k)) (36) 同时,有f(a1,x)=x-a1-a1log(x/a1)。 结合式(33)—(35),有 V1(I(0),S(0))≥E(1ΩkV1(S(TΛτk)),I(TΛτk))≥ A(k)P(Ωk)≥A(k) (37) 将k扩展至∞,有 ∞>V1(I(0),S(0),R(0))+m0T=∞ (38) 式(38)矛盾,故必须有τe=∞。因此,可得出结论I(t)、S(t)和R(t)为正解且为全局解。证毕。 为验证所提模型准确性及有效性,本节基于MATLAB 2019A对模型进行数值模拟。设置两组试验,分别对网络虚假舆论传播模型非线性动力学模型(式(2))和随机白噪声非线性动力学传播模型(式(3))进行验证。仿真时选择时间步长Δ=10-3,两组试验涉及的相关参数如表1所示。 表1 数值模型时相关参数Tab.1 Relevant parameters of numerical model 图1 试验1中确定模型和白噪声模型数值模拟结果Fig.1 Numerical simulation results of determined model and white noise model in test 1 根据公式(24),试验1中R0=0.197 1<1。图1所示为试验1条件下确定模型(网络虚假舆论传播模型非线性动力学模型(式(2)))和白噪声模型(随机白噪声非线性动力学传播模型(式(3)))数值模拟结果。其中,横轴分别表示系统仿真时间,纵轴分别为为无知者I、传播者S和醒悟者R的人数。可以看出,虚假舆论传播的规模逐渐减小,直到最终趋于消亡(S=0),这意味着舆论将得到控制。此外,确定模型曲线较为平滑,白噪声模型波动明显,且确定模型曲线均沿着白噪声模型曲线波动。 图2 试验2中确定模型和白噪声模型数值模拟结果Fig.2 Numerical simulation results of determined model and white noise model in test 2 同理,根据公式(24),试验2中R0=1.75>1。图2所示为试验2条件下确定模型(网络虚假舆论传播模型非线性动力学模型(式(2)))和白噪声模型(随机白噪声非线性动力学传播模型(式(3)))数值模拟结果。其中,横轴分别表示系统仿真时间,纵轴分别为为无知者I、传播者S和醒悟者R的人数。可以看出,系统最终状态为三组人数总数趋于一个恒定的值,并在系统中共存,此时仍然存在虚假舆论。一旦外部条件发生变化,系统平衡打破,舆论将继续传播。同理,确定模型曲线较为平滑,白噪声模型波动明显,且确定模型曲线均沿着白噪声模型曲线波动。 综上,模型数值模拟情况与引理(正不变集分析)以及定理(正解存在唯一性分析)理论分析结果一致。因此,数值模拟结果进一步验证了所提模型的有效性。 本文基于SIR传染病模型对网络虚假舆论传播进行了研究与分析,建立了一种确定型的网络虚假舆论传播模型非线性动力学模型和随机的白噪声非线性动力学传播模型。基于微分方程稳定性理论,分别对确定型和随机性模型进行了数学分析,从而确定舆论传播方式以及系统在平衡点最终状态。该模型为政府或新闻媒体部门分析网络中虚假舆论传播以及舆论引导提供了一定借鉴作用。 本文研究主要集中与舆论中虚假信息传播,然而舆论除包含负面因素,还存在正向舆论信息。未来可对舆论中正面信息传播研究,从而积极引导舆论导向。2 数学分析
2.1 正不变集分析
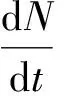

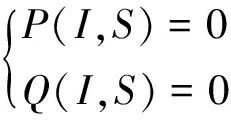
2.2 正解存在唯一性分析

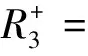


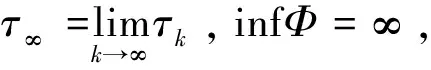



3 数值模拟分析



4 结论

