Hardy空间上的Volterra型积分算子
胡 蓉
(1.四川文理学院 数学学院,四川 达州 635000;2.武汉大学 数学与统计学院,湖北 武汉 430072)
Volterra型积分算子在各类全纯函数空间上的有界性和紧性问题一直受到学者们的广泛研究[1-12]。POMMERENKE首先刻画了Jb在单位圆盘上Hardy空间H2上的有界性[1];之后ALEMAN等研究了Jb在单位圆盘上Hardy空间、Bergman空间上的有界性和紧性问题[2-4]。单位球上的相关结论首先是HU在文献[5]中给出Jb在混合范数空间Hp,q(φ)上的有界性和紧性刻画;接着LI等研究了Jb和Ib在单位球上Bergman空间、Bloch空间以及Hardy空间(p=2时)上的有界性和紧性问题[6-8];AVETISYAN等给出了Jb和Ib在单位球上Hardy空间Hp到Hq(0 记Bn为n上的单位球,H(Bn)表示Bn上的全纯函数全体。任意b∈H(Bn),Volterra型积分算子Jb及其伴侣算子Ib定义如下: R(Ibf)(z)=Rf(z)b(z)z∈Bn (1) 定义1设0 的函数构成的全体为Hardy空间,记为Hp。 定义2H∞为H(Bn)中有界函数全体构成的函数空间,且‖f‖H∞=sup{|f(z)|:z∈Bn}。 任意ξ∈Sn,γ>1,容许进近区域(也称为Korányi区域)Γγ(ξ)定义为: (2) 下面定理为著名的Calderón面积定理,原始定理见文献[5,13],后文将用到的以下版本见文献[10]。 定理A 任意0 容许极大函数及其有界性结论如下[14]: 任意γ>1,f在Bn上连续,Sn上的容许极大函数Mγf定义为 定理B任意0 ‖M(f)‖L p(Sn)≤C‖f‖H p 对Bn中点列{ak},若存在δ>0,使得任意不同两点间的Bergman度量β(ai,aj)≥δ,则称{ak}是可分的。关于单位球中δ-格的性质[14]:任意0<δ<1,存在正整数N,可找到Bn中点列{ak}满足,(a)同Bn=∪kD(ak,δ);(b)集合D(ak,δ/4)两两互不相交;(c)Bn中的任意点z至多包含在N个集合D(ak,4δ)中。我们称满足上述性质的点列{ak}为δ-格。 令φk(t)为Rademacher函数[15]。著名的Khinchine不等式[15]和Kahane不等式[15]如下: 定理C0 定理DX为Banach空间,0 的c={ck}所构成。因为任意两个不同γ对应的Γγ(ξ)所生成的Tent空间在等价的拟范数下相同,故我们在Tent范数中将不同γ对应的Γγ(ξ)均表示为Γ(ξ)。 下面是关于序列Tent空间的对偶性[11]和分解定理[11]: 作为本文的主要结论,下面我们将给出Volterra型积分算子Ib的有界性和紧性的等价刻画。首先给出算子Ib有界和紧的必要条件。 引理1设0 (a)若Ib:Hp→Hq为有界算子,则 (b)若Ib:Hp→Hq为紧算子,则 证明任意z∈Bn,令函数 显然,‖fz‖H p=1,且在Bn的任意紧子集上当|z|→1时fz一致收敛到0。根据Hardy空间上径向导数的增长估计以及(1)式可得: 又因为 从而 结论(a)得证。再根据|z|→1时fz的一致收敛性可证得结论(b)成立。 定理1设0 (a)算子Ib:Hp→Hp有界当且仅当b∈H∞,且 ‖Ib‖H p→H p≈‖b‖H∞ (b)若0 (c)若0 证明(a)必要性由引理1以及最大模原理可得,且有 下面证明充分性。由定理A及(1)式可得: 即有‖Ib‖H p→H p≤C‖b‖H∞,从而根据b∈H∞可得Ib有界。 (c)0 其中 代入Ft的表达式,并对t从0到1积分,再结合Fubini定理,可得 利用定理D,并结合Fubini定理,可得 再利用定理C,可得 (3) 取任意 由(2)式及Hölder不等式可得 再结合(3)式可得 对μk所有可能的分解取下确定,并利用序列Tent空间的对偶性有 等价于 又因为Tent空间不依赖于区域Γγ(ξ)所对应γ的选取,故由上式可得 再根据参考文献[11]中引理3,有 定理2设0 证明充分性显然成立,故只需证必要性。 当0 当0 (4) 设{φk(t)}为Rademacher函数列,在(4)式中用{λkφk(t)}替换{λk},并利用定理1中同样的证明方法,可得 ≤Cεq 根据ε的任意性,可得 这意味着b=0。定理得证。 本文借助调和分析中的面积法和序列Tent空间的分解,给出对所有指标01 基本定义
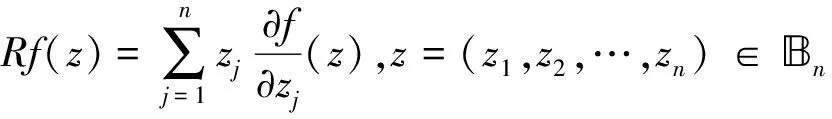

2 预备知识
2.1 面积定理及容许极大函数
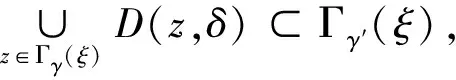
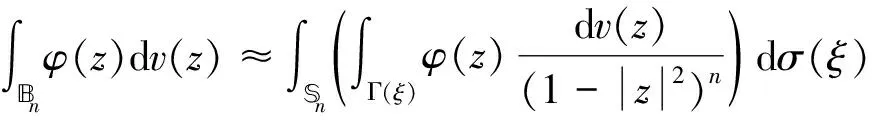
2.2 可分序列和格
2.3 Khinchine和Kahane不等式
2.4 序列Tent空间
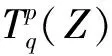
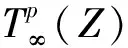
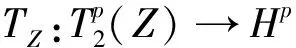
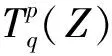
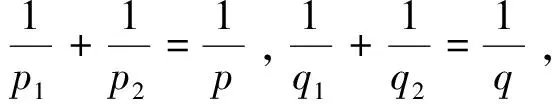
3 主要结果及证明
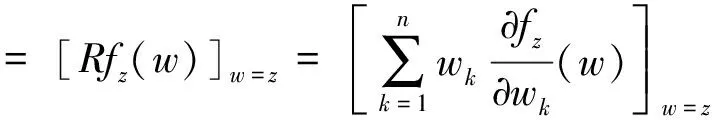
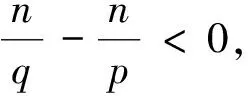
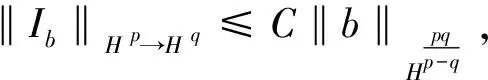
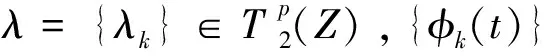
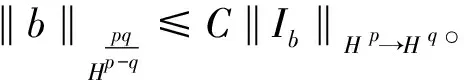
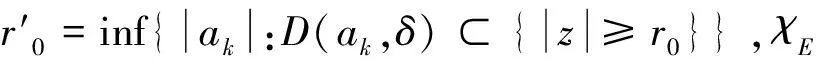
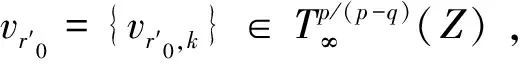
4 结语

